计算机辅助下的露天矿山最终境界简易优化方法
杨 彪
(长沙有色冶金设计研究院有限公司,湖南 长沙 410083)
0 前 言
最终境界是露天矿山开采方案研究的基础,主要的境界优化圈定方法有手工法、L-G 图论法、动锥法、动态规划法、网络流法、储量参数化法以及境界动态优化等方法[1]。传统的手工法是基于矿床平均品位下的二维优化,需根据地质勘探剖面及分层台阶矿体进行多方案的比较分析,工作量大且准确度不高[2]。除手工法外的其余各类优化方法均是基于计算机辅助的境界优化方法,但各方法均需具有一定的优化基础,比如L-G 法、动锥法、动态优化等较为流行的优化方法都需要具备已赋品位、密度等参数的矿床地质块体模型、地表模型等基础模型,还需掌握足够详细的矿石售价、各类成本及境界的几何约束参数[3]。对于很多处于初期开采方案规划研究阶段的矿山项目,在往往面临勘探程度不高、勘探信息不完整等现实问题,无法实现采用地质统计学原理构建矿床品位模型,在露天境界圈定时基本仍采用耗时费力且精度低的手工方法,针对于此,本文提出了一种计算机辅助下的露天矿山最终境界的简易优化方法。
计算机辅助下的最终境界简易优化方法是通过对传统手工法和计算机优化方法充分研究分析的基础上提出的,首先该方法与传统手工法一样,是建立在矿床平均品位下的优化方法;其次,该方法具有与手工法同样的境界确定原则,即境界剥采比小于或等于经济合理剥采比;此外,它充分利用了计算机的快速运算功能,实现了计算机辅助下的境界优化。最终境界简易优化方法的实现可分为矿体实体建模、地表模型创建、块体模型创建、境界优化参数收集和境界优化分析等五步,需要的基础资料包括勘探线平面图、勘探线剖面图、地形等高线、矿床平均品位及矿岩密度、矿山各类经济参数及境界边坡角等。该方法的鲜明特点是基于平均矿床品位模型下的三维快速优化,可实现多方案的快速比较分析,便于矿岩量统计,优化结果可直接用于矿山规划设计的出图,具有方便、快捷、直观、可靠等优点,为露天矿山初期的开采规划提供了一种非常实用的境界圈定方法。
1 优化原理及实现步骤
1.1 优化原理
露天矿山最终境界的确定不仅受到矿石售价、各类成本、几何约束等基本参数的约束,还受到矿体形态及品位分布特征、矿山地形、矿区总图规划及开拓系统、排产规划等因素制约[4],但对于具有一系列批量的境界方案其中必定存在一个最优的境界方案,这个最优方案就是境界优化过程中需要寻找的最终境界。如图1 所示的由小至大的pit1、pit2、pit3……一系列境界方案中必定存在一个最好的境界方案。

图1 系列境界方案示意图
图2 所示为某矿体一剖面上的境界范围图,ABCD 为矿体境界范围,取矿体上盘稳定边帮角为δ,下盘稳定边帮角为β,矿石回收率为η。如果境界深度增加△H,境界变为A'B'C'D',此时境界内岩石增加量为△W,矿石增加量△O,则该部分增加的岩石量与矿石量之比称为“境界剥采比”,计算方法见公式1。

经济合理剥采比(ne)是露天开采境界的经济依据,确定经济合理剥采比的方法较多,归纳起来可分为两类,即比较法和价格法[5]。比较法是以露天开采和地下开采的经济效果作为比较来计算的,用以划分矿床露天开采和地下开采的界线,价格法是用露天开采成本和矿石价格作比较来计算的,在矿床只宜露天开采的场合,用以划分矿床露天开采部分和暂不宜开采部分的界线。通过比较境界剥采比与经济合理剥采比的关系,在满足公式2 时可确定此时的境界即为最终境界。

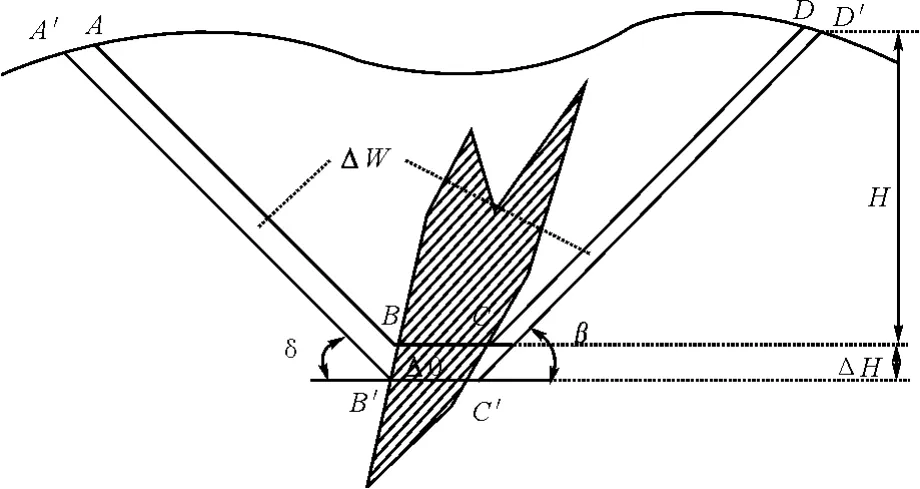
图2 境界剥采比示意图
1.2 实施步骤
计算机辅助的境界简易优化方法的实现主要包括矿体实体建模、地表模型创建、块体模型创建、境界优化参数收集和境界优化分析等5 个步骤,其中矿体实体建模、地表模型创建、块体模型创建三步可称为基础模型创建阶段,后面两步可概括为优化分析阶段。图3 所示为简易优化方法的流程图。
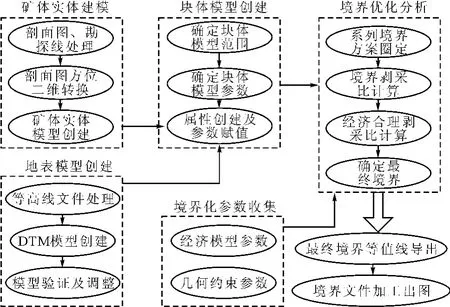
图3 简易优化方法实施流程图
矿体实体建模主要包括基础资料前处理、图形转换、矿体实体生成及检验等内容。首先对地质剖面图清理,如坐标系统调整、轮廓线的提取等,然后将剖面图在三维空间里转换至实际坐标系统,按照前面步骤逐个将地质剖面处理后便可连接形成矿体实体,检验通过的实体模型可用于各类计算或创建约束文件。地表模型创建则相对较为简单,首先整理等高线,将地形移至统一的坐标系统,对等高线高程赋值,检查等高线之间的交叉点、聚结点并生成三维面文件,对形成的面文件进行验证。块体模型创建时首先要根据勘探线平面图、矿体分布等信息确定块体模型的三维空间范围,然后根据台阶高度和矿体特征确定单个块体尺寸,最后创建块体模型的基本属性,主要包括品位、密度、矿岩类型等,采用实体文件、面文件及其他约束手段对块体属性进行赋值[6]。
境界优化参数收集主要包括经济参数和几何约束参数两大类。其中经济参数主要有矿石中各有用元素的价值、矿岩采剥成本、选矿成本、运输成本、各种管理费用及采选回收率等,几何约束包括各方向的最终境界边坡角、空间上的范围限制等[7]。在拥有矿床基础模型和各类参数的基础上便可进行矿山境界的粗圈,通过采用售价、成本折扣或其他约束手段可获得一系列的开采境界方案,利用公式(1)计算各方案之间的境界剥采比,并将其与矿山经济合理剥采比对分析,进而确定最终境界。将确定的最终境界文件导出,可进行后续的排产规划、加工出图等工作。
2 应用实例
2.1 矿山概况
某矿为一中型、矽卡岩铅锌银多金属矿床,矿床Pb 平均品位2.77%,Zn 平均品位3.04%,Ag 平均含量36.06 g/t。矿体为两个近似平行的急倾斜中厚至厚大矿体,矿体厚度在3.12 ~24.6 m,矿体上部露头,往深部延伸约500 m。矿床水文地质条件、工程地质简单,环境地质条件良好。根据矿床赋存特征及开采环境分析,该矿宜采用浅部矿体露天开采、深部资源地下回采的露天+ 地下的开采方式。矿床采用钻探、槽探及坑探等多种勘探方式,钻孔数据不完整且缺少详细的取样点坐标数据,故该矿山在前期开采方案规划研究阶段较适合采用本文提出的境界简易优化方法。
2.2 基础模型创建
矿山目前拥有的基础资料主要包括矿区地形图、由12 条勘探线控制的地质剖面图、矿床的各有用元素的平均品位。首先根据地形图提取了矿区等高线,在SURPAC 中创建了地表DTM 模型。在地质剖面图中提取矿体轮廓线,并进行坐标系统的空间转换,将各矿体剖面连接形成矿体实体。图4 所示为最终形成的矿山地表模型和矿体实体模型。

图4 地表及矿体实体模型
根据矿体形态及范围确定了矿床块体模型的空间范围,露天矿开采台阶高度取10 m,在考虑到矿体的厚度情况下,最终确定单个块体尺寸为5 m ×5 m×5 m。图5 所示为尚未创建属性的矿床块体模型。

图5 矿床地质块体模型
在矿床块体模型中创建Pb、Zn、Ag 等元素的品位属性和矿岩的密度、岩性等属性,采用矿体实体约束方式进行品位属性赋值,将各元素的平均平均品位信息赋予矿体的块体模型中,利用地表模型和矿体实体模型联合约束进行矿岩的密度、岩性属性赋值。图6 所示是矿体的块体模型,此时块体已具备各类属性。

图6 矿体块体模型
2.3 境界优化分析
结合矿山实际情况并采取类比法收集了矿山的主要境界优化参数,各数据见表1。矿石的开采回收率为0.95%,各元素的选矿回收率均取85%。

表1 主要境界优化参数
利用L-G 法,以5%的售价折扣步距进行境界圈定,获得了-30、-25、-20……等一系列境界坑方案,其中-10 表示此时矿产品售价为原售价的1.1倍,而10 表示此时售价为原售价的0.9 倍。图7 为获得的一系列境界坑的叠加图。
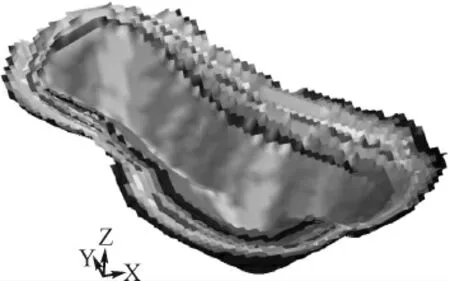
图7 系列境界坑叠加图
统计各境界方案的矿岩量,计算各境界平均剥采比及之间的境界剥采比,统计及计算结果见表2。由表2 可知,随着对矿石售价的折扣,获得的12 个境界方案自上而下境界逐渐变小,所能承担的剥采比也逐渐减小,境界剥采比也随之变小。由于该矿深部存在地下开采可能,故采用比较法计算该矿的经济合理剥采比为8.14 t/t,对比表2 可知,矿石售价折扣为10 时的境界方案对应的境界剥采比为7.81 t/t,小于经济合理剥采比,而其上一境界对应的境界剥采比则大于经济合理剥采比,故选择折扣10 的境界较为合理。

表2 境界间矿岩统计
2.4 优化结果输出
在确定最终境界之后可将境界文件导出,如图8 所示,通过对三维境界坑文件提取以台阶高度为步距的等值线可获得最终境界各台阶的单线条控制线,在此基础上可进行详细的台阶布置和开拓系统规划等工作。
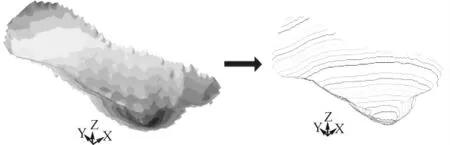
图8 最终优化结果
3 结 语
本文针对部分露天矿山在前期方案规划研究阶段缺乏足够的地质勘探信息的现实问题提出了露天矿境界优化的简易优化方法,并对该方法的实施步骤做了说明,将该方法在某矿山的开采方案规划中进行了实际应用,得出如下结论:
(1)露天矿最终境界简易优化方法能在矿山基础资料匮乏的情况下仍可充分利用计算机的高速运算特性,实现计算机辅助下的矿山最终境界三维优化分析,直观、快捷、易于修改,可在短时间内进行大量方案比较分析,提高了方案的可靠性,优于手工方法。
(2)将该方法在某铅锌银多金属矿山的前期开采方案规划研究中进行了应用,创建了该矿山的基础模型,获得了系列境界方案,通过比较分析获得了矿山的最终境界。实际应用也印证了该方法的优越性。
(3)露天矿最终境界的简易优化方法是建立在矿床平均品位模型下的优化手段,其结果在精度上存在一定的问题,故该法较适用于无法实现详细的地质品位模型赋值时的项目前期方案研究阶段,而并不适用于矿山的详细设计阶段。
[1] 王 青,王智静.露天开采整体优化-理论、模型与算法[M].北京. 冶金工业出版社,2000:1-6,41-42.
[2] 牛成俊.现代露天开采理论与实践[M].北京. 科学出版社,1990:174-178.
[3] 杨 彪,罗周全,廖江南,等.露天矿山开采境界动态优化圈定[J].煤炭学报,2010,35(3):368-372.
[4] Akbari A. D.,Osanloo M.,Shirazi M. A.,Reserve estimation of an open pit mine under price uncertainty by real option approach[J]. Mining Science and Technology,2009,19(6):709-711.
[5] 郭振春. 经济合理剥采比的计算方法和分析[J].现代矿业,2010,498(10):116-118.
[6] 杨 彪.露天矿开采境界动态优化研究及应用[D]. 长沙:中南大学.2011.
[7] 杨 彪,罗周全,陆 广,等.复杂多金属露天矿山最终境界动态综合优化[J].矿冶工程,2011,31(1):1-4.

