侧边加劲带缝钢板剪力墙抗侧刚度及极限承载力计算

陆金钰 范圣刚 闫鲁南 王恒华

(1东南大学混凝土与预应力混凝土教育部重点实验室,南京 210096)

(2东南大学国家预应力工程技术研究中心,南京 210096)

带缝钢板剪力墙是一种新型抗震组件,通过在墙板上开设竖缝来达到调节刚度和承载力、提高变形能力的目的,可仅通过高强螺栓与上下框架梁连接,便于开设门窗,具有布置灵活和安装方便等优点[1-2].经合理设计墙板几何参数及开缝参数,可保证在墙板发生整体失稳前,缝间墙肢端部充分实现塑性屈服,此时带缝钢板剪力墙具有良好的延性和耗能能力.

Hitaka等[1-2]率先进行了一系列带缝钢板剪力墙缩尺试件的单调加载和循环加载试验,研究内容包括开缝参数、加劲肋形式对墙板受力性能的影响及带缝钢板剪力墙与抗弯框架结构的相互作用.随后,Cortés等[3-4]采用试验及有限元分析方法研究了带缝钢板剪力墙与铰接框架的协同工作性能.国内对带缝钢板剪力墙的研究始于2004年,主要采用循环加载试验及有限元仿真分析等方法,对墙板的延性、滞回性能及稳定性能进行研究[5-8].

为方便将带缝钢板剪力墙用于工程设计,合理估算承载力和刚度很有必要.本文提出了一种考虑侧边加劲肋影响的弹塑性承载力估算公式,将估算结果与有限元分析结果进行对比,验证了该估算公式的计算精度.需指出的是,公式适用于能实现屈曲前屈服的剪力墙.

1 带缝钢板剪力墙受力特性

带缝钢板剪力墙由开缝钢板和两侧边缘加劲肋焊接而成,钢板采用激光切割机开缝以减小残余应力和残余变形,为减小应力集中,竖缝端部采用圆弧过渡[1].带缝钢板剪力墙的几何模型如图1所示.图中,h,B,t分别为剪力墙的有效高度、宽度和厚度,l,b分别为缝间墙肢高度和宽度,d,m分别为开缝宽度和层数,r为竖缝端部圆弧半径,n为每层墙肢数量,bs,ts分别为边缘加劲肋宽度和厚度.实际工程中,可通过调整上述参数来满足刚度及承载力的不同要求.本文分析中忽略残余应力影响.

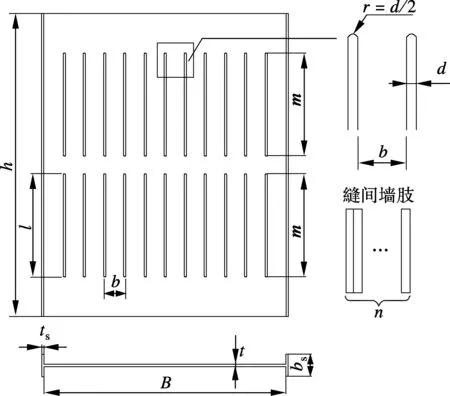
图1 带缝钢板剪力墙的几何模型

不同板幅的带缝钢板剪力墙受力及耗能机理有较大差别,本文主要针对宽高比约为1/2的墙板进行研究.它与宽高比大于等于1的墙板拥有同样的延性和耗能能力,且更易实现屈曲前屈服,在建筑功能上具有更大的灵活性[3,8].

2 抗侧刚度计算

带缝钢板剪力墙承受水平荷载时的变形有如下特点:非开缝板带区因宽高比较小,以剪切变形为主,弯曲变形很小;开缝区域兼有剪切变形和弯曲变形,但以墙肢弯曲变形为主.基于此,文献[1]采用下式估算初始抗侧刚度:

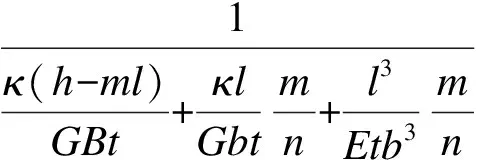
(1)

式中,E为弹性模量;G为剪切模量;κ=1.2为矩形截面的型式因子.

式(1)分母中的第1项表示非开缝板带区域剪切变形,第2项表示开缝区域剪切变形,第3项表示开缝区域弯曲变形.因墙板变形以缝间墙肢的弯曲变形为主,故开缝区域的弯曲变形起决定性作用,它是在假设缝间墙肢两端完全固支的情况下得到的,但实际上非开缝区域对缝间墙肢端部并不能形成完全刚性约束,且墙板在受力时会在竖缝端部产生应力集中,加剧该区域的局部变形,故一般情况下式(1)给出的估算值偏大.

为考虑上述局部变形的影响,文献[9]将墙板开缝区域的弯曲变形乘以修正系数μ,该修正系数通过对文献[1]中的试验数据拟合得到,本质是通过加大缝间墙肢的高度来近似考虑墙肢端部转动的影响.修正系数μ的计算公式为

(2)

一般情况下,竖缝宽度较小,故可用nb近似代替墙板宽度B.将式(2)代入式(1),并假定nb=B,可以得到

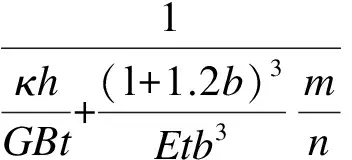
(3)

式(3)分母中的第1项表示单位水平荷载下非开缝板的剪切变形,第2项表示缝间墙肢在单位水平荷载下的弯曲变形.可见水平荷载下带缝钢板剪力墙侧向变形能力比非开缝板强.然而,式(3)并未考虑墙板两侧边缘加劲肋的影响,这是因为文献[1]中的试件墙板整体宽高比均较大(接近1.2),且每排缝间墙肢数较多,边缘加劲肋对整体抗侧刚度的影响不大.但当墙板的宽高比较小(如0.5或更小)时,必须计入边缘加劲肋的影响,否则会造成较大误差[10].

根据试验研究结果可知,带缝钢板剪力墙最外侧墙肢与侧边加劲肋构成的T形截面构件在水平荷载作用下共同抗弯.为考虑侧边加劲肋对剪力墙抗侧刚度的影响,可将最外侧缝间墙肢等效为T形截面.但由于T形截面的剪切型式因子较难求得,且考虑T形墙肢后位于同一开缝层的各墙肢的抗侧刚度不再相等,若采用杆件刚度串、并联的方法进行推导,公式表达将非常复杂,不便于应用.为此,本文在式(3)的基础上,采用简化修正方法来考虑边缘加劲肋影响.因墙板开缝区域的弯曲变形对墙板抗侧刚度起控制作用,故仅考虑边缘加劲肋对开缝区弯曲变形的贡献,并用m/[2kT+(n-2)kR]代替式(3)分母中的第2项,其中,kT为两侧T形截面墙肢仅考虑弯曲变形时的抗侧刚度;kR为墙板中部矩形截面墙肢仅考虑弯曲变形时的抗侧刚度.则式(3)可转化为

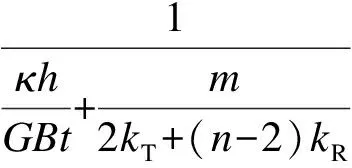
(4)

T形截面和矩形截面墙肢的抗侧刚度计算公式为

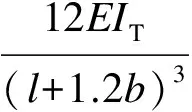
(5a)

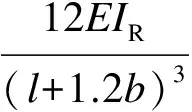
(5b)

式中,IT,IR分别为T形截面和矩形截面墙肢的截面惯性矩.缝间墙肢长度仍取l+1.2b.

3 弹塑性承载力计算

带缝钢板剪力墙以面内受力为主时,各缝间墙肢的受力类似于底端固支、顶端为滑移支座的受弯梁.对于矩形截面的缝间墙肢,端部形成塑性铰时对应的塑性弯矩为

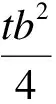
(6)

式中,σy为钢材屈服应力.

作用在墙肢上的剪力为

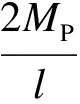
(7)

试验表明,墙板达到塑性屈服承载力时各缝间墙肢均在端部形成塑性铰,故塑性承载力可取各缝间墙肢塑性承载力的代数和[1],即

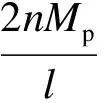
(8)

式中,Qu为弹塑性侧向承载力.

式(8)并未考虑两侧加劲肋的影响,对于实现了屈曲前屈服的带缝钢板剪力墙,往往会低估其承载力[3,5].文献[3]指出,考虑边缘加劲肋影响的塑性承载力公式的计算结果较式(8)的计算结果更接近于试验值，其推导过程与式(8)基本相同,唯一区别在于将最外侧墙肢看作T形截面以计入边缘加劲肋影响,且假设墙板达到塑性承载力时,T形截面墙肢的端部也形成塑性铰.当边缘加劲肋厚度与墙板厚度相同时,弹塑性侧向承载力可表示为

(9)

4 有限元分析

为验证式(4)和(9)的计算精度,采用通用有限元程序ANSYS对18个开缝参数不同的带缝钢板剪力墙进行了弹塑性Pushover有限元分析,将有限元分析结果与公式计算结果进行比较.

4.1 有限元模型

在带缝钢板剪力墙模型中,选用四节点塑性有限应变壳单元(Shell181)来模拟墙面板和加劲肋,采用映射网格划分,对缝端应力集中区域进行网格加密,同时考虑了材料非线性和几何非线性.钢材本构考虑理想弹塑性模型和三折线模型2种情况,选用Q235B钢材,弹性模量E=2.06×105N/mm2,屈服应力σy=235 N/mm2;对于三折线本构模型,屈服后切线模量Et=0.01E,极限强度σu=375 N/mm2.材料采用Von Mises屈服准则和等向强化模型.模型边界条件见文献[11].采用一致缺陷模态法对墙板施加初始几何缺陷,选用第一阶屈曲模态作为初始缺陷的波形,幅值取剪力墙长边尺寸的1/1 000[10].

4.2 结果对比

所采用的剪力墙具有如下几何参数:有效高度h=3 000 mm,高厚比h/t=200,宽高比B/h=0.5,加劲肋厚度ts与板厚t相同.采用的参数与实际应用的墙板参数接近,且满足墙板经济性和受力合理的要求[10].

表1为分析模型的几何参数.所取的开缝参数可保证带缝钢板剪力墙在3.5%侧移角内不出现明显的强度下降(即承载力不低于极限承载力的0.85倍),且均基本实现塑性屈服[10].因表中模型在规范限定的弹塑性侧移角(即2%)内均未出现承载力下降现象,故本文对表中模型取2%侧移角时的承载力为极限承载力.

表2列出了各带缝钢板剪力墙的极限承载力和初始刚度.通过对比表中第2列～第4列数据可以发现,对于b/h较小且l/h较大的剪力墙,式(9)的计算结果与有限元分析结果吻合良好,表明该公式具有一定的合理性.由表中e1可发现,随b/h的增大或l/h的减小,式(9)的计算误差增大,计算值明显高于有限元分析结果.随开缝参数b/h的增大或l/h的减小,剪力墙在相同侧移角下的面外变形越明显,虽然对于经合理开缝参数设计的墙板,这种面外变形不足以导致面外失稳破坏的发生,但对墙板的极限承载力会造成不容忽视的影响,导致式(9)计算误差增大.由表中e2可见,考虑材料强化后,式(9)给出了偏于保守的估算结果,仅对个别b/h和m均较大的情况,计算值略大于有限元结果.

图2给出了墙板加载全过程下的承载力-侧移角曲线.由图可知,随开缝参数b/h的增大或l/h的减小,剪力墙面外变形的幅值明显增大,相应的承载力-侧移角曲线与理论曲线的差距也迅速变大.

面外变形的出现会导致墙板实际承载力较式(9)的计算值偏小,故可乘以折减系数0.9来考虑面外变形的影响.由表2中折减结果可以看出,对于实现了屈曲前屈服的墙板,折减后的极限承载力为较合理的估算值,且结果偏于保守.

由表2中e3，e4可知,式(3)明显低估了剪力墙的初始刚度,而考虑加劲肋影响的式(4)的计算结果则与有限元分析结果吻合较好,误差均在3.5%以内,这表明了在计算抗侧刚度时考虑加劲肋增强效应的必要性.

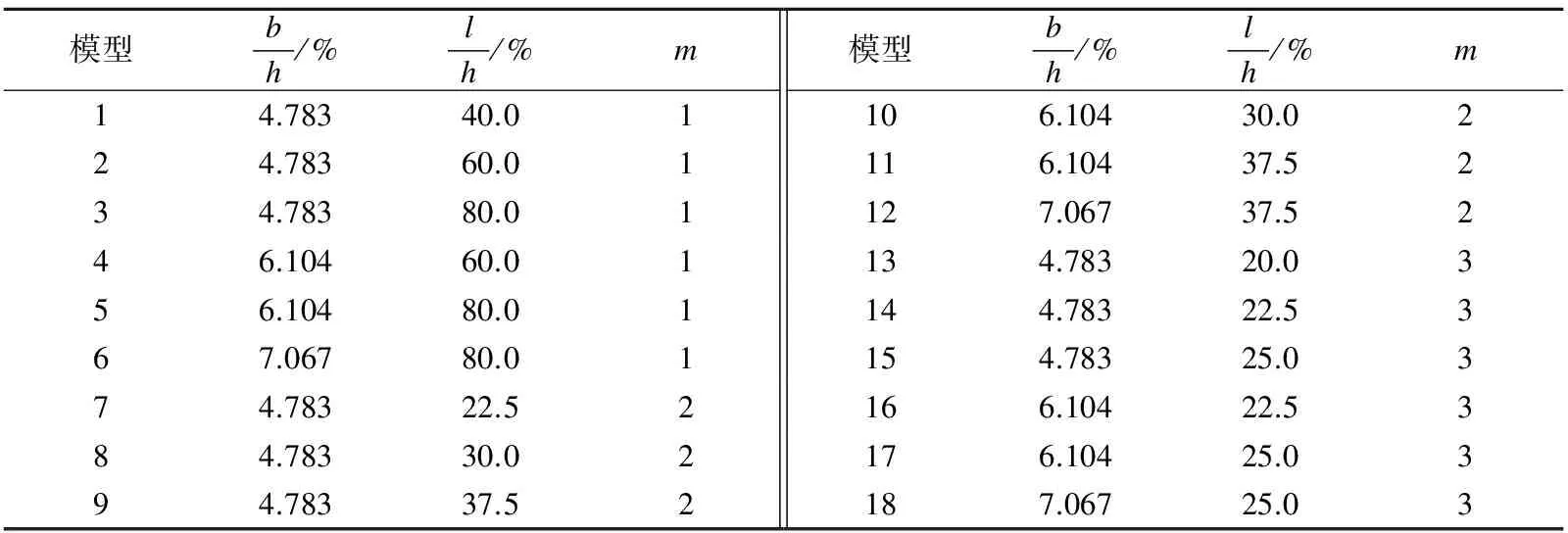
表1 各模型的几何参数

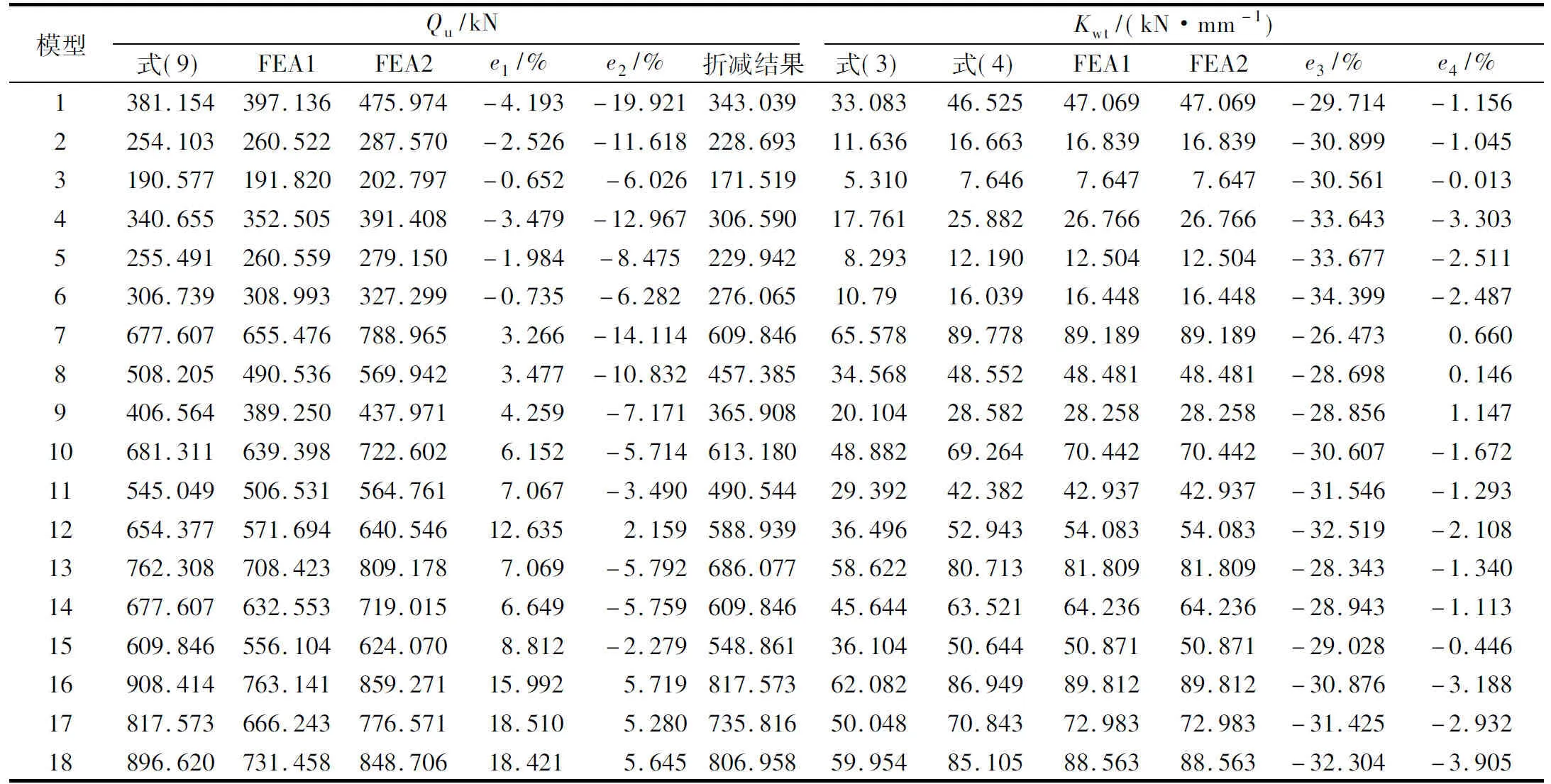
表2 带缝钢板剪力墙的极限承载力和初始刚度

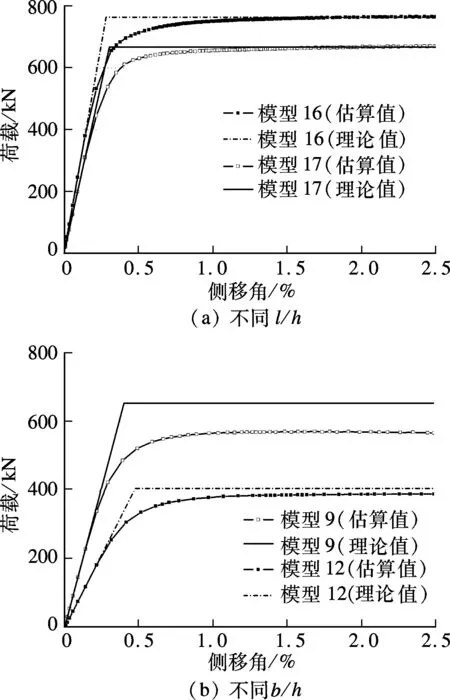
图2 带缝钢板剪力墙的承载力-侧移角曲线

5 结论

1) 考虑了边缘加劲肋对带缝钢板剪力墙开缝区域弯曲变形的影响后,墙板抗侧刚度计算公式的精度大大提高,与有限元计算结果的误差可控制在3.5%以内.

2) 随开缝参数b/h的增大和l/h的减小,墙板面外变形对带缝钢板剪力墙极限承载力的影响越来越明显,导致完全按面内变形推导的估算公式偏于不安全.数据对比结果显示,乘以折减系数0.9后的极限承载力计算值较合理且偏于安全.

3) 本文提出的抗侧刚度及极限承载力计算公式适用于实现屈曲前屈服的带缝钢板剪力墙.

)

[1]Hitaka T,Matsui C.Experimental study on steel shear wall with slits [J].JournalofStructuralEngineering,ASCE,2003,129(5): 586-595.

[2]Hitaka T,Matsui C,Sakai J.Cyclic tests on steel and concrete-filled tube frames with slit walls [J].EarthquakeEngineeringandStructuralDynamics,2007,36(6): 707-727.

[3]Cortés G,Liu J.Experimental evaluation of steel slit panel-frames for seismic resistance [J].JournalofConstructionSteelResearch,2010,67(2): 181-191.

[4]Cortés G,Liu J.Analytical investigation of steel slit panels for lateral resistance of steel frame buildings [C]//Proceedingsof2008ASCEStructureCongress.Vancouver,Canada,2008: 1-5.

[5]赵作周,肖明,钱稼如,等.开缝钢板墙抗震性能的试验研究 [J].建筑结构,2007,37(12): 105-109.

Zhao Zuozhou,Xiao Ming,Qian Jiaru,et al.Experimental study on seismic behavior of steel plate shear walls with vertical slits[J].BuildingStructure,2007,37(12): 105-109.(in Chinese)

[6]曹春华,郝际平,王迎春,等.开缝薄钢板剪力墙低周反复荷载试验研究 [J].西安建筑科技大学学报:自然科学版,2008,40(1): 46-52.

Cao Chunhua,Hao Jiping,Wang Yingchun,et al.Cyclic test of thin steel plate shear wall with slits [J].JournalofXi’anUniversityofArchitecture&Technology:NaturalScienceEdition,2008,40(1): 46-52.(in Chinese)

[7]曹志亮.带缝钢板剪力墙稳定性分析 [D].武汉: 武汉理工大学土木工程与建筑学院,2004.

[8]闫鲁南,陆金钰,王恒华.带缝钢板剪力墙弹性屈曲性能研究 [C]//第20届全国结构工程学术会议.宁波,中国,2011: 401-408.

Yan Lunan,Lu Jinyu,Wang Henghua.Elastic buckling behavior of steel plate shear wall with slits[C]//The20thNationalConferenceonStructuralEngineering.Ningbo,China,2011: 401-408.(in Chinese)

[9]蒋路,陈以一.带缝钢板剪力墙弹性抗侧刚度及简化模型研究 [J].建筑科学与工程学报,2010,27(3): 115-120.

Jiang Lu,Chen Yiyi.Research on elastic lateral stiffness and simplified model of steel plate shear wall with slits [J].JournalofArchitectureandCivilEngineering,2010,27(3): 115-120.(in Chinese)

[10]闫鲁南.带缝钢板剪力墙稳定性能及滞回性能研究[D].南京: 东南大学土木工程学院,2011.

[11]陆金钰,王恒华,闫鲁南,等.带缝钢板剪力墙滞回性能研究 [J].工程力学,2013,30(3): 214-223.

Lu Jinyu,Wang Henghua,Yan Lunan,et al.Hysteretic behavior of stiffened steel plate shear wall with slits [J].EngineeringMechanics,2013,30(3): 214-223.(in Chinese)