一种共用定位销的多工序夹具布局优化设计准则

张 磊 张志胜 周一帆 戴 敏 史金飞

(1东南大学机械工程学院,南京 211189)

(2徐州工程学院机电工程学院,徐州 221018)

在复杂产品的多工序装配过程中,夹具系统定位元件的布局对保证产品的装配质量至关重要．而在进行夹具布局的最优设计时,其设计准则直接影响到装配的效率和精度．

一个夹具系统布局设计的准则主要依据对夹具系统的功能要求．一些学者将定位精度作为夹具首要的功能要求[1-3]．另外,夹持稳定性也是进行夹具布局设计需要考虑的方面,即确定加持力的大小和夹持位置以使工件在工作载荷下变形最小[4-6]．

然而,上述夹具布局优化设计准则仅局限于单工序,对多工序而言,由于缺少能够描述多工序偏差传递和累积的数学模型,夹具布局优化设计问题鲜有文献涉及．Jin等[7]使用状态空间方法首次建立了用于描述多工序装配过程偏差传递和累积的状态空间模型．由该模型提取出的夹具布局设计准则被Kim等[8-11]用于多工序夹具布局设计．

本文将针对一种共用定位销的多工序装配夹具系统的布局问题,改进状态空间方程,提出新的夹具布局设计准则．使用新准则进行多工序装配夹具系统布局设计,结果表明该准则与Kim等[8]所提出的传统准则相比同样有效,且设计效率更高．

1 共用定位销的多工序装配过程表达

共用定位销的多工序装配夹具系统是指在复杂零件的装配过程中,不同工序所使用的装配夹具均共用同一定位销．如图1所示,某车辆侧板装配过程由4个零件经4道工序完成:工序Ⅰ进行A柱和B柱的装配;工序Ⅱ将A柱和B柱所组成的装配部件与顶部侧板装配;工序Ⅲ将工序Ⅱ完成的装配部件再与后围侧板装配;工序Ⅳ进行装配体上关键产品特征(KPC)M1～M10的检测．

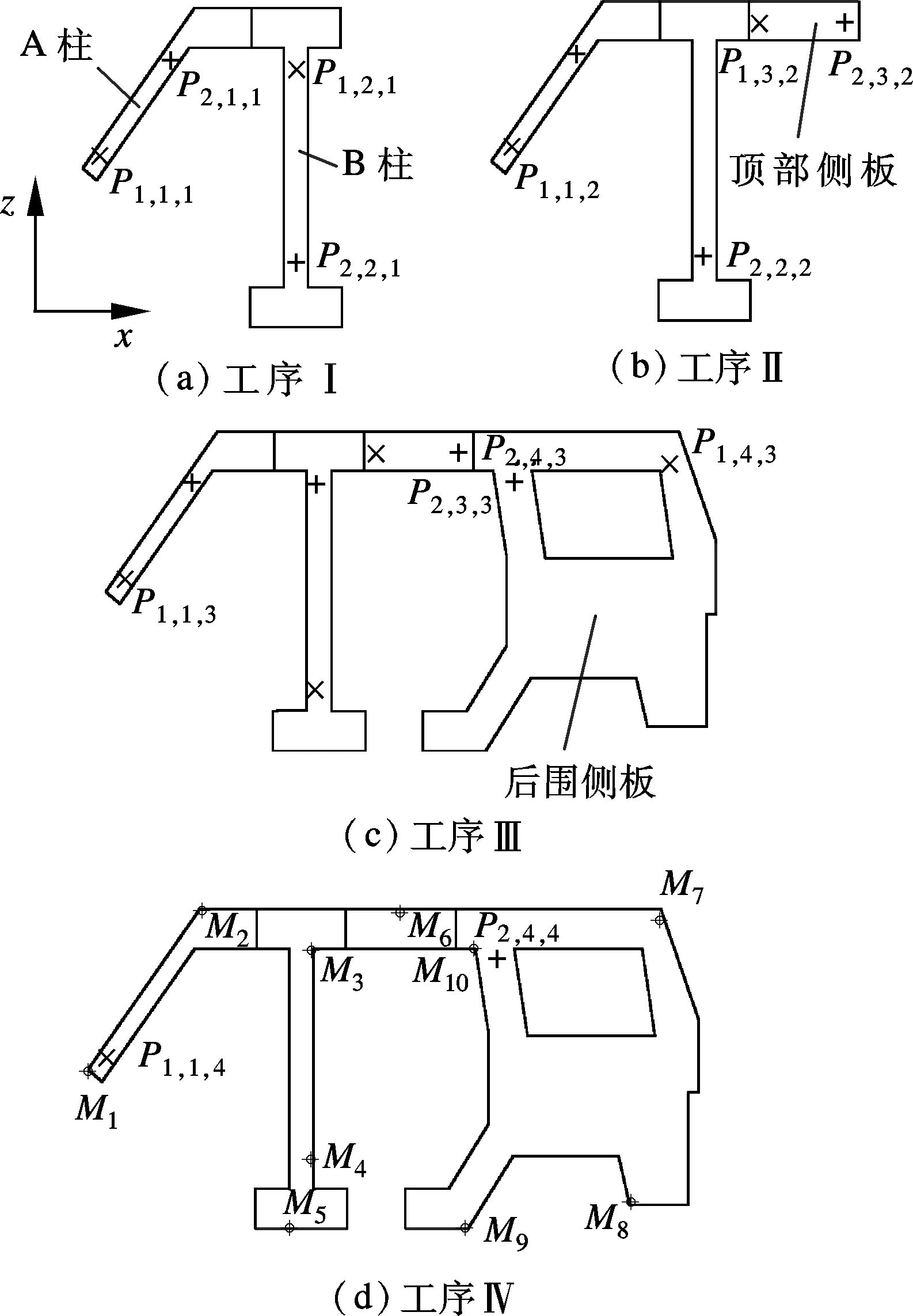
图1 某车辆侧板四工序装配过程

上述4道工序均使用了一面两销定位,若用定位销(P1,i,k,P2,i,k)(i代表零件,k代表工序)表示不同工序上使用的夹具,上述装配过程可表示为

[(P1,1,1,P2,1,1),(P1,2,1,P2,2,1)]Ⅰ→
[(P1,1,2,P2,2,2),(P1,3,2,P2,3,2)]Ⅱ→
[(P1,1,3,P2,3,3),(P1,4,3,P2,4,3)]Ⅲ→
[(P1,1,4,P2,4,4)]Ⅳ

式中,P1,i,k指定为圆柱销,限定2个自由度;P2,i,k为菱形销,限定1个自由度．上述装配过程均使用了A柱上的P1,1,k(1≤k≤4)作为共用定位销,因此,本文定义该类夹具系统为共用定位销的夹具系统．由于该夹具系统使用原有零部件上的销孔,避免了在装配体上重新开定位销孔,简化了工艺,所以应用广泛．而如何设计此类夹具系统的最佳布局则是个高维非线性问题,Kim等[8]所提出的传统准则需进行高维矩阵计算,运算成本巨大,本文提出一种面向此类系统布局设计的新设计准则,为此需首先建立数学模型．

2 改进的状态空间方程

共用定位销的多工序装配过程可用Jin等[7]提出的线性状态空间模型描述:

xk=Ak-1xk-1+Bkuk+wk

(1)

yk=Ckxk+vk

(2)

式中,Ak,Bk,Ck为与工序k特性相关的常数矩阵;xk-1和xk为对应工序的偏差向量;yk为观测向量;uk为偏差源;wk和vk为均值是零的系统噪声．式(1)为尺寸偏差传递方程,式(2)为观测方程．

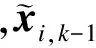
图2 工序k上零件i的偏差组成

图2中的过程可用公式表达为

Δxi,k=xi,k-xi,k-1=dr,i,k+df,i,k

(3)

式中,Δxi,k为零件i在工序k上增加的尺寸偏差量．如果记零件i进入装配线的初始工序为ki,那么,从零件i进入装配开始至工序k,其上所增加的偏差之和可表示为

xi,k=xi,0+Δxi,ki+Δxi,ki+1+…+Δxi,k

(4)

将式(3)代入式(4),可得

xi,k=xi,0+dr,i,ki+df,i,ki+dr,i,ki+1+

df,i,ki+1+…+dr,i,k+df,i,k

(5)

式中,xi,0为零件i进入装配前的原始尺寸偏差,不失一般性,记xi,0=0．式(5)可简化为

(6)

测量方程为

yi,k=Ci,kxi,k+vk

(7)

式(6)、(7)即为改进后的状态空间方程通式,对比式(1)、(2),其区别在于给出了单一零件偏差状态的构成及计算方法．由于装配体是由若干零件装配而成,若能计算出装配体上某一零件的偏差状态,则可由动力学分析得到装配体上所有零件和KPC的偏差状态．一般地,常用六维向量xi,k={δxi,k，δyi,k，δzi,k，δαi,k，δβi,k，δφi,k}T表示工序k上零件i的实际位置与理想位置的偏差．其中,δxi,k,δyi,k和δzi,k为零件i沿x,y,z坐标轴的移动偏差量;δαi,k,δβi,k和δφi,k为旋转角位移偏差量．若建立模型(1),随着工序增多,装配的零件也愈多．设需要装配的零件总数为n,则在最终工序N上得到的xN的维数为6n,即使考虑平面装配问题,xN的维数也有3n．以图1的一面两销为例,x4为12维．而建立模型(6)只需考虑单一零件的尺寸偏差传递和累积,其维数始终保持不变,这为后续问题的分析降低了难度．本文将运用式(6)、(7),对共用定位销的多工序装配过程进行分析,推导出新的夹具布局设计准则．

3 夹具布局优化新准则

3.1 引理[7]

本文关注的是多工序夹具系统布局中的平面优化设计问题,即一面两销中定位销的布局,故零件i的偏差状态可用3维向量表示,xi,k={δxi,k，δzi,k，δβi,k}T．根据文献[7],若零件为刚体,则有如下3个引理．

引理1当一个刚体零件与其理想位置有平移和旋转时,如果旋转角度δβ很小,那么在该零件上任取的2点的偏差{δxa,δza}T和{δxb,δzb}T有下列关系成立:

(8)

式中,偏差系数矩阵

(9)

其中，(xa,za),(xb,zb)为两点的理想坐标．

引理2零件偏差状态df,i,k与其上夹具定位销的随机偏差存在近似线性关系,假设定位销随机偏差与定位销之距相比很小,则有

(10)

式中,偏差系数矩阵

(11)

其中，Li,k为P1,i,k和P2,i,k两点间的欧几里得距离．

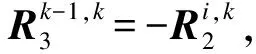
引理1表明了零件上任意2点间的尺寸偏差关系;引理2和引理3表明由夹具定位销随机误差造成的尺寸偏差df,i,k和重新定位带来的尺寸偏差dr,i,k均与定位销的随机误差存在近似线性关系．上述引理不仅在单一零件上适用,在装配体上也同样适用．

3.2 夹具布局优化新准则

对于共用定位销的多工序装配夹具布局,共用的定位销所在零件的偏差状态十分重要．若共用定位销点的零件尺寸偏差状态已知,则由引理1,其上所有KPC的偏差状态和与之刚性联接的装配体上的所有KPC的偏差状态均可知．

现假设共用的定位销在工序1的零件1上,为P1,1,1,工序N为测量工序,其上所有KPC的最终偏差状态由引理1和式(6)、(7)可得

x1,N=df,1,1+dr,1,2+df,1,2+…+dr,1,N+wN

(12)

(13)

式中,Kij为零件i上的第j个尺寸特征．再由引理1,与零件1刚性连接的任意零件的偏差状态和其上KPC的偏差状态可表示为

(14)

(15)

图3 零件i上的尺寸特征Kij

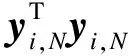
(16)

式(16)的证明如下:由引理2知

同理可得

(17)

对于x1,N,有

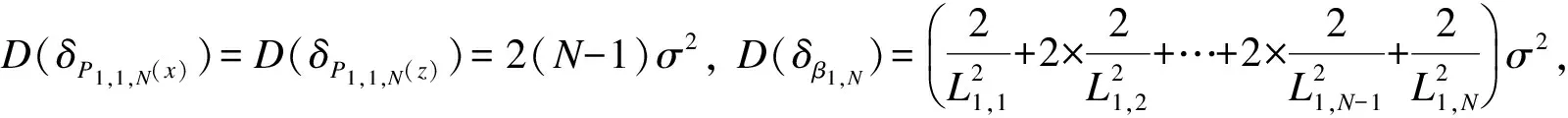
则

(18)

式(17)加式(18),得式(16),证毕．

由式(16)可知,tr(var(yi,N))是yi,N所有项方差的和,故可用其表示Kij的偏差水平．一般地,对于单一KPC,可取下式作为确定夹具布局的设计准则:

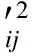
(19)

设装配过程有n个装配零件,每个零件上有ni个KPC,若使装配完成后装配体上所有KPC的偏差之和最小,也就是使下式取得最小值:

(20)

式(20)即为多工序夹具布局的设计准则．由于式(19)中(4N-2)σ2是个固定值,故被略去．Γ表示的是装配体上所有KPC对不同夹具布局的敏感程度．与Kim等[8]所提出的传统设计准则Smax需进行高维矩阵运算相比,Γ仅需进行平面定位点间的欧式距离计算,其计算效率必然得到提升．下面通过实例来验证将Γ用于夹具布局设计准则的有效性和计算效率．

4 实例验证与比较

以图1为算例,取定位销直径为10mm,采用交换算法[12]在Matlab7.0 中进行验证．电脑主频1.66GHz,双核处理器IntelT5500．分别采用Γ和Smax作为夹具布局设计准则,采用交换算法计算最优解,将所得最优解分别转化成Smax和Γ的当量值．所得结果如表1所示．

表1 Γ和Smax的比较 %

表1表明,采用Γ作为夹具布局设计准则能够得到与采用Smax作为夹具布局设计准则相近的结果,但计算所花费的时间却节约了14%．这说明,所提出的新准则能够保证解的有效性,同时计算效率更高．图4为采用Γ作为设计准则得到的夹具最优布局.

图4 Γ作为设计准则用交换算法得到的夹具布局

5 结语

在将夹具定位销的随机偏差作为影响装配体KPC的主要误差源时,使用传统多工序设计准则对夹具布局进行设计,需要计算复杂的高维矩阵,影响了计算效率．本文则通过建立单个零件偏差传递和累积的多工序状态空间模型,推导出了一种新的适用于共用定位销夹具方案的夹具布局设计准则．相较传统设计准则,该准则仅需计算定位销点的平面欧式距离．实例证明,使用该准则进行夹具布局设计不仅有效,而且能够节约计算成本,计算效率更高．

)

[1]Asada H,By A.Kinematic analysis of workpart fixturing for flexible assembly with automatically reconfigurable fixtures [J].IEEETransactionsonRobotandAutomation,1985,1(2): 86-93.

[2]Carlson J S.Quadratic sensitivity analysis of fixtures and locating schemes for rigid parts [J].JournalofManufacturingScienceandEngineering,2001,123(3): 462-472.

[3]Zhang X P,Yang W Y,Li M.An uncertainty approach for fixture layout optimization using Monte Carlo method [C]//ProceedingsoftheThirdInternationalConferenceonIntelligentRoboticsandApplications.Shanghai,China,2010: 10-21.

[4]Liu Z H,Wang M Y,Wang K D,et al.Multi-objective optimization design of a fixture layout considering locator displacement and force-deformation [J].InternationalJournalofAdvancedManufacturingTechnology,2012.doi:10.1007/s00170-012-4564-7.

[5]Selvakumar S,Arulshri K,Padmanaban K,et al.Design and optimization of machining fixture layout using ANN and DOE [J].InternationalJournalofAdvancedManufacturingTechnology,2012.doi:10.1007/s00170-012-4281-2.

[6]Dou J P,Wang X S,Wang L.Machining fixture layout optimisation under dynamic conditions based on evolutionary techniques [J].InternationalJournalofProductionResearch,2012,15(50): 4294-4315.

[7]Jin J H,Shi J J.State space modeling of sheet metal assembly for dimensional control [J].JournalofManufacturingScienceandEngineering,1999,121(4): 756-762.

[8]Kim P,Ding Y.Optimal design of fixture layout in multistation assembly process [J].IEEETransactionsonAutomationScienceandEngineering,2004,1(2): 133-145.

[9]Kim P,Ding Y.Optimal engineering design guided by data-mining methods [J].Technometrics,2005,47(3): 336-348.

[10]Tian Z Q,Lai X M,Lin Z Q.Robust fixture layout design for multi-station sheet metal assembly processes using a genetic algorithm [J].InternationalJournalofProductionResearch,2009,47(21): 6159-6176.

[11]Izquierdo L E,Hu S J,Du H,et al.Robust fixture layout design for a product family assembled in a multistage reconfigurable line [J].JournalofManufacturingScienceandEngineering,2009,131(4): 81-89.

[12]Cook R D,Nachtsheim C J.A comparison for constructing exact D-optimal designs [J].Technometrics,1980,22(3): 315-324.