无锡地铁盾构始发风险分析

刘 浔,范云中,丰土根,陆 跃

(1.河海大学岩土力学与堤坝工程教育部重点实验室,江苏南京210098;2.河海大学岩土工程科学研究所,江苏 南京 210098;3.镇江市农业委员会,江苏 镇江 212009;4.南京城建隧桥经营管理有限责任公司,江苏南京210017)

近年来,随着不断增长的交通需求,国内外各大城市纷纷投入巨资建造轨道交通,与此同时,一些新的施工工艺和技术也不断涌现出来。与传统的隧道施工方法不同,盾构法是一种集机械、土木、信息于一体的综合性的地下工程施工方法,具有快速、优质、安全、经济、对地层的适应性强、对环境影响小和劳动强度低等优点。从我国综合国力、环境保护、长远利益等方面考虑,新建地铁隧道中将有很大一部分采用盾构法施工。

经过几十年的工程实践和技术研究,我国在盾构施工方面解决了很多疑难问题,积累了丰富的实践经验。但是盾构始发的施工技术仍然是困扰隧道施工的难题,盾构始发是盾构施工中风险最大的环节,最容易发生工程事故。根据统计,在已运用盾构法建设的隧道工程中,70%以上的事故发生在盾构始发过程[1]。

前人的研究[2-6]表明,风险管理在隧道工程的应用研究在西方许多国家己经相当普遍,并己经成为隧道工程中必须实施的一项重要内容。但是现阶段研究的成果主要集中在定性分析方面,真正定量化的研究成果很少,定量的研究往往只是局限于可靠度的计算。本文根据无锡地铁1号线的工程地质与水文地质、周围环境条件、围护结构形式、使用的盾构机型等,对无锡地铁盾构始发风险进行系统的分析。

1 非线性模糊综合评判方法

1.1 风险等级的划分

为了有效把握工程的风险事故,指导风险决策的开展,需对不同的风险事故进行风险等级划分。一般来说,风险可表征为风险事故发生的概率和事故损失的乘积。包括风险发生概率等级标准(见下表1)和风险事故损失等级标准(见下表2),根据风险的基本定义,制定相应风险的等级标准和接受标准。

表1 风险发生概率等级标准

表2 风险事故损失等级标准

1.2 基于模糊综合评判法的风险评估简介

引进模糊数学理论[7-8],建立盾构始发施工风险分析模糊综合评判模型对应的计算模型,具体如式(1)。

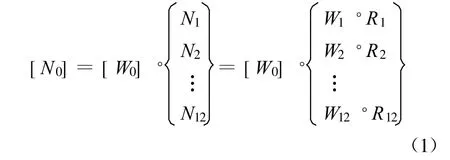
式中,[Ri]为12个二级影响因素[pi]分别对应的一级评价指标[pij]的隶属度向量所构成的一级评判矩阵。·为模糊算子。Wi为12个二级风险因素[pi]分别对应的一级风险指标[pij]由于其间的重要程度不同所构成的权向量,[Ni]为12个二级风险因素[pi]分别对应的一级风险因素评价指标[pij]的一级评价结果向量,即二级评判矩阵中的向量;[N0]为盾构始发端的二级(最终)评判结果向量,即盾构始发端风险分级的隶属度向量(五维向量)一般根据[N0]中的5个元素的大小及最大隶属度原则可确定盾构始发端风险等级。

由于分为五个等级来确定风险比较粗糙,因此,有必要通过定量化来确定更细的分级结果,所以采用百分制的方法,先确定各类等级所对应的评分值,然后由下述方法计算风险等级值,即:

式中:aj为各个等级的评分值,为了简化计算,取对应区间的中值计算;nj为一级或者二级评判结果向量[Ni]的第j个值;Qk为评判结果定量化处理值,其所在区间对应等级即为最终的风险等级。

2 无锡地铁盾构始发风险识别

结合无锡地铁1号线的地质条件、加固方式分析,对盾构始发风险因素进行合理分类,从而建立盾构始发端施工风险分析的模糊综合评判指标体系,其中盾构始发端包括盾构机吊装和拼装事故、拆除封门后出现涌土和流砂、洞口土体流失、盾构推进轴线偏离设计轴线、后盾系统出现失稳、盾构机无法正常推进甚至后退;盾构到达端包括盾构姿态突变、偏离目标井或对接错位、盾构基座变形、洞口失效漏水、盾构到达引起基坑塌方等12个二级指标和相应的39个一级指标。综合评判指标体系如表3所示。

3 无锡地铁一号线盾构始发风险评估

3.1 风险源权重的确定

通过模糊层次分析法对无锡地铁1号线始发各风险源权重进行计算。

要确定评判因素的权重,须考虑参数β的选择,因为权重wi是关于β的函数。而 β代表的是决策者的分辨能力。本文中,由于风险一级评价指标的相关联的指标个数不是太多(≤5),影响权重大小的参数β不必取很大的值,综合考虑取β=50,二级指标权重也取β=50。

通过1～9标度法[9]构造出判断矩阵,然后将判断矩阵转换为模糊标度下的比较矩阵,再计算出各指标权重结果如表4所示。

表3 综合评判指标体系

3.2 各指标突出影响程度的确定

一级评价指标的最终突出影响程度系数取值如表5所示。

3.3 风险源的风险评分值和隶属度的确定

结合无锡地铁一号线盾构始发端的具体情况确定一级评价指标的风险评分值Qi如表6所示。

表4 各指标权重结果

采用折线方法确定一级指标各评价指标的隶属度,公式如下:

将表6中一级评价指标的评分值代入式(3)～式(7)中,则可以确定各个风险指标对应各个风险等级的隶属度的值r′ij,具体的隶属度取值见表7。

3.4 一级评价指标的评定

为了使变换后的矩阵与原矩阵具有较好的一致性,本文将各个一级评价指标的隶属度值分别构成的原始模糊矩阵通过式 rij=10×r′ij转换,转换以后的矩阵即为可进行非线性运算的模糊评判矩阵[Ri](i=1,2,3,…,12),然后由确定的各个一级评价指标的权重[wi](i=1,2,3,…12)、最终的突出影响程度系数λji、非线性模糊评判矩阵[Ri](i=1,2,3,…,12)进行非线性运算,得到一级评判结果向量[Ni](i=1,2,3,…,12),其计算结果见表8。

表5 最终的各个评价指标的突出影响程度的取值

表6 无锡地铁一号线风险源的风险评分值

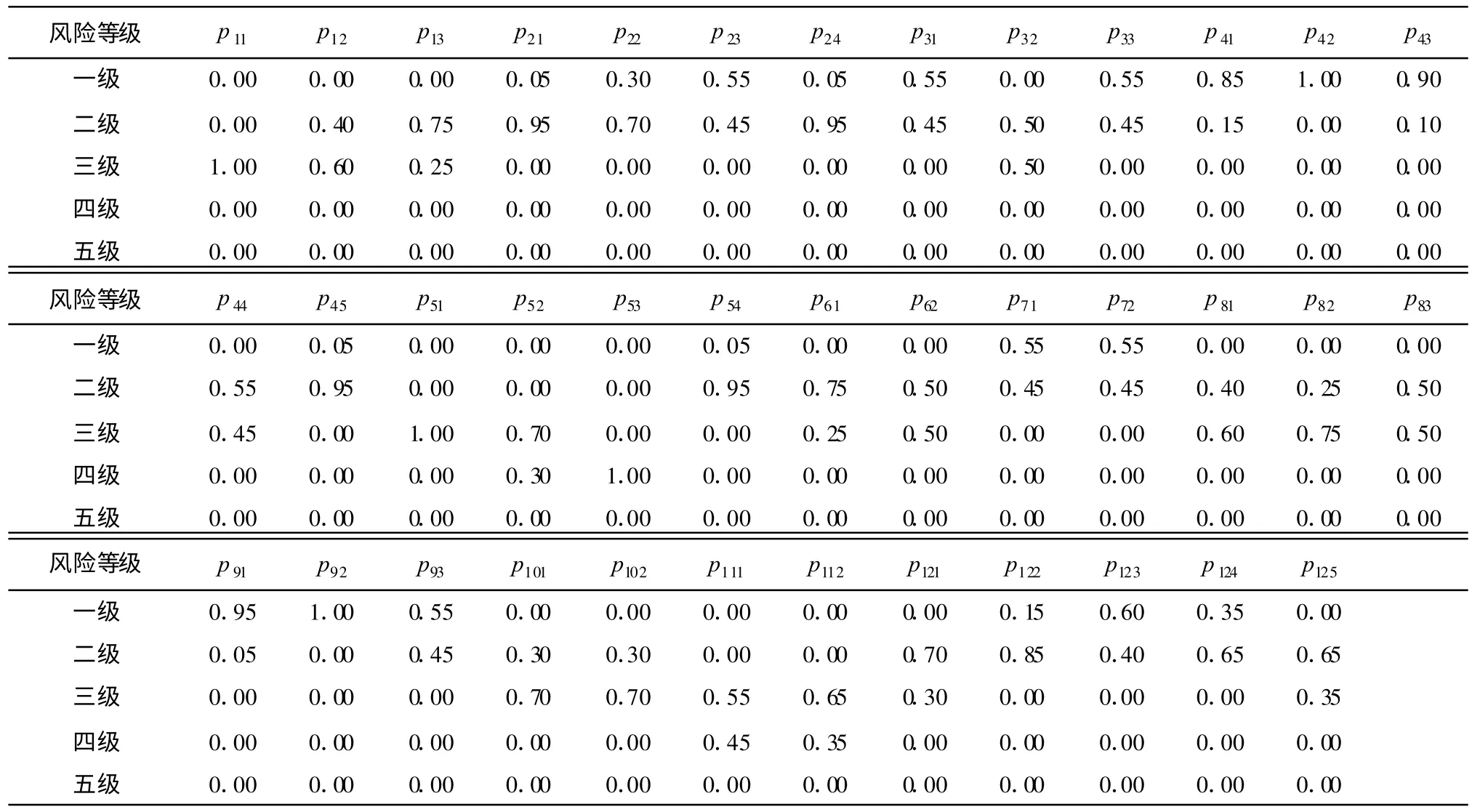
表7 无锡地铁一号线风险源的隶属度

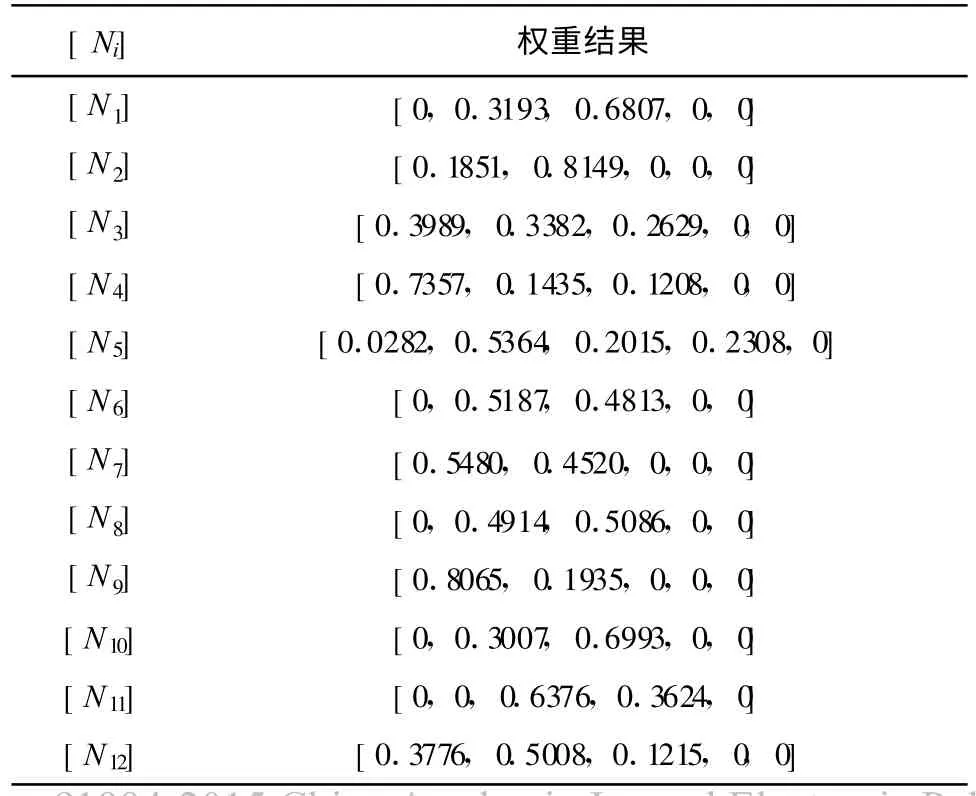
表8 [Ni]计算结果

3.5 二级评价指标的评定

在得到一级评价指标的评判结果向量[Ni](i=1,2,3,…,12)以后,根据式(2)计算二级评价指标的风险评分值,再根据式进行转换计算,得到二级指标的最终突出影响程度系数,见表9。

利用式(2)对最终的二级模糊综合评判结果向量[N0]进行定量化计算,得到风险评分值 p0和分别为124.68和127.55。

表9 二级指标的最终突出影响程度系数

由此可知,无锡地铁一号线的盾构始发端的风险等级为二级110≤Q≤130,由于其接近于中值120,所以属于二级中等;无锡地铁一号线的盾构到达端总的风险等级为二级110≤Q≤130,由于其接近于上限130,属于二级偏一级。

为了证明上述方法的合理性,本文采用线性的方法(模糊层次分析法确定权重)来进行风险评估,评判结果向量为:

风险评分值为p0和p′0分别为124.98和127.87。

通过线性风险评价,无锡地铁1号线盾构始发端的风险等级属于二级110≤Q≤130,所以属于二级中等,到达端总的风险等级为二级110≤Q ≤130,属于二级偏一级。

4 结 论

本文针对盾构始发端施工中质量与安全影响因素的特点,进行风险分析,选取主要的风险影响因素,考虑其间的层次性和模糊性,建立了盾构始发端施工风险分析的模糊综合评判模型,全面、合理地反映了各种因素对盾构始发端施工风险的影响。可以得到的结论如下:

(1)采用模糊数学理论,在研究风险评判等级、影响因素以及评价指标的隶属度和权向量确定方法等的基础上,建立盾构始发端施工风险分析的模糊综合评判方法,可以使盾构始发端施工风险分析方法更趋合理性与可操作性。

(2)采用模糊层次分析法来计算权重,并引进模糊矩阵合成算子进行计算,突出评判过程中不利因素对盾构始发端施工质量与安全风险评估结果的突出影响,可以使得评判结果更具有合理性。

(3)通过建立非线性模糊综合评判法对无锡地铁1号线盾构始发进行风险评价,再通过线性模糊综合评判法进行比较与验证,结果是一致的,而在无锡地铁1号线盾构始发的实际施工过程中没有出现较大的事故,也间接证明了本文方法的合理性。

[1]周文波.盾构进出洞施工风险分析及防治[C]//地下工程建设与环境和谐发展——第四届中国国际隧道工程研讨会文集.上海:同济大学出版社,2009:156-165.

[2]Sturk R,Olsson L,Johanssen J.Risk and decision analysis for large underground projects,as applied to the stockholm ring road tunneling[J].Tunneling and Underground Space Technology,1996,11(2):157-164.

[3]Kampmann J,Summers J W,Eskesen S D.Risk assessment helps select the contractor for the copenhagen metro system[C]//World Uunnel Congress 98 Tunnels and Metropolises,1998,(1):123-128.

[4]Reilly J J.Management process for complex underground and tunneling projects[J].Tunneling ＆ Underground Space Technology,2000,3(2):31-44.

[5]Mitchell B.Use of the most likely failure point method for risk estimation and risk uncertainty analysis[J].Journal of Hazardous Materials,2002,91(1-3):1-24.

[6]Woude S V,Jonker J H.Risk management for the betuweroute shield driven tunnels[C]//Claiming the Underground Space.2003:1043-1049.

[7]李洪兴,汪 群,段钦治.工程模糊数学方法及应用[M].天津:天津科学技术出版社,1993:104-132.

[8]宋晓秋.模糊数学原理与方法[M].北京:中国矿业大学出版社,1999:201-204.

[9]曹文贵,张永杰.岩体质量分类区间非线性模糊评判方法[J].岩石力学与工程学报,2007,33(31):620-625.