三维随机渗流场下英德北堤防护工程渗透破坏风险分析

刘 军,王 媛

(1.河海大学岩土力学与堤坝工程教育部重点实验室,江苏南京210098;2.河海大学岩土工程科学研究所,江苏南京210098)

1 工程概况

英德市地处广东省中北部,北江自北向南贯穿其全境。城区原有堤防大多为早期群众运动所建,工程质量差,防洪标准低(堤顶约32.0 m～33.0 m),而且,英德城区地势较低洼,高程多在25 m～33 m之间。因此,洪涝灾害十分严重,几乎是年年有小灾,三年一大灾,甚至一年数灾。为减少洪水灾害,英德市规划对原有防洪堤进行重修加固。其中,在城区西岸北堤防护工程重修堤防 4段,总长13 233.739 m,包括江湾、矮山坪、白沙、岭背塘等堤段。根据勘探资料表明,白沙段存在破坏的风险最大。因此,本文针对白沙段进行分析。

白沙防洪堤段长5 114.692 m,现状堤段内侧为河流一级阶地。在接近河堤内侧,中下游有较多鱼塘分布,该类鱼塘为早期建河堤取土而形成。河堤外侧,上游以一级阶地为主,下游主要为河漫滩,河漫滩宽度最大大于100 m。根据勘察资料可知,该段堤基主要为双层结构,上部为细粒的壤土,下部为粗粒的砂层,下伏基岩为石灰岩。新建堤防洪标准为2级,堤身结构为均质土堤,沿旧防洪堤内侧布置,局部位置修顺,且在靠近临水面一侧修建了防渗墙。防洪堤迎水坡坡度采用1∶2.5并设置混凝土护坡,背水坡坡度采用1∶2,堤顶宽度统一为8 m,堤顶路面高程36.725 m。考虑施工时运输的需要,沿堤脚布置一条10 m宽的施工道路,并将堤内侧局部低洼鱼塘填平。对于加高的堤身填土采用附近料场土料。

大量的历史资料表明,渗透破坏问题造成的危害大、范围广,且易造成堤防失事灾害。而且堤防工程中存在着许多不确定性因素,如土体的物理参数、各地层的渗透系数、水位变化等,因此基于可靠度理论对堤防工程进行渗透风险分析[1]就显得非常客观和必要了。

2 计算原理模型及参数

2.1 计算原理

基于一阶Taylor随机有限元法[2],本文对三维稳定渗流场进行了随机有限元分析。在进行随机有限元分析中,将渗透系数处理为各向异性平稳随机场,利用三维可分向量的局部平均法进行离散;然后基于一阶摄动法随机变分原理,推导出了三维非稳定渗流场的随机有限元列式,并结合一阶Taylor展开随机有限元法得到稳定渗流场响应量(水头和水力梯度)的随机统计量公式。

在对堤防进行可靠度风险分析时,功能函数取为整个渗透破坏危险区域的单位体积土体的抗力与破坏力之差,在计算中将Jx,Jz,φ,C等视为随机性量,再利用几何法[3]求解可靠度指标。具体分析中将考虑堤身临水坡和背水坡渗透破坏两种模式,并且每种形式又分为沿坡面向下滑坡和垂直坡面顶冲破坏两种[4]。

(1)背水坡面土体在渗透力作用下沿坡面向下滑动破坏如图1(a),相应的功能函数为

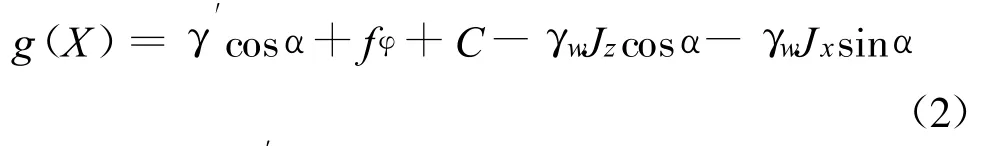
g(X)= γwJzsinα+fφ+C-γwJ xcosα-γ′sin α(1)其中,fφ=(γ′cosα-γwJzcosα-γwJxsinα)tan φ;α为坡面与水平方向夹角;Jx为水平方向x向的水力梯度;φ为土体的内摩擦角,tan φ为相应的内摩擦系数。(2)背水坡面土体在渗透力作用下垂直坡面顶冲破坏如图1(b),相应的功能函数为

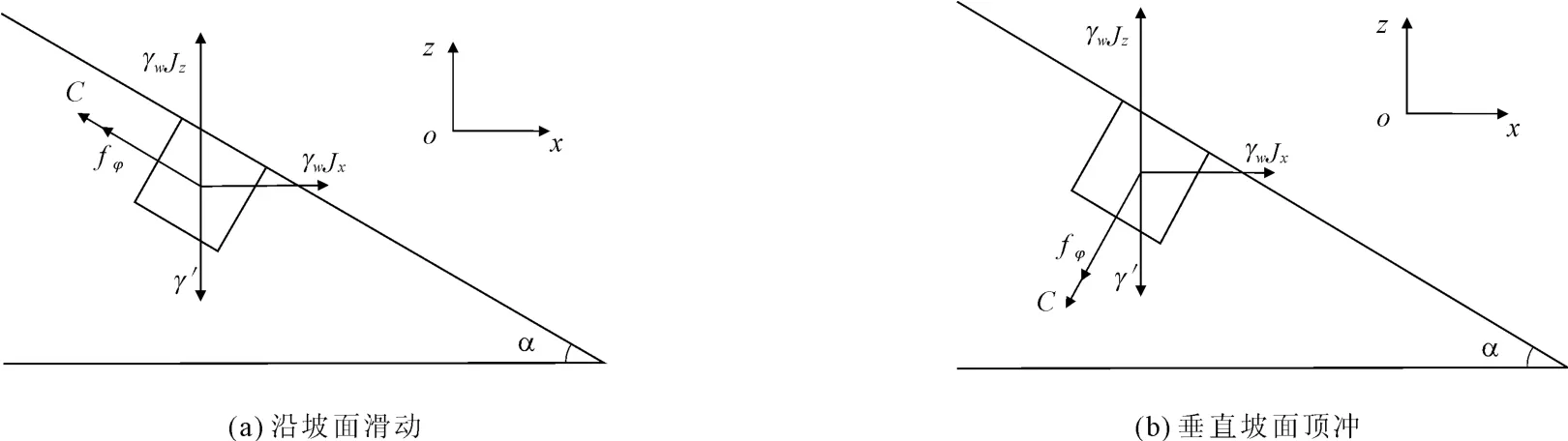
图1 背水坡面单位土体受力图

其中 fφ=(γ′sinα+γwJxcos α- γwJzsinα)tan φ(3)临水面土体在渗透力作用下沿着坡面向下滑动破坏如图2(a)所示,相应的功能函数为

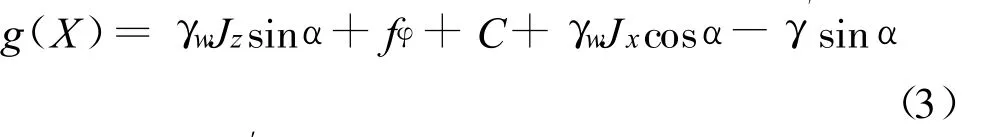
其中 fφ=(γ′cosα-γwJzcosα+γwJxsin α)tan φ

图2 临水坡面单位土体受力图

(4)临水面土体在渗透力作用下垂直坡面顶冲破坏如图2(b)所示,相应的功能函数为

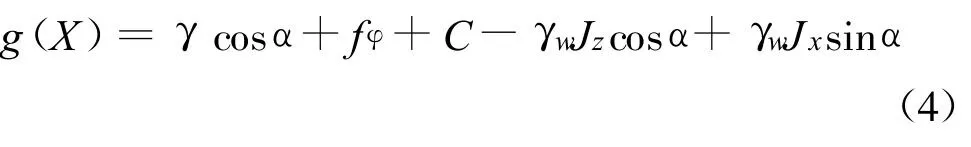
其中 fφ=(γ′sinα-γwJxcos α- γwJzsinα)tan φ

另外,在进行上述求解时渗流场中水力梯度统计量值可由之前提出的渗流随机有限元法获得。

2.2 计算模型

根据以上资料,在建模时可以将旧堤及新建堤防典型堤段截面简化为图3,并沿堤轴线长度方向取长度为290 m,填平前下游鱼塘的尺寸取为30 m×50 m×2 m。旧堤的堤身土采用和堤基表层土相同类型,新堤的堤身加高填土选用附近料场土料。可以看到,旧堤原堤顶高程为32.725 m,新堤的堤顶高程为36.725 m,在计算时取堤内侧水位为地面高程27.725 m。在随机场离散过程中,对不同土层分区域考虑并视为相互独立,而同一土层在不同主向上分别视为独立平稳随机场,相关函数[5]选取高斯相关函数 ρω=exp[(-πΔx2-πΔy2)/2500]·exp(-πΔz2/9),由此,旧堤和新建堤离散出的随机变量数目分别为111个和153个。

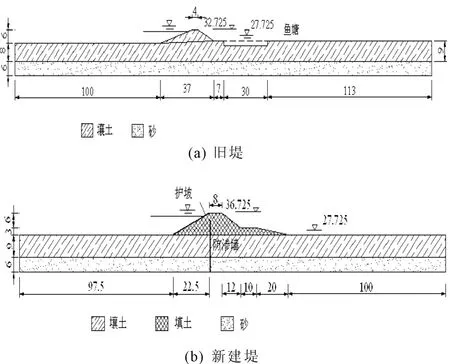
图3 旧堤及新建堤断面图(单位:m)

2.3 计算参数

表1给出了英德水文站年最高水位频率统计结果。对于土体材料参数,此处将渗透系数、抗剪强度参数等视为随机量。其中渗透系数服从对数正态分布[6],粘聚力及摩擦角均服从正态分布,得到的参数统计如表2～表4。表中试验值为白沙段试样的试验结果,而将相邻堤段的相同类型土的试验结果作为先验值,可以通过Bayes法得到参数的后验估计值[7]。对于土体的重度我们视为确定性量,对于壤土取为19.4 kN/m3,对于料场土取为19.0 kN/m3。

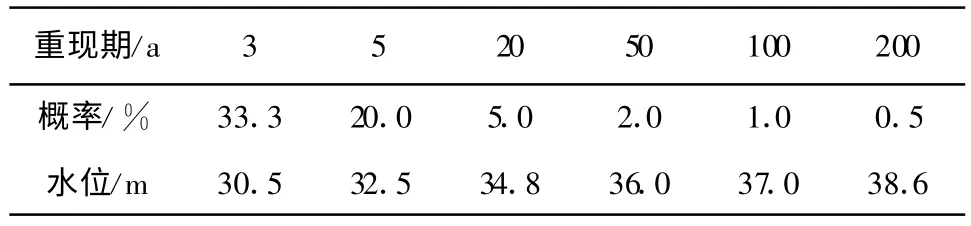
表1 年最高水位频率统计

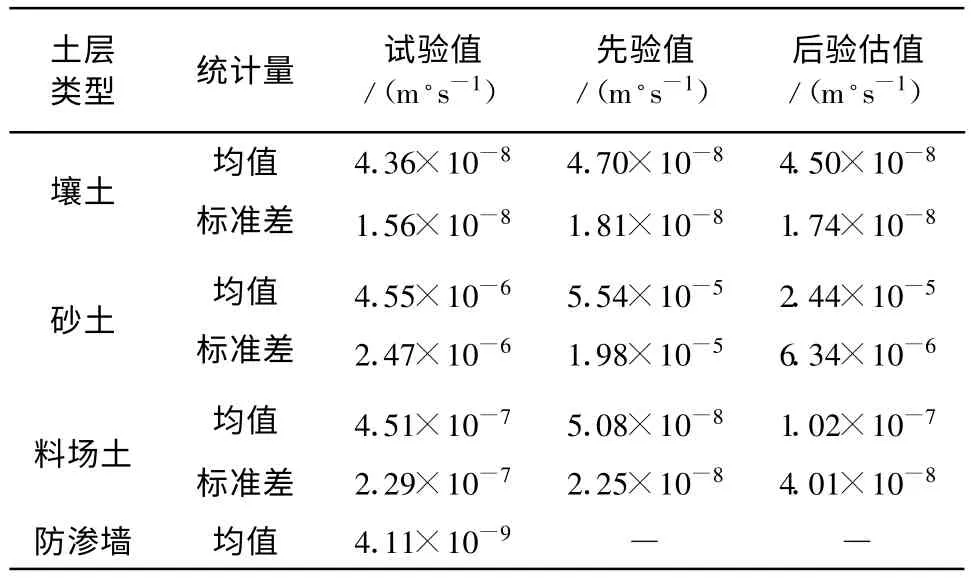
表2 渗透系数统计量

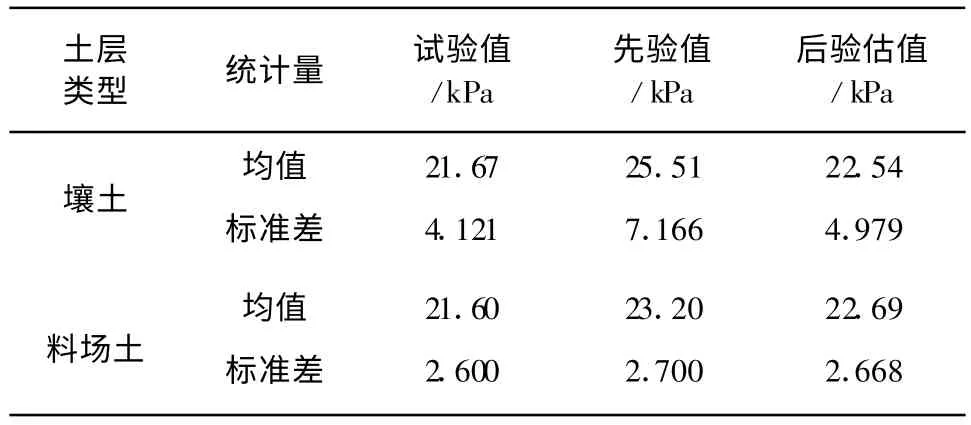
表3 粘聚力统计量

表4 内摩擦角统计量

3 计算分析

3.1 渗流场计算

在进行计算时,假设水位频率曲线服从正态分布,则根据表1得到的统计结果可以拟合出水位频率曲线函数为N(29.092,3.529)。在进行渗流场计算时将对不同水位下进行不同工况的求解。对于旧堤,取五种工况,迎水面水位分别为28.5 m,29.5 m,30.5 m,31.5 m,32.5 m。对于新堤,也取五种工况,迎水面水位分别为30.5 m,32.5 m,34.8 m,36.0 m,36.7 m。各工况下的水力梯度统计量最大值如表5～表6。

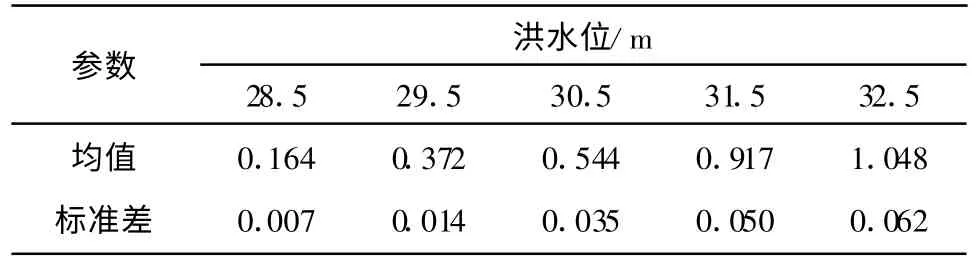
表5 旧堤在不同洪水位下稳定渗流水力梯度统计量最大值

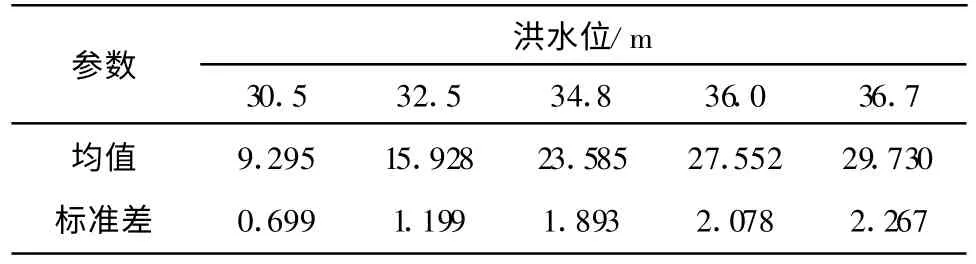
表6 新建堤在不同洪水位下稳定渗流水力梯度统计量最大值

3.2 堤防渗透破坏风险分析

(1)旧堤渗透破坏风险概率

表7给出了研究工况下发生渗透破坏的概率及相应安全系数的计算结果。由表7中数据可以看到,在稳定渗流情况下,背水坡面在洪水位较高时发生渗透破坏的概率虽然并不大,但是其较低洪水位时发生破坏的概率增大很多;对于临水坡面其发生土体渗透破坏的概率则相对比较大,特别是在高水位时。

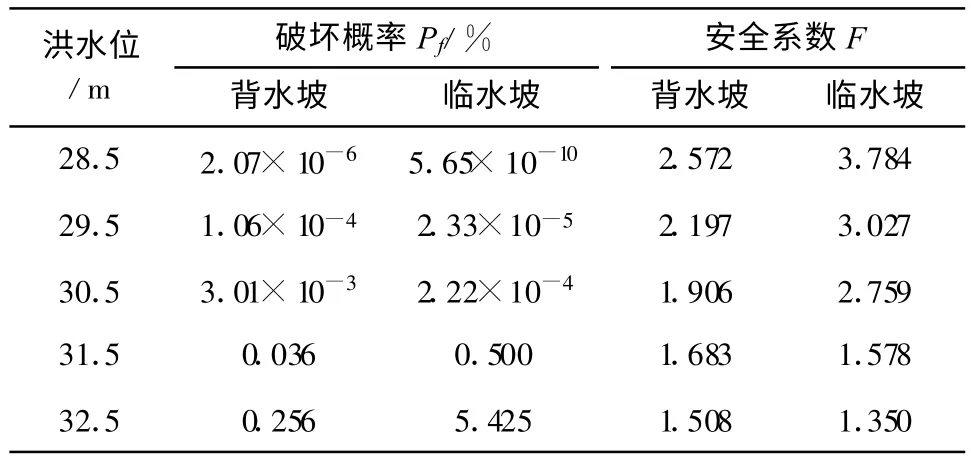
表7 旧堤在不同洪水位下渗透破坏风险概率

对表7中数据进行洪水位和风险概率之间的关系曲线拟合,可以得到曲线如图4。由图4可以看到,对于背水坡渗透破坏,在洪水位不太高时,破坏概率始终保持在一个很小值,当洪水位增高到一定值时,其值会有一个较大地增长,然后随着水位的增高,这种增长趋势变缓。对于临水坡渗透破坏,破坏概率变化规律和背水坡相似。

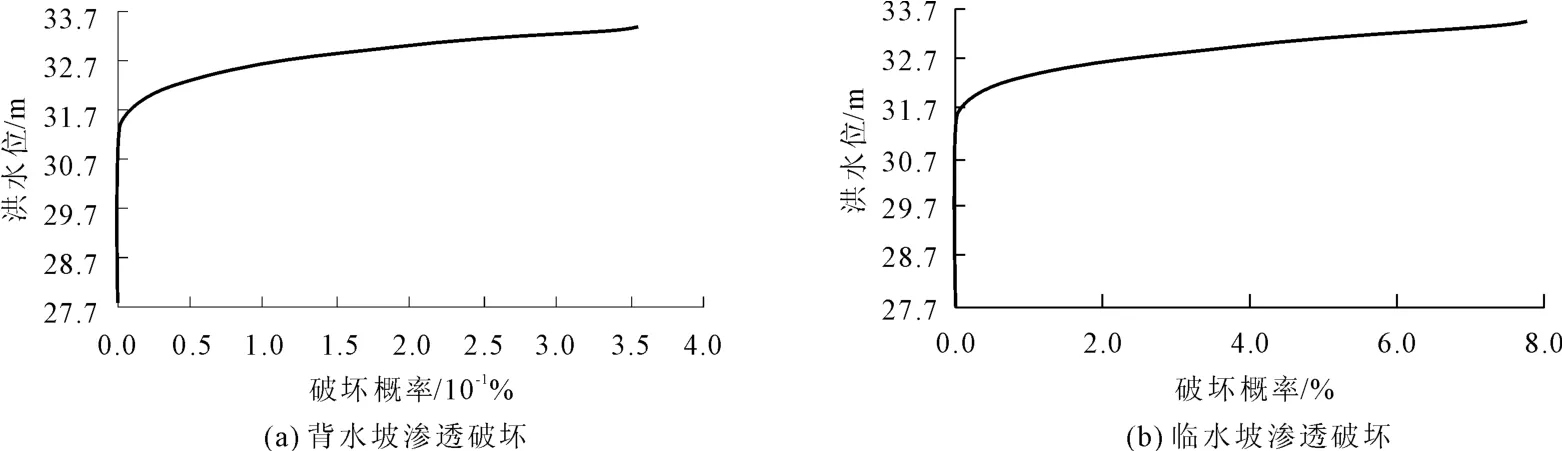
图4 旧堤各破坏模式风险概率与洪水位关系曲线

(2)新建堤渗透破坏风险概率

表8给出了新建堤在研究工况下发生渗透破坏概率及相应的安全系数计算结果。由表8中数据可以看到,和旧堤相比,在同一洪水位下背水坡发生渗透破坏的概率大大地降低了,即使在很高水位时也保持在一极小值,可以认为此时其破坏概率约等于0。

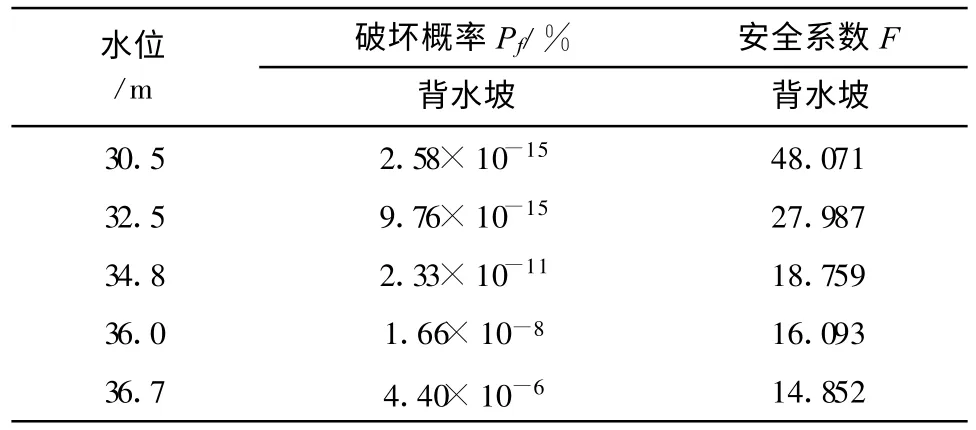
表8 新建堤在不同洪水位下渗透破坏风险概率

图5给出了新建背水坡渗透破坏概率与洪水位关系曲线。由图5可以看到,其风险概率值非常小,且随着洪水位的升高风险概率值增长较平缓,这体现了防渗墙设置的效果。

图5 新建堤背水坡渗透破坏风险概率与洪水位关系曲线

(3)风险分析结果

根据上面拟合得到的各破坏模式风险概率与洪水位关系曲线,并结合洪水频率函数,可以分别得到旧堤以及新建堤在所有可能洪水位下的各种破坏模式的总风险概率,如表9。

这里,我们将对旧堤及新建堤采用确定性分析法进行安全性评价。对于旧堤,其防洪标准为3 a～5 a一遇,对于新建堤,其防洪标准为50 a一遇。根据洪水位频率曲线,可得50 a一遇洪水相应的设计洪水位为36.34 m。对于旧堤,该设计水位远远大于堤顶高程,因此我们在对其进行结构安全性评价时不取设计洪水位作为评价标准,而是取洪水位等于堤顶高程时的安全评价结果。同样,我们可以确定该堤防发生渗透破坏的允许安全系数为1.5[8]。于是结合表7～表8中所得安全系数计算结果,可以得出旧堤及新建堤的确定性分析法的安全评价结果见表10。

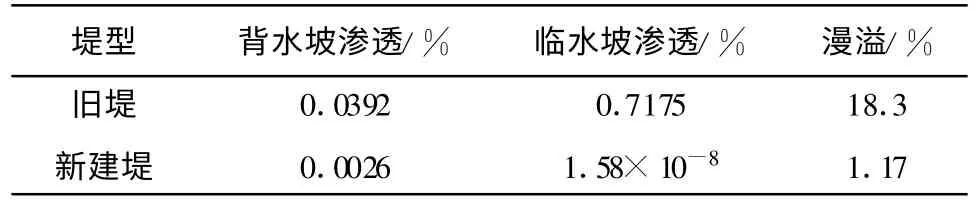
表9 总风险概率

表10 旧堤及新建堤确定性分析安全评价

结合表9、表 10可以看到,对于旧堤,首先,其发生漫溢破坏的概率达到18.4%,而确定性分析法得到的结果也表明其不满足安全要求,说明该堤极容易发生破坏;其次,即使洪水位较低不会发生漫溢破坏,也会发生临水坡的渗透破坏,并且可用相应的破坏概率值来描述;再次,对于其它破坏模式,确定性分析法得到的结果表明其是安全的,然而若同时考虑风险分析结果则可以看到,其仍具有一定的破坏概率值,并不足以忽略。而对于新堤,确定性分析法得到的结果表明各破坏模式均满足安全要求,这说明新建堤在安全性能上有了很大地提高,体现了修建新堤的意义。

4 结 语

本文通过对渗流场的随机分析得到水力梯度的统计量,并在此基础上利用概率理论对英德市北堤防护工程渗透破坏进行了风险分析。在分析中首先选取典型堤段,并对重修加固前的旧堤以及新建堤建立了计算模型,计算了不同水位下新堤与旧堤的水力梯度统计量,然后再利用可靠度分析求得各工况下旧堤及新建堤的渗透破坏概率,并分析了其渗透破坏的规律,对于旧堤,在洪水位不太高时,破坏概率较小且变化不大,当洪水位增高到一定值时,其值会有一个较大地增长,然后随着水位的增高,这种增长趋势变缓;对于新堤,其风险概率值非常小,且随着洪水位的升高风险概率值增长较平缓。最后,

对比了旧堤与新堤的综合风险概率,发现新建堤防后发生渗透破坏的风险概率明显降低,而且新堤各破坏模式均能满足安全要求,说明对旧堤改建是十分有意义和必要的。

[1]李青云,张建民.长江堤防工程风险分析和安全评价研究初论[J].中国软科学,2001,(11):112-115.

[2]王 飞,王 媛,倪小东.渗流场随机性的随机有限元分析[J].岩土力学,2009,(11):3539-3542.

[3]吕泰仁,吴世伟.用几何法求构件的可靠指标[J].河海大学学报,1998,16(5):86-93.

[4]王 飞.三维非稳定随机渗流场堤防失稳风险分析[D].南京:河海大学,2010.

[5]杨金忠,蔡树英,黄冠华,等.多孔介质中水分及溶质运移的随机理论[M].北京:科学出版社,2000.

[6]施小清,吴吉春,袁永生.渗透系数空间变异性研究[J].水科学进展,2005,16(2):210-215.

[7]WilsonH.Tang著.工程规划与设计中的概率概念[M].孙芳垂,陈星焘,胡世平,等译.北京:冶金工业出版社,1985.

[8]中华人民共和国建设部.GB 50286-98.堤防工程设计规范[S].北京:中国计划出版社,1998.