二阶电路零输入响应的GUI设计

冯巧红

滁州职业技术学院机电系，安徽滁州，239000

随着全球产业的信息化、自动化、智能化的发展，对电气类专业人才的需求日渐增长。电路理论是机械电子、通讯技术、信息工程以及自动化专业的一门重要的专业技术基础课，是电气类专业人才必备的理论基础。然而，由于电类课程中很多知识理论性较强，在学习过程中存在公式多,电路图、波形图和示意图多以及电路分析的方程和定理推理严谨等一系列问题，使得教师的教和学生的学成为教学中的共性问题。近几年，随着计算机技术的飞速发展，仿真技术在教学中的应用越来越受到广大师生的青睐，MATLAB GUI 设计工具因其可以设计出符合各种功能要求的人机交互界面以及快速产生各种图形对象的开发环境，尤其在分析计算电路动态响应、绘制响应波形方面，有着一般软件无法比拟的优势，因而倍受广大电气类师生们的青睐。笔者利用MATLAB GUI设计了二阶电路在零输入响应下存在的三种状态对应的波形图，为师生们直观而形象地学习这部分内容提供一个很好的参考平台。

1 二阶电路的数学描述

二阶电路如图1所示，设电路原来在稳态，在t=0时开关闭合，电路进入暂态。

根据KVL可得：uR+uL+uC=0

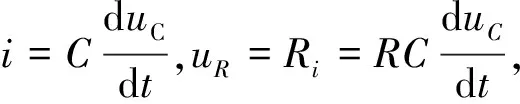
整理方程可得：

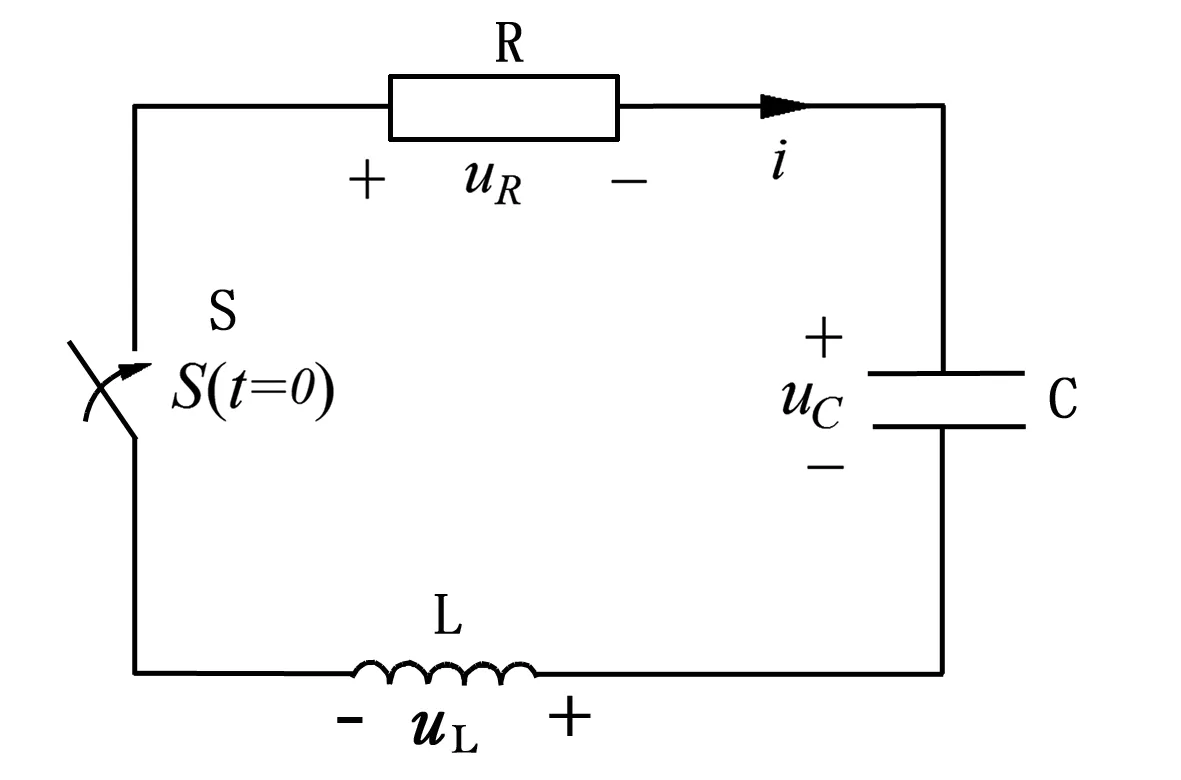
图1 二阶电路图

该电路的初始条件有uC(0)，iL(0)，此处令初始条件为uC(0)=U0、iL(0)=0，下文也都以此作为初始条件。上述微分方程的特征根方程为：

LCp2+RCp+1=0

可知方程的根为：

根据电阻R、L、C的取值情况，电路的工作状态可分三种情况来讨论。

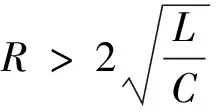
uC(t)=A1ep1t+A2ep2t

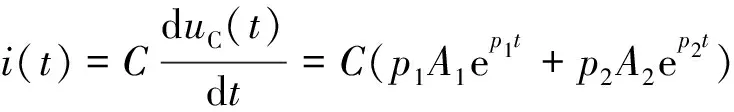
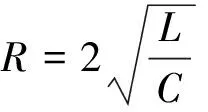
uC(t)=(A1+A2)e-δt

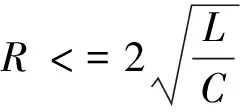
2 基于MATLAB的二阶电路零输入响应的GUI设计

为了便于分析，下面在MATLAB的GUI的环境中设计分析界面。首先在布局编辑器中选用合适的控件，形成框架：建立3个坐标轴对象，分别用来显示过阻尼响应、临界阻尼响应和欠阻尼响应；建立两个按钮，分别用来输入数据、计算并绘制响应曲线和结束程序；建立9个静态文本标签，其中3个用来显示输入的3组不同的R、L、C的值以产生过阻尼、临界和欠阻尼响应，其余6个文本标签用来标注相应控件的提示和显示输入的数据。具体界面设计如图2所示，保存为指定文件名。

设置第一个按钮的“String”为“分析”，作为数据输入、结果分析及绘制相应的响应曲线。编写代码实现该按钮执行指定的功能，也就是先依次弹出3个输入对话框以输入并获取R、L、C的数值，并且在相应的文本标签中显示出来，然后将所获数据转化为文本数据进行对应的结果分析和计算，同时在对应的3个坐标轴上绘制对应的响应曲线。具体实现代码如下：

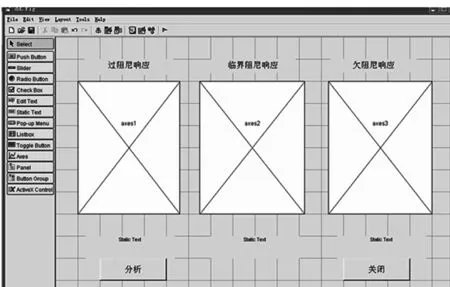
图2 GUI界面

function pushbutton1_Callback (hObject,event data,handles)

t=0:0.005:50;

str={'R','L','C','U'};

abcData=InputDlg(str,'输入R L C U2的值',1); %从输入对话框输入R L C U0的值

if ～isempty(abcData)

R=str2double(abcData(1));

L=str2double(abcData(2));

C=str2double(abcData(3));

U=str2double(abcData(4));%从输入对话框中获取R L C U0的数值

set(handles.text1,'String',strcat('R=',abc Data(1),',L=',abcData(2),',C=',abc Data(3),',U0=',abcData(4))); %将R L C U0的值显示在对话框中

x1=R/(2*L);x2=1/(L*C);P1=-x1+sqrt(x1^2-x2);P2=-x1-sqrt(x1^2-x2);

A1=P2*U/(P2-P1);A2=P1*U/(P1-P2);%计算相关参数

uc1=A1*exp(P1*t)+A2*exp(P2*t);

i1=C*P1*A1*exp(P1*t)+C*P2*A2 *exp(P2*t);

axes(handles.axes1);%选定第一个坐标轴绘制过阻尼响应曲线

set(handles.axes1,'XMinorTick','on');

plot(t,uc1,'k',t,i1,'r');%绘制过阻尼响应曲线

end

t=0:0.1:4;

abcData=InputDlg(str,'输入R L C U0的值',1);

if～isempty(abcData)

R=str2double(abcData(1));

L=str2double(abcData(2));

C=str2double(abcData(3));

U=str2double(abcData(4));

set(handles.text2,'String',strcat('R=',abcD ata(1),',L=',abc Data(2),',C=',abc Data(3),',U0=',abcData(4)));

x1=R/(2*L);

uc2=U*(1+x1*t).*exp(-x1*t);

i2=-U/L*t.*exp(-x1*t);

axes(handles.axes2);

plot(t,uc2,'K',t,i2,'r');

end

t=0:0.001:20;

abcData=InputDlg(str,'输入R L C U1的值',1);

if～isempty(abcData)

R=str2double(abcData(1));

L=str2double(abcData(2));

C=str2double(abcData(3));

U=str2double(abcData(4));

set(handles.text3,'String',strcat('R=',abcD ata(1),',L=',abc Data(2),',C=',abc Data(3),',U0=',abcData(4)));

x=R/(2*L);w0=1/sqrt(L*C);w=sqrt (w0^2-x^2);

uc3=w0/w*U*exp(-x*t).*sin(w*t+atan(w/x));

i3=C*w0/w*U*exp(-x*t).*(w* cos(w*t+atan(w/x))-x*sin(w*t+atan (w/x)));

axes(handles.axes3);

plot(t,uc3,'k',t,i3,'r');

end

设置第二个按钮的“String”为“结束”，用来结束程序。调用其Callback函数执行关闭图形，代码如下：

function pushbutton2_Callback(hObject,event data,handles)

close

3 基于GUI的分析

界面设计好以后，即可进行程序运行。点击“运行”，单击“分析”按钮，依次调用3个输入对话框，如图3所示，分别输入R、L、C的值(R=2，L=1，C=4，U0=2；R=2，L=0.5，C=0.5，U0=2；R=2，L=4，C=0.4，U0=2)，在对应的坐标轴中绘制过阻尼、临界和欠阻尼响应曲线，如图4所示。

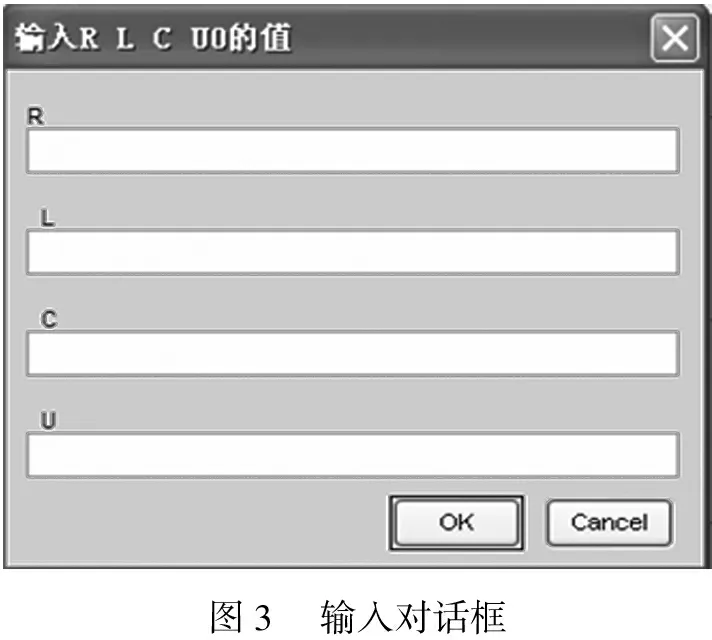
图3 输入对话框

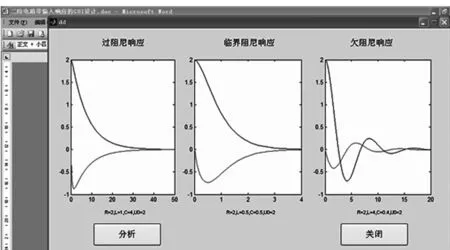
图4 响应波形

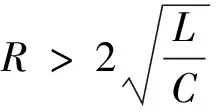
4 结束语

对电路动态响应的研究具有重要的实际意义，因为我们有时需要采取相应的措施以避免电路在动态过程中产生过电压、过电流现象，而有时又需要利用动态过程达到某种技术目的。在分析二阶电路的零输入响应时，利用MATLAB设计的GUI可以输入不同的R、L、C值并实时观察对应的放电波形，这样具有直观性。既可以让“教”者节省绘图和分析时间，又可让“学”者能通过改变输入值而改变输入波形，更具有直观性，同时，利用GUI提供的良好的人机对话可以避免枯燥的理论分析，提高学习兴趣，让学生在学习电类专业基础知识的同时，学习计算机软件知识。

参考文献：

[1]陈光，毛涛涛，王正林，等.精通MATLAB GUI设计[M].2版.北京:电子工业出版社，2011：219-271

[2]石生.电路基本分析[M].3版.北京:高等教育出版社，2008：228-265

[3]冯巧红.二阶电路的动态响应分析与仿真[J].滁州学院学报，2012(2)：42-44

[4]蔺红，樊艳芳.二阶电路的MATLAB仿真[J].新疆大学学报：自然科学版，2004(1)：65-68

[5]李树燕.电路基础[M].2版.北京.高等教育出版社，1994：478-487

[6]田敏，李江全，邓红涛，等.案例解说MATLAB典型控制应用[M].北京：电子工业出版社，2010：28-34

[7]朱明扬.RLC串并联稳态电路的MATLAB界面设计[J].东北电力大学学报，2009(4):21-25

[8]刘洋，杨薇，张付杰.二阶系统性能改善的MATLAB仿真分析[J].现代电子技术，2012(12)：98-100

[9]罗志娟，刘敏，易图林，等.基于MATLAB的RC串联电路暂态过程仿真[J].大学物理实验，2012(4)：105-107