镍铜合金NCu30-4-2-1电渣熔铸件的热变形行为
刘德林,陶春虎,关文秀,姜 涛,张 兵
(北京航空材料研究院 航空材料检测与评价北京市重点实验室,北京 100095)
蒙乃尔合金是以Ni为基的Ni-Cu合金,最早由美国国际镍公司开发,其典型成分为 70%Ni和30%Cu(质量分数),这是镍基耐蚀合金中应用最广泛的合金[1−2]。镍铜合金NCu30-4-2-1是Ni-Cu-Si-Fe-Mn系弥散硬化型高耐磨性Ni基合金,通常称为含硅蒙乃尔合金,该合金属于沉淀硬化型,即通过合适的热处理能够使Si以金属间化合物Ni3Si相形式从基体中析出,在晶界和晶粒内呈弥散分布,大大提高合金的强度和硬度。与其他蒙乃尔合金相比,NCu30-4-2-1由于硅含量较高(质量分数为4%),具有高硬度、高强度、优良的耐磨性和抗粘合性的特点,因而适合用于制造航空燃油装置及其他要求工作稳定的精密摩擦件[3−4]。该合金不能进行热处理强化,主要是通过固溶强化和热加工工艺来提高合金的力学性能。研究表明[5],该合金挤压态的塑性较铸态有较大提高。采用普通铸造工艺制备的镍铜合金NCu30-4-2-1铸棒心部不可避免存在缩孔等铸造缺陷,而且由于正向挤压成形时坯料心部的变形量小于表面的变形量,从而挤压成形后挤压棒心部仍存在原始铸造缺陷,导致心部材料的塑性较差,满足不了使用要求。而采用电渣熔铸工艺制备的NCu30-4-2-1铸件具有纯净度高、组织致密、成分均匀等优点,可改善挤压制品的力学性能。ZHOU等[6]对镍铜合金 NCu30-4-2-1摩擦磨损特性的研究表明:铸态合金的摩擦磨损性能较差;YANG等[7]对硅在该合金中的行为进行了研究。然而,目前尚未见关于NCu30-4-2-1电渣熔铸件热变形行为的研究报道。为此,本文作者对镍铜合金NCu30-4-2-1电渣熔铸件进行等温压缩实验,研究该合金的热变形流变应力行为及显微组织演化规律,为制定与优化该合金的热挤压工艺提供理论依据。
1 实验
1.1 实验材料
本实验所用的镍铜合金NCu30-4-2-1是由北京航空材料研究院制备的电渣重熔铸棒,其化学成分(质量分数)如下:Cu 29.0%~31.0%,Si 3.8%~4.5%,Fe 1.5%~2.5%,Mn 0.8%~1.5%,C不大于0.2%,Al不大于0.30%,Mg不大于0.10%,S不大于0.02%。沿铸棒轴向切取d 10 mm×15 mm的圆柱试样。
1.2 实验方法
将加工好的试样在Gleeble−3800热模拟机上进行等温压缩实验,压缩变形温度为900~1 100 ℃,应变速率为0.01~10 s−1,压缩率为60%。压缩变形前保温5 min,压缩时试样两端粘贴润滑剂片,变形后立即对试样进行水淬,以保留其高温变形组织,水淬延迟时间约为1 s。采用Gleeble−3800热模拟机的计算机系统自动采集应力、应变、位移、温度及时间等数据。将热压缩后的试样在中间垂直上下表面切开,采用OLYMPUS PME3型光学显微镜观察合金压缩变形后的金相组织。
2 结果与讨论
2.1 真应力—真应变曲线
图1所示为镍铜合金NCu30-4-2-1在高温等温压缩变形的真应力—真应变曲线。由图1可见,在变形温度900~1 100 ℃和应变速率为0.01~10 s−1的条件下,流变应力随应变量的增加而迅速升高,达到峰值后铸件下降至稳态值,进入稳态变形阶段。该现象是由于合金在塑性变形过程中,加工硬化和动态软化同时进行。在变形初期,外加应力使位错密度增加,位错间的交互作用增大了位错运动的阻力,交滑移引起的软化不足以克服位错密度增加带来的硬化,因此,在峰值应力之前加工硬化处于主导地位,应力水平迅速上升;随着应变量的增加,晶内储存能逐渐增加,动态软化与加工硬化达到动态平衡,流变应力基本不变[8]。
从图1还可以看出,在同一应变速率下,流变应力随温度的升高明显下降,这是由于随着温度的升高,热激活作用增加,原子动能增加,位错运动的阻力下降,空位和间隙原子等点缺陷也更加活跃,因而产生动态回复及动态再结晶引起的软化程度也随温度的升高而增大,导致合金的流变应力降低。在同一温度下,该合金的流变应力随应变速率的增加而增大,说明该合金是正应变速率敏感材料。
2.2 流变应力方程
在热变形过程中,材料在任何应变或稳态下的高温流变应力σ强烈地取决于变形温度 T和应变速率,通常可采用SELLARS和MCTEGART[9]提出的双曲正弦形式加以描述:

式中:)(σF为应力的函数,在不同的条件下分别可以表示为以下3种形式:
ασ<0.8时,

ασ>1.2时,

所有应力下,

对所有应力状态,式(1)可表示为
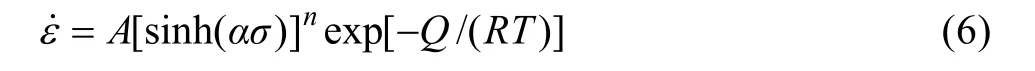

式中:α、n、A、β为常数,α为应力水平参数(mm2·N−1),n 为应力指数,A 为结构因子(s−1),Q 为热激活能,是材料在热变形过程中重要的力学性能参数,反映材料热变形的难易程度;T为绝对温度;R为摩尔气体常数;为应变速率。求出α、n、A、Q,即可描述材料的高温流变特性。大量的研究结果表明[10−12],式(6)能较好地描述压缩、挤压、扭转等常规的热加工变形。
另外,SELLARS和TEGART提出并用实验验证了热变形条件通常可用温度补偿的应变速率因子Zener-Hollomon参数Z来描述[9,13]:

研究表明,在低应力水平下,流变应力σ和Z可用指数关系描述,而在高应力水平下可以幂指数关系描述,在整个应力水平下可用双曲函数关系描述。实际上,式(7)在形式上与式(6)是一致的。
对式(2)和(3)两边取对数:
ασ<0.8时,

ασ>1.2时,

由式(6)可得:

考虑到峰值应力均出现在应变较小的时刻,温升修正前后峰值变化并不明显,为方便计算,取相应、T条件下的真实峰值应力,分别以σln和ln 为坐标作图,结果如图2所示。由式(8)可知,直线ln—σln斜率,设为n1;由式(9)可知,直线ln —σ的斜率,设为β。采用最小二乘法线性回归,n1取图2(a)中峰值应力较低的3条直线(即变形温度为1 000、1 050和1 100 ℃)斜率的平均值;β取图2(b)中峰值应力较高的3条直线(即变形温度为900、950和1 000 ℃)斜率的平均值;α可以通过式(5)求出。计算得到n/βα==0.005 026。
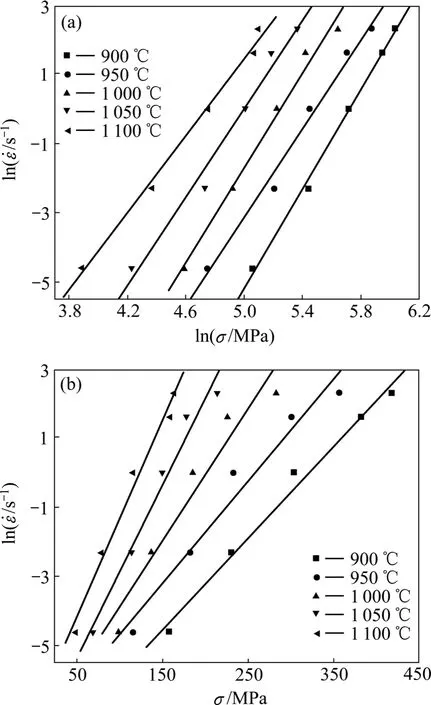
图2 不同变形温度下应变速率和流变应力之间的关系Fig.2 Relationship between strain rate and flow stress at different deformation temperatures∶ (a) ln—lnσ; (b)ln—σ

取峰值应力和对应温度值,并将以上得出的α值代入式(11),绘制 ln[sinh(ασ) ]— ln图,n2为直线ln[sinh(ασ) ]— ln的斜率。采用最小二乘法线性回归,得n2= 4.754 952;再将n2值代入式(5)得到一个调整后的α′值,α′=β/n2=0.006 109,将调整后的α′值重新代入式(11)和(12),绘制相应的 ln[sinh(ασ)]— ln图以及 ln[sinh(ασ)]—103T−1图,如图3和4所示。采用最小二乘法线性回归,n3值取图3中1 000、950和900 ℃这3条直线斜率的平均值,得到调整后的n3=4.462 888;k为直线 ln[sinh(ασ)]—T−1的斜率,k值取图4中 5条直线斜率的平均值(1.462 364),则Q=Rnk=527.5 kJ/mol。重复上述步骤,直至Q值变化不大时视为精确值。计算10次后,Q值基本趋于稳定值,Q=416.5 kJ/mol。

图3 不同变形温度下流变应力与应变速率的关系Fig.3 Relationship between flow stress and strain rate at different deformation temperatures
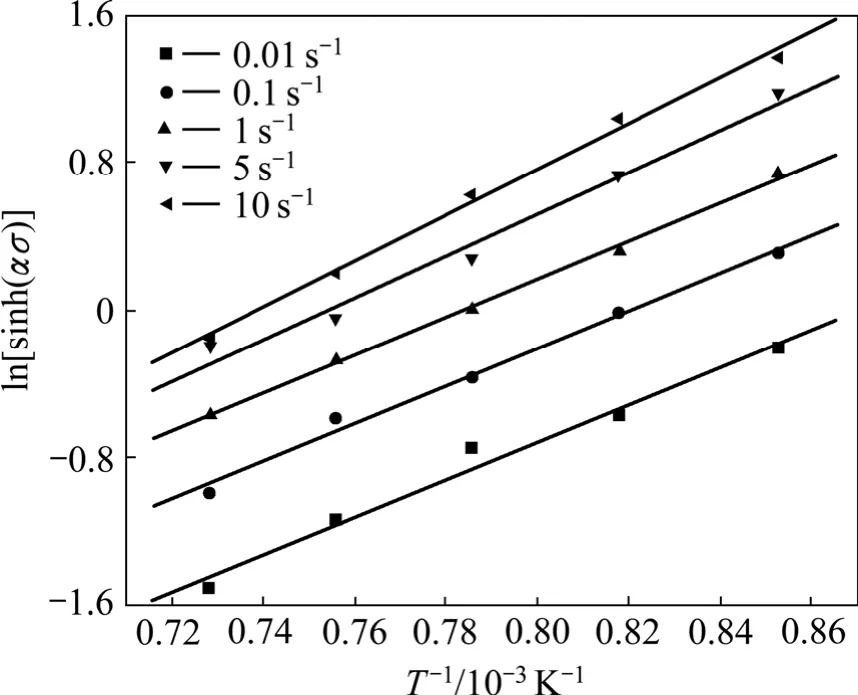
图4 不同应变速率下流变应力与变形温度的关系Fig.4 Relationship between flow stress and deformation temperatures at different strain rates
对式(7)求对数得:

由)(σF的其他2种形式即式(2)、(3),式(7)可表示如下:

分别对式(14)和(15)求对数得:

将以上求得的Q值及不同的应变速率和变形温度代入式(13),求得对应的lnZ值。将lnZ值和对应的σ值分别代入式(14)、(17)和(18)绘制ln Z—ln[sinh(ασ)]、lnZ—lnσ和lnZ—σ曲线,采用最小二乘法进行线性回归,结果如图5所示。图中 ln Z—ln[sinh(ασ)]、lnZ—lnσ、lnZ—σ关系曲线的线性相关系数分别为0.988 21、0.993 43和0.968 41,可见相比较而言,lnZ—lnσ较好地满足线性关系,将图5(b)中的斜率和截距代入式(17)得到 lnA1=6.477 08,n=6.299 87,将其代入式(1)可得合金的流变应力方程如下:
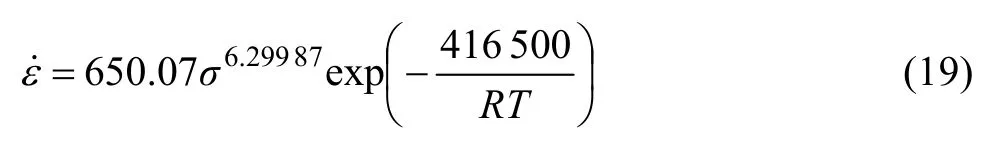
2.3 高温压缩过程中显微组织的演化规律
图6所示为不同变形条件下合金的金相显微组织,可见在变形温度为900 ℃、应变速率为0.01 s−1条件下,在变形的晶粒界面出现了一些细小的晶核(见图6(a)中箭头所指),这些晶核即为再结晶晶核;而在变形温度为900 ℃、应变速率为1 s−1的条件下,很难观察到再结晶晶核(见图6(b))。这是由于塑性变形需要一定的时间来进行,应变速率高时,变形时间短,使得动态再结晶还来不及充分发生[14−15]。在应变速率为0.01 s−1、变形温度为950 ℃和1 000 ℃条件下,再结晶晶粒逐渐增多(图6(c)和(d)),但在变形温度为 1 000 ℃时,仍存在少部分未发生再结晶的变形晶粒(图6(d)中箭头所指)。当合金在1 050 ℃变形,此时已发生了完全再结晶,变形晶粒全部由等轴的再结晶晶粒所代替,在应变速率为1 s−1时,晶粒比较细小、均匀(图6(e))。随着温度进一步升高,当变形温度为1 100 ℃时,再结晶晶粒尺寸增大(图6(f)),表明此时处于晶粒长大阶段。

图5 Z参数与流变应力之间的关系Fig.5 Relationship between flow stress and Zener-Hollomon parameter∶ (a) ln Z— ln[sinh(ασ) ]; (b) ln Z—lnσ ; (c) ln Z—σ

图6 不同变形条件下合金的显微组织Fig.6 Microstructures of specimens after being compressed under different conditions∶ (a)900 ℃, 0.01 s−1; (b)900 ℃, 1 s−1;(c)950 ℃, 0.01 s−1; (d)1 000 ℃, 0.01 s−1; (e)1 050 ℃, 1 s−1; (f)1 100 ℃, 1 s−1
3 结论
1)镍铜合金NCu30-4-2-1高温压缩变形时的流变应力随温度的升高而减小,随应变速率的增加而增大。流变应力σ与变形温度T与应变速率之间满足关系其中,变形激活能Q=416.5 kJ/mol。
2)镍铜合金NCu30-4-2-1高温压缩变形时的显微组织受变形温度和应变速率的影响,温度越高、应变速率越低,越有利于动态再结晶的发生。在变形温度为1 050 ℃、应变速率为1 s−1的条件下,合金发生了完全动态再结晶,晶粒细小、均匀。
[1]PARK K H, MOHAPATRA D, RAMACHANDRA REDDY B.A study on the oxidative ammonia/ammonium sulphate leaching of a complex (Ni-Cu-Co-Fe)matte[J].Hydrometallurgy, 2007, 86∶164−171.
[2]YE Tang, HU Chuan-shun, QIN Hua, ZHU Jian.Study of corrosion behavior of Monel 400 alloy[J].Material & Heat Treatment, 2006, 35(22)∶ 36−38.
[3]GOUDA V K, SELIM I Z, HEDR A A K.Pitting corrosion behavior of Monel-400 alloy in chloride solutions[J].J Mater Sci Technol, 1999, 15(3)∶ 208−212.
[4]SINGH V B, GUPTA A.The electrochemical corrosion and passivation behavior of Monel 400 in concentrated acids and their mixtures[J].Journal of Materials Science, 2001, 36∶1433−1442.
[5]GUO Tong-xiu, LIU De-lin, YU Yang.Preparation of high silicon nickel-copper alloy NCu30-4-2-1 extrusion bars[J].Journal of Materials Engineering, 2009, 2∶ 24−28.
[6]ZHOU Yong-xin, LU Zhen-lin, ZHANG Min, ZHAO Xi-cheng,FAN Zhi-kang.Study on the tribological behavior of Monel alloy[J].Ordnance Material Science and Engineering, 2004,27(5)∶ 24−27.
[7]YANG Zhi-jun, LI Xian-min, WANG Zeng-min, LI Lin.Investigation on the behavior of silicon in Ni-Cu-Fe-Mn-Si alloy[J].Rare Metals and Engineering, 1997, 26(5)∶ 47−50.
[8]KOU Lin-yuan, JIN Neng-ping, ZHANG Hui, HAN Yi, WU Wen-xiang, LI Luo-xing.Flow stress behavior of 7150 aluminum alloy during hot compression deformation at elevated temperature[J].The Chinese Journal of Nonferrous Metals, 2010,20(1)∶ 44−46.
[9]SELLARS C M, MCTEGART W J.On the mechanism of hot deformation[J].Acta Metal, 1966, 14∶ 1136−1138.
[10]MCQUEEN H J, YUE S, RYAN N D, FRY E.Hot working characteristics of steels in austenitic state[J].J Mater Process Technology, 1995, 53(1)∶ 293−310.
[11]MCQUEEN H J, FRY E, BELLING J.Comparative constitutive constants for hot working of Al-4.4Mg-0.7Mn (AA5083)[J].Journal of Materials Engineering and Performance, 2001, 10(2)∶164−172.
[12]HU Hui-e, YANG Li, ZHEN Liang, SHAO Wen-zhu, ZHANG Bao-you.Relationship between boundary misorientation angle and true strain during high temperature deformation of 7050 aluminum alloy[J].Transactions of Nonferrous Metals Society of China, 2008, 18(4)∶ 795−798.
[13]ZENER C, HOLLOMON J H.Effect of strain-rate upon the plastic flow of steel[J].J Appl Phys, 1944, 15(1)∶ 22−27.
[14]BLUM W, ZHOU Q, MERKEL R, MCQUEEN H J.Geometric dynamic recystallization in hot torsion of Al-5Mg-0.6Mn[J].Mater Sci and Eng A, 2002, 205∶ 23−30.
[15]DOHERTY R D, HUGHES D A, HUMPHRYS F J.Current issues in recystallization∶ A review[J].Mater Sci and Eng A,1997, 238∶ 217−274.

