岩爆烈度预测的改进物元可拓模型与实例分析

胡建华 ，尚俊龙 ，周科平

(1.中南大学 资源与安全工程学院，长沙 410083；2.中南大学 湖南省深部资源开发与灾害控制重点实验室，长沙 410083)

岩爆是高地应力区的地下工程在开挖过程中或开挖完毕后，围岩因开挖卸荷发生脆性破坏而导致储存于岩体中的弹性应变能突然释放且产生爆裂松脱、剥落、弹射甚至抛掷现象的一种动力失稳地质灾害[1]。岩爆发生，通常会给地下工程如矿山、公路、铁路、核电等领域带来一定的经济损失，甚者带来灾难性后果[2−4]。如美国Lucky Friday煤矿开采深度达2 000 m以上，每年因岩爆减产造成经济损失50多万美元；南非典型深部金矿Wester金矿，在一具体统计时间内因岩爆造成的员工死亡率为 0.1%/a，占矿山死亡率的46%；辽宁红透山铜矿矿体埋深1 047 m，1995—2004年矿山岩爆监测记录达49次，岩爆的形式主要为岩块弹射、坑道片帮、顶板冒落等。因此，为减少岩爆带来的破坏，降低对工程施工人员、设备的威胁，岩爆的烈度分级预测就显得尤为重要。

自1738年英国来比锡煤矿首次发生岩爆以来，国内外学者从不同角度对岩爆分级预测问题进行了探讨，如 FUJII等[5]基于矿岩微裂隙，对三维弹性应力进行分析，实现了岩爆的预测；WANG和PARK[6]提出岩体中应变能的积累是影响岩爆发生与否的关键因素之一，并借助数值分析模型来分析应变能，对岩爆进行了预测；陈秀铜和李璐[7]将系统工程决策方法和模糊数学评价方法有机结合，提出了层次分析法−模糊数学(AHP-FUZZY)岩爆综合预测方法；文畅平[8]应用属性数学理论，建立了岩爆发生预测和烈度分级的属性识别模型；祝云华等[9]建立一种基于改进支持向量机算法的岩爆预测方法；谢学斌和潘长良[10]将岩爆与其影响因素之间的关系作为灰色系统，提出采用灰类白化权函数聚类的预测方法对岩爆灾害进行预测；宫凤强等[11]建立了隧道岩爆预测的距离判别分析模型；陈海军等[12]建立了岩爆预测的人工神经网络模型；付玉华和董陇军[13]将Bayes判别理论应用到深部硬岩岩爆预测中；周科平和古德生[14]建立基于GIS的岩爆倾向性模糊自组织神经网络分析模型。以上预测岩爆的理论方法均从不同的角度对岩爆进行预测，并取得了一定的预测效果。由于岩爆的空间分布规律和时间分布规律都十分复杂，需要多种方法结合和途径的互补才能达到准确预测岩爆烈度的目的。

物元可拓方法[15]是用形式化的工具，从定性和定量两个角度去研究解决矛盾问题的规律和方法。目前可拓理论已在综合评价[15−17]和决策[17−19]等领域得到应用，但其理论方面还有一些不完善之处，比如在使用过程中可能出现待评物元特征值超出节域范围和权重分配不合理等问题，导致评价过程具有局限性。本文作者在前人研究的基础之上，提出岩爆烈度分级预测的改进物元可拓模型。首先通过求解隶属函数，将节域范围进行归一化处理，解决待评物元特征值超出节域问题；其次引入博弈理论，将客观动态权重与主观静态权重优化融合得到综合权重，克服了传统物元可拓评价方法只依赖指标客观权重，而忽略指标本身对评价问题的重要差异性的缺陷。

1 岩爆烈度预测的改进物元可拓模型

物元可拓法是20世纪80年代初由我国蔡文[20]提出的，主要是利用物元理论分析与事物相关的多个因素，利用关联函数建立可拓矩阵并进行可拓聚类分析，在此基础上建立物元可拓模型。岩爆烈度分级是一个十分复杂的多指标特征参数的综合评价问题，而物元可拓理论正能解决此类复杂问题，其主要是利用可拓评价的思想，建立岩爆烈度多指标特征参数评价模型并以定量的数值给出评定结果，能够完整的反映事物的综合水平。

改进物元可拓模型的基本思路：1)基于隶属函数，将岩爆评价标准及待评岩体指标参量进行规格化处理，得到节域的隶属化范围，解决待评物元特征值超出节域问题；2)引入博弈论，将客观动态权重与主观静态权重优化融合得到综合权重，弥补传统物元可拓评价方法只依赖指标客观权重，而忽略指标本身对评价问题的重要性差异的缺陷。岩爆烈度预测的改进物元可拓流程见图1。

物元可拓理论已在工程等领域有着广泛的应用，限于篇幅，物元可拓理论基本概念及矩阵形式参见文献[15−19]。

1.1 基于隶属函数的岩爆评价指标规格化

正如文献[16]所述，若待评物元的特征值超出节域范围，就会使关联函数失效，无法计算综合关联度，因此需要对物元可拓方法进行改进。蔡文等[20]通过修正关联函数表达形式对此问题进行了深入的探讨，但求解过程比较繁琐。本文作者提出选用线性法量纲法[21]来解决此类问题，计算公式如下：

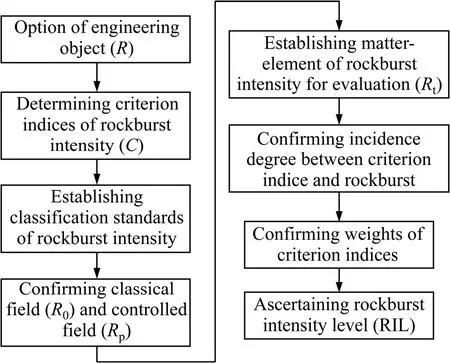
图1 岩爆烈度预测改进物元可拓流程Fig.1 Flow chat of classification forecasting of rockburst intensity with improved matter-element extension method

效益型即越大越优的指标∶

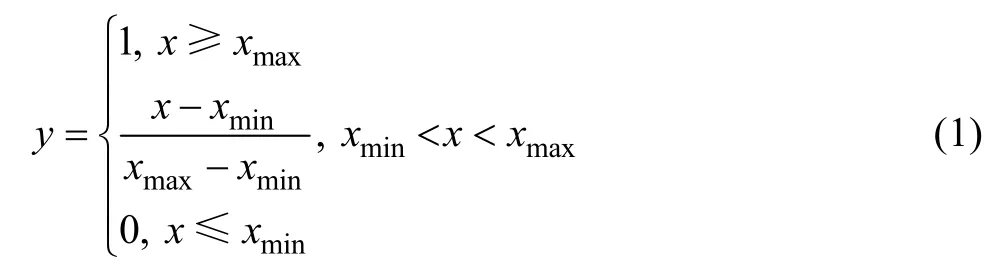
成本型即越小越优的指标∶

式中：x为待评物元特征值大小；xmax和xmin分别为评价标准最大和最小值。

从本质上讲，指标无量纲化过程即是求解隶属函数的过程，无量纲化公式即是隶属函数。通过隶属函数(1)、(2)分对经典域、节域、待判物元及岩爆烈度等级标准进行无量纲化处理，能够方便、快捷地解决关联函数失效问题。

1.2 基于博弈论的指标综合赋权

传统的物元可拓评价模型在确定指标权重方时，通常采用的方法有层次分析法、熵权法、简单关联函数法、专家调查法等。这些方法要么存在较大的主观因素，要么没有考虑指标本身对评价问题的重要性差异。通常在实际评价问题中，评价指标的重要程度是客观存在的，并受到决策者主观意愿的影响，只有主客观综合权重才能完全反映指标重要程度，然而在现有文献中[22]，一般是通过线性加权法来综合考虑主客观权重对结果的影响，其中偏好系数u一般都是根据决策者来选取，从而带来很大的主观随意性，这是不科学的。鉴于此，本文作者基于博弈论[23]，将用简单关联函数(具体步骤参见文献[24])得到的客观动态权重与用专家打分法得到的主观静态权重优化、融合，从而得到岩爆烈度分级指标的综合权重。基于博弈论的综合赋权方法具体步骤如下：

对于多指标评价问题，为了更加科学合理的对指标进行赋权，可以使用L(本研究中L=2)中不同的方法分别得到各评价指标权重，由此构造一个基本权重集uk={uk1，uk2，…，ukm}，k=1，2，…，L，本文作者记这L个权重向量uk的任意线性组合为

“我用的是手动模式，但是我忘记调高快门速度了，所以这幅作品比我想要的效果模糊了些。我记得当时的快门速度是1/100秒，而最后成片的效果是这样的，可以说这台相机的稳定性和整体清晰度很惊人了。”

为了在可能权重集中选出一个最满意的权重uk*，将式(3)L个线性组合系数 αk进行优化，目标是使 u与各个uk的离差极小化。由此可以推导出下面的对策模型：

依据矩阵微分性质，式(4)最优化一阶导数条件为下面线性方程组：

运用 Matlab 计算得到(α1，α2，…，αL)，通过归一化处理，可得

则评价指标综合权重为

1.3 确定岩爆烈度等级

设第i个工程对象Ni的第k个岩爆烈度评价指标关于岩爆等级j的关联函数为

式中：vik为第i个工程对象对应的第k个岩爆烈度评价指标，v0jk≤a0jk，b0jk＞岩爆等级 j第 k个特征对应的值域，a0jk和b0jk分别为值域的下限和上限，akp≤mkp，nkp＞P关于特征值所取的量值范围。

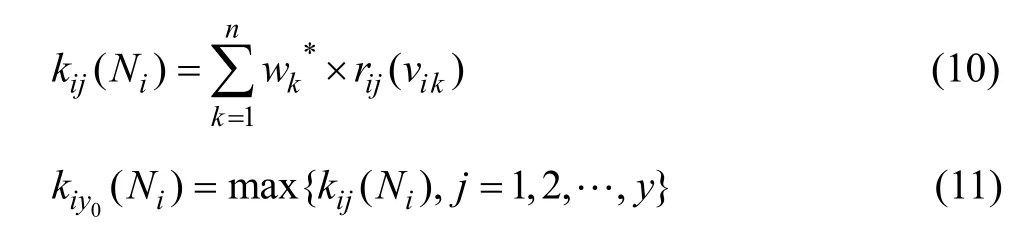
式中：Kiy0(Ni)表明工程Ni关于岩爆等级j的最大关联度，即工程Ni所对应岩爆等级的关联程度。

根据式(14)最大关联度准则，可以判定工程对象Ni所属的岩爆烈度等级为第y0级。

2 实例分析

为验证改进的物元可拓模型的正确性和有效性，参考国内外若干大型地下工程实测岩爆资料[10,12,17,25],见表1。按照图1岩爆烈度分级步骤，将建立的改进物元可拓模型应用于实际工程岩爆烈度预测。

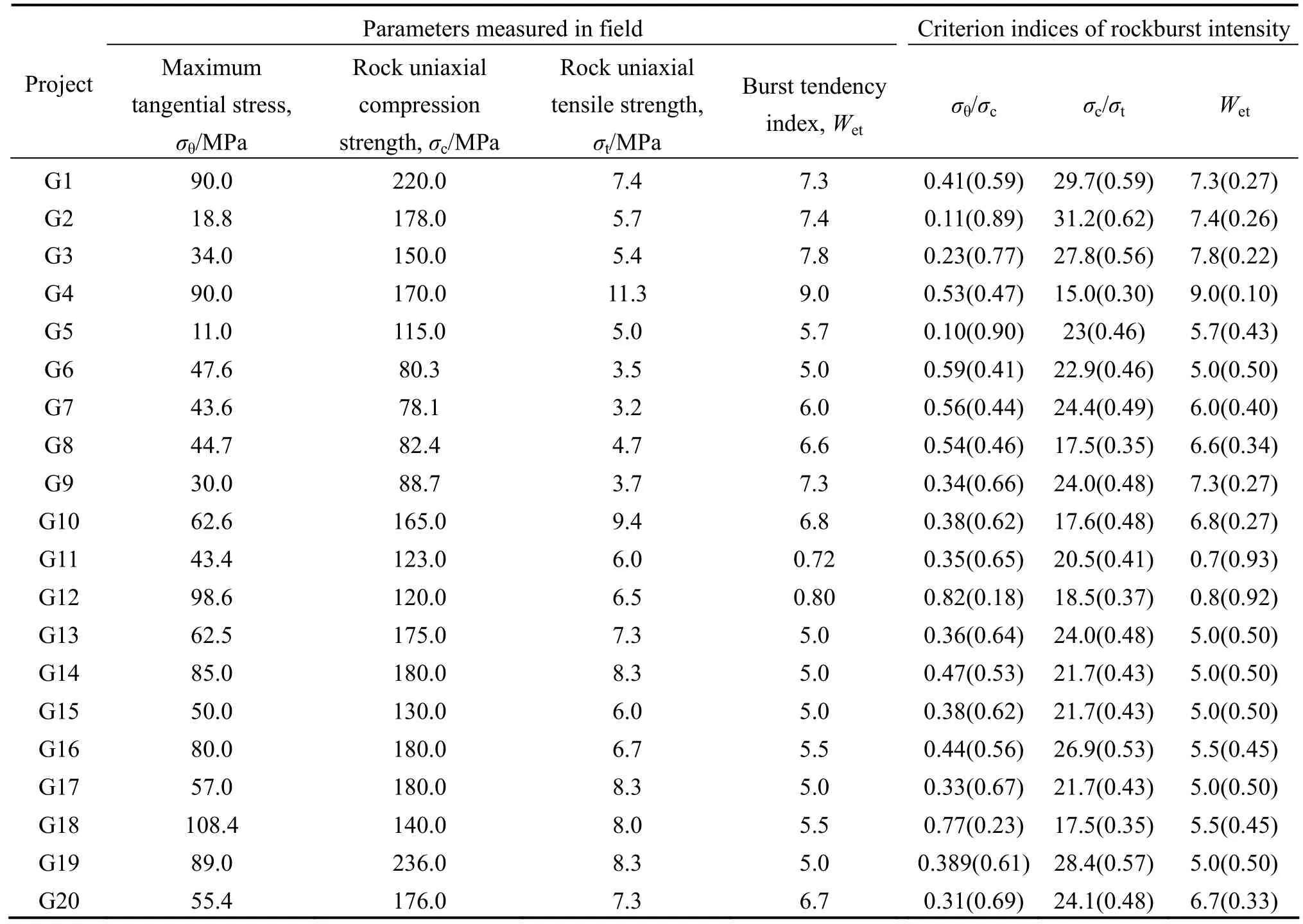
表1 国内外若干工程岩爆分析初始数据Table 1 Basic data for rockburst intensity analysis of some projects at home and abroad

2.1 确定岩爆烈度分级指标及分级标准隶属度

由于岩爆烈度受诸多因素影响，且不同学者提出的评价方法的指标也不尽相同，参考相关岩爆烈度分级研究结果[7−13,17,20]，从3个不同侧面选择岩爆烈度分级指标，即1)σθ/σc：硐室最大切向应力与岩石单轴抗压强度之比，比值越大则岩爆烈度越大(越小越好，成本型指标)；2)σc/σt：岩石单轴抗压强度与岩石单轴抗拉强度之比，比值越小则岩爆烈度越大(越大越好，效益型指标)；3)Wet：冲击倾向指数，其值越大，岩爆发生时放出的能量越多，烈度越大(越小越好，成本型指标)。 并将岩爆烈度分为无岩爆(N01)、弱岩爆(N02)、中等岩爆(N03)和强岩爆(N04)几个级别。表2所列为岩爆烈度等级与分级指标对应关系。

2.2 岩爆烈度物元经典域R0、节域Rp及待评物元Rt

据表2，选择表中不同岩爆烈度等级的隶属范围作为经典域，3个岩爆烈度分级指标分别即做 c1～c3,建立的经典域物元如下：

依据表2中岩爆烈度分级指标的整体取值隶属范围确定节域：

依据表3确定20个工程实例待评物元，限于篇幅只列出前2个，见以下各式：

2.3 确定岩爆烈度评价指标与烈度等级关联度

根据式(7)，以G1工程为例来计算其特征c1的特征值v11关于Ⅰ、Ⅱ岩爆烈度等级的关联度，其余计算结果见表3。

因为v11(0.59)∉v011(0.7～1.0)，所以v11关于第Ⅰ等级的关联度为

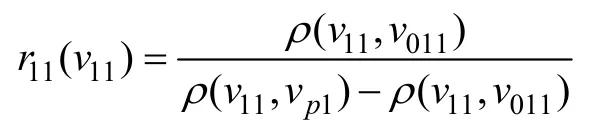
表2 岩爆烈度分级标准Table 2 Classification standards of rockburst intensity

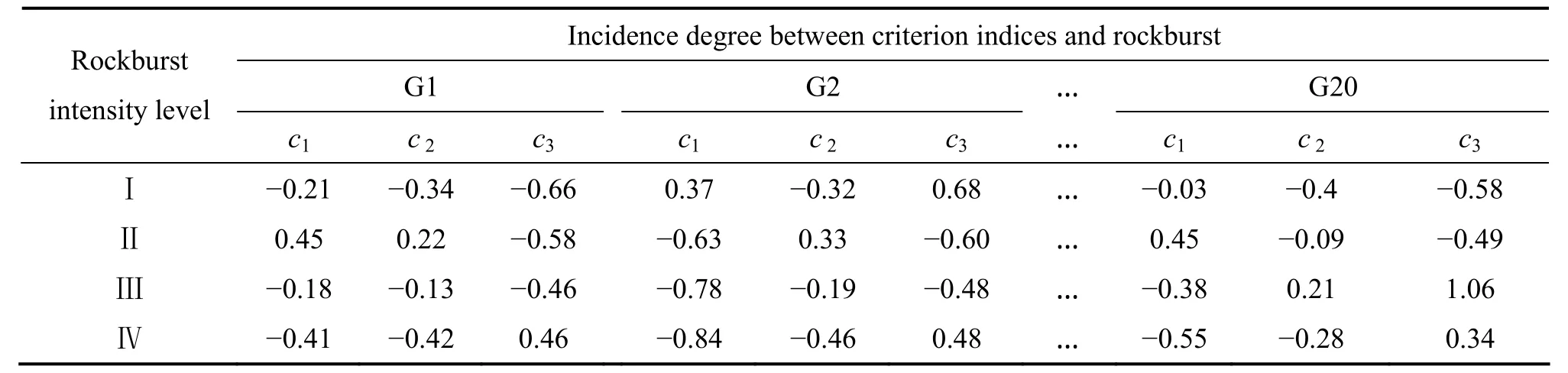
表3 特征值与岩爆烈度等级关联度Table 3 Relational degree of eigenvalue of evaluating indicators

而 v11(0.59)∈v021(0.5～0.7)，所以 v11对第Ⅱ等级的关联度为

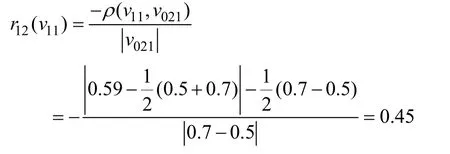
2.4 基于博弈论的评价指标赋权

从安全的角度考虑，岩爆评价指标值(特征值)落入级别越大，则岩爆发生烈度越大，因此，应赋予越大的权重。运用文献[25]简单关联函数，确定评价指标客观动态权重(特征值权重)；采用专家打分法得到各指标的主观静态权重，其中 σθ/σc为 0.3，σc/σt为 0.4，Wet为0.3。在充分考虑客观具体数值对结果的影响程度及指标本身含义的基础之上，通过博弈论将客观动态权重与主观静态权重优化、融合，最终得到综合权重。限于篇幅，在此只列出部分工程对象各指标权重计算结果，见表4。

2.5 岩爆烈度预测结果

通过第2.3节计算的关联度和第2.4节计算的指标综合权重，可以计算出评价对象与岩爆烈度等级综合关联度，如图2所示。根据最大关联度准则，可以得到20个工程对象岩爆烈度等级，并将预测结果与实际结果进行对比分析，见表5。从表5可以看出，预测结果与实际情况吻合较好，仅 G8岩爆烈度误判为Ⅲ级别(实际工程为Ⅱ级)，与文献[17]可拓综合评价方法预测结果及文献[20]模糊综合评判方法预测结果相比，本研究方法具有更好的预测准确度。并且改进的物元可拓模型克服传统物元可拓模型在待评物元特征值超出节域范围时无法计算的局限性，同时本研究将主客观权重进行博弈优化融合，使得权重的选取更加科学合理，使预测结果更加可靠。由此可见，改进的物元可拓模型用于岩爆烈度预测切实可行并且能提高准确度。

表4 评价指标权重值Table 4 Weight values of evaluating indicators

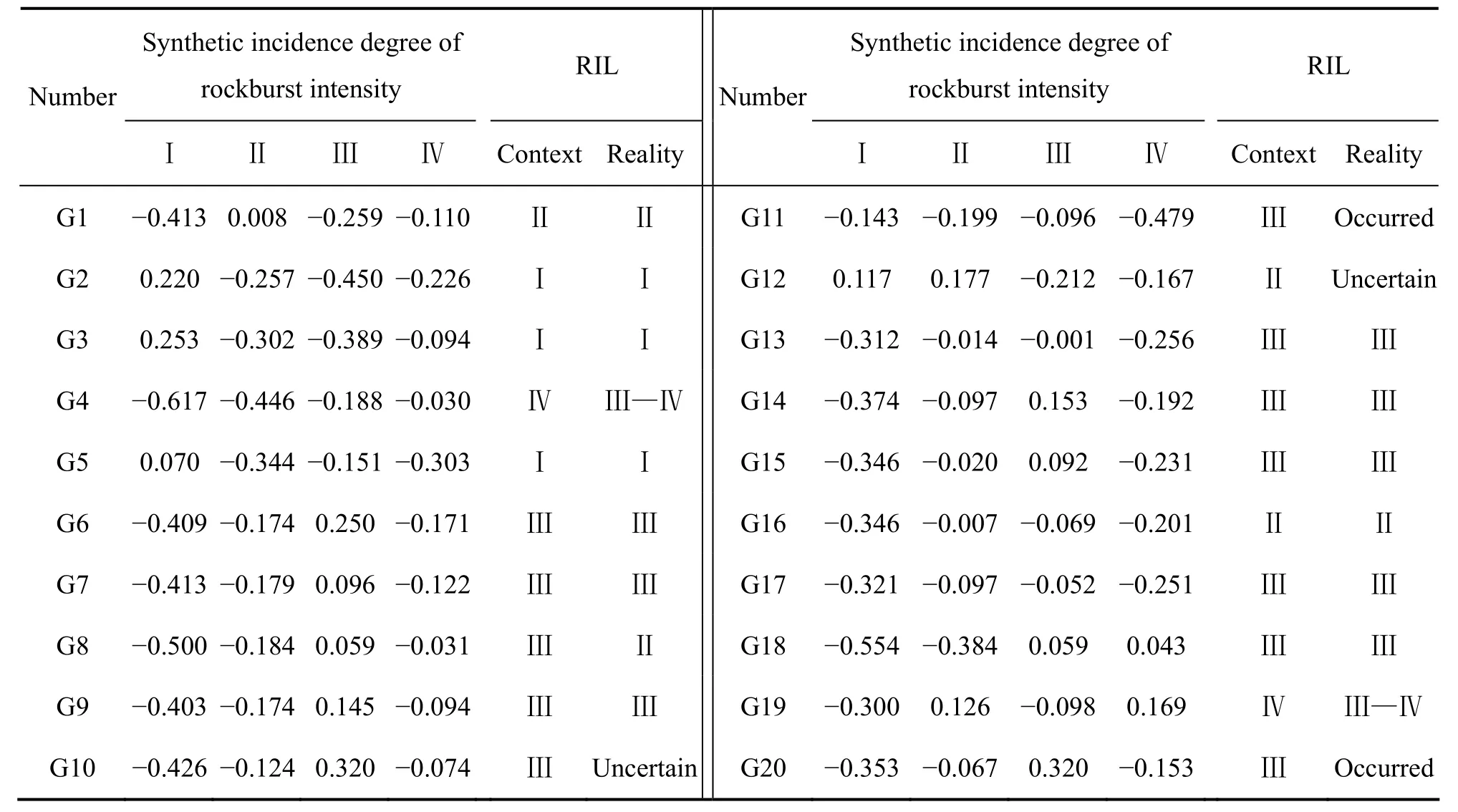
表5 岩爆烈度预测结果对比Table5 Comparison of practical situations results of proposed model

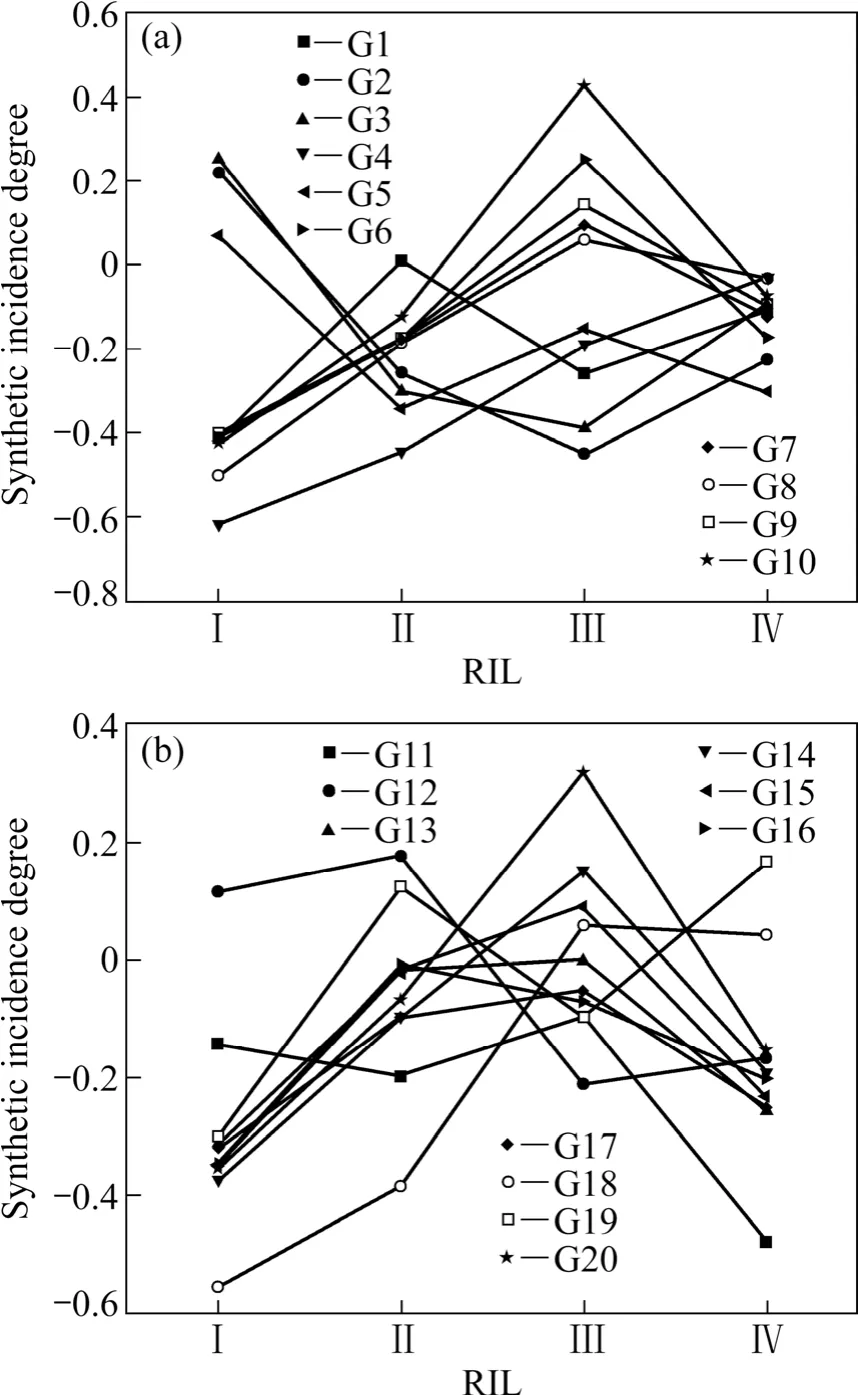
图2 工程样本岩的爆烈度等级Fig.2 Classification of rockburst intensity of engineering project examples

3 结论

1)综合考虑岩爆成因及特点，结合改进的物元可拓理论，建立了岩爆烈度预测的改进物元可拓模型。

2)该模型选取应力系数 σθ/σc，岩石脆性系数 σc/σt及弹性能量指数 Wet作为岩爆烈度分级的评价指标，运用隶属函数，对岩爆烈度分级标准进行隶属化，得到了节域隶属化范围，弥补待评物元指标值可能超出节域而使关联函数失效的缺陷；结合博弈论，优化融合评价指标客观动态权重与主观静态权重，得到指标综合权重。通过计算待评对象与岩爆烈度等级的综合关联度，并依据最大关联度准则确定岩爆烈度等级。

3)建立的岩爆烈度预测的改进物元可拓预测模型更加科学合理，预测结果与工程实际吻合较好，预测精度更高。

4)岩爆是一种十分复杂的动力失稳地质现象，对其发生及烈度准确预测难度较大。将改进的物元可拓方法运用于岩爆烈度预测问题中，建立岩爆烈度预测的改进物元可拓模型，可以对实际工程岩爆烈度等级进行预测，但该模型只能得到岩爆烈度的某一确切等级，难以对混合型及中间型岩爆做出预测，此问题有待于后续进一步的研究。

[1]吕 庆, 孙红月, 尚岳全, 陈侃福, 徐国峰.深埋特长公路隧道岩爆预测综合研究[J].岩石力学与工程学报, 2005, 24(16)∶2982−2988.LÜ Qing, SUN hong-yue, SHANG Yue-quan, CHEN Kan-fu,XU Guo-feng.Comprehensive study on prediction of rockburst in deep and over-length highway tunnel[J].Chinese Journal of Rock Mechanics and Engineering, 2005, 24(16)∶ 2982−2988.

[2]JESENAK P, KAISER P K, BRUMMER R K.Rockburst damage potential assessment[C]//Proceedings of the 3rd International Symposium on Rockburst and Seismicity in Mines.Kingston, Ontario, Canada∶ Balkema, Rotterdam, 1993∶ 81−87.

[3]SIMSER B, JOUGHIN W C, ORTLEPP W D.The performance of Brunswick Mines rockburst support system during a severe seismic episode[J].Journal of The South African Institute of Mining and Metallurgy, 2002, 102(5)∶ 217−223.

[4]王旭昭, 王洪勇, 曲金洪.红透山铜矿岩爆灾害特征及其地质条件分析[J].地质与勘探, 2005, 41(6)∶ 102−106.WANG Xu-zhao, WANG Hong-yong, QU Jin-hong.Characteristics of rockburst disaster and its geological conditions in the Hongtoushan copper mine[J].Geology and Prospecting, 2005,41(6)∶ 102−106.

[5]FUJII Y, ISHIJIMA Y, DEGUCHI G.Prediction of coal face rockbursts and microseismicity in deep longwall coal mining[J].Int J Rock Mech Min Sci, 1997, 34(1)∶ 85−96.

[6]WANG J A, PARK H D.Comprehensive prediction of rockburst based on analysis of strain energy in rocks[J].Tunnelling and Underground Space Technology, 2001, 41∶ 49−57.

[7]陈秀铜, 李 璐.基于 AHP-FUZZY方法的隧道岩爆预测[J].煤炭学报, 2008, 33(11)∶ 1230−1234.CHEN Xiu-tong, LI Lu.Prediction of tunnel rockburst based on AHP-FUZZY method[J].Journal of China Coal Society, 2008,33(11)∶ 1230−1234.

[8]文畅平.属性综合评价系统在岩爆发生和烈度分级中的应用[J].工程力学, 2008, 35(6)∶ 153−158.WEN Chang-ping.Application of attribute synthetic evaluation system in prediction of possibility and classification of rockburst[J].Engineering Mechanics, 2008, 35(6)∶ 153−158.

[9]祝云华, 刘新荣, 周军平.基于 v-SVR算法的岩爆预测分析[J].煤炭学报, 2008, 33(3)∶ 277−281.ZHU Yun-hua, LIU Xin-rong, ZHOU Jun-ping.Rockburst prediction analysis based on v-SVR algorithm[J].Journal of China Coal Society, 2008, 33(3)∶ 277−281.

[10]谢学斌, 潘长良.岩爆灾害的灰类白化权函数聚类预测方法[J].湖南大学学报∶ 自然科学版, 2007, 34(8)∶ 16−20.XIE Xue-bin, PAN Chang-liang.Rockburst prediction method based on grey whitenization weight function cluster theory[J].Journal of Hunan University∶ Natural Sciences, 2007, 34(8)∶16−20.

[11]宫凤强, 李夕兵, 林 杭.隧道岩爆预测的距离判别分析模型研究及应用[J].中国铁道科学, 2007, 28(4)∶ 25−28.GONG Feng-qiang, LI Xi-bing, LIN Hang.Model of distance discriminant analysis for rockburst prediction in tunnel engineering and its application[J].China Railway Science, 2007,28(4)∶ 25−28.

[12]陈海军, 郦能惠, 聂德新, 尚岳全.岩爆预测的人工神经网络模型[J].岩土工程学报, 2002, 24(2)∶ 229−232.CHEN Hai-jun, LI Neng-hui, NIE De-xin, SHANG Yue-quan.A model for prediction of rockburst by artificial neural network[J].Chinese Journal of Geotechnical Engineering, 2002, 24(2)∶229−232.

[13]付玉华, 董陇军.岩爆预测的Bayes判别模型机应用[J].中国矿业大学学报, 2009, 38(4)∶ 56−64.FU Chun-hua, DONG Long-jun.Bayes discriminant analysis model and its application to the prediction and classification of rockburst[J].Journal of China University of Mining and Technology, 2009, 38(4)∶ 56−64.

[14]周科平, 古德生.基于 GIS 的岩爆倾向性模糊自组织神经网络分析模型[J].岩石力学与工程学报, 2004, 23(18)∶ 56−64.ZHOU Ke-ping, GU De-sheng.Application of GIS based on neural network with FUZZY self-organization to assessment of rockburst tendency[J].Chinese Journal of Rock Mechanics and Engineering, 2004, 23(18)∶ 3093−3097.

[15]高 峰, 周科平, 胡建华.采场稳定性的模糊物元评价模型及应用研究[J].采矿与安全工程学报, 2006, 23(2)∶ 164−168.GAO Feng, ZHOU Ke-ping, HU Jian-hua.Fuzzy matter-element evaluation model for the stability of stope and its application[J].Journal of Mining & Safety Engineering, 2006, 23(2)∶ 164−168.[16]HE Yong-xiu, DAI Ai-ying, ZHU Jiang, HE Hai-ying, LI Fu-rong.Risk assessment of urban network planning in China based on the matter-element model and extension analysis[J].Electrical Power and Energy Systems, 2011, 33(3)∶ 775−782.

[17]陈 祥, 祈小博, 蔡新滨, 沈宇鹏.可拓综合评价方法在岩爆判别中的应用[J].北京交通大学学报, 2009, 33(1)∶ 99−108.CHEN Xiang, QI Xiao-bo, CAI Xin-bin, SHEN Yu-peng.Extensional evaluation method and its application in the judgments of rockburst[J].Journal of Beijing Jiaotong University, 2009, 33(1)∶ 99−108.

[18]邓红卫, 周科平, 高 峰, 陈庆发.矿岩可崩性的可拓聚类预测研究[J].中国安全科学学报, 2008, 18(1)∶ 34−39.DENG Hong-wei, ZHOU Ke-ping, GAO Feng, CHEN Qing-fa.Study on extension cluster prediction for ore rock cavability[J].China Safety Science Journal, 2008, 18(1)∶ 34−39.

[19]JUN Ye.Application of extension theory in misfire fault diagnosis of gasoline engines[J].Expert Systems with Applocation, 2009, 36(2)∶ 1217−1221.

[20]蔡 文, 杨春燕, 陈文伟, 李兴鑫.可拓集与可拓数据挖掘[M].北京∶ 科学出版社, 2008.CAI Wen, YANG Chun-yan, CHEN Wei-wei, LI Xing-xi.Extension and extension data mining[M].Beijing∶ Science Press,2008.

[21]谢勇谋, 李天斌.爆破对岩爆产生作用的初步探讨[J].中国地质灾害与防治学报, 2004, 15(1)∶ 61−64.XIE Yong-mou, LI Tian-bin.Primary discussion on blast’s affection on rockburst[J].The Chinese Journal of Geological Hazard and Control, 2004, 15(1)∶ 61−64.

[22]朱建军, 刘士新, 王梦光, 黄 敏.供应商选择及订购计划的分析[J].东北大学学报∶ 自然科学版, 2003, 24(10)∶ 956−958.ZHU Jian-jun, LIU Shi-xin, WANG Meng-guang, HUANG Min.Analysis of vendor selection and order planning[J].Journal of Northeastern University∶ Natural Science, 2003, 24(10)∶956−958.

[23]陈加良.基于博弈论的组合赋权评价方法研究[J].福建电脑,2003(9)∶ 15−16.CHEN Jia-liang.Research on evaluation of combined weight based on game theory[J].Fujian Computer, 2003(9)∶ 15−16.

[24]安永林, 彭立敏, 吴 波, 张 峰.隧道坍方突发性事件风险可拓法综合评估[J].中南大学学报∶ 自然科学版, 2011, 42(2)∶514−520.AN Yong-lin, PENG Li-min, WU Bo, ZHANG Feng.Comprehensive extension assessment on tunnel collapse risk[J].Journal of Central South University∶ Science and Technology,2011, 42(2)∶ 514−520.

[25]王元汉, 李卧东, 李启光, 谭国焕.岩爆预测的模糊数学综合评判方法[J].岩石力学与工程学报, 1998, 17(5)∶ 493−501.WANG Yuan-han, LI Wo-dong, LI Qi-guang, TAN Guo-huan.Method of fuzzy comprehensive evaluations for rockburst prediction[J].Chinese Journal of Rock Mechanics and Engineering, 1998, 17(5)∶ 493−501.