合金元素镍对FCC Fe-Cu析出相结构稳定性的影响

温玉锋，孙 坚

(上海交通大学 材料科学与工程学院，上海 200240)

含Cu的铁素体钢或奥氏体钢时效后会析出富Cu第二相，并对铁素体钢或奥氏体钢产生析出强化效应[1−3]。由于热力学平衡相图中Fe-Cu系两组元互溶度很低，并且相互间不形成任何金属间化合物，铁素体钢中的含 Cu析出相在热力学上为亚稳状态。关于铁素体钢中含 Cu析出相的晶体结构一般认为是析出初期为BCC结构，随着析出相中Cu含量的升高转变为9R结构，并最终转变为FCC晶体结构[4]。然而，时效各阶段不同晶体结构析出相中的 Cu含量尚无明确的实验研究结果，同时相关理论研究也还存在很大的争议。GONG等[5]利用分子动力学与第一性原理方法计算了BCC与FCC结构Fe-Cu合金的生成热，计算结果表明，BCC与FCC结构Fe-Cu合金生成热均为正值，说明上述结构Fe-Cu合金在热力学上是不稳定的。当Cu原子的摩尔分数小于40%，Fe-Cu合金为BCC结构时能量较FCC结构能量低；反之，当Cu原子的摩尔分数大于40%，Fe-Cu合金为FCC结构时能量较BCC能量更低。LIU等[6]利用第一性原理研究了BCC Fe-Cu合金的弹性稳定性问题，计算结果表明，BCC Fe-Cu合金的结构稳定性随着Cu含量升高逐渐降低；当Cu原子的摩尔分数不大于50%，BCC结构的Fe-Cu合金满足其晶体结构的Born弹性稳定性准则。本文作者利用特殊准随机结构方法并结合第一性原理计算了不同成分FCC结构的Fe-Cu合金的弹性稳定性问题，计算结果表明，FCC Fe-Cu合金的结构稳定性随着Cu含量升高逐渐升高；当 Cu原子的摩尔分数不小于37.5%时，FCC结构的Fe-Cu合金满足其晶体结构的Born弹性稳定性准则，并可能以亚稳态形式存在[7]。实验研究结果进一步表明，含 Cu的铁素体钢中合金元素Ni的存在有利于铁素体钢中含Cu相的析出，时效后期FCC结构的富Cu析出相中含有较基体更高含量的Ni元素[8−10]。这说明合金元素Ni的存在提高了铁素体钢中FCC结构含Cu析出相的结构稳定性。文献中有关Fe-Cu合金的理论研究主要集中在合金的成分对其结构稳定性的影响，而合金化元素Ni对其结构稳定性影响尚未见报道。因此，本文作者在前期关于FCC结构的Fe-Cu合金的弹性稳定性研究基础上，采用特殊准随机结构(SQS)方法建立Cu原子的摩尔分数分别为25.0%和31.25%两种不同成分FCC结构Fe-Cu无序固溶体晶胞结构，并利用基于密度泛函理论的投影缀加波赝势和广义梯度近似方法，计算研究合金元素Ni对上述两种不同成分FCC结构Fe-Cu无序固溶体包括平衡晶格常数、原子磁矩和生成热等基态性质及其弹性性质，并就合金元素Ni对FCC结构Fe-Cu无序固溶体的结构稳定性进行分析与讨论。

1 计算方法

采用基于密度泛函理论的VASP(Vienna ab initio simulation package)软件包进行理论计算[11]，计算中采用投影缀加波赝势方法(PAW)和广义梯度近似(GGA)形式的 PERDEW(PW91)的势函数来描述交换相关参数[12−14]。平面波的截断能选为425 eV，电子步自洽循环的能量收敛判据为1×10−6eV。在采用特殊准随机结构(SQS)方法建立Cu原子摩尔分数分别为25.0%和31.25% FCC结构Fe-Cu无序固溶体合金晶胞结构的基础上[15]，通过 Ni原子置换(1/2，1/4，1/4)原子坐标上的Fe原子构建两种不同成分的Fe-3.125Ni-25Cu和Fe-3.125Ni-31.25Cu合金，如图1所示。本文所有计算均采用Monkhorst-Pack特殊k网格点方法对布里渊区进行积分[16]，晶胞的k网格点均选取为6×6×6。采用Murnaghan状态方程拟合各晶胞不同体积与能量关系曲线，以得到平衡晶格常数(a0)和体弹性模量(B0)，如式(1)所示：

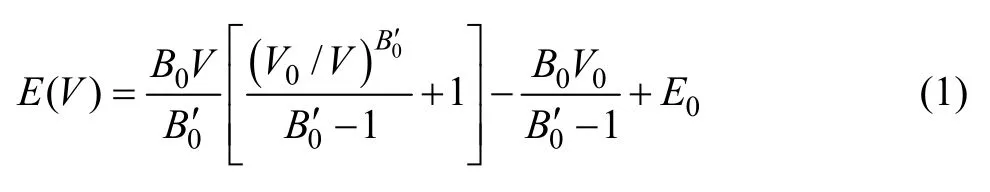
式中：V0为晶胞平衡晶格体积；V为晶胞体积；B0为体弹性模量；0B′为压力系数；E0为平衡体积的能量。

进一步计算合金的生成热和磁矩，其中生成热的计算公式如式(2)所示：

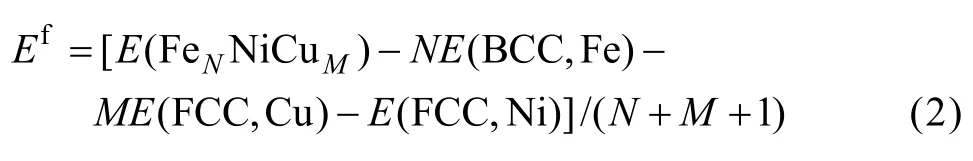
式中：Ef为无序固溶体合金的生成热；N和M分别为合金中Fe和Cu的原子个数；E(FeNNiCuM)、E(BCC,Fe)、E(FCC, Cu)和E(FCC, Ni)分别为无序固溶体的能量、BCC结构Fe、FCC结构Cu和Ni的能量。众所周知，立方结构晶体存在3个独立的弹性常数C11、C12和C44。为了计算FCC结构Fe-Cu和Fe-Ni-Cu合金的弹性常数，可先对晶胞进行不同方式的弹性变形，然后计算出变形后晶胞的能量变化，并通过拟合能量变化与应变关系得到弹性常数。分别给晶胞施加一个等体积的正应变变形和一个等体积的切应变变形，相对应的应变张量ε分别为

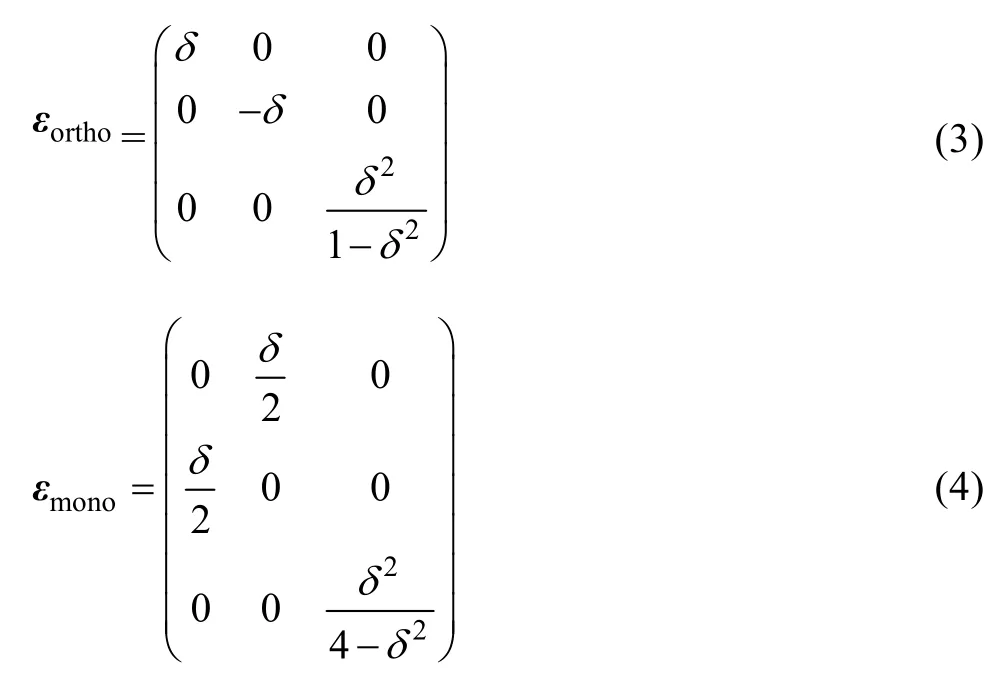
式中：δ为应变，其取值范围为−0.01～0.01，步长为0.002。两种变形引起的能量变化相对应地分别为

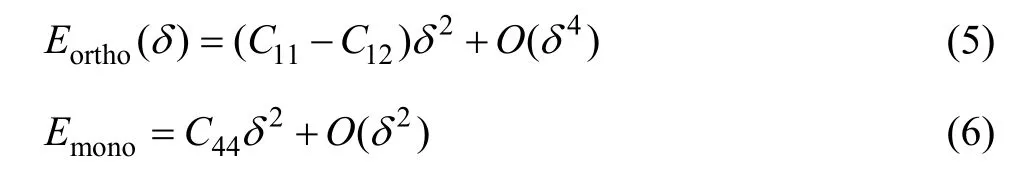
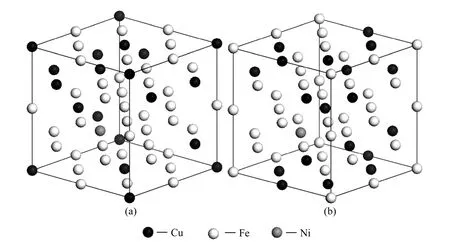
图1 FCC结构Fe-3.125Ni-25Cu和Fe-3.125Ni-31.25Cu无序固溶体合金的特殊准随机结构模型Fig.1 Special quasirandom structure models of FCC structured Fe-3.125Ni-25Cu (a)and Fe-3.125Ni-31.25Cu (b)random alloys

式中：C11、C12和C44为弹性常数；示可忽略高阶无穷小量。

根据式(5)和(6)可直接确定C11−C12和C44。另外，体模量和弹性常数存在以下关系：

因此，联立式(5)和(7)即可计算出C11和C12。

2 计算结果与讨论

首先在无电子自旋极化和电子自旋极化两种条件下对FCC结构Fe-Cu和Fe-Ni-Cu无序固溶体特殊准随机结构晶胞的晶格常数进行优化计算，不同成分Fe-25Cu、Fe-31.25Cu、Fe-3.125Ni-25Cu和Fe-3.125Ni-31.25Cu无序固溶体晶胞能量随晶格常数的变化如图2所示。从能量角度分析FCC结构Fe-Cu和Fe-Ni-Cu无序固溶体存在无磁性和铁磁性两种状态，其中铁磁性状态的能量更趋于稳定。以上不同成分铁磁性Fe-25Cu、Fe-31.25Cu、Fe-3.125Ni-25Cu和Fe-3.125Ni-31.25Cu无序固溶体的平衡晶格常数、生成热、体模量和磁矩的理论计算结果如表1所列。从表1中可以看出：Fe-3.125Ni-25Cu和Fe-3.125Ni-31.25Cu无序固溶体的晶格常数和生成热均比相应 Fe-25Cu和Fe-31.25Cu无序固溶体的小，其中固溶体的生成热仍为正值，这说明 Fe-25Cu、Fe-31.25Cu、Fe-3.125Ni-25Cu和Fe-3.125Ni-31.25Cu无序固溶体在热力学上是不稳定的，但合金元素 Ni的加入使铁磁性的 FCC结构Fe-Ni-Cu无序固溶体的生成热降低。由于晶格常数的减小，所以 Fe-3.125Ni-25Cu和 Fe-3.125Ni-31.25Cu无序固溶体的体模量均比相应Fe-25Cu和Fe-31.25Cu无序固溶体的体模量略有增加。另外，与FCC结构铁磁性Fe-Cu无序固溶体相比较，合金元素Ni的加入使得铁磁性Fe-Ni-Cu无序固溶体的磁矩略有降低。以上不同成分 Fe-25Cu、Fe-31.25Cu、Fe-3.125Ni-25Cu和Fe-3.125Ni-31.25Cu无序固溶体生成热的变化尚不能明确说明其FCC结构稳定性的变化趋势。

根据Born弹性稳定性准则，当立方结构晶体的弹性常数同时满足：时，则立方结构晶体方可存在[17]。因此，正方剪切常数 C′=(C11−C12)/2的大小可以反映立方晶体结构的稳定性变化趋势。铁磁性FCC结构Fe-Cu和Fe-Ni-Cu无序固溶体的弹性常数以及正方剪切模量理论计算结果如表2所列。从表2可以看出，不同成分铁磁性FCC结构 Fe-25Cu、Fe-31.25Cu、Fe-3.125Ni-25Cu和Fe-3.125Ni-31.25Cu无序固溶体合金的弹性常数均为正值，但正方剪切模量 C′不同，其中 Fe-25Cu和Fe-3.125Ni-25Cu两种合金的正方剪切模量小于0，而Fe-31.25Cu和Fe-3.125Ni-31.25Cu两种合金的正方剪切模量却大于0。可见，铁磁性FCC结构Fe-25Cu和Fe-3.125Ni-25Cu无序固溶体不满足Born弹性稳定性准则，而Fe-31.25Cu和Fe-3.125Ni-31.25Cu无序固溶体满足Born弹性稳定性准则，可以亚稳态形式存在。随着 Cu含量的增加，铁磁性 FCC结构 Fe-Cu和Fe-Ni-Cu固溶体的正方剪切模量C′均从负值向正值变化，说明 Cu含量的增加可以提高铁磁性 FCC结构Fe-Cu和Fe-Ni-Cu无序固溶体的结构稳定性。从表2也可以看出，Fe-3.125Ni-31.25Cu无序固溶体的正方剪切模量C′明显地较Fe-31.25Cu的大，说明合金元素Ni的加入可以提高亚稳态铁磁性FCC结构Fe-Cu无序固溶体的结构稳定性。

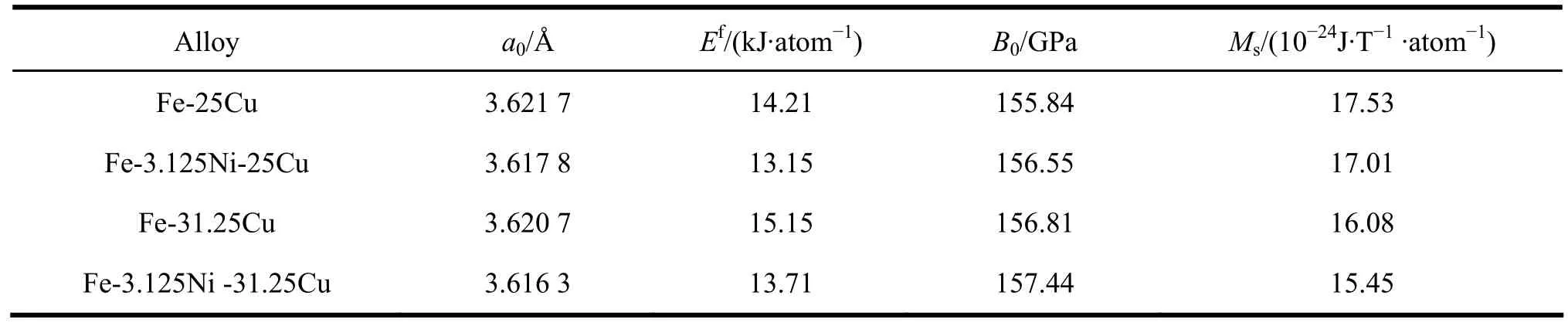
表1 FCC结构Fe-Cu和Fe-Ni-Cu无序固溶体的平衡晶格常数(a0)、生成热(Ef)、体模量(B0)和磁矩(Ms)Table 1 Lattice constant (a0), heat of formation (Ef), bulk modulus (B0)and magnetic moment (Ms)of FCC structured Fe-Cu and Fe-Ni-Cu random solid solutions

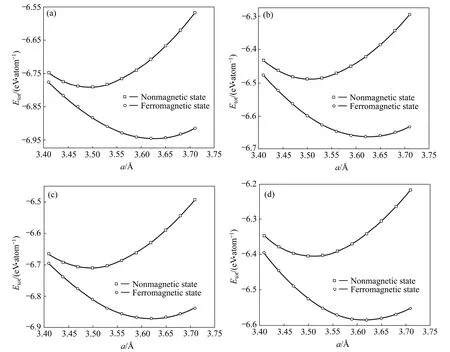
图2 FCC结构Fe-Cu和Fe-Ni-Cu无序固溶体总能量(Etot)随晶格常数(a)的变化关系Fig.2 Relationship between total energy (Etot)and lattice constant (a)of FCC structured Fe-Cu and Fe-Ni-Cu random solid solutions∶ (a)Fe-25Cu; (b)Fe-31.25Cu; (c)Fe-3.125Ni-25Cu; (d)Fe-3.125Ni-31.25Cu

进一步计算不同成分铁磁性 FCC结构Fe-31.25Cu、Fe-3.125Ni-25Cu和 Fe-3.125Ni-31.25Cu无序固溶体的电子态密度分布，计算结果分别如图3和 4所示。从图3中可以看出：铁磁性 FCC结构Fe-31.25Cu和Fe-3.125Ni-31.25Cu无序固溶体的态密度分布曲线的峰形十分相似，合金元素Ni的加入使其态密度分布向低能区域移动，从而导致费米能以下的成键态密度增加；同时合金元素Ni的加入使其费米能级处的态密度值减小，说明Fe-3.125Ni-31.25Cu固溶体也越趋于稳定。图4同时表明固溶体中Cu含量的增加也使 Fe-Ni-Cu无序固溶体态密度分布向低能区域移动，从而导致费米能以下的成键态密度增加；并使其费米能级处的态密度值降低，FCC结构Fe-Ni-Cu无序固溶体也越趋于稳定。这与以上弹性性质计算结果一致。曹悦等[8]利用计算机模拟与透射电子显微镜观察分析了添加合金元素Ni前后铁素体钢中含Cu析出相的析出动力学与含 Cu析出相形貌及成分，结果表明，合金元素Ni的加入可降低含Cu析出相的形核能量，促进含 Cu析出相沉淀析出和长大粗化。周邦新等[9−10]采用原子探针层析技术和时效模拟方法研究了反应堆压力容器模拟钢中富 Cu原子团簇的析出及Ni含量对富Cu原子团簇析出的影响，结果表明，提高钢中Ni含量会促使富Cu原子团簇的析出，而且时效后期富Cu析出相中Ni元素的含量较基体的更高。

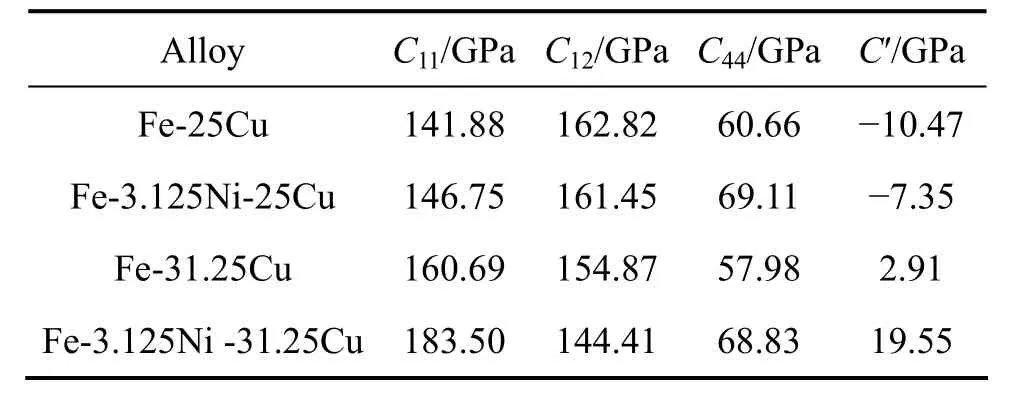
表2 铁磁性FCC结构Fe-Cu以及Fe-Ni-Cu无序固溶体的弹性常数Table 2 Elastic constants of ferromagnetic FCC Fe-Cu and Fe-Ni-Cu random solid solutions

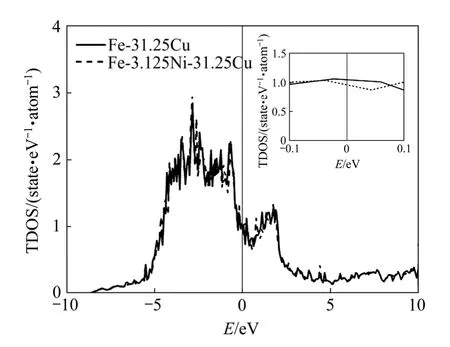
图3 铁磁性FCC结构Fe-31.25Cu和Fe-3.125Ni-31.25Cu无序固溶体总电子总态密度(TDOS)分布Fig.3 Total density of states (TDOS)of ferromagnetic FCC structured Fe-31.25Cu and Fe-3.125Ni-31.25Cu random solid solutions

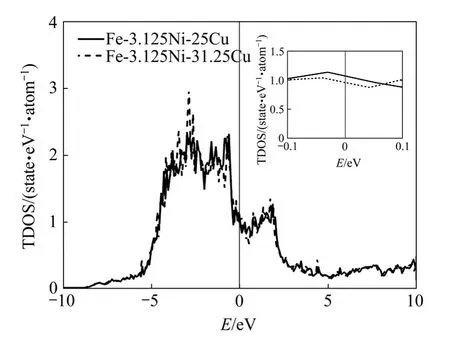
图4 铁磁性 FCC结构 Fe-3.125Ni-25Cu和 Fe-3.125Ni-31.25Cu无序固溶体电子总态密度(TDOS)分布Fig.4 Total density of states (TDOS)of ferromagnetic FCC structured Fe-3.125Ni-25Cu and Fe-3.125Ni-31.25Cu random solid solutions

本文作者关于正方剪切模量以及电子结构的理论计算结果表明，Fe-Ni-Cu无序固溶体中Cu含量的增加以及合金元素Ni的加入使得铁磁性FCC结构Fe-Ni-Cu无序固溶体的结构稳定性显著增加，这就从理论上解释了含Cu的铁素体钢中合金元素Ni的存在有利于铁素体钢中含Cu相的析出，以及时效后期FCC结构的富Cu析出相中含有较基体更高含量的Ni元素等实验事实。

3 结论

1)能量分析表明FCC 结构Fe-Cu和Fe-Ni-Cu无序固溶体存在无磁性与铁磁性两种状态，其中铁磁性Fe-Cu和Fe-Ni-Cu无序固溶体能量相对较低。

2)铁磁性FCC结构Fe-25Cu和Fe-3.125Ni-25Cu无序固溶体不满足 Born弹性稳定性准则，而Fe-31.25Cu和 Fe-3.125Ni-31.25Cu无序固溶体满足Born弹性稳定性准则，可以亚稳态形式存在。

3)Cu含量的增加可以提高铁磁性 FCC结构Fe-Cu和Fe-Ni-Cu无序固溶体的结构稳定性，合金元素Ni的加入使得亚稳态铁磁性FCC结构Fe-31.25Cu无序固溶体的结构稳定性进一步显著增加。

[1]ZHANG Z W, LIU C T, WANG X L, MILLER M K, MA D,CHEN G, WILLIAMS J R, CHIN B A.Effects of proton irradiation on nanocluster precipitation in ferritic steel containing fcc alloying additions[J].Acta Materialia, 2012, 60(6/7)∶3034−3046.

[2]REN L, ZHU J M, NAN L, YANG K.Differential scanning calorimetry analysis on Cu precipitation in a high Cu austenitic stainless steel[J].Materials and Design, 2011, 32(7)∶ 3980−3985.

[3]CHI C Y, YU H G, DONG J X, XIE X S, CUI Z Q, CHEN X F,LIN F S.Strengthening effect of Cu-rich phase precipitation in 18Cr9Ni3CuNbN austenitic heat-resisting steel[J].Acta Metallurgica Sinica∶ English Letters, 2011, 24(2)∶ 141−147.

[4]KOBAYASHI S, TAKEDA T, NAKAI K, HAMADA J I,KANNO N, SAKAMOTO T.Effect of Nb addition on Cu precipitation in ferritic stainless steel[J].ISIJ International, 2011,51(4)∶ 657−662.

[5]GONG H R, KONG L T, LIU B X.Structural stability and magnetic properties of metastable Fe-Cu alloys studied by ab initio calculations and molecular dynamics simulations[J].Physical Review B, 2004, 69(5)∶ 054203−054210.

[6]LIU J Z, van de WALLE A, GHOSH G, ASTA M.Structural,energetic, and mechanical stability of Fe-Cu bcc alloys from first-principles calculations[J].Physical Review B, 2005, 72(14)∶144109−144123.

[7]温玉锋, 孙 坚, 黄 健.基于特殊准随机结构模型的 FCC Fe-Cu无序固溶体合金的弹性稳定性[J].中国有色金属学报,2012, 22(9)∶ 2522−2528.WEN Yu-feng, SUN Jian, HUANG Jian.Elastic stability of face-centered cubic Fe-Cu random alloys based on special quasirandom structure[J].The Chinese Journal of Nonferrous Metals, 2012, 22(9)∶ 2522−2528.

[8]曹 悦, 张 弛, 杨志刚, 夏志新.镍对Fe-Cu-Ni合金中铜析出行为的影响[J].钢铁研究学报, 2012, 24(1)∶ 54−58.CAO Yue, ZHANG Chi, YANG Zhi-gang, XIA Zhi-xin.Influence of Ni on Cu precipitation in Fe-Cu-Ni alloy[J].Journal of Iron and Steel Research, 2012, 24(1)∶ 54−58.

[9]周邦新, 王均安, 刘庆东, 刘文庆, 王 伟, 林民东, 徐 刚,楚大锋.Ni对RPV模拟钢中富Cu原子团簇析出的影响[J].中国材料进展, 2011, 30(5)∶ 1−6.ZHOU Bang-xin, WANG Jun-an, LIU Qing-dong, LIU Wen-qing, WANG Wei, LIN Min-dong, XU Gang, CHU Da-feng.Effect of nickel alloying element on the precipitation of Cu-rich clusters in RPV model steel[J].Materials China, 2011, 30(5)∶1−6.

[10]朱娟娟, 王 伟, 林民东, 刘文庆, 王均安, 周邦新.用三维原子探针研究压力容器模拟钢中富铜原子团簇的析出[J].上海大学学报∶ 自然科学版, 2008, 14(5)∶ 525−530.ZHU Juan-juan, WANG Wei, LIN Min-dong, LIU Wen-qing,WANG Jun-an, ZHOU Bang-xin.3D atomic probe characterization of precipitation of Cu-rich clusters in pressure vessel model steel[J].Journal of Shanghai University∶ Natural Science, 2008, 14(5)∶ 525−530.

[11]KRESSE G, FURTHMŰLLER J.Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set[J].Physical Review B, 1996, 54(16)∶ 11169−11186.

[12]KRESSE G, JOUBERT D.From ultrasoft pseudopotentials to the projector augmented-wave method[J].Physical Review B, 1999,59(3)∶ 1758−1775.

[13]BLŐCHL P E.Projector augmented-wave method[J].Physical Review B, 1994, 50(24)∶ 17953−17979.

[14]PERDEW J P, CHEVARY J A, VOSKO S H, JACKSON K A,PEDERSON M R, SINGH D J, FIOLHAIS C.Atoms, molecules,solids, and surfaces∶ Application of the generalized gradient approximation for exchange and correlation[J].Physical Review B, 1992, 46(11)∶ 6671−6687.

[15]von PEZOLD J, DICK A, FRIÁK M, NEUGEBAUER J.Generation and performance of special quasirandom structures for studying the elastic properties of random alloys∶ Application to Al-Ti[J].Physical Review B, 2010, 81(9)∶ 094203−094209.

[16]MONKHORST H J, PACK J D.Special points for Brillouinzone integrations[J].Physical Review B, 1976, 13(12)∶5188−5192.

[17]BORN M, HUANG K.Dynamical theory of crystal lattices[M].Oxford∶ Clarendon Press, 1954∶ 141.