Review of snow grain size retrieval from remote sensing

ZhongMing Guo ,HongBo Wu,RuiJuan Mao,ChunWen Zhang,YuWei Wu

State Key Laboratory of Cryospheric Science,Cold and Arid Regions Environmental and Engineering Research Institute,Chinese Academy of Sciences,Lanzhou,Gansu 730000,China

1 Introduction

Grain size is a fundamental parameter characterizing snow/firn properties (Domineet al.,2008).Spatial and temporal changes in snow grain size can help us characterize the thermal state of the snowpack,and to estimate the timing and spatial distribution of snowmelt (Nolin and Dozier,1993).Spatial and temporal changes in snow grain size are also input parameters of snowmelt runoff,snow chemical and climate models.Snow particle size changes are conducive to the identification of ice sheet surface characteristics,for example,ablation area,dunes and pure ice area,and can indicate the energy balance of snow/firn (Nolin and Stroeve,1997).Snow grain size is the main parameter influencing broadband albedo,so it also plays a key role in the Earth radiation balance (Caoet al.,2006).Space-borne remote sensing of the Earth in the visible (about 0.4-0.7 μm),near infrared (NIR,about 0.7-1.4 μm) and shortwave infra-red (SWIR,about 1.4-2.5 μm) regions has been used to estimate grain size at large spatial scales and moderate-to-high spatial resolution.

Wiscombe and Warren (1980) indicated the decrease of spectral reflectance combined with the increase of snow grain size.Dozieret al.(1987) used the Wiscombe-Warren model and NOAA-6 AVHRR data and concluded that it was"potentially possible" to determine snow grain size from remote sensing data.However,their results were imprecise because the width and position of NOAA-6 AVHRR near-infrared band limit its sensitive to snow grain size.With the development of remote sensing technology,Landsat TM/ETM+,MODIS,AVIRIS and Hyperion data were used for snow grain size retrieval.Dozier and Marks (1987) used Landsat TM data to classify snow-covered regions into relatively fine-grain new snow and older snow,and coarser-grained snow,but no synchronous ground measurements were made for confirmation.Hyvärinen and Lammasniemi(1987) measured the near-infrared reflectance of snow grains in three size classes and related changes in a reflectance ratio of bands centered at 1.03 μm and 1.26 μm to changes in average grain diameter.Nolin and Dozier (1993) used a retrieve technique and collected data by AVIRIS,and estimated the snow grain size for the near-surface snow layer to calculate the Tioga Pass region and Mammoth Mountain in Sierra Nevada,California.Afterwards,they employed a radiative transfer model,which relates an ice absorption feature,centered at λ=1.03 μm,to the optically equivalent snow grain size (Nolin and Dozier,2000).Jinet al.(2008) investigated the single scattering optical properties of snow for different ice particle shapes and degrees of microscopic scale roughness and noted that snow optical properties with an aggregate assumption were applied to the retrieval of snow grain size over the Antarctic Plateau by analyzing numerous particle shapes.Jianget al.(2009) used the spectrum reflection curves of different grain size of snow measured in Binggou Basin,and analyzed the spectral reflection characteristics of snow.Lyapustinet al.(2009) retrieved snow grain size over Greenland by MODIS data.Liang and Wang (2009) obtained the snow reflectance image through the Hyperion image,and the retrieval snow reflectance image might become the base image for further work,such as extracting area of snow cover,snow grain size,and snow surface albedo.

While non-domestic research on snow grain size remote sensing inversion has made great progress,domestic research is only at the beginning stage.Development of satellite remote sensing of snow is of great importance,particularly for monitoring of snow age,pollution and grain sizes over difficult-to-access polar regions (Zegeet al.,2008).We can obtain detailed observations of snow grain size change in local regions by field measurements,but remote sensing data and interpretation results can help us obtain temporal and spatial change features of snow grain size.

2 Basis of snow grain size retrieval from remote sensing

2.1 Related conception of various snow grain sizes

From the point of view of remote sensing,snow grain size is generally divided into optical and physical grain size.Optical grain size is a function of the distance between scattering opportunities (i.e.,air bubbles or internal grain boundaries),including optical equivalent grain size and optical effective grain size.Dobbins and Jizmagian (1966)demonstrated that the volume-to-surface area ratio of ice particles was an appropriate means for representing optically equivalent grain size.NIR band and visible band albedo ratio can be used to calculate optical effective grain size.Physical grain size is the actual snow grain size.In general,optical snow grain size does not equal physical grain size,caused by grain size field measurement technology,instrument radiation calibration,no Lambert scattering,solar irradiance and atmospheric correction.Thus,the translation from optical to physical grain size may be a function of snowpack conditions.

Additionally,there are other methods for obtaining snow grain size,such as mean convex radius.The mean convex radius may simply be computed as the mean radius of the curves locally fitting the discrete convex contour (Lesaffreet al.,1998).The accuracy of this method depends on the number (N) of contour pixels used to fit the discrete contour.

2.2 Snow grain shape

Because of the complexity of particle shape,accurate calculation of the single scattering properties of a snow grain is a challenge.Snow grains are usually nonspherical and tend to be spheroidal and randomly oriented.Scattering models for spherical particles are much simpler than for other shapes,so we generally assume that an "equivalent sphere" can simulate the behavioral properties of nonspherical shapes.Mugnai and Wiscombe (1987) demonstrated that a collection of unoriented nonspheroids produce the same scattering results as spheres.The conventional way to establish the relation between radiative and retrieved microphysical characteristics is to use the Mie theory to obtain single-scattering characteristics,which is a relationship between radiative properties of snow layers and single-scattering (inherent)characteristics based on the radiative transfer theory.The usual "equivalent spheres" assumption significantly overestimates forward reflected radiance,and underestimates backscattering radiance,around the principal plane.A potentially more realistic assumption of non-spherical close-packed grains notes that snow grain shape is not determined a priori;moreover,various snow grain shapes depend on the origin and age of snow and the environment.Such a model was suggested by Zegeet al.(2008).

2.3 Snow grain size retrieval principle

The snow grain size retrieval principle based on the proposition of Wiscombe and Warren (1980) states that there is weak absorption by pure ice in the visible band,but strong absorption in the NIR/SWIR band.The spectral reflectance of snow varies significantly with wavelength (Figure 1).In the visible part of the spectrum (0.4-0.7 μm),ice is weakly absorbing and strongly forward-scattering,and snow has a high reflectance.Strong absorption causes snow reflectance to obviously decline in the middle-infrared band part of the spectrum (0.7-3.0 μm) where snow reflectance is sensitive to snow grain size,thus the retrieval method depends on moderate absorption of ice in the near-infrared band (0.7-3.0 μm),particularly in the 0.7-1.4 μm spectral region.In general,the radiative transfer model is used to relate the optical properties of snowpacks to physical properties such as snow grain size.The models include the discrete-ordinate model and two-stream radiative model,the former is able to calculate the angular distribution of reflected radiation,and the latter can calculate the hemispherical integrated reflectance.

3 Model and algorithm

Over the past 30 years,researchers have provided numerous reversion models.With the development of remote sensing technology,numerous rapid practical algorithms and technologies have been exploited.

3.1 Wiscombe-Warren model

The Wiscombe-Warren (WW) model (Wiscombe and Warren,1980) can accurately reflect snow spectral reflectance,describe snow grain size,solar zenith angle,snowpack thickness and the ratio of diffuse to direct solar incidence influence on the spectral albedo.This model does neglect the nonsphericity of snow grains and near-field scattering,and uses the delta-Eddington approximation for multiple scattering together with the Mie theory for single scattering.This model also relates the optical properties of snowpack to physical properties such as correlating snow grain size to reflectivity in order to estimate snow grain size.Another important feature of the WW model is its input parameters which are collected by measurements,and which are widely available and relatively easy to operate.

Figure 1 The spectral directional hemispherical reflectance of snow as calculated using the DISORT model (Stamnes et al.,1988)

3.2 Nolin-Dozier model

Nolin and Dozier (1993) developed the snow grain size inversion algorithm by the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS).The wavelength of 1.04 μm was chosen because it is in a spectral region where reflectance is particularly sensitive to grain radius size.There is an additional advantage in using a band centered at that wavelength,namely little atmospheric scattering or attenuation in this region influencing radiation propagation.For each image,curve of reflectance vs.snow grain size is fit with an exponential model ofR=arbwhereRis the calculated grain radius,ris the single band reflectance anda,bare coefficients using a method of least-squares fitting.As the relationship between snow grain size and reflectance is also controlled by solar altitude (especially when solar altitude is greater than 30°),it is necessary to know the angle of solar incidence before proceeding with the calculation (Figure 2).

In order to obtain surface reflectance in an image from satellite and high-altitude image data,we must correct the effects of the atmosphere.One should note that these optically equivalent grain radii do not represent depth-averaged grain size for the entire snowpack.Rather,they are strongly weighted by the snowpack surface layer grain size.

3.3 Single channel retrieval algorithm

Snow grain size can also be obtained from satellite single channel data or band ratio method.It is necessary to obtain the directional reflectance factorR0.Nolin and Dozier (1993)quantitatively estimated snow grain size by the single AVIRIS band data centered at 1.03 μm because (1) at this wavelength snow reflectance is highly sensitive to grain size;(2) there is still a strong snow reflectance signal;and (3) atmospheric transmittance is high.There are two drawbacks of this method,one is the effect of sensor noise when the interpretation is based on the signal in one wavelength band,and the other is the requirement for knowledge of the angle between sun and sensor.Lyapustinet al.(2009) retrieved snow grain size over Greenland from single MODIS band,and proposed that there is a difference between MODIS reflectance and theory predicted value,mainly as the local topographic change causing the change of macro surface roughness.

3.4 Band-ratio retrieval algorithm

Hyvärinen and Lammasniemi (1987) related changes in a reflectance ratio of near-infrared bands,centered at 1.03 μm and 1.26 μm,to changes in average ice grain diameter for three size classes of ice particles from a series of laboratory experiments.Kayet al.(2003) used multispectral MODIS/ASTER Airborne Simulator (MASTER) data,and estimated optical grain size and physical grain size by MASTER-derived spectra near 1.8 μm and 2.2 μm.Scambos and Haran (2007) used a normalized difference index derived from MODIS band 1 and band 2 radiance values to determine optical grain size.Estimation from directional reflectance variation to snow grain size were accomplished by a look-up table,generated by a combination of published models of snow spectral reflectance and atmosphere radiative transfer.Band ratio method reduces the effect of shadow and subpixel shelter by surface roughness.

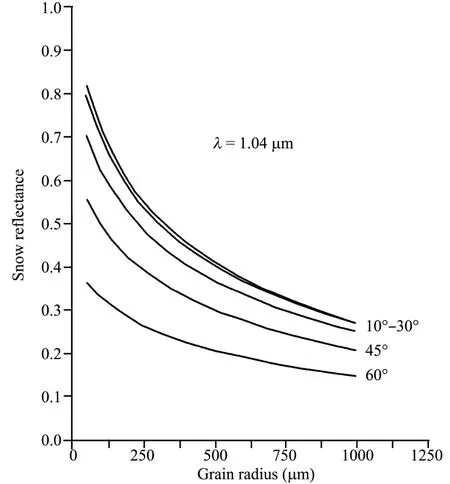
Figure 2 Snow reflectance modeled as a function of equivalent grain size for solar incident beam angles(Nolin and Dozier,1993)

3.5 Scaled-band method

Clark and Roush (1984) recognized that an "apparent continuum" could represent the characteristic absorption spectrum in which it is interested.They calculated the scaled band depthDbthrough continuous reflectanceRcand reflectance spectrumRbin the strongest absorption band,that is:

The advantage of scaling the band depth by continuous reflectance is that the estimation of grain size becomes independent of the absolute magnitude of reflected radiance,thereby this method is not sensitive to topography.Although this band-depth method is a valuable approach to the problem,the accuracy of the results is influenced by noise in the reflectance spectrum as this method only depends on a single spectral band.Noise-induced changes in the spectrum affect the depth of the absorption feature and may give erroneous grain size estimation.

To minimize any effects of noise on grain size retrieval,Nolin and Dozier (2000) scaled area of the absorption feature,Ab,rather than simply scaled absorption band depth.Abis a dimensionless quantity and is calculated by integrating the scaled absorption band depth over the wavelengths of the absorption feature,shown in Equation(2):

The Equation(2)basic assumption is that noise is randomly distributed as Gaussian noise ("white noise").While the exact distribution of sensor noise is unknown,the normal distribution assumption is reasonable (Sabolet al.,1992).By integrating over the characteristic absorption band,the fluctuations caused by noise should average out and produce an estimate closer to the true value.Then Clark and Roush(1984) used the DISORT model to calculate spectral reflectance for the same 17 AVIRIS channels.For each grain size,we calculate a scaled band area from the model-derived spectral reflectance,and we create a lookup table in which the scaled band areas are juxtaposed with their corresponding snow grain radii.Figure 3 shows the relationship between scaled band area and grain size.

Figure 3 The nonlinear relationship between snow grain radius and scaled band area (Nolin and Dozier,2000)

Jianget al.(2009) analyzed detailed spectral features such as the differences of spectral reflection values near 1,030 nm and 1,250 nm bands,absorption band depth and area near 1,030 nm band,and fitted them to snow grain size.By comparison,it is revealed that absorption band area has a best fit linear and exponential relationship with grain size.This is attributed to the spectral absorption area that represents the surface features relative reflectance,which can not only reduce the error caused by terrain and clouds,but also averages spectrometer noise caused by itself,so as to achieve a better fitting effect.Limitations of the method are as follows:(1) the pixel must be completely snow-covered;(2) dirty snow conditions will reduce the absorption feature,thereby reduce the retrieved grain size;(3) the method requires sufficient spectral resolution to measure the reflectance.

3.6 SGSP algorithm

Zegeet al.(2008) presented an algorithm to retrieve the effective snow grain size and soot concentration from snow spectral reflectance data measured by an optical instrument on a satellite.The algorithm is based on the fact that the snow layer is composed of closely-packed medium of irregularly shaped grains,then inversing snow grain size as the snow albedo is the function of snow grain size.From the asymptotic theory it can be concluded that:

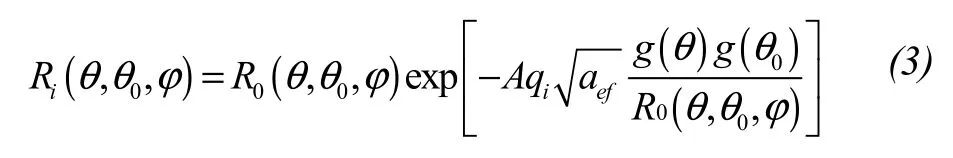
where,Ri(θ,θ0,φ) is radiance coefficient of radiation reflected;θandθ0are polar (zenith) angles of the observation and the sun,respectively;φis the azimuth angle.R0(θ,θ0,φ)is the radiance coefficient of the semi-infinite non-absorbing layer;g(θ) is universal function;aefis the effective size of grains,as this technology calculated the snow reflectance with soot,so it includes the soot qualityqi.

SGSP (snow grain size and pollution) algorithm uses data in three channels to retrieve effective snow grain size and soot concentration,and use the extra channel to eliminate direct dependence of functionR0(θ,θ0,φ) on prior unknown phase function (i.e.,particle shapes).The effective snow grain sizeaefis retrieved using data in visible and near-IR spectrum channels.The spectral channels should be chosen without the spectrum of ice absorption.As shapes of snow grains in one pixel are unknown,adopting any prior model may lead to non-controlled retrieval errors.The main advantage of the proposed algorithm over any current use is the independence of any prior snow particle model.The SGSP analytical retrieval provides extremely fast satellite data processing.The algorithm can be generalized for other satellite instruments with appropriate spectral channels.

3.7 AART snow reflectance model

Kokhanovsky and Zege (2004) developed the Analytical Asymptotic Radiative Transfer (AART) model of snow reflectance.The snow grains are modeled as fractal rather than spherical particles in order to account for their irregular shape.The retrieval is theoretically based on an analytical asymptotic radiative transfer model which predicts spectral bidirectional snow reflectance as a function of grain size and ice absorption.This model predicts snow reflectance using an asymptotic analytical solution of the radiative transfer problem in semi-infinite media with low absorption (namely Milne problem),which is reliable at estimating snow characteristics in visible spectral range:

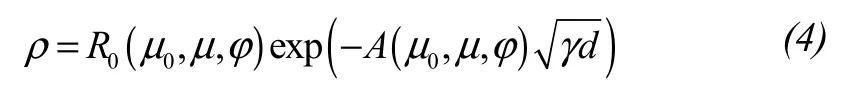
here,γ=4πχ/λ,χis imaginary part of refractive index of ice,λis wavelength,andd=6〈V〉/〈S〉 is an effective grain size defined by ratio of the average volume to the average surface area of grains.R0is a solution of radiative transfer equation for snow with zero absorption.Lyapustinet al.(2009) developed the rapid algorithm which used the analytic asymptotic solution form and MODIS reflectance ratio of band 5(1.24 μm) and band 1 (0.645 μm).Liet al.(2001) pointed out additional retrievals in SWIR bands 6 (1.6 μm) and 7(2.11 μm) where higher snow absorption and lower light penetration depth can potentially be used to evaluate vertical profile of grain size.

3.8 MODSCAG model

Painteret al.(2009) built the MODIS Snow-covered Area and Grain Size (MODSCAG) model in a subpixel scale to obtain the snow reflectance.In contrast to models relying on absolute reflectance,the MODSCAG model uses the relative shape of the snow’s spectrum and can be applied to mountainous areas where local solar illumination angle on a slope is often unknown because of co-registration errors between the image and a digital elevation model.The MODSCAG model estimates the fraction of each pixel that is covered by snow,along with snow grain size.

MODSCAG incorporates the following assumptions:(1)the variability of the hemispherical-directional reflectance factor for solar geometry and atmospheric conditions at the time when each MODIS is acquired is negligible;(2) the effects of impurities and thin snow on snow spectral reflectance are separable and these effects do not impact retrieval of snow area and grain size;(3) linear spectral mixture analysis is valid for multispectral scenes of alpine terrain;and (4)liquid water in the snow does not affect the retrieval of snow-covered area and grain size.

4 Result and validation

At present,snow grain size inversion research has been carried out in many regions.Lyapustinet al.(2009) estimated snow grain size over Greenland,and compared with the grain size collected by the lens (Aokiet al.,2007),then found that retrieved optical diameter from AART model may need a correction factor.The retrieval correlates well with measurements of radii in the range of about 0.1-1 mm.The derived grain size from MODIS over selected sites in 2004 was compared to the microwave brightness temperature measurements of SSM/I radiometer which is sensitive to the amount of liquid water in the snowpack.The comparison shows a good qualitative agreement,with both datasets detecting two main periods of snowmelt,as cloud cover does not impact SSM/I data.Additionally,MODIS grain size was compared with predictions of the snow model CROCUS driven by automatic weather stations of the Greenland Climate Network (CROCUS;Brunet al.,1989).Some of the deviation between MODIS and CROCUS might be caused by cloudiness.Because of inevitable errors in cloud detection,when cloudy pixels are masked as clear,the developed algorithm may produce lower grain size values in cloudy conditions.Overall,the agreement between CROCUS and MODIS results was satisfactory,particularly before and during the first melting period in mid-June.Detailed time series analysis of snow grain size in 2004 demonstrated a consistency of the time series of retrieved grain size and a good sensitivity of the algorithm to detect snowmelt and at least a few snow precipitation events.

Painteret al.(2007) stated that the effective grain radius is overestimated because observers tend to focus on larger grains,therefore Painteret al.(2009) validated grain size retrieval with measurements in 2002 and 2003 during the Cold Land Processes Experiment (CLPE).Field teams were trained to estimate representative grain sizes instead of the largest grains.The mean absolute error across the data was 51 μm and the mean error was 30 μm,indicating that MODSCAG retrieves a larger grain size than that from field measurements.Additionally,errors increased with increasing grain size.This result is consistent with the non-linear relationship between reflectance and grain size.

Filyet al.(1997) compared simultaneous remote sensing and ground truth data in April and December of 1992 in the French Alps,and discovered that optical grain size is close to the measured one in the near-Infrared channel TM4,but Landsat-derived snow reflectance is not accurate enough to allow a reflection of grain size.For the middle infrared channels TM5 and TM7,the computed optical snow grain size is very different from the measured one,but a linear relationship was found between those data under very different solar irradiance conditions in April and December.Using ratios between channels instead of a single channel can give qualitative estimates of grain size.

Nolin and Dozier (2000) calculated the snow grain size using AVIRIS data over the Mammoth Mountain through the scaled band area method.Figure 4 shows that grain sizes are the smallest at the highest elevations and somewhat larger at lower elevations.The elevation differences in grain size most likely reflect different rates of metamorphism caused by temperature differences.Further tests using ground-based field spectrometer data and measuring grain sizes indicate that the scaled band area method is valid over the range of possible grain sizes.

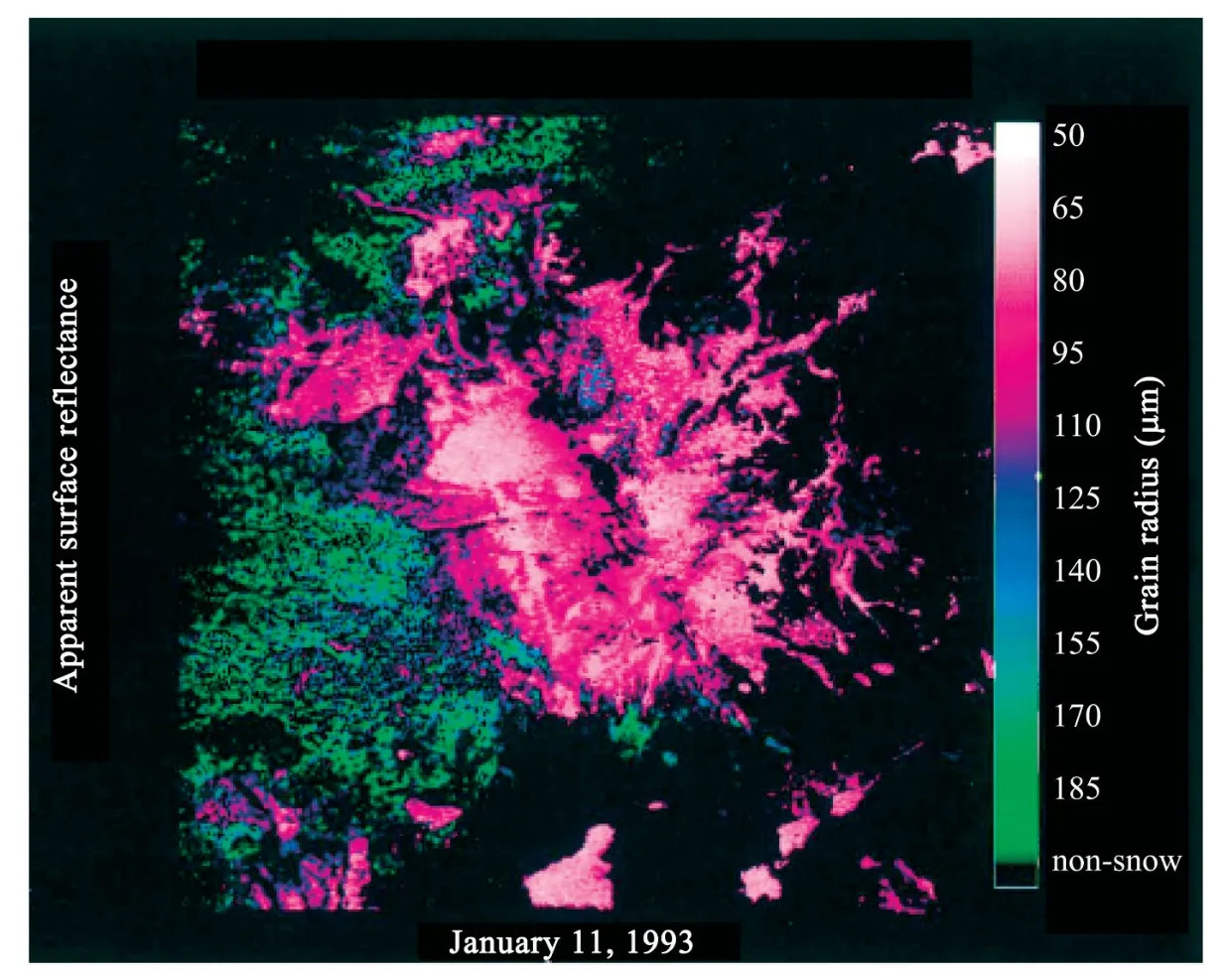
Figure 4 Grain size image of Mammoth Mountain,Calif.(Nolin and Dozier,2000)

Moreover,we can measure snow grain size by stereology technology to validate the retrieval grain size.The advantage of stereology technology is the high precision analyses,but the disadvantage is time-consuming,such as dealing with snow samples,stereology analysis and calculations.In addition,we can use other representative bands which are sensitive to grain size and combined with other sensors with the same sensor (i.e.,CERES,clouds and the Earth radiation system) to test the inversion results.

In the validation process,we can realize validation of remote sensing surface data mainly through the fixed point of continuous time series observation or snow layer at different altitude multipoint observations.

5 Discussion

Many parameters influence snow grain size retrieval,such as temperature,liquid water content and contaminant.Temperature greatly affects snow grain size inversion,and grain growth is exponentially proportional to snow temperature (Jordan,1991).In the spectral region around 1 μm,both liquid water and ice have different absorption features.Ideally,for grain size mapping method,it would be best if there were no overlap between liquid water and ice absorption features.However,some small amount of overlap under very wet snow conditions could have a small effect on the 1.03-μm absorption feature.Green and Dozier (1996)demonstrated that in the presence of liquid water,ice absorption feature shifts to shorter wavelengths and becomes less deep.Warren and Wiscombe (1980) stated that light-absorbing particulates,such as soot and dust,present in minute quantities in most snowpack,and when acquiring sufficient amounts,cause a substantial decrease in the visible reflectance of snow.Bourdelles and Fily (1993) noted that the retrieved size depends on the radiation-penetration depth,which is wavelength-dependent.The wavelength dependence of the radiation penetration depth implies that the retrieved snow grain size will depend on the channel or band used by reflection process.The penetration depth increases with increasing snow grain size for a fixed wavelength,the longer the wavelength,the smaller retrieved snow grain size(Stamneset al.,2007).Additionally,at high solar zenith angle,some grain size measurements were affected by both off-nadir viewing and the lack of a relative azimuth correction,leading to low or even negative optical grain size values.

Furthermore,snow grain size inversion may be caused by factors such as precipitation,snow depth,sensor noise,deformation,aeolian deposit,tiny terrain changes and small amount of clouds.

6 Prospect

In general,snow grain size retrieval began with atmosphere correction for remote sensing data,based on the fact that there is weak absorption of pure ice in the visible band and strong absorption in the NIR/SWIR band,and snow reflectance is sensitive to snow grain size,then a radiative transfer model is used to relate optical properties of snowpack to physical properties such as snow grain size.Although visible,near infrared,short wave infrared and thermal infrared images can be used to quantitatively estimate snow properties,limitations still exist in terms of technology and system.Different conception of snow grain size,grain shape,penetration depth,wavelength,view geometry,temperature and impurity content in the snow will affect the snow grain size inversion.Reflectance estimation and instrument noise can reduce accuracy of the snow properties inversion.Tiny terrain changes and a small amount of clouds can also cause snow reflectance change,and introduce error to snow grain size and reflectance fitting.

The key to snow grain size inversion is choosing the sensor and the inversion model or algorithm.Imaging spectrometers such as AVIRIS and Hyperion possess the appropriate band locations for sensitivity to snow grain size and the narrow bandwidths for high precision.A series of models and algorithms have their own advantages and disadvantages,such as band ratio method weakens the effects of shadows and sub-pixel shadowing due to surface roughness.Scaled-band area technology is a better indicator for snow grain size and fits well with the linear and exponential curve of the grain size.

In addition,the current inversion method is basically used in polar regions and flat areas because of the relatively simple topography,dry and clean snow,less aerosol and water vapor content in these regions.Consequently,in steep mountain terrain,we should improve the inversion method or develop a new algorithm.For example,we can correct the remote sensing image by using DEM data,as well as enhance the ability to filter clouds and distinguish between snow and cloud.

Funding for this research was provided by National Science Fundamental Key Project (40930526,40901041),and Science Research Program of Global Change Research of China (Grant No.2010CB951404).

Aoki T,Hori M,Motoyoshi H,Tanikawa T,Hachikubo A,Sugiura K,Yasunari TJ,Storvold R,Eide HA,Stamnes K,Li W,Nieke J,Nakajima Y,Takahashi F,2007.ADEOS-II/GLI snow/ice products—Part II:Validation results using GLI and MODIS data.Remote Sensing of Environment,111:274-290.

Bourdelles B,Fily M,1993.Snow grain-size determination from Landsat imagery over Terre Adélie,Antarctica.Annals of Glaciology,17:86-92.

Brun E,Martin E,Simon V,Gendre C,Coleou C,1989.An energy and mass model of snow cover suitable for operational avalanche forecasting.Journal of Glaciology,35(121):333-342.

Cao MS,Li X,Chen XZ,Wang J,Che T,2006.Remote Sensing of Cryosphere.Science Press,China.

Clark RN,Roush T,1984.Reflectance spectroscopy:Quantitative analysis techniques for remote sensing applications.Journal of Geophysics Research,89:6329-6340.

Dobbins RA,Jizmagian GS,1966.Optical scattering cross sections for polydispersions of dielectric spheres.Journal of the Optical Society of America,56(10):1345-1350.

Domine F,Albert M,Huthwelker T,Jacobi HW,Kokhanovsky AA,Lehning M,Picard G,Simpson WR,2008.Snow physics as relevant to snow photochemistry.Atmospheric Chemistry and Physics,8:171-208.

Dozier J,Davis RE,Perla R,1987.On the objective analysis of snow microstructure,in Avalanche Formation,Movement and Effects.In:Gubler H(ed.).IAHS Publ.No.162,Int.Assoc.Hydrol.Sci.,Wallingford,U.K.,pp.49-59.

Dozier J,Marks D,1987.Snow mapping and classification from Landsat Thematic Mapper Data.Annals of Glaciology,9:97-103.

Fily M,Bourdelles B,Dedieu JP,Sergent C,1997.Comparison of in situ and Landsat Thematic Grain Mapper derived snow grain characteristics in the Alps.Remote Sensing of Environment,59(3):452-460.

Green RO,Dozier J,1996.Retrieval of surface snow grain size and melt water from AVIRIS spectra.In:1996 Airborne Geoscience Workshop.Jet Propulsion Laboratory,Pasadena,CA,pp.127-134.

Hyvärinen T,Lammasniemi J,1987.Infrared measurement of free-water content and grain size of snow.Optical Engineering,26(4):342-348.

Jiang TL,Zhao SH,Xiao PF,Feng XZ,Zhang Y,Hu W,2009.Spectral analysis of different snow grain sizes based on field measurement.Journal of Glaciology and Geocryology,31(2):227-232.

Jin ZH,Charlock TP,Yang P,Xie Y,Miller W,2008.Snow optical properties for different particle shapes with application to snow grain size retrieval and MODIS/CERES radiance comparison over Antarctica.Remote Sensing of Environment,112:3563-3581.

Jordan RE,1991.A one-dimensional temperature model for a snow cover:Technical documentation for SNTHERM.89.In:Special Report,91(16),U.S.Army Corps of Engineers,Cold Regions Research and Engineering Laboratory,Hanover,NH.

Kay JE,Alan RG,Hansen GB,Pettit EC,2003.Spatial relationships between snow contaminant content,grain size,and surface temperature from multispectral images of Mt.Rainier,Washington (USA).Remote Sensing of Environment,86:216-231.

Kokhanovsky AA,Zege EP,2004.Scattering optics of snow.Applied Optics,43(7):1589-1602.

Lesaffre B,Pougatch E,Martin E,1998.Objective determination of snow-grain characteristics from images.Annals of Glaciology,26:112-118.

Li W,Knut S,Chen BQ,Xiong XZ,2001.Retrieval of the depth dependence of snow grain size from near-infrared radiances at multiple wavelengths.Geophysical Research Letters,28(9):1699-1702.

Liang J,Wang J,2009.Hyperion hyperspectral image:Analysis and process.Journal of Glaciology and Geocryology,31(2):247-250.

Lyapustin A,Tedesco M,Wang YJ,Aoki T,Hori M,Kokhanovsky A,2009.Retrieval of snow grain size over Greenland from MODIS.Remote Sensing of Environment,113(9):1976-1987.

Mugnai A,Wiscombe WJ,1987.Scattering of radiation by moderately nonspherical particles.Journal of Atmosphere Sciences,37:1291-1307.

Nolin AW,Dozier J,1993.Estimating snow grain size using AVIRIS data.Remote Sensing of Environment,44:231-238.

Nolin AW,Dozier J,2000.A hyperspectral method for remotely sensing the grain size of snow.Remote Sensing of Environment,74:207-216.

Nolin AW,Stroeve JC,1997.The changing albedo of the Greenland ice sheet:Implications for climate change.Annals of Glaciology,25:51-57.

Painter TH,Molotch NP,Cassidy M,Flanner M,Steffen K,2007.Contact spectroscopy for determination of stratigraphy of snow optical grain size.Journal of Glaciology,53(180):121-127.

Painter TH,Rittger K,McKenzie C,Slanghter P,Davis RE,Dozier J,2009.Retrieval of subpixel snow covered area,grain size,and albedo from MODIS.Remote Sensing of Environment,113:64-77.

Sabol DE,Adams JB,Smith MO,1992.Quantitative subpixel spectral detection of targets in multispectral images.Journal of Geophysics Research,97:2659-2672.

Scambos TA,Haran TM,2007.MODIS-based Mosaic of Antarctica (MOA)data sets:Continent-wide surface morphology and snow grain size.Remote Sensing of Environment,111:242-257.

Stamnes K,Li W,Eide H,Aoki T,Hori M,Storvold R,2007.ADEOS-II/GLI snow/ice products—Part I:Scientific basis.Remote Sensing of Environment,111:258-273.

Stamnes K,Tsay SC,Wiscombe WJ,Jayaweera K,1988.Numerically stable algorithm for discrete-ordinate-method radiative transfer in multiple scattering and emitting media.Applied Optics,27:2502-2509.

Warren SG,Wiscombe WJ,1980.A model for the spectral albedo of snow.II:Snow containing atmospheric aerosols.Journal of the Atmosphric Sciences,37:2734-2745.

Wiscombe WJ,Warren SG,1980.A model for the spectral albedo of snow.I:Pure snow.Journal of the Atmospheric Sciences,37:2712-2733.

Zege E,Katsev I,Malinka A,Prikhach A,Polonsky I,2008.New algorithm to retrieve the effective snow grain size and pollution amount from satellite data.Annals of Glaciology,49(1):139-144.