空军作战仿真不确定区间数据处理方法研究

蒋天合 胡剑文

(空军指挥学院，北京100097)

1 引言

空军作战仿真过程需要多种数据作支撑，其中既有确定数据，也有大量不确定数据。传统的不确定数据研究以点状不确定数据研究为主，对具有一定范围的多维不确定区间数据研究还不多，探索基于证据理论的多维不确定区间数据研究方法对开展空军作战仿真具有一定的支持作用。

在空军作战仿真所需的数据中，由于采集、传输和技术手段等多种原因，很多数据具有明显的不确定性，如不同专家对同一问题的描述存在不一致性，不同探测装备因性能不同对同一目标的探测结果也具有不确定性。不确定数据通常以概率形式表达，如何将不同的概率数据组合在一起，形成服务于作战仿真的数据，成为作战仿真领域亟待解决的问题，证据理论可以较好地处理此类不确定数据的组合问题。

2 不确定数据产生的原因

空军作战仿真中不确定数据产生原因比较复杂，可能是原始数据本身不准确或是采用了粗粒度的数据集合方法，也可能是为了满足特殊应用目的或是在处理缺失值、数据集成过程中而产生，更多的情况是由于专家对同一问题的判断结果不一致或不同设备对同一现象的不同判断所导致［1］。

(1)采集的原始数据具有不确定性。首先，仪器采集数据的准确度受仪器本身的性能制约;其次，在网络传输过程中，数据的准确性受到带宽、传输延时、适配性等因素影响;最后，在传感器网络应用与RFID(无线射频识别)应用等场合，周围环境也会影响原始数据的准确度。

(2)粗细粒度数据集合相互转换过程中会产生不确定性。从粗粒度数据集合转换到细粒度数据集合的过程会产生不确定性，反之亦然。例如，假设某个记录飞机位置的数据以批次飞机坐标为记录目标，而仿真模型要求调用以单架飞机为目标的坐标数据，其结果必然存在不确定性。

(3)特殊应用目的产生不确定性。空军是高科技兵种，对作战进程影响较大，其装备性能和使用情况往往具有战略性质，为此很多资料属于保密范围，知情范围受限，数据需求单位只能以公开的内容进行估计，从而产生不确定性。如空军的某新型雷达探测性能数据只能进行粗略估算。

(4)缺失值处理产生不确定性。缺失值产生的原因很多，人员工作失误、装备故障、字段不一致、历史原因等都可能产生缺失值。插值、删除和人为填补所有含缺失值的记录是常用的处理方式，但这些操作在一定程度上影响数据准确度。

(5)数据集成过程中产生不确定性。空军作战仿真需要的数据来源广泛，有时存在数据标准不统一现象，特别是不同数据源可能在格式、内容、精度等方面存在不一致，在数据集成过程中会产生不确定性。

(6)不同专家对事物的判断存在不确定性。由于外界条件的限制或自身知识背景的不同，不同专家对某一事物的描述不能明确地给出确切结果，而是一个相对模糊的判断，如按概率给出肯定度、不确定度和否定度，此类结果数据在使用过程中必然存在不确定性。

无论何种原因产生的数据不确定性，在空军作战仿真过程中，都要按照模型的需要进行适当的处理，使之能够满足系统运行的要求。

3 基于证据理论的不确定数据处理方法

3.1 证据理论基本知识

主观概率定义为在描述不确定事物时，由人的主观因素所确定的概率，它与人的知识积累、个人偏好有关。其描述方法为:

P={(肯定)，(不确定)，(否定)}，P表示概率分布集合，其中，肯定是指对事物的肯定判定概率，否定是指对事物的否定判断概率，不确定指事物可能是肯定，也可能是否定，可解释为对事物一无所知。

主观概率分配具有以下关系，即:P(肯定)+P(不确定)+P(否定)=1

当肯定的概率为1时，表示事物是完全肯定的;当否定的概率为1时，表示事物是完全不可信的;当不确定的概率为1时，表示此判断毫无意义，即不是确定的，也不是否定的，专家对此问题完全一无所知。

定义1 设函数M:2D→［0，1］，且满足:

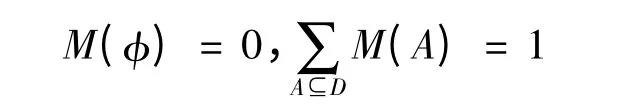
则称M是2D上的概率分配函数，M(A)称为A的基本概率数［2］。由于人的知识储备受限，因此，在实际工作中允许专家有一定的不确定概率，即对某一事物的理解存在一定程度的一无所知，将其概率分配空间设定为{(肯定)，(不确定)，(否定)}。由于不同背景的专家对同一事物可能产生几种不同的概率分配函数，需要对它们进行组合，证据理论的组合方法可对多个概率分配函数进行正交和运算。

定义2 设M1和M2是两个概率分配函数，则其正交和M=M1⊕M2为:

如果K≠0，则正交和M也是一个概率分配函数;如果K=0，则不存在正交和M，称M1和M2矛盾。

对于多个概率分配函数M1，M2，…，Mn，如果它们可以组合，则也可通过正交和运算将它们组合为一个概率分配函数。

定义3 设M1，M2，…，Mn是n个概率分配函数，则其正交和M=M1⊕M2⊕…⊕Mn为:

3.2 不确定区间数据的概率分配描述方法

传统的事物描述方法中，通常以确定数据给出结果，如在通过判读空军某次模拟对抗视频而收集作战数据的过程中，由三名专家判读模拟数据，对一次导弹攻击，甲、乙、丙分别给了不同的击中、未击中和不确定三个概率分配，由证据理论可直接进行数据组合，计算出组合后的概率分配情况。但在准备空军作战仿真数据过程中，很多情况下通常要将判断的结果描述为具有一定范围的数据，而不是某个确定的数值。不同的专家给出的数据范围通常具有一定的重合度，但又不一定完全重合，对此类情况证据理论通常不能直接应用。为此我们将专家给出的数据区域进行分割，对专家给出的概率进行重新分配，然后针对不同的区域分别利用证据理论进行组合，得出不同分割区域的概率分配，进而分析其数据，仍具有十分重要的意义。因此，首先定义区间数据。假设对给定的多维区间数据以D(N1，N2，…，Nn)来描述，其中每一维数据用一个范围描述，即Ni=(di1，di2)(i=1，2，…，n)，形成多区间数据，对此空间的整体描述可表述为D(M)，详细描述为((d11，d12)，(d21，d22)，…，(dn1，dn2))。对二维数据，其数据空间可描述为平面坐标内的一个面状区域，三维数据可描述为立体坐标空间的一个体积空间。

假设有N名专家对同一个事实进行判断，得出N个描述结果，为更加科学地表达现实的不确定性，专家们统一采用概率描述形式，即M(T，I，F)，其中T表示结果为肯定的概率，F表示结果为否定的概率，I表示结果为不确定的概率。以两名专家为例，采用二维平面数据描述同一现象，由于数据描述范围存在一定的交叉，其最多分割为三个区域，如图1所示。

图1 专家描述不确定区间数据示意图

图1 中，A、B表示专家的判断范围(为区别明显采用不同精细的实线)，1、2、3表示专家判断的范围相交后的分割区域。

以S1表示A被分割后的1部分面积，同理，S2、S3表示2、3部分的面积。对A专家的判断结果，1区域中的肯定概率T1与面积成正比，1区域中的否定概率为不落入整个A判断区域的否定概率与不落入1区域中的肯定概率(A)之和，不确定概率与整个判断的不确定概率相同。因此，对1区域的不确定数据概率计算规则如下:

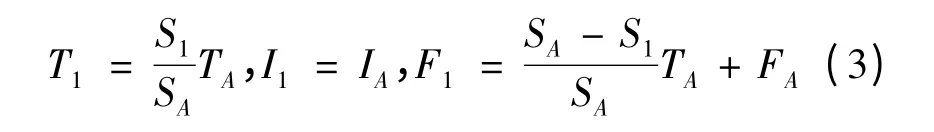
由二维推广到多维区间数据，其对不同分割部分概率计算方法如下:

式(4)中，Vi为被分割的第i个数据空间体积，V为某专家判断的数据区间体积。T、I、F分别为专家对个人判断结果的肯定、不确定和否定概率分配。

当一名专家的评判区域与其他专家的评判区域无交点时，则认为其他专家对此区域没有肯定的影响，但是其他专家自身评判的肯定会对其他区域产生否定的影响，对不相交区域的不确定影响概率为肯定概率之外的数值，计算方法为:

由分析可知，证据理论的三元组描述方法中，加入了不确定因素，成为区别于传统的非黑即白的概率判断标准。由于不确定因素的加入，可以看出对专家判断的每一个分割区域，其他专家的判断结果对每个分割区域均有不同程度的影响，即一名专家的不确定概率分配会对非本人判断的区域有一定的影响，其计算方式如下:Mi(肯定)=Ti，Mi(不确定)=Ii，Mi(否定)=Fi，其中i表示被分割的第i个区域，Ti表示不同专家对此区域作肯定判断的主观概率，Ii表示不同专家对此区域作不确定判断的主观概率，Fi表示不同专家对此区域作否定判断的主观概率，当分割区域属于某一专家的判断范围时，按式(3)、式(4)计算，当分割区域不属于某一专家的判断范围时，按式(5)计算，由此可分别计算每名专家对各个分割区域的主观概率影响。通过各专家对不同区域的概率影响计算，可以实现不同分割区域的概率影响组合计算。

3.3 不确定区间数据的概率组合计算方法

针对不同的分割区域，其概率分配计算过程如下:

(1)计算每个区域的面积;

(2)运用式(4)、式(5)计算专家对每个区域的概率影响;

(3)运用式(2)组合计算每个区域的概率分配;

(4)利用肯定概率与对应面积之比计算概率密度。

以图1为例，A、B专家对1区域的肯定概率分配影响为:

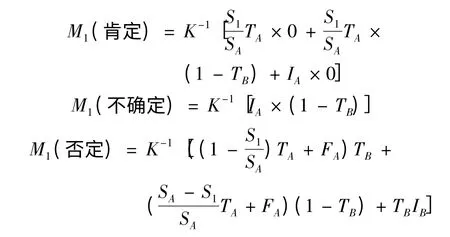
在一个数据空间内，不同的分割区域具有不同的概率分配，将概率与数据分割区域的体积进行比值运算，即为概率密度，是度量概率特征的一个重要指标。

4 应用示例

应用背景:空军作战仿真中，经常需要判断飞机的当前状态参数［3］。描述状态的参数有多种，如高度、速度、加速度、俯仰角、方向角等，为简化问题的复杂性，选取其中的高度和速度为示例，以二维数据描述，具体如下。

选取不同背景的三名专家，分别记为A、B、C，同时描述一架飞机，其主观概率互为独立，描述结果为:A(9000—9500m，700—720km/h)(0.8，0.1，0.1)、B(9100—9600m，720—740km/h)(0.75，0.15，0.1)、C(9200—9700m，740—760km/h)(0.85，0.1，0.05)，即三名专家的描述结果均为一个数值区间，三个区间具有一定的重合度，但又不完全重合，并且分别给出了专家的主观概率分配情况。为计算方便，设定每个范围的面积一样，分别归一化为边长为1的正方形，三名专家的评判标准互相影响，其分割情况如图2所示。

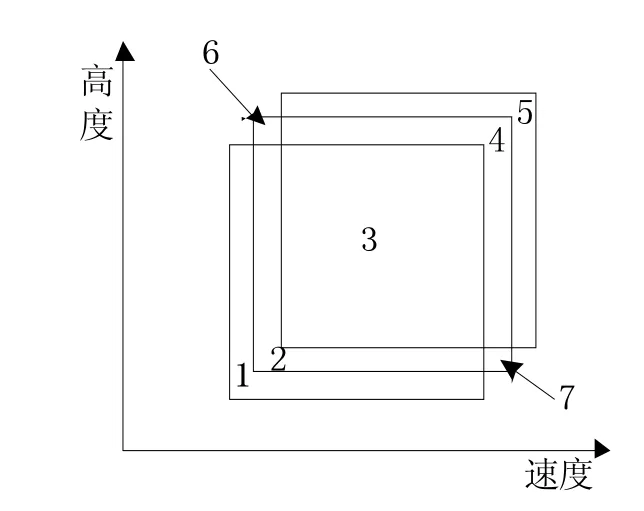
图2 区间数据分割块示意图

图2 中，最左边为专家A判断结果，中间为专家B判断结果，右边为专家C判断结果，三名专家的评判区域被分割为7块，分别用代号1—7表示。由于采用了三元组的概率分配描述方法，所以每个区域的实际概率分配受三名专家判断结果的影响，对每个区域可通过组合理论，可计算出不同区域的概率分配情况，按照上述提出的计算过程，分别计算不同分割区域组合后的概率分配结果，见表1。

根据证据理论组合方法，分别计算不同区域的组合后概率分配和肯定概率密度，结果见表2。

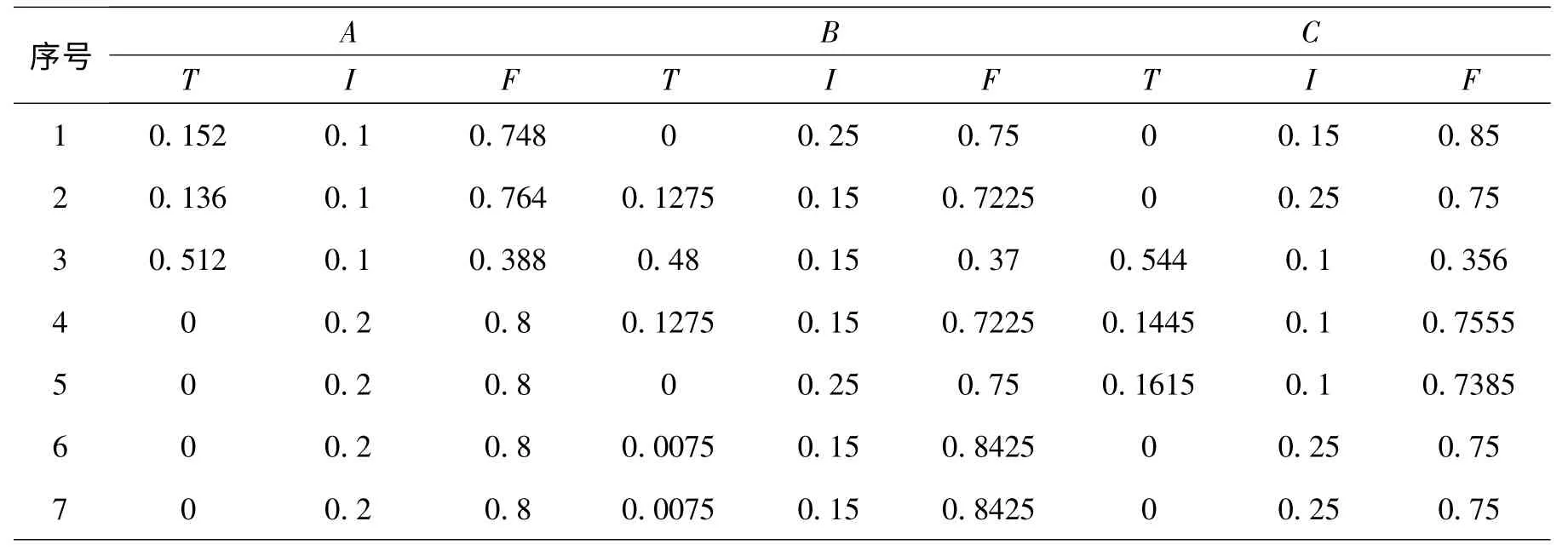
表1 不同专家的评判结果对每个分割区域的概率影响

表2 不同区域的组合后概率分配与概率密度

按照每个分割区域的肯定概率分配密度作柱状图，如图3所示。

图3 组合后的肯定概率密度对照

从图3中可以看出，三名专家判断区域的重合部分肯定概率明显高于其他区域。

5 结果分析

传统的证据理论概率分配空间可能很大，当因素较多时会产生组合爆炸问题，而文中分析的因素比较固定，其概率分配空间只有肯定、不确定和否定三种，用于对不同专家的判断结果可信性进行分析具有较强的适用性。由计算可知，基于证据理论的不确定区间数据分析方法，在处理多维的不确定区间数据时，特别是以一定范围描述的数据时，可以较好地解决不同专家的判断不一致问题。由计算结果可知，当专家的评判区域重合度较高时，重合区域的肯定概率明显高于非重合区域，可以推断出不同专家在评判过程中，能力相近的专家容易提高数据的肯定概率，形成一致意见。相反，意见分歧过大的专家评判结果，必然重合度低，则专家意见的肯定性越高越不利于形成统一意见，反而使数据更加不确定。当重叠区域的肯定概率达到规定标准时，则可据此做出有效决策。通过对不确定区间数据的处理，可以为空军作战实验提供较好的数据支撑［4］。

1 周傲英，金澈英，王国仁，等.不确定性数据管理技术研究综述［J］.计算机学报，2009(1):1-16.

2 金聪，郭京蕾.人工智能原理与应用［M］.北京:清华大学出版社，2009.

3 刘学军.论空军作战计划的不确定性研究［J］.空军军事学术，2004(6):54-56.

4 胡晓峰，胡剑文.面向信息化战争整体需求的探索性分析方法［J］.计算机仿真，2005，22(6):1-4.