基于社会网络分析的网络舆论系统状态研究

杨勇 薛振中

(武警警官学院，四川 成都610213)

1 引言

随着近年来互联网在我国的快速发展，基于互联网领域的群体性事件迅猛发展，影响范围不断加大。现实社会中的大量群体性事件由网络酝酿产生，并不断与网络产生互动，同时少数别有用心的人趁机煽动作乱，大量的网民盲目参与形成了难以控制的不安定局面，给党和政府对事件的妥善处置造成了干扰和压力。因此，深入研究与网络群体性事件密切关联的网络舆论系统，为下一步制定有效的防范策略带来新的思路，具有重要意义。

作为发展中的复杂系统学的一部分，国外一般把舆情形成与演化原理的研究划归于舆情动力学(Opinion Dynamics)范畴。从20世纪50年代Bibb Latané提出的社会影响理论(Social Impact Theory)开始，具有代表性的舆情动力学模型有:Sznajd模型(SM)、投票人模型(The Voter Models)、妥协模型(Relative Agreement)、多数准则模型(The Majority Rule Models)、Axelrod模型(又称文化模型)、受限信任模型(Bounded Confidence Model，BCM)等［1-6］。这些模型的研究对象主要是传统舆论，多数都使用基于主体的建模方法(Agent-Based Modeling)。但由于网络舆论系统的复杂性与社会性等特征，以规则确定行为的传统社会动力学原理难以适用。社会网络分析(Social Network Analysis，SNA)方法用社会网络结构对行动的限制来解释行为，是一种研究社会成员或群体之间的相互作用关系的有效方法。它将系统成员或成员群体间的关系作为研究对象，利用关系模型的特征参数进行量化分析，将定性研究与定量研究结合起来，比传统的定性研究更具优势。这一方法经过七十余年的反复验证和逐步完善已经成熟，已广泛用于社会学、心理学和经济学等学科领域的研究。

2 基于SNA的网络舆论系统状态参数差分法

通过对网络整体及网民主体的SNA属性参数组的差分计算获得网络舆论系统状态分布的变化量，通过差分量的时间序列展开观测状态变化是否符合预期，发现对状态分布和变化起主导作用的意见领袖，挖掘出网络舆论系统演化特征并对其进行定量分析，可以揭示出网络舆情事件的一般演化规律。

2.1基本步骤

(1)针对某一话题或某一关键词对关注中的网站或论坛进行数据采集，将采集到的数据进行初步的去噪消重处理，找出网民之间的回复关系，存入数据库。

(2)根据网络舆论持续时间或者状态观测者的要求设定观测周期Δt，该观测周期可随时进行调整。读取数据库中的数据，建立每个观测周期内的回复关系矩阵并绘制出网络社群图。

(3)根据网络社群图，计算出每个观测周期的SNA参数值。

(4)将每个观测周期的SNA参数值按时间序列展开，利用差分法计算每个观测周期内的SNA参数增量。

(5)对计算出的SNA参数增量进行综合分析研究，揭示出该网络舆论的特征。

2.2 网络舆论主体的状态分析

2.2.1 点度中心度与中心性

中心性是指个人或组织在其社会网络中具有怎样的权利，或者说居于怎样的中心地位。点度中心度是识别意见领袖的重要指标。一般认为，在网络中点度中心度最大的网民为该话题的意见领袖。

定义1 绝对点度中心度CADi，为与结点i有直接联系的结点数目，即与该网民发生直接联系的网民数目，主要反映该网民的影响范围。

定义2 相对点度中心度CRDi，为结点i的绝对点度中心度与图中点的最大可能度数之比，即与该网民实际发生直接联系的网民数目与最大可能发生直接联系的网民数目之比。在单向连接中的计算公式为:

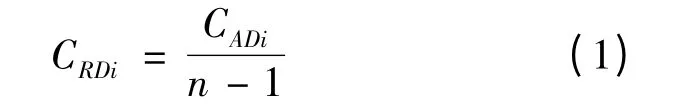
式(1)中，n为网络结点数，即网民数。CRDi以CADi为基础，主要反映该网民在整个网络中的核心性，即地位的中心程度。

2.2.2 基于时间序列的状态变化计算方法

设CADi(t)为t时刻网络结点i的绝对点度中心度，则一个采样周期Δt内CADi(t)的变化量为绝对点度中心度增量，记为ΔCADi(t)。

设CRDi(t)为t时刻网络结点i的相对点度中心度，则一个采样周期Δt内CRDi(t)的变化量为相对点度中心度增量，记为ΔCRDi(t)。

2.2.3 状态分析

记Δn(t)为网民数增量，当Δn(t)、ΔCADi(t)与ΔC'ADi(t)分别为正值、负值或0值时，其揭示出不同的网络舆论特征。下面将上述三个参数值简化为非负值与负值两种情况，分别进行研究，结果见表1。

对Δn(t)、ΔCRDi(t)与ΔC'RDi(t)分非负值与负值两种情况进行研究，结果见表2。

2.3 网络舆论系统的状态分析

表1 绝对点度中心度相关参数变化含义

表2 相对点度中心度相关参数变化含义

2.3.1 网络密度

网络密度表示网络社群图中各个结点间联络的稀密程度。在网络舆论系统中，结点表示发帖或跟帖的网民，结点间的连线表示网民间的帖子跟随关系，网络密度则反映出网民之间相互跟帖关系的密集程度。计算公式为:

式(8)中，n为网络结点数，即网民数;L为所有结点间实际拥有的连线数。

2.3.2 网络中心势

网络中心势以点度中心度为基础，刻画网络社群图的整体中心性，用来测量整个网络的连通情况对少数行为者的依赖程度。在网络舆论系统中用来测量信息流在整个网络的传播情况对少数网民的依赖程度。网络中心势反映的是网络社群图的整体向心程度，在网络舆论系统中则反映出其他网民对某一网民回应的集中程度。网络中心势越大，说明该话题的讨论集中程度越大，意见领袖具有的凝聚力越大，产生影响力较大的意见领袖的可能性越大。其数学表达式为:

由于当且仅当网络为包含n个结点的星形结构时，除数达到最大值n2-3n+2，因此，式(10)可以简化为:

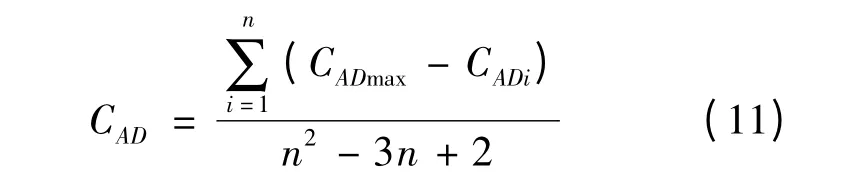
2.3.3 基于时间序列的状态变化计算方法

设D(t)为t时刻的社会网络密度，则一个采样周期Δt内D(t)的变化量为密度增量，记为ΔD(t)，ΔD(t)∈［-1，1］。

设C(t)为t时刻的社会网络中心势，则一个采样周期Δt内C(t)的变化量为网络中心势增量，记为ΔC(t):

网络中心势变化速度为:

2.3.4 状态分析

记Δn(t)为网民数增量，当Δn(t)、ΔD(t)与ΔD'(t)分别为正值、负值或0值时，其揭示出不同的网络舆论特征。下面将上述三个参数值简化为非负值与负值两种情况，分别进行研究，结果见表3。

对Δn(t)、ΔC(t)与ΔC'(t)分非负值与负值两种情况进行研究，结果见表4。

将ΔCADi(t)、ΔCRDi(t)、ΔD(t)和ΔC(t)称为SNA参数增量，将Δ(t)、Δ(t)、ΔD'(t)和ΔC'(t)称为SNA参数变化速度增量。一般而言，若网民数增量与SNA参数增量均大于0，说明网络舆论处于形成或发展时期，网络舆论具有进一步发展甚至爆发的可能，此时应予以重点关注;若网民数增量与SNA参数增量均小于0，则说明网络舆论处于回落或冷却时期，将逐渐退出公众的视野;若网民数增量、SNA参数增量与SNA参数变化速度增量在正负值之间围绕0波动，则说明参与者相互关系的密集程度和讨论的热烈程度有波动，网民对话题的关注度可能偏移或转移，网络舆论处于起伏状态，可能演变至偏移期或振荡期。

3 实验验证

以天涯论坛(www.tianya.cn)的“华南虎事件”为实验数据(该事件源于网络，并引发现实社会的大量关注)，运用SNA理论及其参数差分法，通过网络数据采集与分析系统实现对网络舆论状态观测方法的仿真。

3.1 实验数据

在2007年底至2008年初，华南虎事件是社会舆论的热点话题。该事件是网络舆论从发生、发展到爆发直至消亡的典型案例。据统计，该话题在天涯论坛上的总参与人数为5779人，总回帖数65029个，持续时间自2007年10月15日楼主发帖开始，直至2008年1月30日最后一位跟帖者发帖结束，经历了从形成、发展、爆发直至回落的主要演变过程。将回帖采集并经初步处理后存入数据库中，设定采样周期为1天，按天统计网民数，如图1所示。

表3 社会网络密度相关参数变化含义

表4 网络中心势相关参数变化含义

图1 天涯论坛“华南虎事件”舆论演变图

表5 SNA参数表(8天)

表6 SNA参数增量表(8天)

3.2 数据分析

将参与天涯论坛“华南虎事件”讨论的网民及其之间的联系看作是一个网络舆论系统。使用SNA方法进行数据分析，得到SNA参数值见表5(限于篇幅，仅截取11月15日—22日共8天数据)，其中CADi(t)、CRDi(t)分别为意见领袖的绝对点度中心度和相对点度中心度。通过分析这些参数值就可以了解到该网络舆论系统的主要特征。

根据上述SNA参数值，采用差分分析法计算其增量，见表6。

3.3 结论

通过数据分析，可以得出以下结论。

(1)11月16日，网民数量达到最大值，说明此时参与该话题讨论的人数最多，可认为是讨论最热烈的时刻。ΔCADi(t)与ΔC'ADi(t)也在同时达到最大值，这是符合预期的，体现出参与讨论的网民对于楼主的回复十分热烈且这种趋势大幅上升。但此时ΔCRDi(t)与Δ(t)为负，说明随着参与讨论的网民数量的增多，并非所有参与讨论的网民都回复楼主，网民之间也产生了一些讨论与交流，形成了一些小团体，即所谓的凝聚子群。在这些凝聚子群中，也有各自的意见主导者，随着舆情事件的演变，有成长为新意见领袖的可能。ΔC(t)与ΔC'(t)也达到最大值，说明当前时刻对于该话题的讨论集中程度大，当前意见领袖的凝聚力和影响力大，且这种趋势大幅上升。另一方面，由于参与网民数量激增，网民之间讨论交流不够充分，相互关系的密集程度大大减小，导致ΔD(t)大幅下降，但这种趋势有所下降。

(2)11月17日—24日，参与网民数量逐渐减少，舆情事件在经过爆发后开始回落。ΔCADi(t)为负值，说明讨论人数持续减少;Δ(t)出现最小值后围绕0值波动，说明这种趋势在大幅震荡后逐渐趋于平缓，这是舆情事件进入回落阶段的标志之一。ΔCRDi(t)与Δ(t)、ΔC(t)与ΔC'(t)均围绕0值小幅波动，说明网民之间讨论与交流更加热烈，趋势也有所反复。参与网民不再是单纯回复楼主，其间形成了一些凝聚子群，根据凝聚子群中意见主导者地位及其凝聚力和影响力的变化，楼主的意见领袖地位及其凝聚力和影响力也随之波动。ΔD(t)与ΔD'(t)在快速回落后基本保持不变，说明舆情事件在经过短暂的爆发期后，参与网民相互之间对该话题讨论的密集程度基本不变，趋势也基本保持稳定。

(3)11月25日—12月13日，网民数量保持稳定，这些网民是该话题较为稳定的参与者和讨论者。同时，ΔCADi(t)与Δ(t)、ΔD(t)与ΔD'(t)也保持稳定，这是舆情事件进入平稳阶段的标志之一。但是，ΔCRDi(t)与Δ(t)、ΔC(t)与ΔC'(t)均出现较大幅度的波动，说明网民间的讨论与交流仍然十分热烈，趋势也有较大幅度的变化，随时都有再次爆发或形成新意见领袖的可能，该舆情事件仍具有一定的生命力。

可见，通过对SNA参数增量与SNA参数变化速度增量的综合分析，能够在一定程度上揭示出网络舆论系统的深层次特征。

4 结束语

本文仅从系统整体的角度，借助SNA理论对网络舆论系统进行了研究，其中的许多细节尚有待进一步深入研究，如:网民主体的相关属性、网络舆论系统的相关属性、网络舆论系统的指标体系等。

1 SZNAJD WERON K，SZNAJD J.Opinion evolution in closed community［J］.International Journal of Modern Physics C，2000，11(6):1157-1165.

2 PETER CLIFFORD，AIDAN SUDBURY.A model for spatial conflict［J］.Biometrika，1973，60(3):581-588.

3 DEFFUANT G，NEAU D，AMBLARD F，et al.Mixing beliefs among interacting agents［J］.Adance in Complet Systems，2001(3):87-98.

4 GALAM S.Minority opinion spreading in random geometry［J］.Eur.Phys.J.B，2002，25(4):403-406.

5 AXELROD R.The dissemination of culture:A model with local convergence and global polarization［J］.Journal of Conflict Resolution，1997，41(2):203-226.

6 HEGSELMANN R，KRAUSE B U.Opinion dynamics and bounded confidence models，analysis，and simulation［J］.Journal of Artificial Societies and Social Simulation，2002，5(3):1-33.

7 STAUFFER D，SOUSA A O，OLIVEIRA S M.Generalization to square lattice of Sznajd sociophysics model［J］.International Journal of Modern Physics C，2000，11(6):1239-1245.

8 BERNARDESA T，STAUFFER D，KERTFFESZJ.Election results and the Sznajd model on Barabasi network［J］.European Physical Journal B，2002，25(1):123-127.

9 GONZALEZ M C，SOUSA A O，HERRMANN H J.Opinion formation on a determinstic pseudo-fractal network［J］.International Journal of Modern Physics C，2004，15(1):45-57.

10 FORTUNATO S.The Krause Hegselmann consensus model with discrete opinions［J］.International Journal of Modern Physics C，2004，15(7):1021-1029.

11 HOLME P，NEWMAN M E J.Nonequilibrium phase transition in the coevolution of networks and opinions［J］.Physical Review E，2006，74(5):1-5.

12 KOZMA B，BARRAT A.Consensus formation on adaptive networks［J］.Physical Review E，2008，77(1):6102-6114.

13 张立，刘云.网络舆论传播的无标度特性及其衰减模型的研究［J］.北京交通大学学报:自然科学版，2008，32(2):67-70.

14 曾祥平，方勇，袁媛，等.基于元胞自动机的网络舆论激励模型［J］.计算机应用，2007，27(11):2686-2688，2714.