基于响应曲面法的铣削参数优化

王磊，刘巧，梅卫江，朱红波，朱培根

(1. 石河子大学机械电气工程学院，新疆石河子832003;2. 石河子大学信息科学与技术学院，新疆石河子832003)

随着现代工业化的迅猛发展，如何提高产品性能、缩短生产周期已成为目前机械制造业的关键问题。产品的性能与零件的整个加工过程联系紧密，而保证零件切削加工质量、提高切削加工效率是其中至关重要的一环［1］。要提高加工工件的精度，使其达到应用要求，就要合理选择机床、刀具材料、工艺路线及切削参数。但在机械加工过程中，影响加工质量的因素很多［2］，而且因素之间也是相互影响、相互制约的。特别是切削三要素［2－3］，它们对零件表面质量影响很大。而回归正交设计法［4－5］借助于组合设计的思想，是回归分析与正交试验设计法有机结合形成的一种新的试验设计法。它分一次回归正交设计和二次回归正交设计。二次正交旋转组合设计是根据正交性与旋转性从全名试验中挑选出具有代表性的点进行试验，是研究多因子多水平的一种高效、经济的试验设计方法。这种方法不但试验规模小、计算简便，而且与试验中心点距离相等的球面上各点回归方程预测值的方差相等。响应曲面法［6］是根据正交旋转中心复合设计［7］所得到的。因此，作者应用二次正交旋转组合设计试验方案，利用试验分析得出铣削工艺参数对表面粗糙度的回归模型，利用响应曲面法的等值线和响应曲面图，直观分析各切削要素对表面粗糙度值的影响规律，从而为实际加工中切削参数的选择提供理论依据。

1 试验装置和试验方法

1.1 试验装置

试验中使用的直径12 mm 的高速钢直柄三刃立铣刀，铣刀规格为12 × 12 × 26 × 83，刀柄规格为BT40。采用DM4600 立式镗铣加工中心，主轴转速为50 ～6 000 r/min，切削进给率可达1 ～5 000 mm/min，分辨率可达0.001 mm，切削深度为18 mm。

1.2 试验方法

根据实验目的确定实验方案，选取铣削切削要素中的主轴转速、进给速度、切削宽度3 个因子进行多因子试验，以表面粗糙度值作为性能指标，按三因子五水平安排试验，制定的因子水平编码表如表1所示。

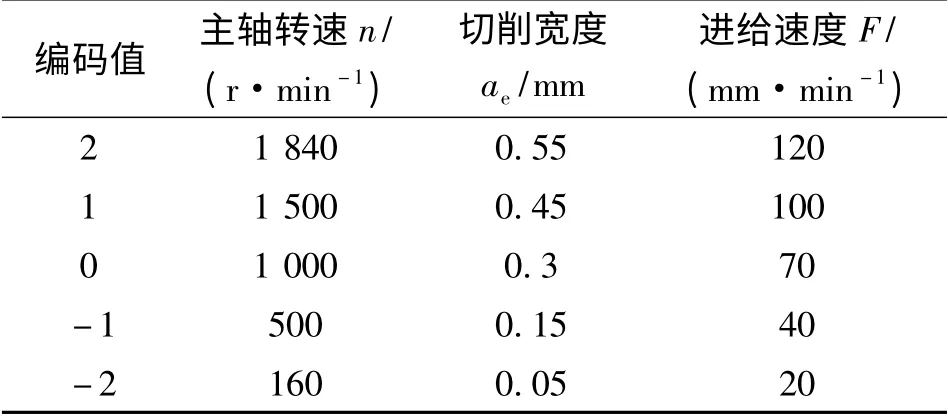
表1 因素水平表

1.3 表面粗糙度与切削要素的关系试验

通过试验，利用9J 光切显微镜［8］测得表面粗糙度Rz值。试验实施过程分为两个阶段:第一阶段按L8(27)实施，即表中前8 个组合因素进行正交试验分析，结果如表2 所示。其目的是对切削要素对表面粗糙度影响程度及影响规律进行初步分析;若分析显示各因素对指标影响呈非线性关系，则进行第二阶段，即后续试验，以满足寻优及建立非线性回归模型之需要。

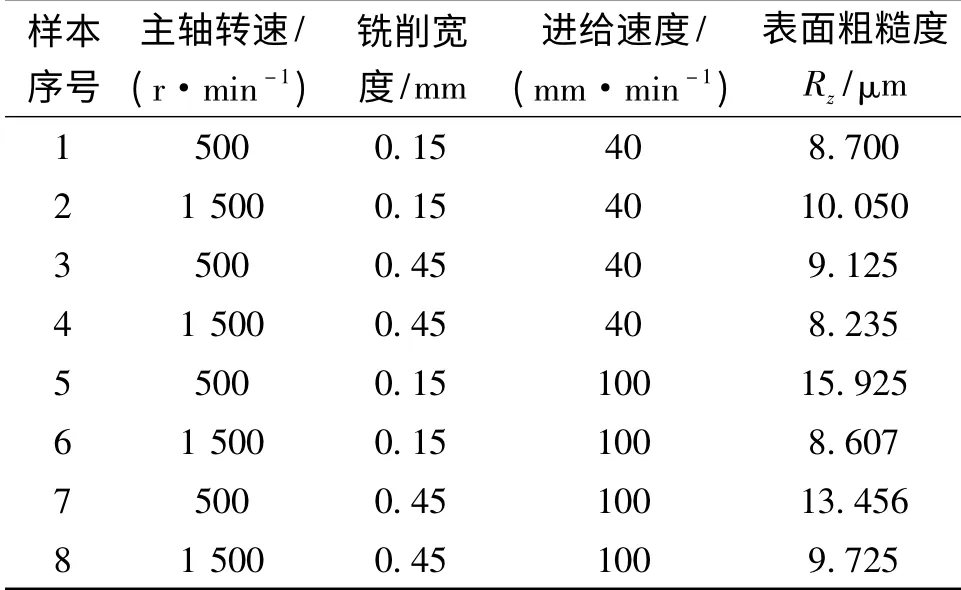
表2 各因子对表面粗糙度的前8 组试验结果

根据表2 的试验数据，应用Minitab 软件对前8组数据进行分析，给出各因素及其交互效应分析结果，同时给出响应曲面，结果如图1 所示。

图1 表面粗糙度的曲面图

图1 显示主轴转速与切削宽度、进给速度与切削宽度对表面粗糙度的影响呈线性关系，而主轴转速与进给速度对表面粗糙度的影响呈非线性关系，则需进行第二阶段，即后续试验，试验结果如表3 所示。

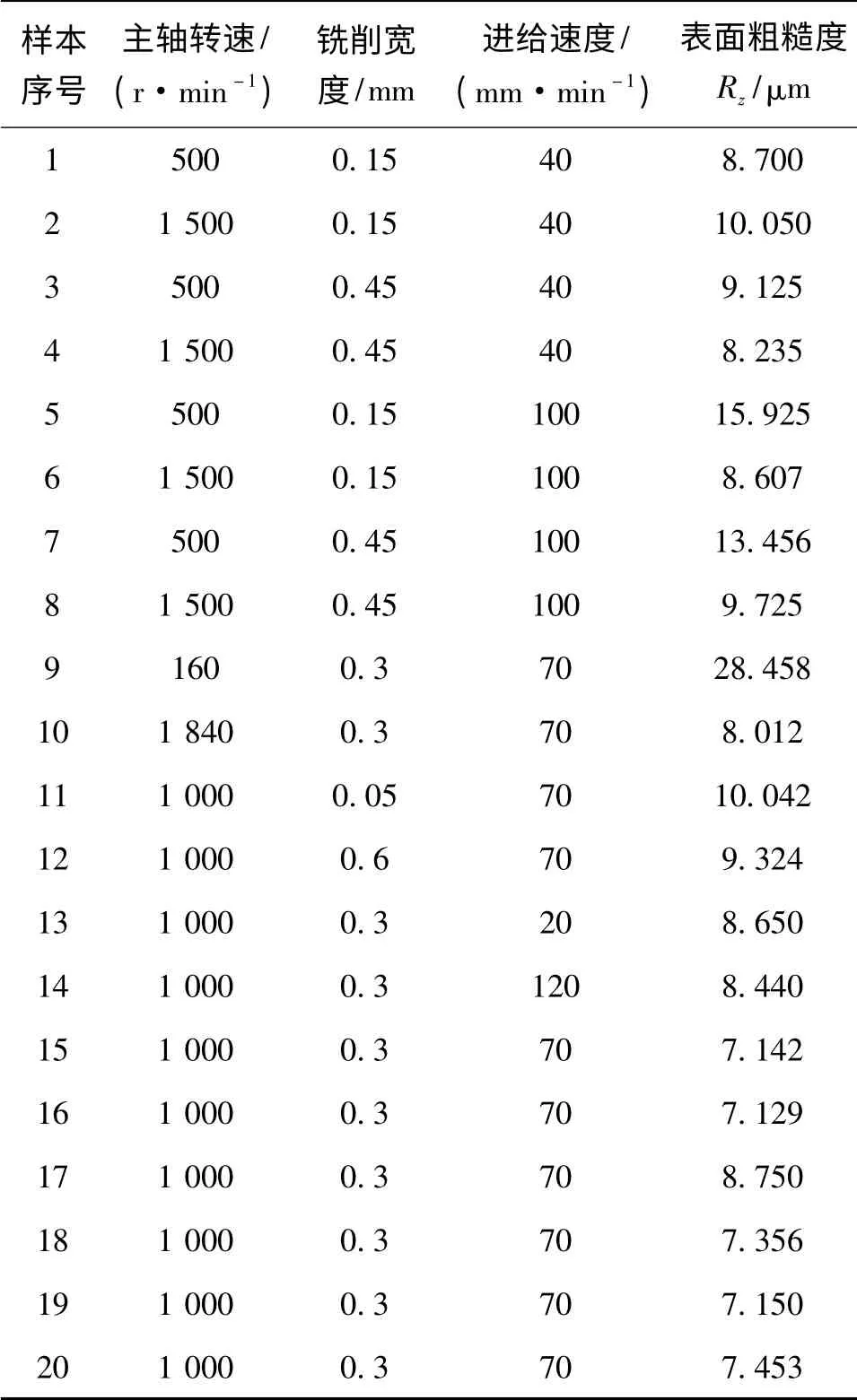
表3 各因子对表面粗糙度的试验结果

2 试验结果分析

根据表3 的试验数据，应用Minitab 软件得出切削要素对表面粗糙度的统计分析结果，见表4。

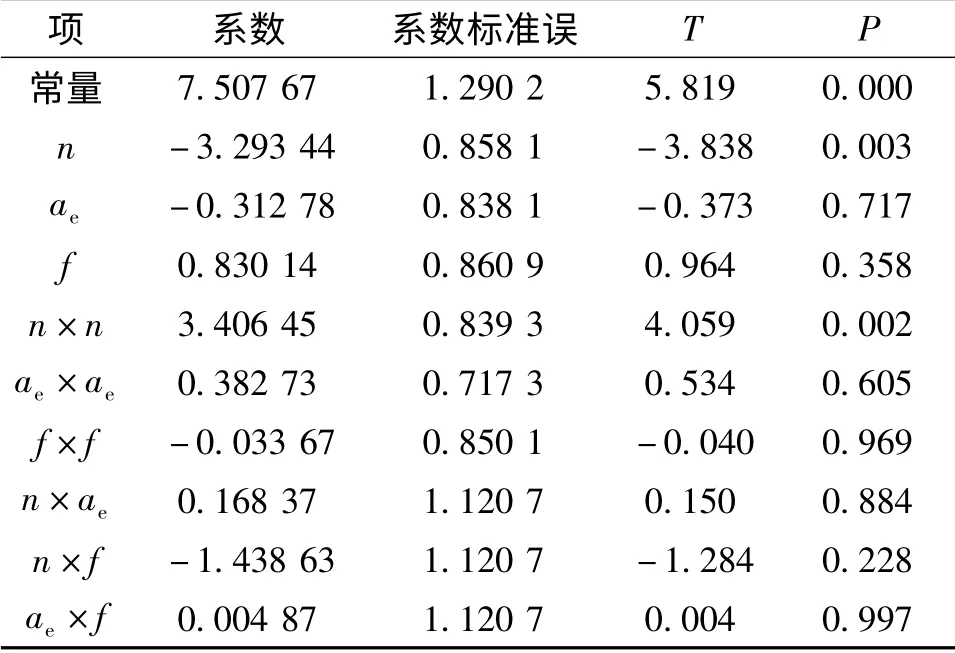
表4 表面粗糙度的估计回归系数

表4 给出了模型中所有项的回归系数。因为使用了正交设计，所以需要单独估计每个效应。因此，线性项的系数与拟合线性模型时相同，由于减少了误差导致的变异性，因此误差项S =3.169 7 变小。这表明，实际数据点到回归线(预测值)的标准距离为3.169 7 μm。同时从结果中可以看出f × f 的P 值为0.969、ae×f 的P 值为0.997，这两个指标为不显著指标，因此将其剔除后得到R － Sq(调整) =63.06%。

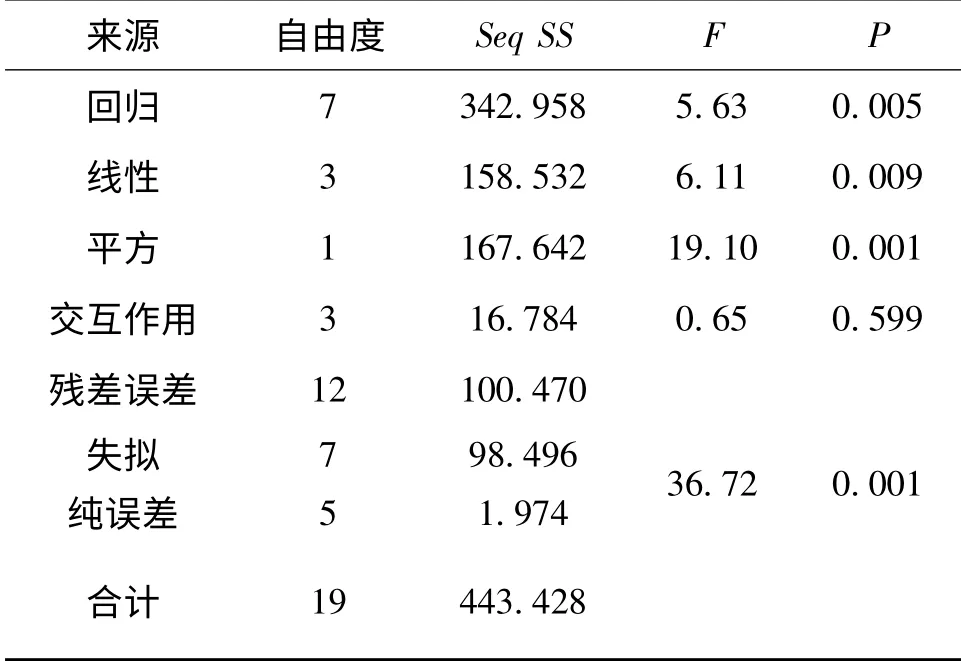
表5 表面粗糙度Rz (μm)的方差分析

显著性值小于0.05 时，模型显著。通过表5 确定在该情况下，回归、线性、平方以及失拟是有效模型。主轴转速与主轴转速的平方的P 值均小于0.05，因此主轴转速与主轴转速的平方为影响表面粗糙度的重要项，从而可以得知主轴转速对表面粗糙度的影响最大。

通过上述分析，可得表面粗糙度Rz(μm)的估计回归系数为:

图2 的表面粗糙度标准化残差直方图表示，3 号点为表面粗糙度的异常值。标准化残差正太概率图显示的基本为一条直线，因此原有假设是合理的。

图3 表面粗糙度与铣削宽度、主轴转速等值线与响应曲面图显示:当主轴转速为1 000 r/min，切削宽度对表面粗糙度的影响较小，为表面粗糙度最好点，当主轴转速以1 000 r/min 为中心点增加或者减少时，表面粗糙度值均会增大，且在主轴转速降低的情况下，由于等值线较密集，因此表面粗糙度值的变化较为显著。而随着切削宽度从中心点增加或减少等值线基本呈线性变换，因此切削宽度对表面粗糙度的影响不显著。

图2 表面粗糙度的残差图

图3 表面粗糙度与铣削宽度、主轴转速的等值线与响应曲面图

表面粗糙度与进给速度、铣削宽度等值线与响应曲面图(图4)显示:当进给速度从该试验方案选取的最小值20 mm/min 增大时，测得的表面粗糙度值呈线性增大的趋势;同时切削宽度从0.05 mm 增大时，表面粗糙度也呈线性变化。因此，进给速度、切削宽度对表面粗糙度的影响不显著。

图4 表面粗糙度与进给速度、铣削宽度的等值线与响应曲面图

表面粗糙度与进给速度、主轴转速的等值线与响应曲面图(图5)综合反映了图4、图5 所显示的结果。当主轴转速以1 000 r/min 为中心点增加或者减少时，表面粗糙度值增大，而在主轴转速降低的情况下表面粗糙度的等值线变化较为密集，因此主轴转速降低的情况对表面粗糙度的影响较为显著;当进给速度从20 mm/min 增大时，表面粗糙度值呈线性增大趋势。可得出在主轴转速较低、进给速度较大的时候，表面粗糙度的变化最为明显。

图5 表面粗糙度与进给速度、主轴转速的等值线与响应曲面图

3 试验优化

铣削加工工艺参数优化的目标有很多种，文中以提高表面加工质量为优化目标。根据表面粗糙度的要求，采用响应曲面参数优化，利用Minitab 软件进行优化求解。加工过程中的约束包括机床、刀具和工件的约束，在该试验中分别将主轴转速、切削宽度、进给速度作为约束条件 (如表6 所示)，进行模型优化，寻找到最满足性能指标的因子最佳组合，得到以下结果:

表6 约束条件

起始点为:n=1 000 (r/min);ae=0.3 (mm);f=70 (mm/min)。

全局解为:n = 1 178.37 (r/min);ae=0.047 731 1 (mm);f= 19.546 2 (mm/min)。

预测的响应为:表面粗糙度Rz=5.848 61 μm;合意性=1.000;复合合意性=1.000。

从图6 中可知:主轴转速过高和过低都不利于表面粗糙度的减小，且影响较大;随着进给速度和铣削宽度的增大，表面粗糙度也随之增大，但影响不显著。

按照上述结果找出最佳的操作条件以使表面粗糙度值较小并使振动特性参数较大，最后得到一组最优参数:主轴转速 1 178.37 r/min、铣削宽度0.047 731 1 mm、进给速度19.546 2 mm/min。在实际加工中，选取主轴转速为1 180 r/min、铣削宽度为0.05 mm、进给速度为20 mm/min，得到的表面粗糙度为5.848 61 μm，比期望值提高了20%，从而大大提高了零件加工表面质量。

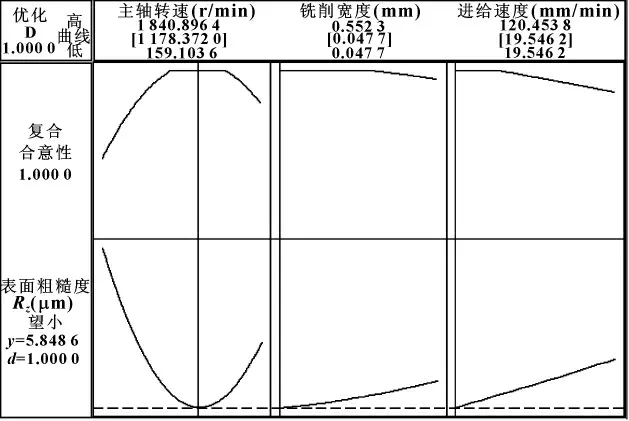
图6 切削参数优化图

4 结论

采用二次正交旋转组合试验设计方法对铣削加工工艺参数对表面粗糙度影响进行实验研究，对表面粗糙度实验数据进行分析和处理，确定主轴转速以及主轴转速的平方项均对表面粗糙度的影响较为显著，并建立了表面粗糙度的回归模型，经方差分析，回归模型方程高度显著。通过响应曲面分析得到的等值线和响应曲面图可非常直观地看出各铣削工艺参数与表面粗糙度之间的相互关系，可为实际生产中铣削工艺参数的合理选择提供理论依据。

【1】郭杰.基于虚拟仪器的切削振动监测与分析系统的研究［D］.南京:南京航空航天大学，2006.

【2】孙成豪.基于表面粗糙度的铣削加工切削参数选择方法研究［D］.济南:济南大学，2010.

【3】焦士仲. 金属切削原理［M］. 北京:机械工业出版社，1991.

【4】陈洪涛.数控加工工艺与编程［M］.北京:高等教育出版社，2006.

【5】李学光，王惠伟，张树仁，等.基于正交试验法的切削参数优化研究［J］.机床与液压，2011，39(8):17 －19.

【6】任露泉.试验优化设计与分析［M］.长春:吉林科学技术出版社，2001.

【7】袁人炜，凡孝勇，曲征洪.基于响应曲面法的铣削力建模实验研究［J］.工具技术，2000(S1):22 －24.

【8】韩秋实，王红军.机械制造技术基础［M］.北京:机械工业出版社，2005.