基于D-S 理论和AMESim 技术的液压缸泄漏故障诊断仿真研究

蔡伟，徐文华，李慧

(第二炮兵工程大学二系，陕西西安710025)

泄漏是液压缸的常见故障之一，可分为外泄漏和内泄漏两种。传统的外泄漏检测方法往往采用是通过肉眼观察缸体外部及连接处是否有油液渗出来判定是否有外泄漏，或者将液压缸进行拆解以检测是否有内泄漏发生。这些方法存在着操作复杂、存在安全隐患等问题。近年来新发展的非介入式检测技术能够在不对设备进行拆解的条件下，实现装备状态信息的获取，有效地解决了测试安全性隐患，但同时存在测试精度不高的问题，影响了诊断结果可信度。

D-S 理论是针对事件发生后的结果探求事件发生的主要原因。对于具有主观不确定性判断的多属性诊断问题，D-S 理论是一种融合主观不确定性信息的有效手段。在液压缸泄漏故障诊断中，可利用故障状态下的压力、流量及活塞杆行程信息去探求液压缸的具体故障类型。

作者首先在理论上论证D-S 理论在液压缸泄漏故障诊断中应用的可行性，之后利用AMESim 软件对液压缸在正常工作及发生内、外泄漏故障等不同状态下的压力、流量和活塞杆行程信号进行仿真，实现D-S理论在泄漏故障诊断方面的实际应用。

1 建模仿真软件AMESim

AMESim®软件是IMAGINE 公司于1995 年推出的专门用于液压/机械系统的建模、仿真及动力学分析的软件。在液压系统仿真过程中，可以达到以下要求:

(1)可仿真液压缸正常状态及内泄漏状态;

(2)可得到不同状态下液压缸进油腔压力、进出油腔压力差以及活塞杆行程数据。

2 信度函数分配及数据融合

利用传感器获取的信息中不仅包含对各类故障的支持度，也将引入一定的不确定性。信度函数分配就是针对传感器输出信息中的支持度和不确定性进行量化，其计算公式为:

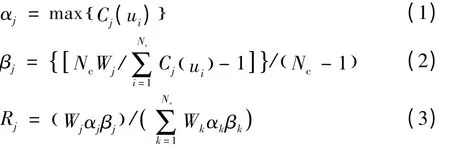
式中:Cj(ui)是传感器j 对目标模式ui的相关系数，其中i=1，2，…，Nc;Nc为目标模式数目，且必须大于1;Ns是传感器总数;Wj是传感器j 的环境加权系数，介于0 到1 之间;αj是传感器j 的最大相关系数;βj是传感器j 的相关分配值;Rj是传感器j的可靠性系数。

传感器j 对目标模式ui的信度函数为:

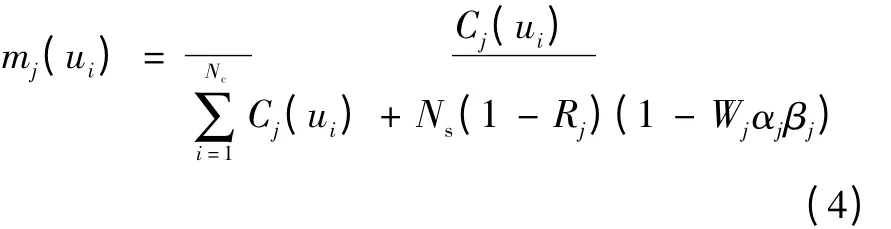
传感器j 的不确定性θ 的信度函数为

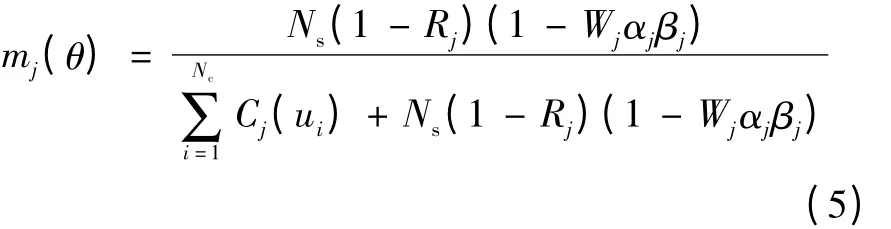
多传感器数据融合有3 种基本方法: (1)直接进行传感器数据融合; (2)以特征向量表示传感器数据，然后进行特征向量融合; (3)对每个传感器数据进行处理，获得高层推论或决策，然后进行决策级融合。作者采用的是决策层融合中的D-S 数据融合方法。

在液压缸的进油腔和出油腔分别设置超声波流量传感器S1 和S2，并利用S1-S2 获取液压缸进出油腔的流量差信号;在进油管设置超声压力传感器S3，获取液压缸进油腔的压力信号;在液压缸外侧设置伸缩式位移传感器S4，测量液压缸活塞杆行程。

设液压缸故障域为:u1表示液压缸内泄漏，u2表示正常状态，u3表示液压缸外泄漏，不确定性由θ表示。

经信度函数分配后得到各类传感器对内、外泄漏及不确定性的信度函数分别为:

首先对传感器S1-S2 和S3 的数据进行数据融合:

由公式(9)得到第一步数据融合结果:

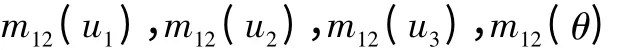
再和传感器S4 的数据进行融合:

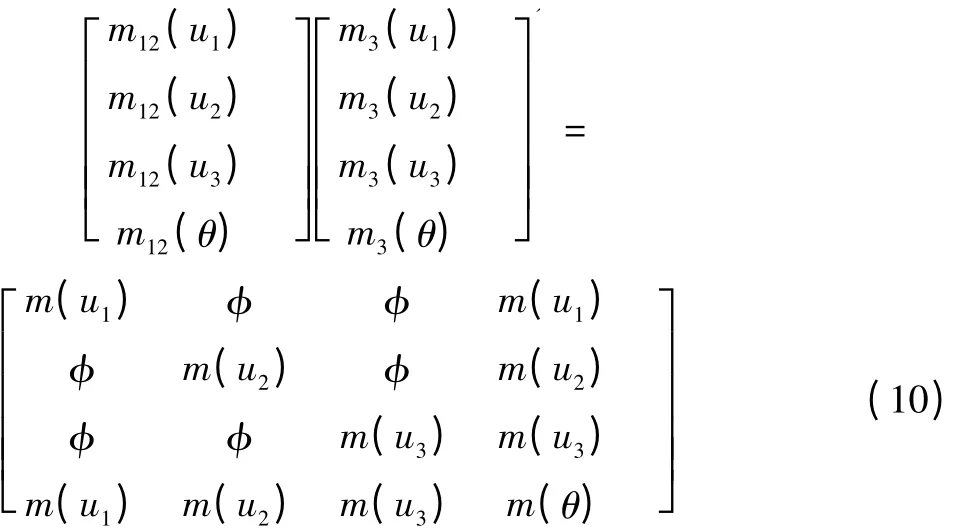
由公式(10)得到第二步的融合结果，也就是最终的融合结果:

3 仿真过程

液压系统仿真模型如图1 所示，在草图下搭建其模型结构，在子模型模式下为每个模块选取子模型，在参数模式下设置参数:发动机转速设置为1 480 r/min;泵的排量设置为63 mL/r，转速设置为2 000 r/min;三位四通换向阀各路流量设置为90 L/min，压降设置为0.01 MPa，阻尼比设置为0.8，阀芯固有频率设置为50 Hz，额定电流设置为200 mA;活塞直径设置为25 mm，活塞杆直径设置为15 mm;液压缸内泄漏状态下设置为5 L/ (min·MPa);外泄漏设置的节流阀流量设置为5 L/ (min·MPa);三位四通换向阀信号源设置为常数50。其他参数均按默认值设置。

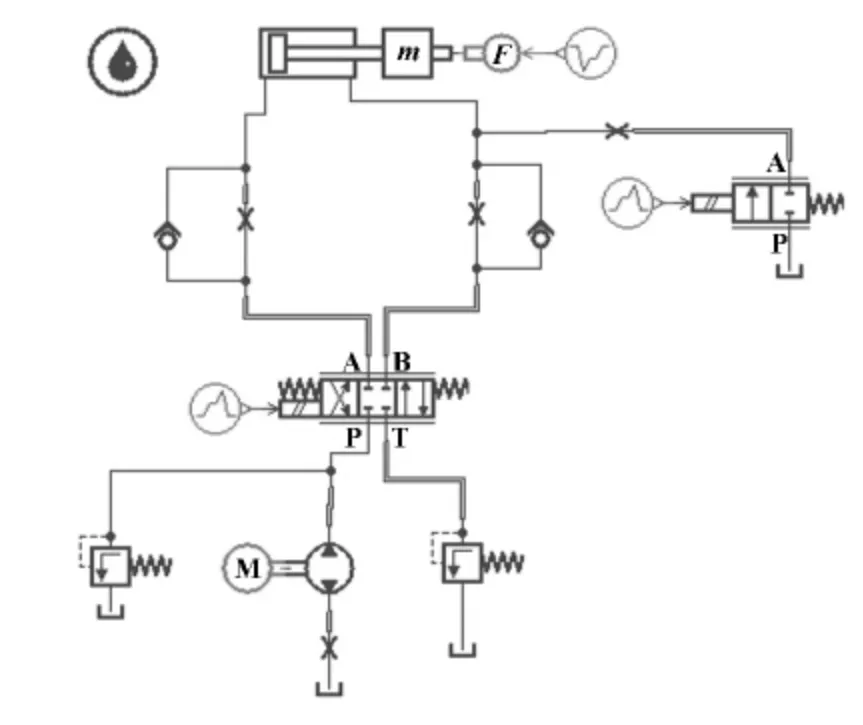
图1 液压系统仿真模型图

仿真过程为:

(1)正常状态下，将液压缸泄漏设置为0;

(2)内泄漏状态下，将液压缸内泄漏设置为5 L/ (min·MPa);

(3)外泄漏状态下，将两位两通换向阀通电，液压缸泄漏设置为0。

得到不同状态下进油腔压力、进出油腔压力差及杆行程的数据如图2—4 所示。仿真时间为10 s。

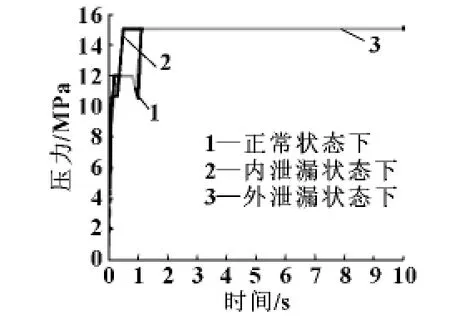
图2 不同状态下进油腔压力曲线

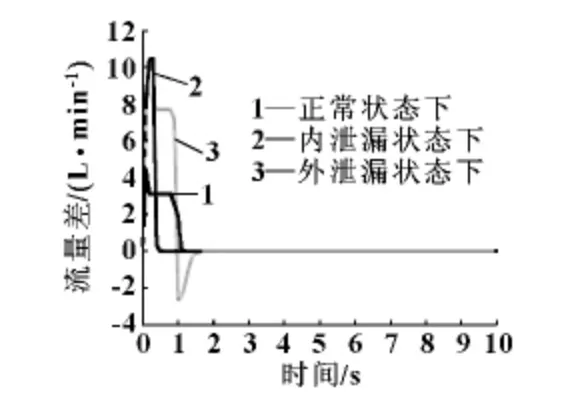
图3 不同状态下进出油腔流量差曲线

图4 不同状态下杆行程曲线

对上述仿真结果进行处理，对其进行特征提取，现将液压缸内泄漏设置为3 L/ (min·MPa)，得到其进油腔压力曲线、进出油腔流量差曲线和杆行程曲线，如图5—7 所示。

图5 3 L/(min·MPa)内泄漏状态下进油腔压力曲线

将测试信号曲线进行特征提取后数据代入到公式中，得到该状态下的隶属度，进而得到各类传感器对不同故障类型的信度函数，最终利用D-S 数据融合方法得到传感器组对各类故障的一致性描述，进而完成对故障类型的判别。信度函数分配见表1。

图6 3 L/(min·MPa)内泄漏状态下进出油腔流量差曲线

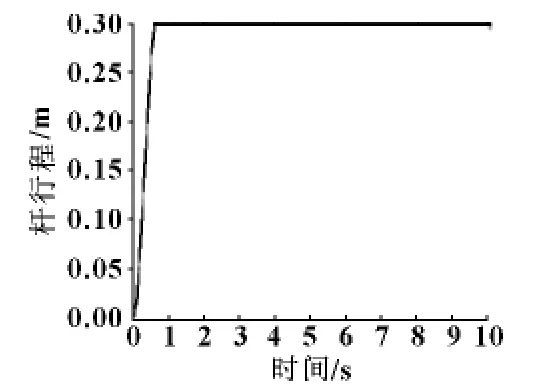
图7 3 L/(min·MPa)内泄漏状态下杆行程曲线

表1 信度函数分配

4 结论

将D-S 理论引入到液压缸泄漏故障诊断领域，仿真结果说明:这种方法可实现非介入式泄漏故障诊断，可避免液压缸的拆解及单传感器的低精度问题，为液压缸泄漏故障诊断提供了一项新的检测技术。

【1】陆望龙.液压系统使用与维修手册［M］.北京:化学工业出版社，2008:308 －330.

【2】黄志坚，袁周.液压设备故障诊断与监测实用技术［M］.北京:机械工业出版社，2005.

【3】何友，王国宏.多传感器信息融合及应用［M］.北京:电子工业出版社，2000.

【4】蔡伟，李敏，张志利.液压系统监测诊断中的传感器优化配置技术［J］.液压与气动，2012(5):75 －78.

【5】李振中，孙玉清，陈海泉，等.基于多传感器数据融合的液压泵故障诊断研究［J］.机床与液压，2006(8):214 －215.