管—土滑动接触海底管道振动波数的解析求解

严 谨，刘敬喜，张 娟

（1广东海洋大学 工程学院，广东 湛江524088；2华中科技大学 船舶与海洋工程学院，湖北 武汉430074）

1 引 言

海底管道是海上油气田的生命线，在海上能源开采中发挥着重要作用。但因其工作条件恶劣，常会发生因腐蚀、波流冲刷、机械破坏等原因而产生的各种损伤和缺陷，导致管内流体泄漏，不仅会造成资源的极大浪费，而且还会造成严重的安全事故以及环境污染。

利用声信号的相关分析方法检测海底载流管道的泄漏，在工程上有现实意义。互相关分析法的基本原理就是利用沿管道布置的两个加速度传感器测量泄漏噪声信号，传感器放置在阀门顶端，通过噪声信号到达两个传感器的时间差对两端声波信号进行相关分析，从而确定泄漏点[1]。但是对于海底管道，由于声信号的传播速度会受到管道周围土壤的影响，给准确定位漏损点带来一定的误差。在理论上，探讨海底载流管道的振动波数传播特性，对解决这一问题具有重要的指导意义。

海底载流管道振动是典型的土—管—液三相耦合问题，对这一复杂问题的研究目前尚无成熟的理论。Muggleton等人[2-3]提出了一种用以预测埋地充液管道波数和波衰减的低频理论模型，并进行了实验验证。但该模型将管周围土壤视为流体，把土体对管壁的作用作为一种压力项来处理，没有考虑管-土的剪切效应，这和实际情况有一定差距。刘敬喜[4-5]将土壤作为弹性介质考虑，采用波传播的方法得到耦合系统的特征方程，求取了频散特性以及实固有频率，提出了解决这类问题的很好思路。何勇等人[6]采用等效线性近似的方法，建立了考虑海底悬跨管道的几何非线性特征的悬跨管道疲劳可靠性分析方法。Gao等人[7]则特别针对塑料管道在埋地状态下的声学漏损探测问题进行了探讨。

对于浅埋于土壤中的管道，漏损检测研究主要集中在低频段[1-2]。低于环频率时，充液管道中主要有四种波传播能量[8]：周向波数n=0的三个对称波和n=1梁弯曲波。对于n=0波，第一种s=1是主要的管内流体传播的波；第二种s=2是管内壳体的压缩波；第三种s=0是扭转波且和流体是无耦合的。作者对充液管道轴对称波的传播与衰减特性进行了分析[9]。

本文在文献[2，5，8-9]的基础上，以浅埋于海底的载流管道为对象，将管道与海底泥沙的接触视为滑动接触，推导了周向波数n=0轴对称载流管道振动耦合方程，采用低频近似得到了求解流体波（s=1）和壳体压缩波（s=2）振动波数的简化解析表达式，并通过数值方法计算了这两种典型波的传播和衰减特性，并特别分析了周围土壤对管道声传播的影响。研究结果可为海底载流管道漏损的精确检测提供理论支持。

图1 海底管道坐标示意图Fig.1 The co-ordinate system for a seabed fluid-filled pipe

2 理论模型

2.1 管道振动方程

假定浅埋于海底的管道做周向波数n=0的轴对称振动，其解包含两种类型的波，s=1，2，分别对应于管内流体传播的波（s=1）和壳体的压缩波（s=2），这两种波都参与了土壤、管道和流体的振动。管道的坐标系如图1所示，图中u、v和w分别为壳体的轴向（x）、切向（h）和径向（a）位移。以下采用适用于薄壳的Kennard’s壳体简化方程[10]，由于忽略了壳体的弯曲刚度，因此仅在环频率以下有效。

根据轴向的力平衡原理有

假定没有环向的振动，根据径向的力平衡可得出

其中，σθ、σx分别是管道环向、轴向应力，σrx、σrr分别是外部土作用于管上的轴向和法向应力，ρ是管体材料密度，a和h分别是管壁的半径和厚度（h＜＜a）。

根据Hooke定律有

联合方程（1）、（4）可以得到

联合方程（2）、（3）可以得到

方程（5）、（6）即为管道做周向波数n=0轴对称振动的耦合方程。

假设满足载流管道振动位移的波解形式是

其中，ks表示轴向波数，ω是圆频率。

2.2 管内液体的振动

假设管内流体为无粘、无旋及各向同性，满足Helmholtz波动方程。管内流体压力pf可表示为[11]其径向分量和轴向波数的关系为为流体自由波波数，J0（）是零阶第一类贝塞尔函数。

2.3 周围土壤动力方程

简化分析起见，将管道周围土体视为均匀线弹性体，则介质中任意点的位移U（x,θ,r,t）满足弹性动力方程[12]

其中，λm，μm是拉梅常数，ρm是土介质密度，▽是哈密顿微分算子，△表示膨胀量，在柱坐标中表示为

其中，ur、uθ和ux分别表示柱坐标中r，θ和x方向相应位移，用其表示的三个正交方向旋转分量如下：

根据虎克定律，应力应变之间有如下关系

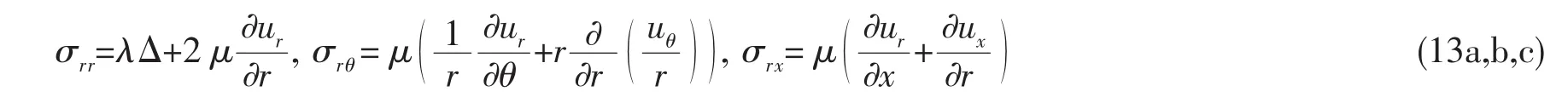
假设土的位移级数可表示为

对于轴对称振动，结合以上方程，可以得出如下两个关系式

方程（18）、（19）分别是零级和一级贝塞尔方程，它们对于圆柱壳向外传播波的解可表示为

其中，G、H为常数，H0（）、H1（）分别是零阶和一阶第二类汉克函数。

为了满足方程（18）-（21），位移Um和Wm需具有如下形式[13]：

其中，A、C是常数。

根据方程（13），（22）和（23），计算周围土应力：

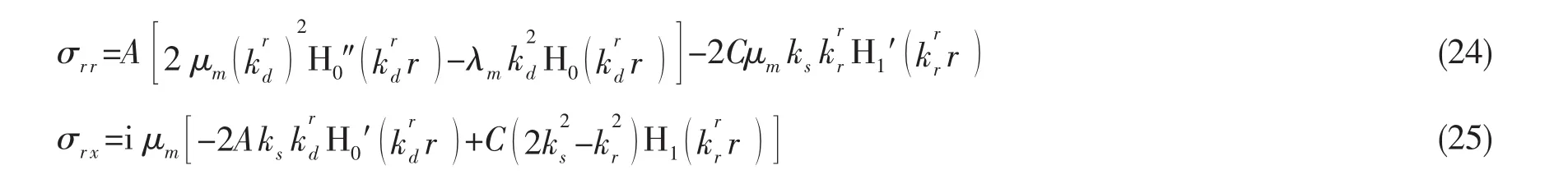
其中，Hn′（）=∂Hn（）/∂r，Hn″（）=∂2Hn（）/∂r2。

2.4 耦合振动方程

对于浅埋于海底的管道，管道和周围沙土的结合力较弱，管—土之间的耦合可以近似地看作滑动接触。这样，在界面r=a处，切向应力σrx=0，因此由方程（25）可得

在管—土接触面，考虑滑动接触状况，位移满足边界条件

同理，在管内流体与管壁的接触面上，流体径向位移也必须等于结构的径向位移。由动量方程得到

联合方程（9），（27）和（28）得到

将方程（23），（24），（27）和（29）代入到（5），（6）中得到：

联合方程（26）和（30），消除常数A、C得到

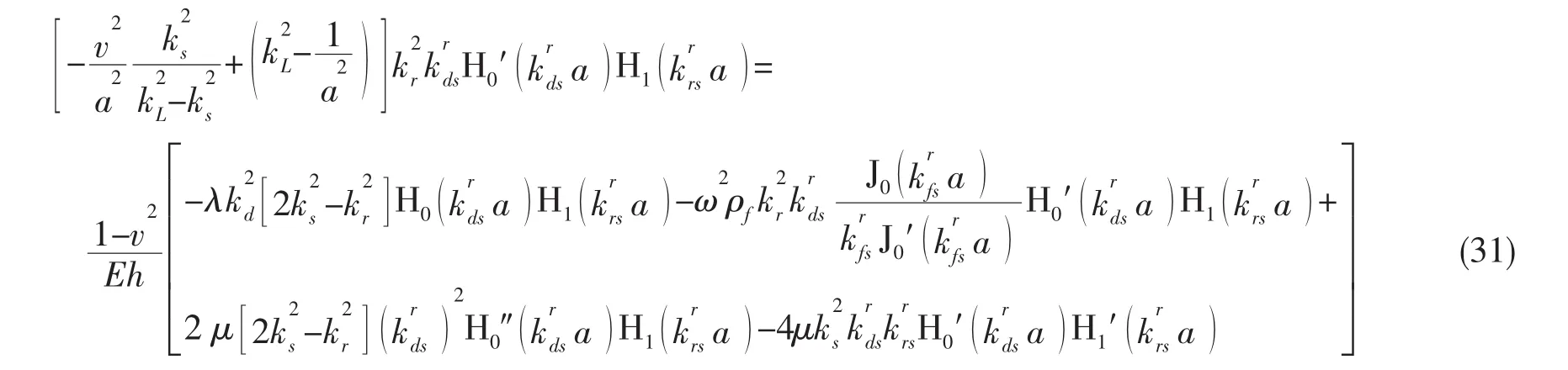
即为此耦合系统的振动波数方程。

3 低频近似求解

由于漏损管道的声能量传播主要集中在低频段[1]，因此以下主要对低频下的波数方程进行深入研究，试图给出相对简化的波数解表达式以及探讨相关的物理解释。

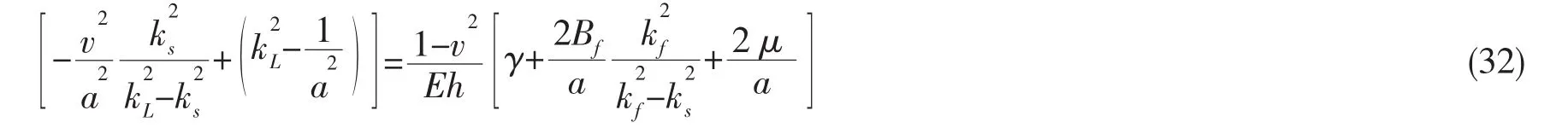
其中，Bf是内部流体的体积模量，为耦合项。

对于充液管道的轴对称振动，主要有两种形式的波解，s=1，2，分别对应流体波和壳体压缩波，这两种波都参与了土—管—液的耦合振动。

3.1 s=1流体波

对于s=1流体波，一般认为k1远大于平面压缩波波数kL，即s=1波的波速比平面压缩波波速慢很多。在方程（32）中令可得

从波数k1的简化表达式（33）中，很容易辩识到：（2Bf/a）是管内流体的刚度项，（Eh/a2）是管壁的刚度项，（ρhω2）是管壁的质量项，（2 μm/a）是土的剪切刚度项，γ是耦合项。这对于从物理概念上理解影响波数的因素提供了帮助。

在极低的频率下，耦合项γ趋于零，因此方程（33）变为

这一结果和文献[14]结论相吻合。

对于管道周围无介质情况，上式进一步简化为

这一结果与Pinnington和Briscoe[8]对于真空中充液壳的结论吻合。

比较方程（33）-（35）可以看出，当充液管道外存在土介质时，土的剪切刚度（2 μm/a）会对波数带来较大影响，基本与波数成反比变化。

3.2 s=2壳体压缩波

根据以上公式进行了数值计算。波为壳体压缩波，根据一般常识，它比流体的波数要小，令得

在极低的频率下，耦合项γ趋于零，上式变为

对于管道周围无介质情况，上式进一步简化为

同样，这一结果与Pinnington和Briscoe[8]对于真空中充液壳的结论相吻合。

4 数值分析

以海底载流管道为例，根据以上公式进行了数值计算。流体为水，管道材料为钢，弹性模量为E=1.92×1011N/m2，泊松比 ν=0.3，质量密度 ρs=7 800 kg/m3，ρf=1 000 kg/m3，管道厚径比h/R=0.05，cL=5 200 m/s，cf=5 200 m/s。土壤的质量密度为 ρm=2 000 kg/m3，c1=1 500 m/s，c2=300 m/s。由于壳体材料本身具有耗散，所以在计算中，需将弹性模量E替换成E（1+iη）以考虑波传播中的材料损耗，其中η是材料损耗因子，这里取η=0.02。本文利用牛顿迭代法在整个复平面上求解，最后得到复量形式的波数解，解的实数部分表示波的传播速度，解的虚数部分表示波的衰减。

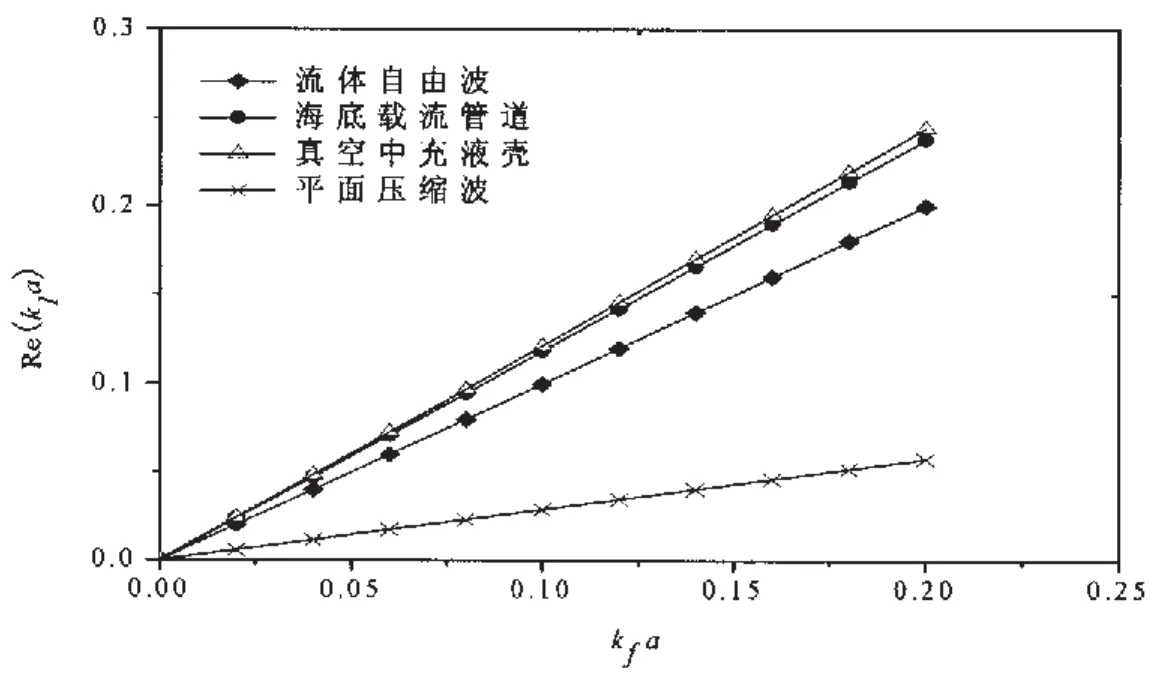
图2 流体波波数的实部（s=1波）Fig.2 Real part of wavenumber for s=1 wave

4.1 流体波的传播与衰减

图2给出了海底载流管道流体波（s=1波）波数的实部随频率变化的情况。为了比较研究管道外部弹性介质的影响，同时给出了真空中充液管道的结果作参考。由图可见，在相对低的频域内，s=1波的波数基本随频率呈线性增加，波数值明显大于平面压缩波，根据波数和波速的关系（k=ω/c），可知管内流体波比平面压缩波的传播速度慢很多，这也符合以前文献对于s=1流体波传播特性的认识[8-9]。相比于真空中充液管道，海底管道的波数有所降低，这主要是受到周围弹性介质的影响，这一结果也印证了Muggleton等[2]的结论。从以上表达式（33）可以看出，管外弹性土介质主要以刚度项（2 μm/a）形式对波数产生影响，使管壁流体波的波数减少，也即加快管壁流体波的传播速度。

图3进一步给出了低频情况下海底载流管道流体波波数实部的几种近似计算结果。由图可见，通过低频近似公式（33）-（34）计算的结果与完全解非常接近，近似公式（35）的计算结果为真空中充液壳结果。因此，低频情况下采用近似公式预测波的传播特性是可行的。

图4描述了流体波的衰减状况，用波在单位传播距离衰减的分贝数（dB）来描述。传播损失可由波数虚部计算[2]：Loss(dB/per distance)=20Im{ka}/ln(10)。由图可见，传播损失也随频率而变化，在所研究频段，频率越高，衰减量越大。通过低频近似公式（33）-（34）计算的衰减结果与完全解同样比较接近，但其差别大于图3实部之间的差别，这主要是由于低频近似处理时对波数虚部的简化影响较大引起的。相比于真空中充液管道，海底管道的传播损失有所降低，这主要是受到周围弹性介质的限制影响。由于波的传播距离主要取决于衰减特性，对其研究有助于预估某一种波在特定频率下传播的实际距离，对于漏损检测具有重要意义。

图3 流体波波数（s=1波）实部近似公式结果比较Fig.3 Comparison of results of approximate formulas for real part of s=1 wave

图4 流体波的衰减（s=1波）Fig.4 Loss in dB/unit distance for s=1 wave

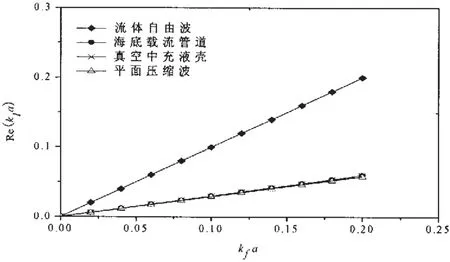
图5 壳体压缩波波数的实部（s=2波）Fig.5 Real part of wavenumber for s=2 wave

4.2 壳体压缩波的传播与衰减

图5给出了壳体压缩波（s=2）波数实部随频率变化的情况。由图可见，壳体压缩波波数远小于流体波波速，也就是说壳体压缩波传播速度远快于流体波传播速度，同时壳体压缩波波速十分接近平面压缩波波速，这一结果也符合以前文献对于s=2壳体压缩波传播特性的认识[2，8]。相比于真空中充液管道，周围土弹性介质对s=2波的影响较小，波数基本未发生改变。这一现象也和文献[2]得到的s=2波在传播中较少受周围环境影响的结论是吻合的。从以上表达式（36）可以看出，管外弹性土介质主要体现以刚度项（2 μm/a）形式对波数产生影响，但是相比于其他项而言，其影响程度较小。

图6进一步给出了低频情况下海底载流管道壳体波波数实部的几种近似计算结果。由图可见，与s=1波相似，通过低频近似公式（36）-（38）计算的结果与完全解非常接近。

图7描述了用分贝数（dB）表示的s=2波单位传播距离衰减状况。可以看出，壳体压缩波的衰减也随频率变化，和波数实部的变化规律相似，较少受到周围介质的影响。同样，低频近似公式计算的衰减结果与完全解也非常接近。

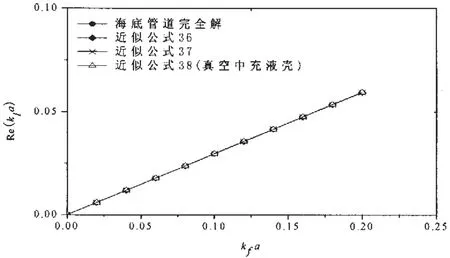
图6 壳体波波数实部近似公式结果比较Fig.6 Comparison of results of approximate formulas for real part of s=2 wave

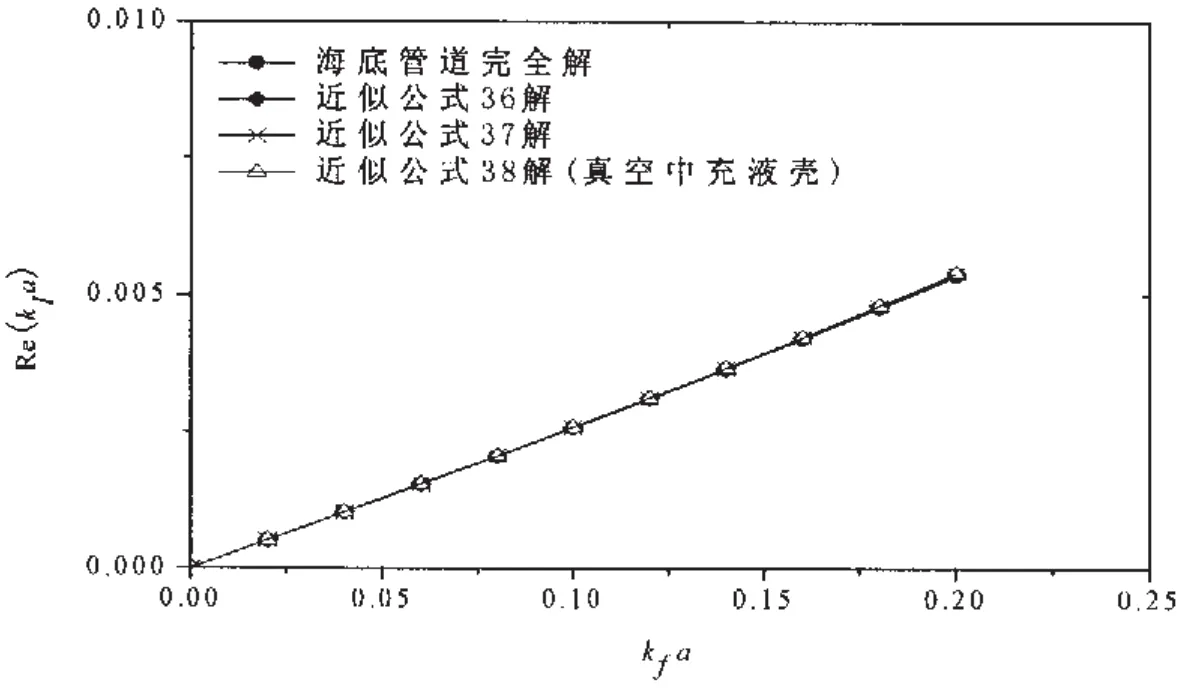
图7 壳体压缩波的衰减（s=2波）Fig.7 Loss in dB/unit distance for s=2 wave

5 结 论

本文对管—土滑动接触海底载流管道轴对称波进行了研究，推导了低频域流体波（s=1）和壳体压缩波（s=2）振动波数的简化解析表达式，利用数值计算分析了波在管道中的传播和衰减特性。可以得到如下结论：在较低的频段内，弹性介质中载流管道的波传播和衰减均随频率呈线性变化，管外土介质主要以刚度项形式影响波数，使流体波（s=1）波数有减少趋势（即可加快波的传播速度），而对壳体压缩波波数（s=2）的影响较小，可以忽略不计。在低频情况下，采用近似公式预测管道波的传播特性是可行的，可以大大减少计算工作量。研究结果可为准确预测声信号在管道中的传播特性提供帮助，以利于提高管道互相关检测法的精度，具有一定的实际应用前景。

需要说明的是，海底载流管道振动涉及土—管—液的三相耦合，是一个复杂的工程实际问题。本文将管道周围的土壤作为均匀线弹性体处理，将土—管之间的耦合视为滑动接触，以及将管道做无限直管考虑等，都是一种近似处理。在实际分析中，还应该考虑实际土壤的本构关系、土壤中饱和水及土壤粘性等的影响，管—土接触要全面考虑实际情况，这些都需要今后进一步地完善理论模型。

[1]Hunaidi O,Chu W T.Acoustical characteristics of leak signals in water distribution pipes[J].Applied Acoustics,1999,58:235-254.

[2]Muggleton J M,Brennan M J,Pinnington R J.Wavenumber prediction of waves in buried pipes for water leak detection[J].Journal of Sound and Vibration,2002,249(5):939-954.

[3]Muggleton J M,Brennan M J,WLinford P.Axisymmetric wave propagation in fluid-filled pipes:Wavenumber measurements in vacuo and buried pipes[J].Journal of Sound and Vibration,2004,270(1-2):171-90.

[4]刘敬喜,李天匀,刘土光.基于波传播方法的埋地管道的振动特性分析[J].固体力学学报,2005,26(2):187-192.

[5]刘敬喜,李天匀,朱翔等.海底载流管道轴对称波频散特性析[J].海洋工程,2007,25(2):98-103.

[6]何 勇,龚顺风,金伟良.考虑几何非线性的海底悬跨管道疲劳可靠性分析方法[J].振动工程学报,2009,23(2):313-318.

[7]Gao Y,Brennan M J,Joseph P F.On the effects of reflections on time delay estimation for leak detection in buried plastic water pipes[J].Journal of Sound and Vibration,2009,325:649-663.

[8]Pinnington R J,Briscoe A R.Externally applied sensor for axisymmetric waves in a fluid-filled pipe[J].Journal of Sound and Vibration,1994,173:503-516.

[9]Yan J,Zhang S L,Zhang J.Propagation and attenuation of axisymmetrical wave in fluid-filled pipes[J].Journal of Ship Mechanics,2011,15(6):688-697.

[10]Leissa A W.Vibrations of shells[M].Washington,D.C.:Scientific and Technical Information Office,NASA,1973.

[11]Morse P M,Ingard K U.Theoretical acoustics[M].New York:McGraw-Hill,1968.

[12]杨桂通,张善元.弹性动力学[M].北京:中国铁道出版社,1988.

[13]Kolsky H.Stresses waves in solids[M].New York:Dover Publications,INC,1952.

[14]White J E.Underground sound:Application of seismic waves[M].New York:Elsevier Science Ltd,1983.

附录 汉克函数近似表达

对于小变量情况，适用以下近似表达：