喷水推进器进水流道空化和流动分离的模拟控制研究

康希宗，王绍增

(中国人民解放军91208 部队，山东 青岛266102)

0 引言

船舶喷水推进器主要由喷水推进泵、进水流道、喷口和转向倒车机构等部件组成。进水流道是喷水推进器的一个重要部件，其功能除了输送水流外还将船底来流的能量传递给装在尾板上的喷水推进泵。在进水流道里，来流能量的利用率直接影响着整个喷水推进器的效率［1］。对于几何结构一定的进水流道，弄清何时发生空化、何时发生流动分离将对我们充分利用来流的能量从而提高推进效率起着至关重要的作用。本文针对国外某型进水流道，运用计算流体力学方法，通过大量数值实验模拟了不同进速比和不同航速情况下的流动性能，绘制了该型流道正常工作的工况性能图谱，得到了空化区、流动分离区与正常工作区的分界线，这对避免流道产生空化和流动分离具有重要的参考价值。

1 数值模拟的建立

1.1 初始条件的确定

当舰船以某一航速稳定航行时，喷水推进器进水流道内的流场分布是确定的，通过计算流体力学的方法可以把该流场的分布情况精确模拟出来。但数值模拟时只知道进口速度而不知道出口速度是无法求解的，所以首先要确定流道出口的速度分布。由于流道出口速度分布较为复杂且不容易用数学表达式描述，因此本文选用流量代替出口的速度分布作为已知条件来进行数值模拟，即数值模拟的初始条件选用航速和流道出口处的流量。

1.2 进速比IVR

进速比IVR 的定义为进水流道出口速度的平均值与航速的比值，它与流量之间的联系如公式(1)所示。在航速一定的条件下，由于进速比IVR 与流量成正比，因此可以用对进速比IVR 的控制实现对流道出口流量的控制，以实现不同工况时的数值模拟。

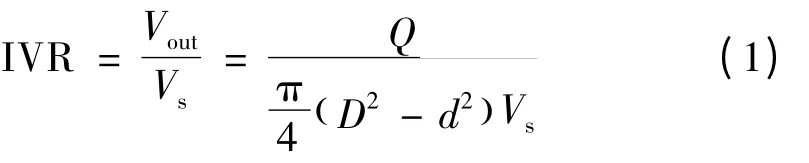
式中:Vout表示流道出口处的平均速度;Vs表示船的航速;Q 表示流量;D 表示流道出口直径;d 表示叶轮轴直径。

1.3 流动性能的评价

航速和进速比确定之后，进水流道的流场分布就确定了。为了研究空化和流动分离两种现象的发生、发展和消失的过程，本文在对流场分布进行分析时，主要考察空化和流动分离两个性能指标，最后补充考察了流道出口的不均匀性，以确定最佳工况点。

空化是指液体内局部压力降低时，液体内部或液固交界面上蒸汽或气体的空穴 (空泡)的形成、发展和溃灭的过程。空化会引起喷水推进器流动损失增加，推力下降，振动和噪声加剧等一系列负面影响。

流动分离又称为边界层分离，是指原来紧贴壁面流动的边界层脱离壁面的现象［2］。设计不佳的进水流道内会产生严重的流动分离，使流动损失增大，效率降低，严重影响流动性能。

流道出口的出流速度分布越不均匀，就越容易增加喷水推进泵的周期性脉动。这不仅会造成泵的耗功增大，效率下降，而且会引起振动加剧，噪声增强，抗空化性能下降。流道出口流场流动不均匀度ξ 的定义式［3］为

式中:Q 为流道出口的流量;Vx为出口的轴向速度;为出口的平均轴向速度。不均匀度ξ 越小，表示流道出流越均匀，流动性能越好。

2 数值模拟的计算

2.1 几何建模与网格划分

本文的模型选取了MJP 公司的叶轮直径为750 mm的某型进水流道(见图1)。计算域按文献［4］推荐取长、宽、深分别为30D，10D，8D。为保证计算精度，网格划分采用六面体结构化网格，近壁面采用O型网格并进行了加密，网格数为94 万，y +控制在200以内。在流动变化剧烈区域，如唇部、弯管和流道与船底相交处进行了网格加密，第一层网格距壁面0.1 mm (见图2)。

图1 流道计算域的几何建模

图2 网格划分

2.2 控制方程与数值求解

进水流道的流场是复杂的粘性不可压湍流流动，它的速度、动量等都是低尺度、高频的波动量［5］。本文采用目前工程上应用最为成熟和广泛的雷诺时均方法进行数值计算，把湍流运动看作时间平均流动和瞬时脉动流动的叠加［6］。将基本的N-S 方程引入Boussinesq 假设得到的流动控制方程组为

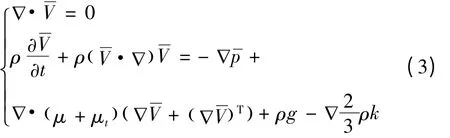
计算域上游设为速度进口，速度大小及梯度分布受航速及边界层的影响。根据R. Svenssen 和L. Grossi对喷水推进船实船的测量结果［7］，边界层厚度δ 可采用Wieghardt 公式近似求取δ =0.27x (Re)－1/6，其中x 为距船首的距离，Re 为雷诺数。速度分布采用平板边界层速度分布表示［8］为

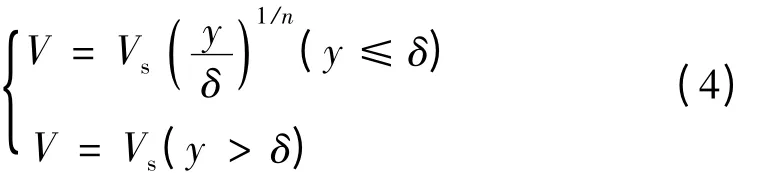
式中:V 为边界层内流速;δ 为船底边界层厚度;y 为距船底的距离;指数n 取为9。流道出口设为流量出口，进水流道及船体设为无滑移壁面。

3 计算结果及分析

3.1 进速比IVR 对流动性能的影响

表1 为MJP750 流道在额定航速为36 节、不同IVR时流动性能的计算结果。由表1 可得，在航速为36 节时，此型流道的正常工作范围对应的IVR 为(0.62，0.78)，即流量应大于5073 kg/s，小于6382 kg/s。当IVR 大于0.78 时，流体的动能较大，在弯头转弯处形成低压区，压力低于汽化压力发生空化，此位置接近泵的进口，会对泵的进流产生严重影响，甚至会引起泵体的振动，大大降低喷水推进器的效率，在工作中应当严格避免此类工况的发生。当IVR 小于0.62 时，由于流体动能较小，动能不足以使流体到达弯头的顶部，因此背部产生流动分离;同时随着流量的降低，唇部下方的速度越来越大，产生低压区从而产生空化，此时的空化不会进入流道内部，因此对整个流动性能的影响不大。当IVR 介于0.62 和0.78 之间时，不会产生空化和流动分离，且不均匀度随流量的增大而减小。因此在流道设计时，应当把额定工况选在流量为5800 kg/s 左右。由于上述计算没有考虑轴的影响，如果把轴的影响加进去，该流量应该再减小。实际上，该型流道的设计流量为5700 kg/s，这也说明了流道设计时应当充分考虑流量的影响，即进速比IVR 的影响。

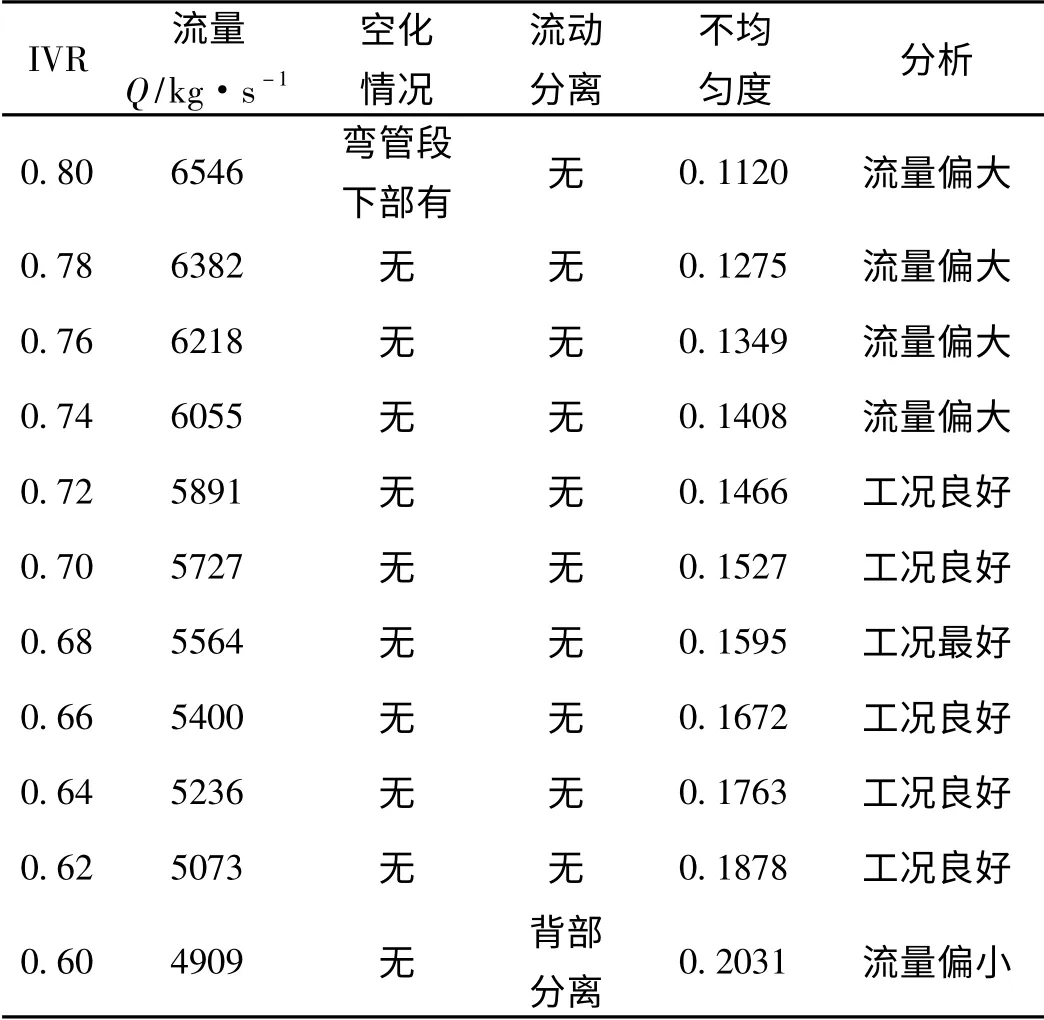
表1 36 节不同IVR 时流动性能比较

以上的计算结果还说明，对于几何形状一定的进水流道，在某一航速下，有一个正常工作范围，对应于IVR 或流量的一个取值范围，如果我们把各个航速下的正常工作的IVR 或流量范围求出，即可得到该型流道的工况性能图谱。为此，我们需要研究航速对流动性能的影响。

3.2 航速对流动性能的影响

为分析不同航速下进水流道流动性能的变化，在36 节额定航速的基础上又增加了五个不同的航速(9节、18 节、27 节、45 节、54 节)的数值模拟，涵盖了当今船舶常用航速范围。各航速下的数值计算结果分别列表2 ～6。

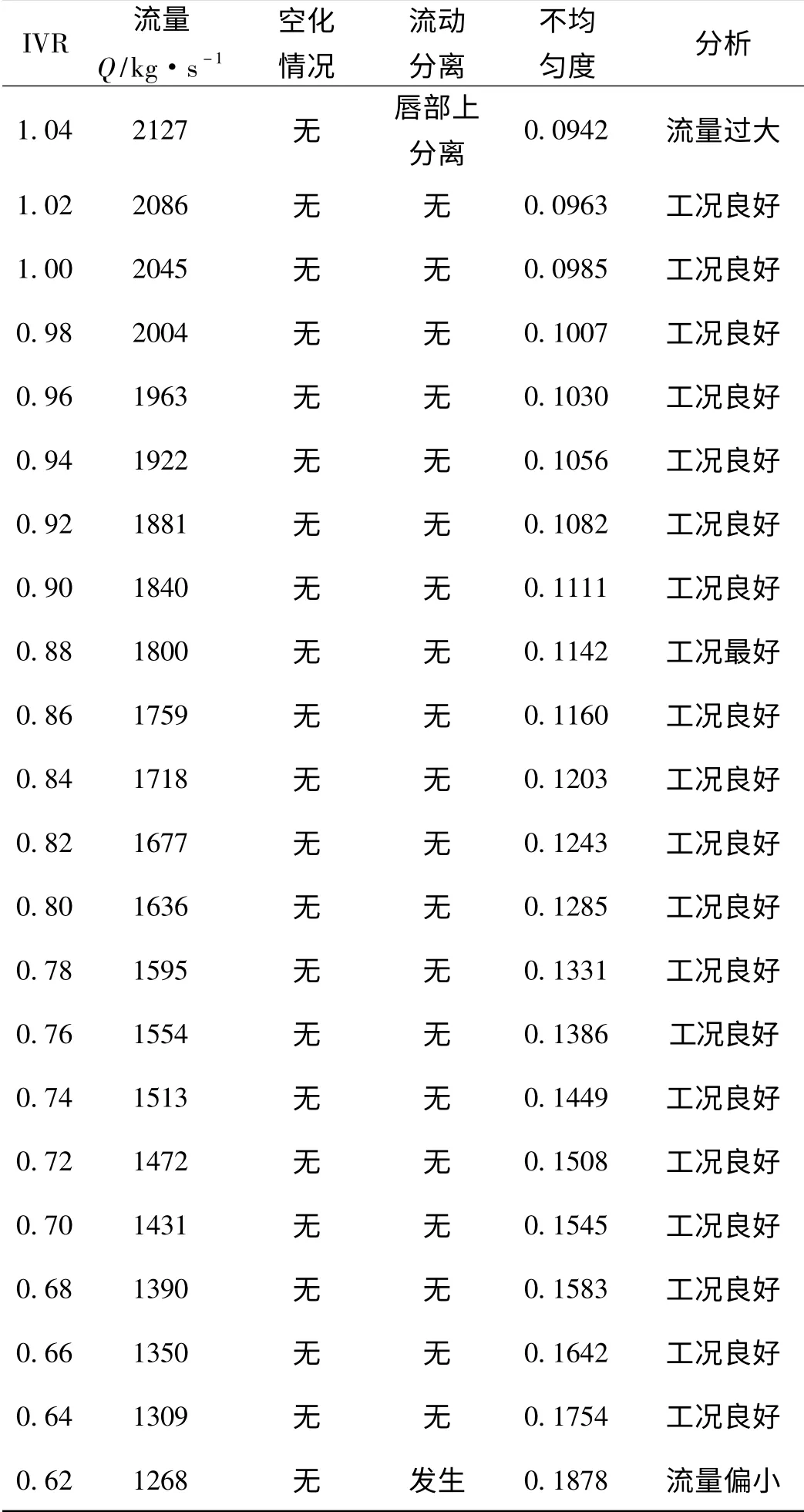
表2 9 节不同IVR 时流动性能比较

表3 18 节不同IVR 时流动性能比较

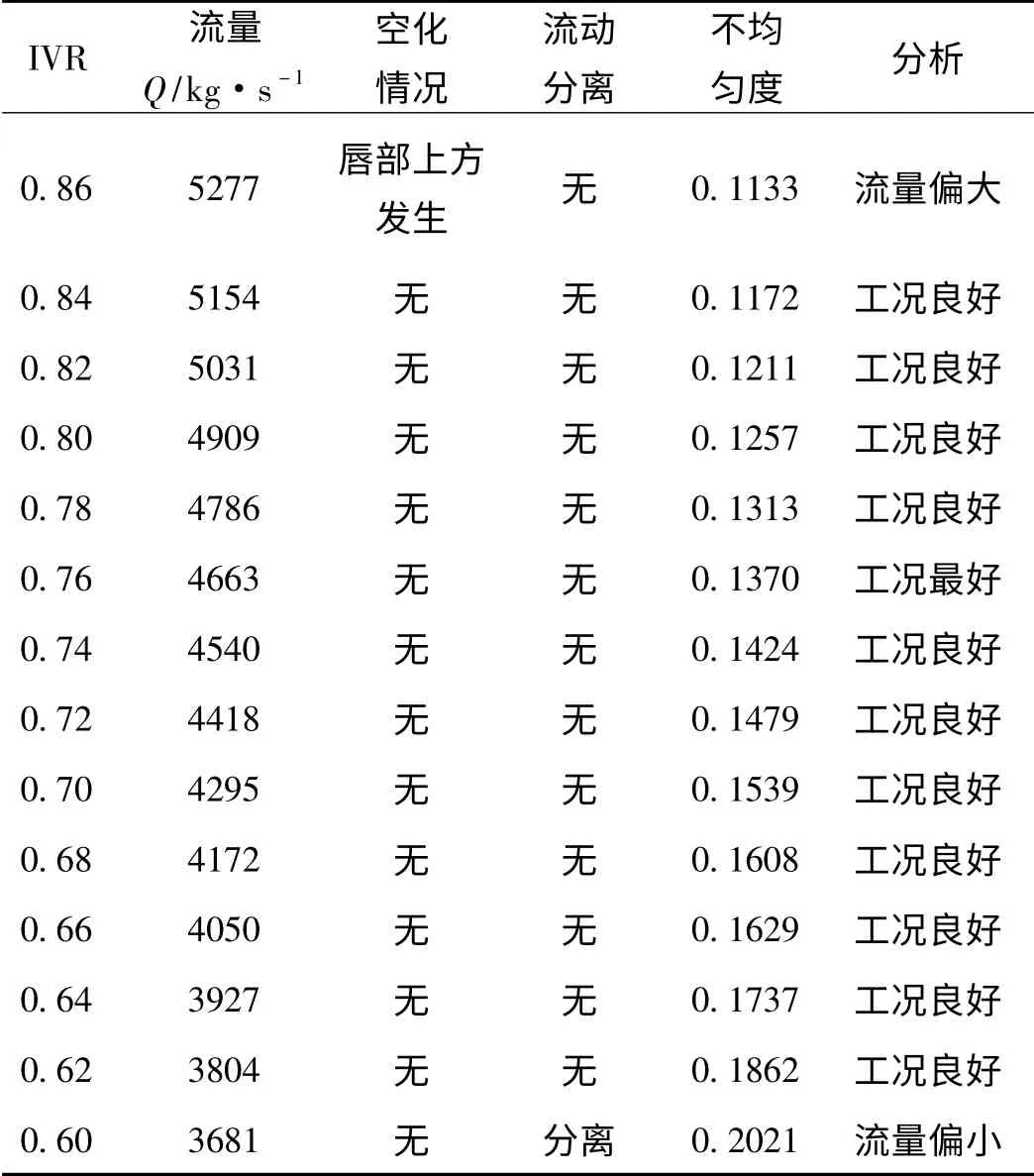
表4 27 节不同IVR 时流动性能比较

表5 45 节不同IVR 时流动性能比较

表6 54 节不同IVR 时流动性能比较

以上计算结果表明，该型流道在9 节时最佳工作范围为IVR 取(0.62，1.02)，在此范围内流道均不会发生空化和流动分离，且不均匀度随IVR 的增大而减小。若以尽量远离空化和流动分离发生工况且不均匀度尽量小为最佳流动性能的判断原则，可以得到该航速下一个最佳IVR 的值，即9 节时最佳IVR 为0.88。同理，18 节、27 节、36 节、45 节、54 节时正常工作的IVR 范围分别为(0.62，0.92)， (0.62，0.84)，(0.62，0.78)，(0.62，0.72)，(0.62，0.66)，最佳IVR 分别0.84，0.76，0.68，0.66，0.64。将上述结果作图得到图3。

图3 IVR 与航速的关系

从图3 中可以看出:随着航速的增加，能正常工作的最小IVR 一直保持不变，均在0.62;最大IVR 逐渐减小，因此正常工作范围也逐渐减小，当增大到54节时，正常工作范围已经变得相当狭窄，这对流道流动性能是相当不利的。最佳IVR 随航速的逐渐增大而不断减小，因此高航速时把IVR 控制在合理范围内是决定流道设计好坏的关键一环。同理，分析各个IVR所对应的流量随航速的变化关系可以得到图4。

图4 流量与航速的关系

从图4 中可以看出:正常工作时的流量随航速的增大而增大，每个航速所对应的流量范围均比较狭窄，约为1000 kg/s，因此流量对流道流动性能的影响作用很大，要想设计出各个工况下性能均优的流道，就要严格控制各个航速下通过流道的流量。

综合以上结果可得:

1)对于几何结构一定的一型进水流道，其工况性能图谱可以分成三个区:空化区，在最大IVR 线(或最大流量线)以上，流道在本区内工作时会产生空化;正常工作区，在最大和最小IVR 线(或最大和最小流量线)之间，流道在本区工作时工况正常;分离区，在最小IVR 线(或最小流量线)以下，流道在本区工作时产生分离。

2)由于IVR 随航速的变化关系曲线近似直线，因此可以用某一高航速(如54 节)和某一低航速(如9节)的值来估计整个正常工作区的范围。

4 小结

本文对某型进水流道在不同进速比IVR (流量)、不同航速的情况下进行了数值模拟，分析了进速比IVR(流量)、航速对进水流道流动性能的影响，得出以下结论:

1)对于几何结构一定的进水流道，其正常工作范围受航速和IVR (流量)共同影响。当航速一定时，只有IVR (流量)在某一特定范围流道才能正常工作。

2)根据不同航速下正常工作的IVR (流量)，可以作出该型流道正常工作的工况性能图谱，得到空化区、流动分离区与正常工作区的分界线，这对控制进水流道的工作状态十分有利。

3)根据IVR 随航速的变化曲线，可以用两个航速预估流道的整个正常工作范围。

4)正确运用流道工况性能图谱可以方便地控制流道始终处于正常工作状态:低航速对应较小流量，高航速对应较大流量;航速一定时，产生空化后需减小流量，产生流动分离后需增大流量。

［1］Allison J L. Marine waterjet propulsion ［J］. SNAME Transactions，1993，101 :275 －335.

［2］丁祖荣. 流体力学(中册) ［M］. 北京:高等教育出版社，2003:136 －139.

［3］Norbert Willem Herman Bulten. Numerical analysis of a waterjet propulsion system ［D］. Eindhoven:Eindhoven University，2006.

［4］刘承江，王永生，张志宏. 喷水推进器数值模拟所需流场控制体的研究［J］. 水动力学研究与进展，2008，23 (5):592 －595.

［5］汤苏林，毛筱菲. 喷水推进器进水管内流场模拟［J］. 武汉理工大学学报(交通科学与工程版)，2004，28 (6):851 －854.

［6］常书平，王永生，庞之洋，等. 喷水推进器进水流道内流场数值模拟与分析［J］. 武汉理工大学学报(交通科学与工程版)，2010，34 (1):47 －51.

［7］Svensson R，Grossi L. Trial result including wake measurements from the world’s largest waterjet installation［C］ // Proceedings of international conference on waterjet propulsion II. Amsterdam:RINA，1998.

［8］张拯，王立祥. 关于喷水推进装置平进口边界层影响系数估算的探讨［J］. 船舶，2008 (3):10 －14.