梁式结构损伤诊断应变模态理论研究与仿真分析

张翌娜，刘美菊

（黄河水利职业技术学院，河南 开封 475004）

0 引言

结构功能的破坏往往是从裂缝开始的，一旦结构产生裂缝，其承载能力就会大大降低，致使无法满足其设计功能要求。 因此，工程上也将裂缝视为结构产生破坏的标志。 一些学者对工程结构的损伤诊断理论和方法进行了广泛而深入的探讨。 如侯立群[1]针对大型桥梁结构健康监测中所涉及的几项关键技术问题进行了系统研究；李文雄等[2]通过对遗传算法的特点进行分析，提出以逐步评定并排除无损单元的思路来处理结构损伤诊断问题，并提出了一种3 阶段结构损伤诊断方法；张翌娜[3]探讨了用曲率模态和神经网络对混凝土结构裂缝进行损伤识别和定位的方法。

模态识别是结构测试的重要手段之一。 根据所测物理量的不同，它分为位移模态和应变模态。 位移模态是通过测试位移量，得到模态参数，然后通过这些量对结构的振动物性进行分析。 它已经有了一个比较成熟的体系，但在有些方面（如结构损伤识别），其作用不是很明显。 应变模态是通过测试结构在激励作用下应变的变化来进行模态识别。 本文基于应变模态理论，以一混凝土悬臂梁为研究对象，通过建立不同损伤位置和不同损伤程度的模拟工况，进行结构损伤辨识研究，旨在通过结构损伤前后的位移模态振型与应变模态振型的比较，揭示应变模态在结构损伤诊断中的可行性，为大型工程结构的损伤诊断提供技术支持。

1 应变模态的基本理论

1.1 梁的振动微分方程

应变模态是位移模态的一阶导数，对应于每一个位移模态，必定有一个应变模态与之相对应，二者是同一能量平衡状态的两种不同的表现形式。 以考虑黏滞阻尼和塑性变形条件的横向弯曲振动连续梁为例，其振动微分方程可表示如下：

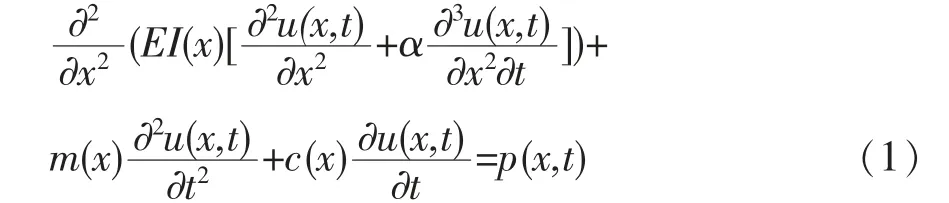
式中：u(x,t)为连续梁中心轴线上任一截面x 在t 时刻的横向振动位移；EI(x)为连续梁的抗弯刚度；m(x)为连续梁单位长度的质量；α 为刚度比例系数。

1.2 模态分析求解方程

要得到上述振动微分方程的解，首先需要了解模态分析的实质。 简而言之，模态分析就是一种坐标变换，其目的在于把原来在物理坐标系统中描述的响应向量转换到“模态坐标系统”中来描述。 该坐标系统中的每一个基向量对应于振动系统中的每一个特征向量，利用每个特征向量之间的相互正交特性，可使待描述的振动响应向量的各个坐标之间相互独立，即在此坐标系统中，上述的振动微分方程可以表示为一个相互无耦合的方程组，每一个坐标均可以单独求解。

因此，根据模态实质与振动理论，如果振动连续梁的各阶位移模态已知，则式（1）的解可以用各阶模态相互叠加的形式表示：

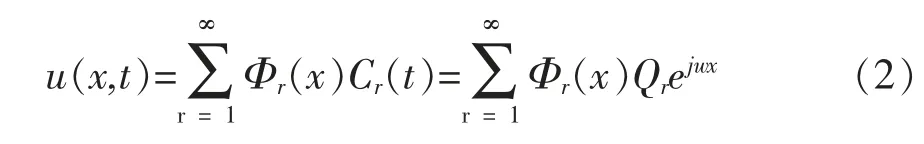
式中：Qr为复数变量；Φr（x）为梁的各阶位移模态；Cr（x）为与位移模态相对应的模态坐标；r 为模态阶数，与结构本身的自由度有关。

1.3 梁弯曲振动的曲率函数

弹性梁在任意截面z 处的弯曲振动的曲率变化函数可用下式表示：

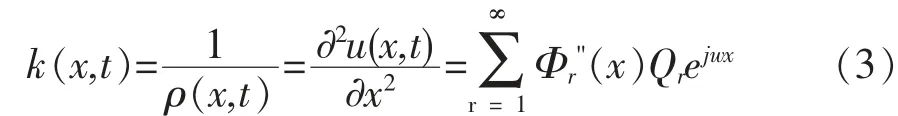
式中： k（x,t）为振动梁的曲率；ρ（x,t）为振动梁的曲率半径。

由材料力学知识可知， 直梁弯曲静力关系如下：

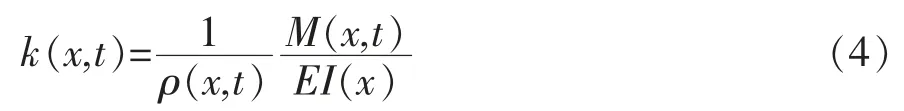
式中： EI（x）为截面抗弯刚度； M（x,t）为截面动弯矩。

1.4 曲率、应变模态方程

如果已知结构各点的位移模态，则结构各点曲率模态的中央差分[3]表达式如下：

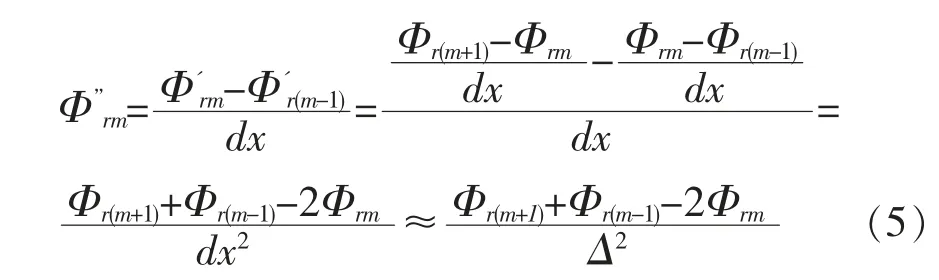
联合式（4）和式（5）可得：

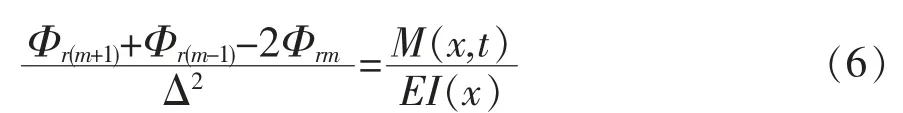
式中：Φ＇rm为第r 阶应变模态函数；Φrm为r 阶位移振动幅值；m 为计算点个数；Δ 为相临计算点的间距。

因此，与位移模态相对应的应变模态可以表示为：

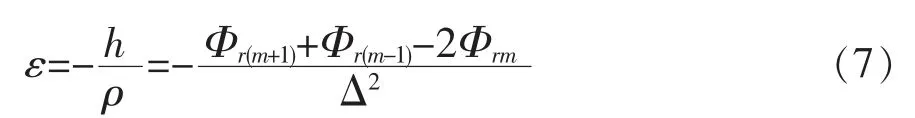
式中：h 为梁上任一截面处测点距中性层的距离。

该式表明了梁的曲率模态、应变模态和位移模态之间的相互关系。

2 悬臂梁损伤诊断仿真分析

以一混凝土悬臂梁为研究对象， 借助ANSYS有限元软件，建立悬臂梁仿真模型。 通过建立不同损伤位置和不同损伤程度的模拟工况，进行结构损伤辨识研究。

2.1 悬臂梁损伤工况

悬臂梁结构尺寸及力学参数如表1 所示，其模型如图1 所示。

表1 悬臂梁结构尺寸及力学参数Table 1 Cantilever beam structure size and mechanical parameters

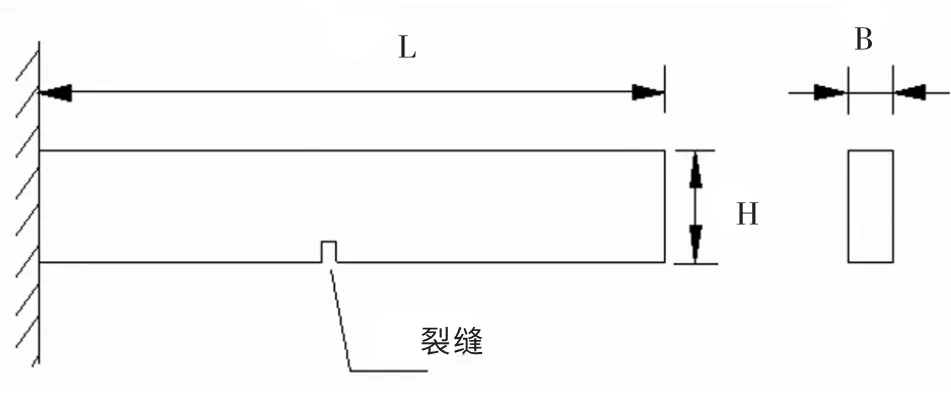
图1 悬臂梁模型结构图Fig.1 Cantilever beam model structure

假定该悬臂梁损伤的缺口宽度为5 mm，5 处损伤位置与固定端距离分别为：100 mm、200 mm、300 mm、400 mm、100&400 mm， 各处损伤深度分别为：10 mm、20 mm、30mm，共计14 个工况（如表2 所示）。

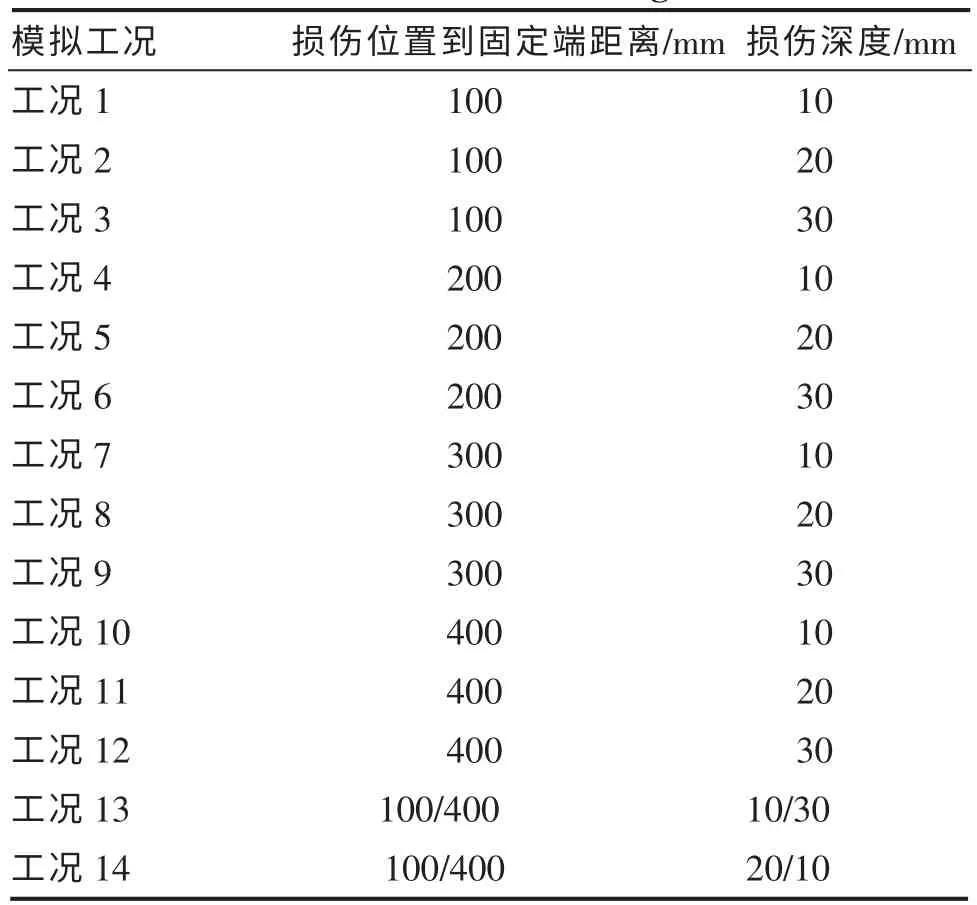
表2 悬臂梁损伤工况Table 2 Cantilever beam damage condition

2.2 悬臂梁损伤对固有模态频率的影响

通过有限元计算，悬臂梁结构无损伤时的前五阶固有频率如表3 所示。

表3 无损伤梁前五阶固有频率Table 3 Natural frequency of zero damaged beam of first five steps

将无损伤悬臂梁和各种工况下的有损伤悬臂梁的频率变化率做对比分析，并对不同损伤位置处的损伤程度加密处理（其中，损伤程度用材料弹性模量的降低来模拟）。 当悬臂梁结构在距固定端200mm 和300mm 处存在损伤时， 频率相对变化率[3～4]如图2 和图3 所示。对比研究结构在同一位置不同损伤程度，可以得出以下结论：（1）随着损伤程度的加剧，各阶结构固有频率都呈下降趋势；（2）随着损伤程度的加剧，结构频率相对变化率都呈非线性增加趋势；（3） 各阶频率相对变化率对损伤的敏感性都不相同[5～7]。

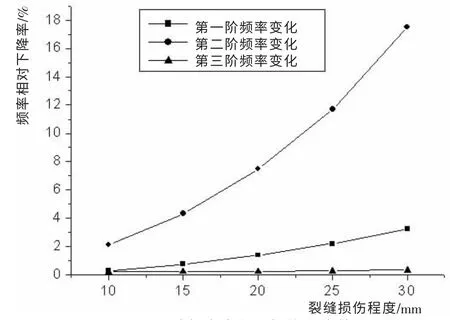
图2 200mm处频率变化与损伤深度的关系Fig.2 Relations of frequency changes and the damaged depth of 200mm

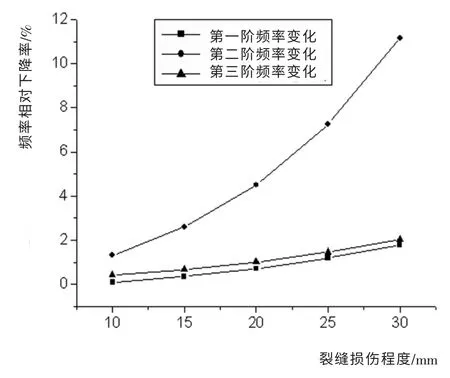
图3 300mm处频率变化率与损伤深度的关系Fig.3 Relations of frequency changes and the damaged depth of 300mm

2.3 悬臂梁的应变模态分析

利用ANSYS 有限元分析软件， 按表2 所示损伤工况，对不同位置、不同损伤程度的悬臂梁进行应变模态分析。 该悬臂梁损伤位置在100mm、200mm、300mm、400mm、100mm&400mm， 损伤程度分别为10mm、20mm、30mm、10mm&30mm、20mm&10mm 时的第一阶应变模态振型如图4～图8 所示。 其中，横坐标为悬臂梁有限元模型单元节点序号，0mm 代表悬臂梁固定端，800mm 代表悬臂梁末端； 纵坐标为关于质量矩阵归一化后的应变模态振型。

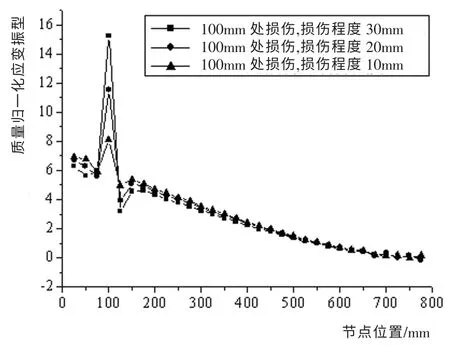
图4 100mm位置损伤处应变振型Fig.4 Strain vibration mode of damaged sites of 100mm

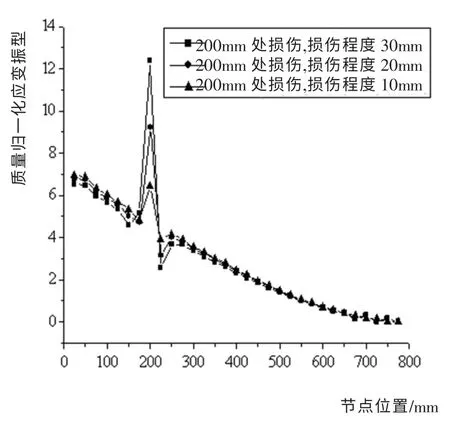
图5 200mm位置损伤处应变振型Fig.5 Strain vibration mode of damaged sites of 200mm

从不同损伤工况下的应变振型图中可以看出，对于悬臂梁构件，无论结构存在的是单处损伤还是多处损伤，结构在损伤位置处的应变振型均有突变发生。 随着损伤程度的加大，损伤位置附近处节点的应变振型也产生了一定波动，亦即大损伤对损伤附近的区域也会产生一定的影响。

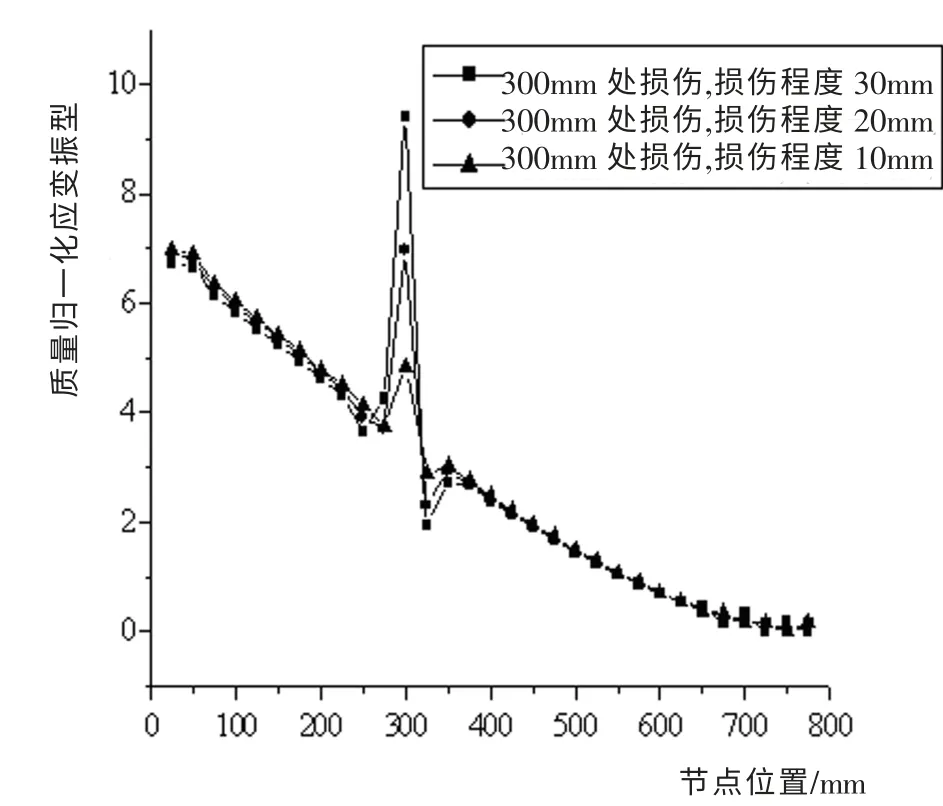
图6 300mm位置损伤处应变振型Fig.6 Strain vibration mode of damaged sites of 300mm

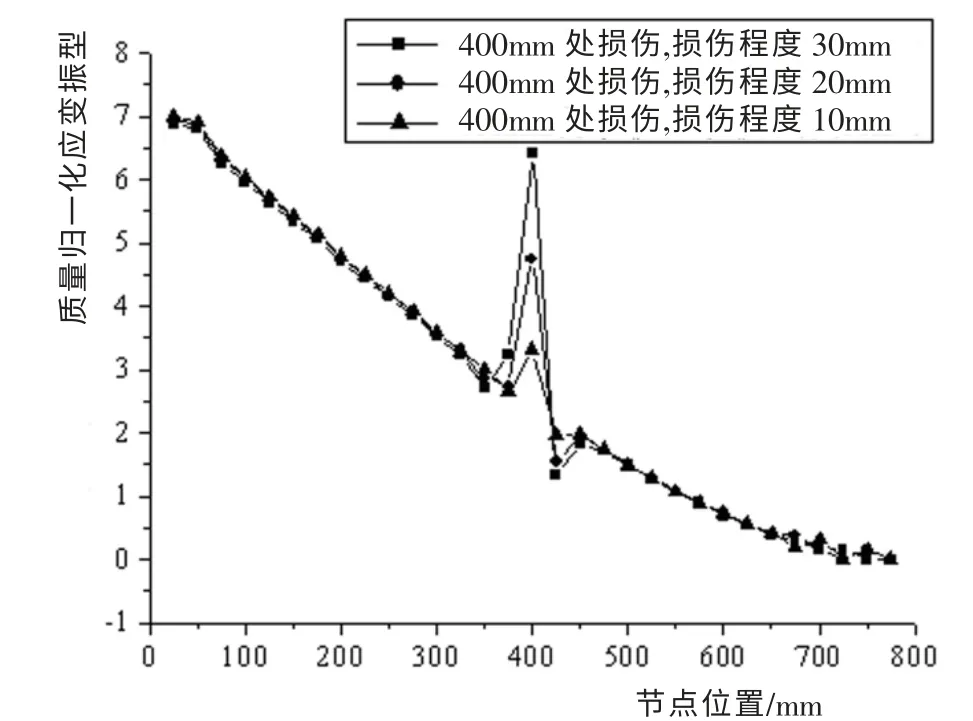
图7 400mm位置损伤处应变振型Fig.7 Strain vibration mode of damaged sites of 400mm

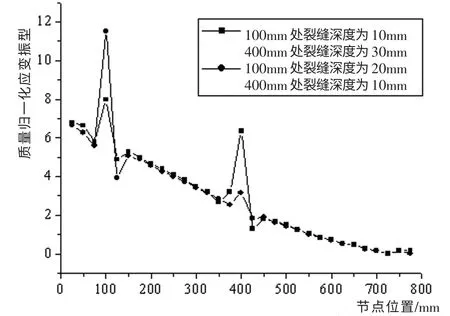
图8 100mm&400mm位置损伤处应变振型Fig.8 Strain vibration mode of damaged sites of 100mm and 400mm

仿真实例中，不同损伤工况的结构位移振型如图9 所示。 显而易见，在各种损伤工况下，损伤节点处的位移振型与没有损伤处的位移振型几乎重叠在一起，没有明显的突变发生。 这说明，借助位移振型不能诊断结构是否损伤。 所以，有限元仿真算例表明，应变模态对结构损伤的敏感程度要远远高于位移模态，应变模态振型可以作为结构损伤的敏感量指标。

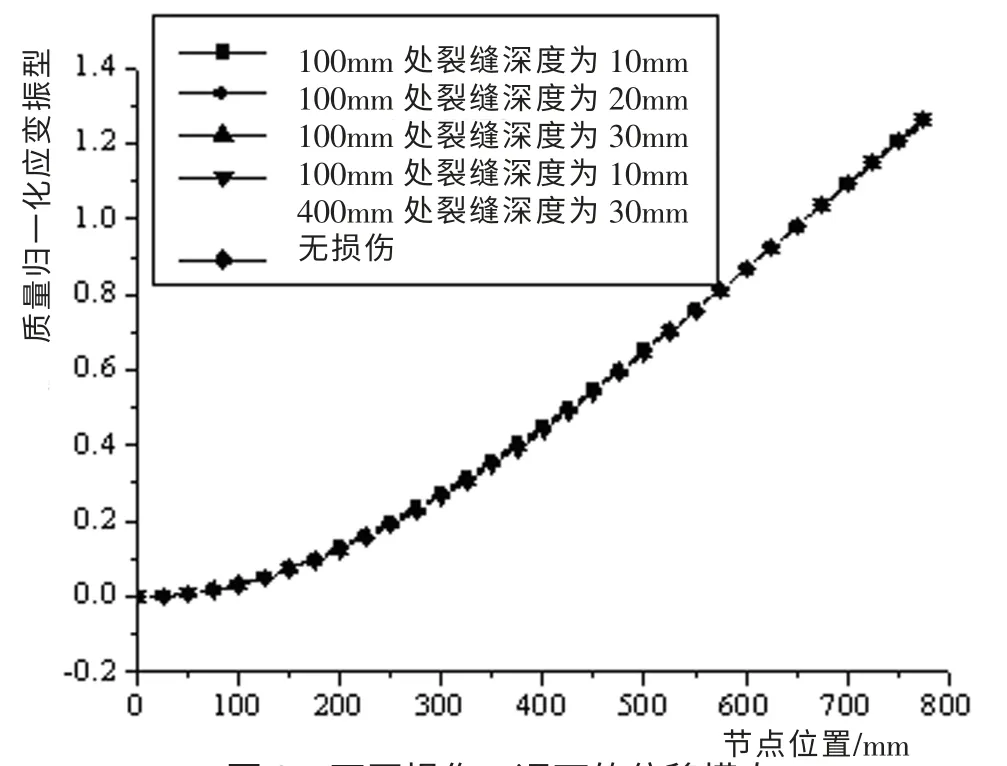
图9 不同损伤工况下的位移模态Fig.9 Displacement mode of different damage conditions

3 结语

综上所述，本文阐述了模态分析的实质及应变模态分析理论，通过振动微分方程与差分方法阐明了位移模态、应变模态与曲率模态三者之间的联系。证明了以结构固有频率作为损伤敏感性指标难以确定结构在早期是否发生损伤和损伤程度，而应变模态振型比位移模态振型更加敏感，可以作为结构损伤诊断的敏感性指标。

[1] 侯立群. 大型斜拉桥基于健康监测的模型修正、 损伤诊断与预警方法[D]. 哈尔滨：哈尔滨工业大学,2009.

[2] 李文雄,陈存恩. 分阶段结构损伤诊断方法[J]. 土木建筑与环境工程,2011,(6):84-89.

[3] 张翌娜,管欣. 基于曲率模态和神经网络的结构损伤识别与仿真[J]. 河南科学,2007, 25(6):971-974.

[4] 张翌娜. 神经网络在结构损伤识别中的应用[J]. 山西建筑,2007（8）:69-70.

[5] 赵卓,王晓阳,梁军. 基于模态分析和神经网络的裂缝损伤识别[J]. 世界地震工程, 2006（2）：104-109.

[6] 张开银,孙峙华,等. 桥梁结构损伤识别的曲率模态技术[J]. 武汉理工大学学报： 交通科学与工程版,2004（6）：855-858.

[7] 邹晓军. 梁桥结构损伤识别的曲率模态技术[D]. 武汉：武汉理工大学,2003.