基于截面优化的张弦桁架形状参数分析

刘树堂，侯贯泽

（1.广州大学 土木工程学院，广东 广州 510006；2.广东博意建筑设计院有限公司，广东 佛山 528312）

0 引 言

张弦桁架的形状参数有跨度、矢跨比、垂跨比、撑杆数等；对于上部拱形桁架为倒三角形的张弦桁架结构，上弦拱梁的横向间距和纵向间距也是重要的结构参数。对于这些形状参数，一般来说跨度是确定的，而其他参数发生改变。文献［1］～［4］中已经研究分析了矢跨比、垂跨比、撑杆数等形状参数的变化对结构应力与变形的影响，得出了一些结论。但是由于应力、变形等与构件截面尺寸大小及结构上的荷载有关，对这些参数的研究缺乏普遍意义，也就是说，只对某个特定张弦桁架结构进行形状参数分析，缺乏统一的衡量标准。另外，已有文献对于这些形状参数的分析并没有在优化理论的基础上进行，因此若把形状参数分析与结构优化结合起来，则对指导实际工程更有意义。

本文中笔者所进行的张弦桁架形状参数分析是以离散变量截面优化为基础，以最小结构质量作为统一衡量标准，探讨了不同跨度下矢高、垂度与最小结构质量的相互关系，从而根据给定的跨度来选取最优的矢高、垂度，所得结论有利于减小工程造价，对工程设计有较大的参考价值。

1 Fibonacci搜索法

文献［5］中详细分析了采用Fibonacci法搜索张弦桁架最优矢高、垂度的可行性。现采用Fibonacci搜索法，以跨度L为100m、垂度为2.8m的上弦为倒三角形桁架的张弦桁架结构为例，其中，恒荷载取1.38kPa。活荷载取0.3kPa，风荷载取0.7kPa，温度荷载取40℃。Fibonacci法搜索最优矢高的具体计算步骤［6－7］为：

（1）参数初始化。文献［8］～［12］中的计算分析结果表明，结构的矢跨比最好大于0.12，这时结构的受力和位移都在比较合理的范围内，并且矢跨比对纵向位移和支座反力的影响不明显。据此确定出矢高的初始搜索区间为［0.10L，0.17L］，因此本算例中矢高的初始搜索区间左端点a＝10m，搜索区间右端点b＝17m。初定矢高允许误差ε为0.01 m，计算目标函数值的次数n，则函数值Fn＋1＞（ba）／ε＝700，从Fibonacci数列可知，F15＝987，F14＝610，故取n＝14。

（2）初始2个搜索点，第1次搜索区间左、右端点函数值fa（1），fb（1）分别为

调入张弦桁架离散变量截面优化程序，经过计算得到第1次搜索区间左、右端点矢高所对应的最小结构质量分别为 wtmina（1）＝88.51t，wtminb（1）＝86.255t。

（3）保留区间和保留点的选择。由于最小结构质量wtmina（1）＞wtminb（1），因此保留区间为［12.68，17］，保留点为xr＝fb（1）＝14.33。取

再比较wtmina（2）与wtminb（2），决定第2次保留区间和保留点。为了简化计算，本文中略去后面步骤说明，根据计算结果得到的矢高与最小结构质量的关系见图1。

图1 矢高与最小结构质量的关系Fig.1 Relation Between Rise and Minimum Structure Weight

从图1可以看出，矢高与最小结构质量的关系曲线大致呈抛物线形状。在结构其他参数不变，满足相同荷载和拓扑形式的情况下，在矢高较小时，最小结构质量较大。这是因为起拱较小时，竖向刚度较小，为了达到结构的位移要求，必须加大杆件截面来提高结构整体刚度。随着矢高的增大，最小结构质量逐渐减小，当矢高为14.87m时，最小结构质量处于抛物线最低点，结构的用钢量达到最小。随着矢高的继续增大，最小结构质量又有所增大，这是因为起拱大，拱长增加，导致了结构的用钢量增加。显然，本特定算例中，最优矢高为14.87m，对应的最小结构质量为85.401t，最优矢跨比为0.148 7。

2 张弦桁架矢高优化分析

2.1 各垂度的张弦桁架矢高优化

上述研究只探讨了跨度为100m、垂度为2.8 m的张弦桁架矢高优化，而相同跨度情况下，不同垂度的张弦桁架最优矢跨比是否相同，这是值得研究的问题。采用笔者编写的形状参数优化程序对不同垂度的张弦桁架进行矢高优化分析，以80，100m的张弦桁架为例，荷载与其他参数设置与第1节中的算例相同，探讨相同跨度下最优矢跨比随垂度变化的规律。

图2中给出了跨度分别为80，100m的张弦桁架在不同垂度下，矢高与最小结构质量的关系曲线。

从图2可以看出：相同跨度情况下，垂度较小时，最优矢高相对较小，但结构的用钢量较大。这主要是因为起拱较小时，索与撑杆夹角较小，施加了预应力的索给撑杆提供的竖向力较小，导致撑杆无法提供给拱很大的竖向力，起不到增加竖向刚度的作用，为了满足结构的位移要求，必须加大索截面面积以提供索拉力，从而为撑杆提供更大的竖向力，这样就导致了结构的用钢量增加。而垂度较大时，索弧长和撑杆长度有所增加，同时为了满足压杆稳定，撑杆截面面积需要增加，导致了结构的用钢量增加。随着垂度的增加，所对应的最优矢高逐渐增加，而结构的用钢量逐渐减小，当垂跨比在0.07左右时，最小结构质量达到最小，即结构用钢量最小；随着垂度的继续增加，所对应的最优矢高反而变小，结构用钢量又有所增大。由此可知，当垂跨比在0.07左右时，才会得到最优矢高与结构用钢量最小。

2.2 各跨度的张弦桁架矢高优化

不同跨度的张弦桁架最优矢跨比是否相同，这是值得研究的问题。根据研究结果，垂跨比在0.07左右时才会得到最优矢高与结构用钢量最小。基于该结论，拟定了60，80，100，125，150m 五种常用跨度的张弦桁架计算模型参数，如表1所示，荷载与其他参数设置与第1节中的算例相同，分别对其进行矢高优化分析。

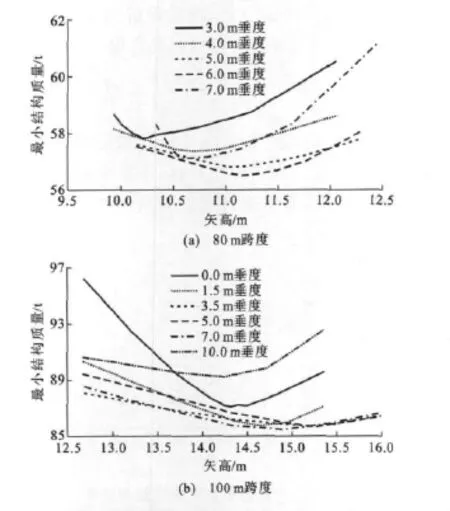
图2 不同垂度下矢高与最小结构质量的关系曲线Fig.2 Relation Curves Between Rise and Minimum Structure Weight Under Different Sags

表1 各跨度张弦桁架结构的模型参数Tab.1 Model Parameters of Different Spans for Truss String Structure m

图3为5种常用跨度的张弦桁架矢高优化结果。其中，图3（a）为5种跨度的矢高优化曲线汇总，图3（b）～（f）分别为5种跨度的矢高与最小结构质量关系曲线。从图3可以看出：

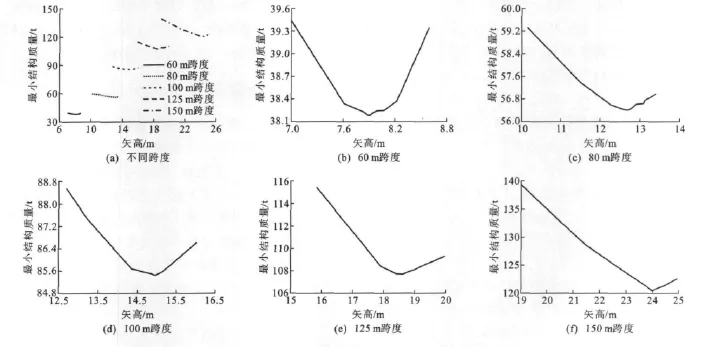
图3 不同跨度下矢高与最小结构质量的关系曲线Fig.3 Relation Curves Between Rise and Minimum Structure Weight Under Different Spans

（1）随着跨度的增加，张弦桁架最优矢高逐渐增大［图3（a）］。这主要是因为随着跨度的增加，为了满足结构位移条件等要求，起拱必须有所增加，即矢高必须相应增加，这必然会导致最优矢高随着跨度的增大而增加。

（2）各跨度的矢高与最小结构质量的关系曲线大致呈抛物线形状［图3（b）～（f）］。各跨度在矢高很小时，结构的用钢量都较大；随着矢高增加，结构的用钢量逐渐减小；随着矢高继续增加，结构的用钢量又有所增加。

把张弦桁架各跨度对应的最优矢高绘制成图4。从图4可以看出，最优矢高随着跨度增大而几乎呈线性增加。表2中给出了各跨度所对应的最优矢高与矢跨比。从表2可以看出：当垂跨比为0.07时，各跨度的最优矢跨比出现在0.132～0.159之间；跨度越大时，最优矢跨比稍微偏大，如当跨度为150m时，最优矢跨比为0.154。而最优矢跨比与垂跨比之和为0.22时，结构的质量最小。

图4 最优矢高与跨度的关系曲线Fig.4 Relation Curve Between Optimum Rise and Span

表2 各跨度对应的最优矢高与矢跨比Tab.2 Optimum Rises and Rise－span Ratios of Different Spans

3 张弦桁架垂度优化分析

3.1 各矢高的张弦桁架垂度优化

实际工程中，相同跨度、垂度的张弦桁架也有多种矢高可以选取。在相同跨度情况下，最优垂跨比随着矢高的不同将有着怎样的变化规律，这是值得研究的问题。以跨度80，100m的张弦桁架为例，对不同矢高的张弦桁架进行垂度形状参数优化分析，探讨在相同跨度情况下，最优垂跨比随着矢高变化的规律。

图5中给出了跨度分别为80，100m的张弦桁架在不同矢高下，垂度与最小结构质量的关系曲线。

图5 不同矢高下垂度与最小结构质量的关系曲线Fig.5 Relation Curves Between Sag and Minimum Structure Weight Under Different Rises

从图5可以看出，相同跨度情况下，矢高较小时，最优垂度相对较大，而且最小结构用钢量也较大。这主要是因为矢高较小时，起拱较小，竖向刚度较小，为了达到结构的位移要求，必须加大杆件截面来提高结构整体刚度。而当矢高较大时，起拱较大，拱长增加，这又导致结构的用钢量增加。随着矢高的增加，所对应的最优垂度逐渐减小，而且结构的用钢量逐渐减小，当矢跨比在0.14左右时，最小结构质量达到最小，即结构的用钢量最小；随着矢高的继续增加，所对应的最优矢高反而变大，结构的用钢量又有所增大。由此可知，当矢跨比在0.14左右时，才会得到最优垂度与结构的用钢量最小。

3.2 各跨度的张弦桁架垂度优化

张弦桁架的最优垂度随跨度变化的规律如何，而且不同跨度的张弦桁架最优垂跨比是否相同，这是值得进一步研究的问题。根据研究结果，矢跨比在0.14左右时才会得到最优垂度与最小结构用钢量。基于该结论，笔者拟定了60，80，100，125，150 m五种常用跨度的张弦桁架计算模型参数（表1），并分别对其进行垂度形状优化分析。

图6为5种常用跨度的张弦桁架垂度优化结果。其中，图6（a）为5种跨度的垂度优化曲线汇总，图6（b）～（f）分别为5种跨度的垂度与最小结构质量关系曲线。

图6 不同跨度下垂度与最小结构质量的关系曲线Fig.6 Relation Curves Between Sag and Minimum Structure Weight Under Different Spans

从图6可以看出：

（1）随着跨度的增加，最优垂度逐渐增大。这主要是因为随着跨度的增加，为了满足结构位移约束条件，起拱必须有所增加，这样才能使施加了预应力的索给撑杆提供足够大的竖向力，即垂度必须相应增加，这必然会导致最优垂度也将随着跨度的增大而增加［图6（a）］。

（2）各跨度的垂度与最小结构质量的关系曲线大致呈抛物线形状［图6（b）～（f）］。各跨度在垂度较小时，结构的用钢量都较大；随着垂度增加，结构的用钢量逐渐减小；随着垂度继续增加，结构的用钢量又有所增加。

把张弦桁架各跨度对应的最优垂度绘制成图7。从图7可以看出，最优垂度随着跨度增大而几乎呈线性增加。表3中给出了各跨度对应的最优垂度与垂跨比。从表3可知：当矢跨比在0.14左右时，各跨度的最优垂跨比出现在0.07左右；最优的垂跨比与矢跨比之和为0.22，此时结构的质量最小。

4 结语

（1）对张弦桁架的矢高、垂度进行了优化分析。优化分析结果表明，当垂跨比在0.07左右时，才会得到最优矢高与最小结构质量，各跨度的最优矢跨比出现在0.132～0.159之间，跨度越大，最优矢跨比稍有增加。最优的矢跨比与垂跨比之和为0.22，此时结构的质量最小。

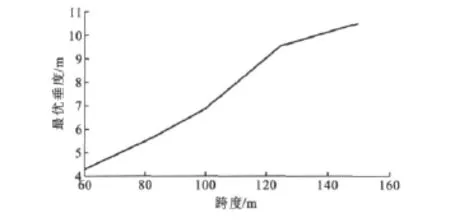
图7 最优垂度与跨度的关系曲线Fig.7 Relation Curve Between Optimum Sag and Span

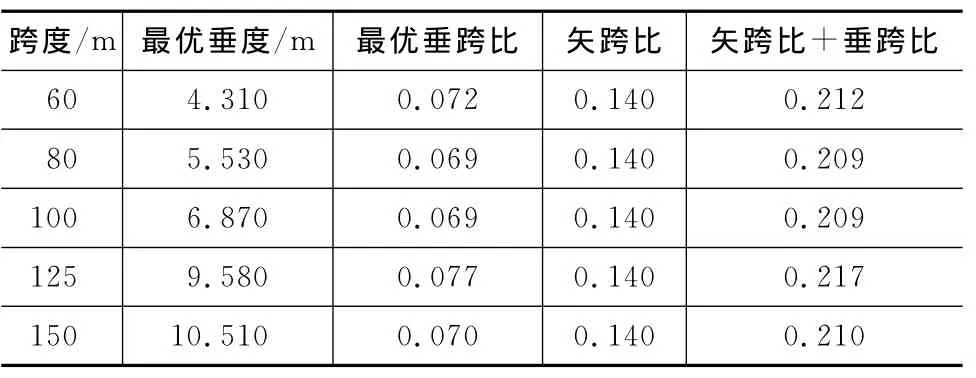
表3 各跨度对应的最优垂度与垂跨比Tab.3 Optimum Sags and Sag－span Ratios of Different Spans

（2）当矢跨比在0.14左右时，才会得到最优垂度与最小结构质量。随着跨度的增加，最优垂度随着跨度增大而几乎呈线性增加；各跨度在垂度很小时，结构质量都较大，随着垂度增加，结构质量逐渐减小，随着垂度继续增加，结构质量又有所增加；当矢跨比在0.14左右时，各跨度的最优垂跨比出现在0.07左右。

［1］XUE W C，LIU S.Design Optimization and Experimental Study on Beam String Structures［J］.Journal of Constructional Steel Research，2009，65（1）：70－80.

［2］杨 睿.预应力张弦梁结构的形态分析及新体系的静力性能研究［D］.杭州：浙江大学，2001.

YANG Rui.Shape Analysis of Prestressed BSS and Study of Mechanical Behavior for a New System［D］.Hangzhou：Zhejiang University，2001.

［3］陈 侃.预应力张弦拱结构的理论分析和受力特性研究［D］.杭州：浙江大学，2000.

CHEN Kan.Theoretical Analysis and Mechanics Property Study of Prestressed Beam String Structure［D］.Hangzhou：Zhejiang University，2000.

［4］马美玲.张弦梁结构找形和受力性能研究［D］.杭州：浙江大学，2004.

MA Mei－ling.Study of Form－finding and Mechanical Behavior for Beam String Structure［D］.Hangzhou：Zhejiang University，2004.

［5］曹春阳，刘红艳，董锦坤.离散变量结构优化的斐波那契算法［J］.辽宁工学院学报，2005，25（1）：34－36.

CAO Chun－yang，LIU Hong－yan，DONG Jin－kun.Fibonacci Design Method for Structure Optimization with Discrete Variables［J］.Journal of Liaoning Institute of Technology，2005，25（1）：34－36.

［6］SUBASI M，YILDIRIM N，YILDIZ B.An Improvement on Fibonacci Search Method in Optimization Theory［J］.Applied Mathematics and Computation，2004，147（3）：893－901.

［7］YILDIZ B，KARADUMAN E.On Fibonacci Search Method with k－Lucas Numbers［J］.Applied Mathe－matics and Computation，2003，143（2／3）：523－531.

［8］王秀丽，刘永周.矢跨比和垂跨比对张弦立体桁架性能的影响分析［J］.空间结构，2005，11（1）：35－39.

WANG Xiu－li，LIU Yong－zhou.Influences of Rise－tospan Ratio and Sag－to－span Ratio on the Prestressed Spatial Truss String Structure［J］.Spatial Structures，2005，11（1）：35－39.

［9］姚国红，刘树堂，康丽萍.单榀张弦桁架结构各因数的影响分析［J］.河南科技大学学报：自然科学版，2008，29（2）：65－70.

YAO Guo－hong，LIU Shu－tang，KANG Li－ping.Influence Analysis of Factors of Single Truss String Structure［J］.Journal of Henan University of Science ＆Technology：Natural Science，2008，29（2）：65－70.

［10］柯友华，陈 波.张弦桁架结构的非线性地震响应及其参数分析［J］.钢结构，2010，25（3）：37－44.

KE You－hua，CHEN Bo.The Nonlinear Seismic Response and Parametric Analysis of Truss String Structure［J］.Steel Construction，2010，25（3）：37－44.

［11］韩万水，王 涛，李永庆，等.大跨钢桁架悬索桥有限元模型实用修正方法［J］.交通运输工程学报，2011，11（5）：18－27.

HAN Wan－shui，WANG Tao，LI Yong－qing，et al.Practical Updating Method of Finite Element Model for Long－span Steel Truss Suspension Bridge［J］.Journal of Traffic and Transportation Engineering，2011，11（5）：18－27.

［12］高 亮，刘健新，张 丹.桁架桥主梁三分力系数试验［J］.长安大学学报：自然科学版，2012，32（1）：52－56.

GAO Liang，LIU Jian－xin，ZHANG Dan.Experimental Study on Three－component Force Coefficients of Truss Girder Cross－section［J］.Journal of Chang’an University：Natural Science Edition，2012，32（1）：52－56.