基于两种数学模型的坐标系统转换的比较

陶叶青,杨 娟,赵 强

1.中国矿业大学国土环境与灾害监测国家测绘局重点试验室，江苏徐州，221116；2.宿州学院煤矿勘探工程技术研究中心，安徽宿州，234000

基于两种数学模型的坐标系统转换的比较

陶叶青1，2,杨 娟2,赵 强2

1.中国矿业大学国土环境与灾害监测国家测绘局重点试验室，江苏徐州，221116；2.宿州学院煤矿勘探工程技术研究中心，安徽宿州，234000

针对坐标系统转换是测量作业与生产中经常遇到的问题，首先对四参数模型与七参数模型在坐标系统转换中的应用进行分析和探讨，然后在此基础上通过对已知数据分别应用四参数模型与七参数模型进行坐标系统转换，并对坐标系统转换进行比较。结果表明:在较大区域范围内，七参数模型的坐标系统转换精度要比四参数模型的转换精度高；四参数模型更适用于参心坐标系与地心坐标系之间的转换。

坐标系统；四参数模型；七参数模型；转换精度

随着原始测绘资料的大量积累和测绘技术的迅速发展以及坐标系统的更新换代，在实际工作中，经常需要对坐标系统进行转换。国内坐标系统转换主要包括两个方面：第一，参心坐标系统(北京54坐标系统、西安80坐标系统)向新一代地心坐标系统的转换(CGCS200)；第二，在GNSS所对应的坐标参考框架下获得的观测成果向我国坐标系统下成果的转换。

坐标系统转换的基本原理是根据相同控制点在不同坐标系统的坐标对坐标转换数学模型的转换参数进行求解，应用求解出参数的转换模型解算某一坐标系统下的控制点在另外一种坐标系统下的未知坐标。常用的转换模型主要有基于平面的四参数模型[1]与基于空间的七参数模型[2]。当控制点数目大于必要观测数时，则应用最小二乘准则(Least Squares，LS)建立高斯-马尔可夫模型(Gauss-Markov，G-M)求解模型参数。测绘工作者通常对建立G-M模型的准则进行讨论，对应用总体最小二乘准则(Total Least Squares，TLS)和不等式约束准则(Inequality Constraints，IC)建立G-M模型的方法进行比较并得出有益的结论[3-4]。应用七参数模型实现参心坐标系向地心坐标系的转换，需要控制点的空间三维直角坐标。由于控制点在参心坐标系中缺乏高精度的大地高信息，导致无法精确获得控制点在参心坐标系中的空间三维直角坐标。为解决控制点在参心坐标系中缺乏高精度的空间三维直角坐标对转换参数求解的影响，文献[5]～[7]对此问题进行了讨论，并得出有益结论。应用四参数模型实现坐标系统的转换，需要控制点的平面坐标。由于应用GPS观测得到的是控制点的空间三维直角坐标(差)，将空间三维直角坐标转为平面坐标时，会产生一定的变形。为减小由空间三维直角转换为平面坐标时产生的变形，文献[8]对选择合适的投影面实现坐标的转换进行了讨论。

本文对应用四参数转换模型与七参数转换模型实现坐标系统转换分别进行阐述，对不同模型在转换区域与转换精度上进行比较，并通过算例对坐标转换模型的算法进行实现。

1 转换模型

1.1 四参数转换模型

基于平面的坐标系统转换数学模型为：

(1)

式中(x1，y1)、(x2，y2)为不同坐标系统下的平面坐标，(ab)T为平移参数，α为旋转参数，λ为尺度参数。转换模型的参数通过在不同坐标系中进行控制测量，获得公共点在不同坐标系中的平面坐标(x1，y1)、(x2，y2)；当控制点数量多于两个时(即存在多余观测),按最小二乘法求解转换参数。

应用GNSS进行控制测量，获得的是控制点在WGS-84坐标系统下的空间三维直角坐标(差)，即控制点间的基线向量；应用四参数模型进行坐标系统的转换，须将控制点的空间三维直角坐标转换为平面坐标：先将空间三维直角坐标转换为大地坐标，再将大地坐标按高斯-克吕格投影正算获得平面坐标。

1.2 七参数转换模型

基于空间的坐标系统转换数学模型为：

(2)

式中(X1、Y1、Z1)T与(X2、Y2、Z2)T为控制点在不同坐标系中空间三维直角坐标，平移参数为(X0、Y0、Z0)T、旋转参数为(εX,εY,εZ)、尺度参数为δμ。转换模型的参数通过在不同坐标系中进行控制测量，获得公共点在不同坐标系中的空间三维直角坐标(X1、Y1、Z1)T与(X2、Y2、Z2)T；当控制点数量多于两个时(即存在多余观测),按最小二乘法求解转换参数。

运用七参数模型对我国参心坐标系进行转换时，由于控制点在参心坐标系的坐标是以二维坐标(大地坐标或平面坐标)与高程表示的，因此，须将二维坐标转换为空间三维直角坐标：先将平面坐标按高斯-克吕格投影反算获得大地坐标，再将大地坐标转换为空间三维直角坐标。此过程中,需要高精度的控制点大地高信息，但由于参心坐标系都是用光学方法构建的，控制点缺乏高精度的大地高[2]。因此，控制点在参心坐标系中的空间三维直角坐标精度不高。

2 算例与分析

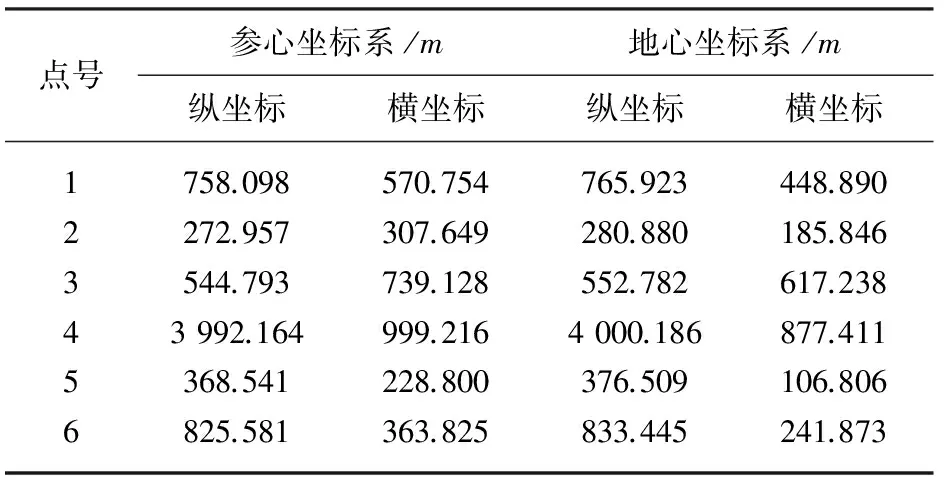
表1 控制点在不同坐标系中的平面坐标

应用已知数据(表1)中的1、2、3号点作为已知点计算转换参数；应用4、5、6号点作为检核点。模型的内符合精度以单位权方差(式(3))作为评价标准[9]：

(3)

外符合精度以点位中误差(式(4))做为评价标准[9]:

(4)

分别应用四参数模型与七参数模型进行坐标系统的转换，获得模型的内符合精度与外符合精度，如表2。

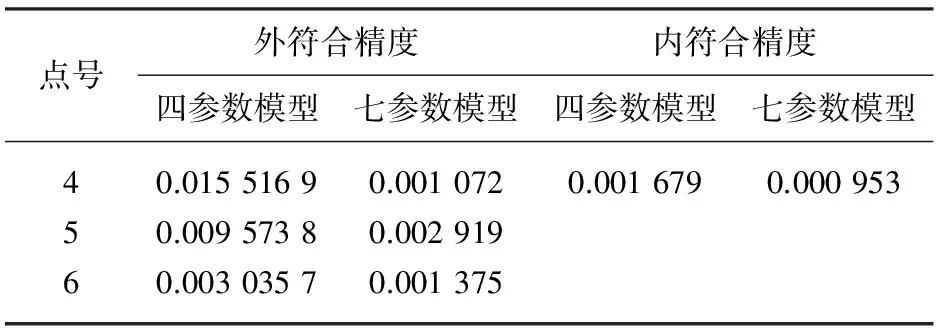
表2 两种转换模型的转换精度

内符合精度(式(3))是模型含有多大模型误差的表征。应用七参数模型实现坐标系统的转换，无需顾及坐标在投影过程中引起的投影变形的影响；而应用四参数模型则无法顾及由空间三维直角坐标投影至平面时引起的投影变形。表2中，七参数模型的内符合精度高于四参数模型的内符合精度，说明七参数模型更适用于坐标系统的转换。

外符合精度(式(4))是经模型转换后的控制点点位精度的表征。外符合精度的高低，除受转换模型自身适用性程度的影响外，控制点中含有的固有误差也影响其转换精度。表2中，七参数模型的外符合精度高于四参数模型的外符合精度，说明七参数模型更加适用。不同控制点的外符合精度的大小不同，表明控制点含有的固有误差大小不一。

四参数模型虽然转换精度不及七参数模型，但是，它用于我国参心坐标系与地心坐标系之间的转换更有理论依据。我国的参心坐标系由于控制点缺乏精确的大地高信息，导致控制点的空间三维直角坐标无法精确获得，因此，应用七参数模型转换缺乏数据基础。

3 结 论

本文在对两种常用坐标系统转换模型的转换原理进行讨论的基础上，通过已知数据对其转换精度进行分析。结果表明：(1)七参数转换模型的转换精度高于四参数转换模型；(2)七参数模型无需顾及控制点由空间三维直角坐标投影至平面时引起的变形误差；(3)由于我国参心坐标系的控制点大地高精度不高，四参数模型更加适用于参心坐标系向地心坐标系的转换。

[1]姚宜斌．平面坐标系统相互转换的一种简便算法[J]．测绘与信息工程，2001(1)：1-3

[2]施一民．现代大地控制测量[M]．北京：测绘出版社，2003：5-100

[3]刘立龙，姚朝龙.LS和TLS在平面坐标转换中的应用[J].测绘科学,2012，37(5)：12-14

[4]陶叶青，杨娟．基于不等式约束的顾及长度变形的坐标系统转换方法[J]．测绘通报，2013(2)：51-53

[5]王解先，邱杨媛．高程误差对七参数转换的影响[J]．大地测量与地球动力学，2007，27(3)：25-27

[6]王解先，王军，陆彩萍．WGS-84与北京54坐标的转换问题[J]．大地测量与地球动力学，2003，23(3)：70-73

[7]谢鸣宇，姚宜斌．三维空间与二维空间七参数转换参数求解新方法[J]．大地测量与地球动力学，2008，28(2)：104-109

[8]陶叶青，黄淑玲，杨娟，等．一种适合单基站CORS平面坐标系统转换的方法[J]．测绘科学，20012，37(3)：116-117

[9]武汉大学测绘学院测量平差学科组．误差理论与测量平差基础[M]．武汉：武汉大学出版社，2003：102-185

(责任编辑：汪材印)

ComparisonofCoordinatesTransformationBasedonTwoMathematicalModels

TAO Ye-qing,YANG Juan, ZHAO Qiang

1.China University of Mining and Technology,Key Laboratory for Land Environment and Disaster Monitoring of SBSM，Jiangshu Xuzhou，221116;2.Engineering Research Center of Coal Mining Exploration,SuZhou University,Anhui Suzhou，230000，China

coordinates transformation is the main problem in the survey work. Four parameters model and seven parameters model are in use frequently of the many transformation models. On the basis of discussion the methods of four parameters model and seven parameters model for coordinate conversion, applies the known data to compare the accuracy of two conversion models. The result appears that seven parameters model is more accurate than four parameters model, and four parameters model is more suitable for conversion between reference-ellipsoid-centric coordinate and geocentric coordinates.

Coordinates system;Four parameters model;Seven parameters model;Transformation Accuracy

10.3969/j.issn.1673-2006.2013.09.021

P228

A

1673-2006(2013)09-0078-03

2013-04-09

安徽省煤矿勘探工程技术研究中心开题课题资助“矿区坐标系统一致性改造的区域性椭球实现方法”(2013YKF03)，宿州学院硕士科研启动基金资助“高层建筑物变形监测与预计分析”(2013yss01)。

陶叶青(1984-)，江苏淮安人，硕士，助教，主要研究方向：测量数据处理。