水利工程投标报价博弈在合成标底评标中的应用

王 月，李东亮，李永亮

（1.河北工程大学，资源学院 河北 邯郸056000；2.辽宁省东水西调工程建设局，辽宁 沈阳110000；3.河南华北水电工程监理有限公司，河南 郑州450011）

0 引言

目前我国大部分工程项目评标标底都采用合成的方法。 合成标底评分法是一种定量化的评分办法，其基本做法是：（1）甲方先按一定的方法编制出甲方标底，超出甲方标底一定范围的投标报价为无效报价，其余均为有效报价。 （2）再将甲方标底和所有有效报价的平均数按一定比重加权求和，计算出合成标底。 （3）根据合成标底对投标方的报价进行评分，报价在合成标底的一定范围内时得满分，超出或低于某个值时以百分点为单位进行扣分[1～2]。

一般而言，合成标底评标与无标底评标在评标上方法是一致的，只是在最优报价的确定上有所不同[3]。 前者的最优报价按一定规则对各投标人报价进行合成，而后者的最优报价（即合成标底）是在考虑各投标人报价的同时还要预测甲方标底，较为复杂。 本文试结合有关实际工程案例，对报价博弈在水利工程投标报价合成标底评标中的应用进行探讨。

1 合成标底投标报价博弈模型建立

1.1 投标报价条件描述

为了便于描述，设甲方标底为单位1，投标报价均用以甲方标底为基数的相对数表示。 同时，规定以下内容：

（1）甲方标底为1，占合成标底中的比重为λ（0＜λ＜1）。

（2）投标方报价处于甲方报价的[a，b]时，为有效报价，其平均数占合成标底的比重为1-λ。

（3）投标方报价在合成标底的[c，d]时，得满分，超出d 或者低于c 时，每个百分点分别减p 分或q 分。

（4）设定变量n、A、B、M、N，其中，n 为有效投标的数量；A 为我方报价；B 为其余n-1 个有效报价的平均数；M 为合成标底；N 为我方报价的扣分。

1.2 报价参数假设

为了科学地制订报价，使自己在获利最大和得分最高之间取得平衡，作如下假设：（1）采用的定额编制方法已知，可据此自行估算出标底的绝对数，不妨设其为Y；（2） 文件中已经明确规定了λ、a、b、c、d、p、q 的值，即它们是已知的常数；（3）报价处在得分最高但未能得到满分的情况下；（4）虑成本、技术、质量、资信、任务饱满度等因素的影响。

1.3 报价模型的建立

1.3.1 合成标底

根据评标办法及相关文献的研究成果[4]，设置公式为：

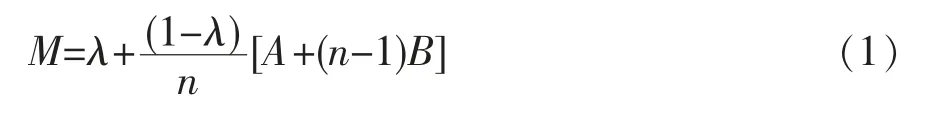
1.3.2 扣分公式

扣分公式为

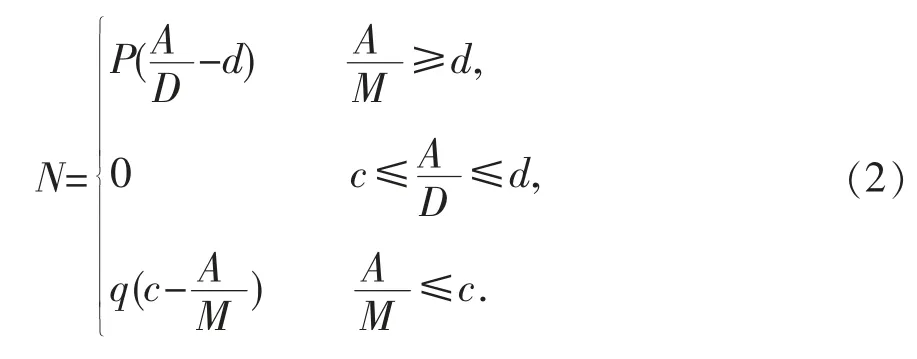
1.3.3 博弈原则

我方报价的目标是中标与获利，因此，博弈原则是得益最大化[5]。 在扣分最少的前提下，报价尽可能高，并且能够保证以最大的概率中标。 也就是说，投标人的投标报价要同时满足下列两个条件：

1.3.4 满分报价区间

由前面的假设条件（3）可知，要中标，只需考虑得满分的报价区间。 实际上，这样做缩小了中标的报价区间。 因为在实际报价中，可能存在所有投标者都未能得到满分而由最高分中标的情况。 但是，在绝大多数情况下，满分报价区间是有解的，求出满分报价区间，就足以使投标者满足，没有必要再去求解其余的报价中标区间。

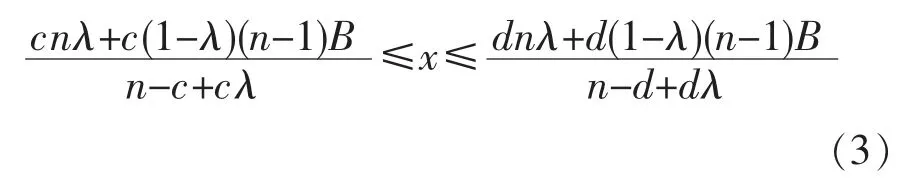
由决策原则A→max，得出最优报价公式：

1.4 讨论

因为B 是其他n-1 家有效投标者报价的平均数，可以视为随机分布；n 是有效报价的数目，在评标前也是未知数。 故我方可以对n 和B 的取值范围作大致的估计，设B∈[B1，B2]，n∈[n1，n2]，欲使我方报价x 在上述估计范围都能得满分，对于所有取值范围内的B 和n，x 的满分报价区间下限的最大值必须小于或等于上限的最小值。 令

则对于给定范围内的B，n 都能得满分的x 有解的判断条件为:F1（n，B）≤F2（n，B）。

将F1（n，B），F2（n，B）分别对B，n 求导，可得：

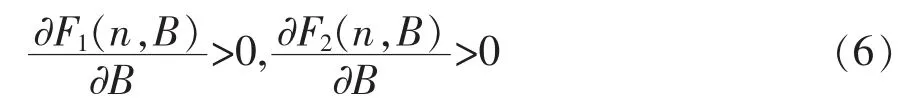
所以，F1（n，B），F2（n，B）是B 的增函数。

所以，当B(1-c+cλ)-c2λ＞0 时，F1（n，B）是n 的增函数；

当B(1-c+cλ)-c2λ＜0 时，F1（n，B）是n 的减 函数。

故，当B(1-d+dλ)-d2λ＞0 时，F2（n，B）是n 的增函数；

当B(1-d+cλ)-d2λ＜0 时，F2（n，B）是n 的减函数。

因而在给定B，n 的范围内，A 都是最优解的判断准则，相应的最优解如表1 所示。

表1 最优报价分段讨论表Table 1 Optimal bidding subsection discussion

说明：在实际应用此模型的过程中，可以根据招标文件中给定的c、d、λ 计算出前提条件中的临界值。 因为B 是有效报价的平均值，故a≤B≤b。 结合此条件判断表中的分段条件，利用相应的判断准则，即可求得在各段内我方的最优报价。

1.5 最优报价决策

在前面，已经给出了我方报价的满分区间和最优报价公式。 但是，不论是满分报价区间还是最优报价公式，都是B 和n 的函数。 而B 和n 都是在投标前无法准确确定的，它们随其他各个投标人报价的变化而变化。在1.4 中的讨论中，又用分段讨论的方法进行了更深入的研究，在每个区间段上能够计算出一个确切的最优报价值。 如何从这几个值中选出一个最恰当的值，就是即将讨论的最优报价决策问题。

最优报价决策的关键是确定B 和n 的大致范围，亦即B1、B2、n1、n2的值。 对于n，一般可以根据参与投标的人数和当时的具体情况，很容易估计出大致的范围。 如果参与人数不多，我们甚至可以假定n1=3，n2=总人数（因为若有效投标数小于3，则必须重新投标）。对于B，通常有两种办法：一是可以根据经验，结合招标文件中对有效投标范围和得满分的范围的规定，确定B 分布在各区间段的概率，再选择概率最大的区间段，以此区间段上的最优报价作为最终报价；二是根据对称的假设（即假定所有的投标人作为投标博弈的局中人，他们所掌握的信息、思维方式都是对称的），来确定B 值。 具体的思维过程和做法如下：

（1）先假定其他人同我方一样思考，他们也都掌握了前面所说满分报价区间和最优报价计算公式，并以此作为他们报价的依据。（2）假定B 在区间段[x1,x2]上，利用判断准则，进一步确定B 在[x3，x4]上，其中x1≤x3≤x4≤x2，求出最优取值A。 因为其他投标人也会和我们做同样的推理，他们在此区间段上也能得出同样的最优报价A。 这样，其他人都做出A 的报价，而B 是我方以外其他所有人的有效报价平均数，故应该有B≈A。 所以，如果求出的本区间段上的最优报价A 落在区间[x3，x4]外，就说明在对称假设下，B 落在[x3，x4]外。与求出A 的假设（即B在[x3，x4]上）相矛盾。 此路不通，只能讨论下一个区间段。如果A 在[x3，x4]上，则说明此时的A 就是最终报价。

2 合成标底博弈模型实例分析

某水库除险加固项目进行施工招标，共有8 家施工单位通过资格预审参加投标。 标底是采用该省定额编制方法编制的。 招标文件中规定：经济标的评分办法采用合成标底法，满分为30 分，甲方标底占合成标底的70%，投标单位有效报价的平均数占合成标底的30%； 投标单位报价为甲方标底的90%～101%时为有效报价；扣分原则是报价在合成标底的98%～100%时得满分，超过100%时，每超过1%扣2分，低于98%时，每降低1%扣1 分。

2.1 计算我方投标报价

已知：此例中甲方标底占合成标底比重λ=0.7，投标方有效报价区间为[0.90，1.01]，即a=0.90、b=1.01；报价满分的区间[0.98，1.00]，即c=0.98、d=1.00。将各参数代入式（1），得出合成标底：

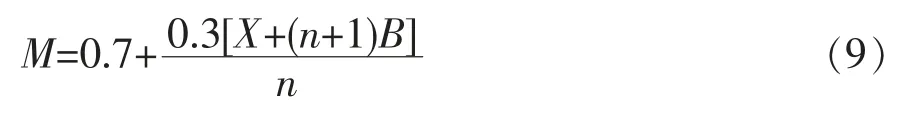
将（9）式代入（3）式，得出满分报价区间：

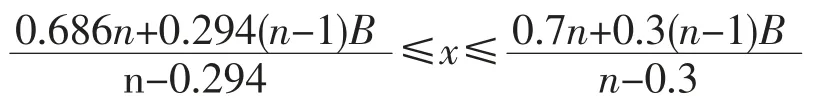
根据专家意见及经验，不妨设n∈[n1,n2]=[3,8]此时，

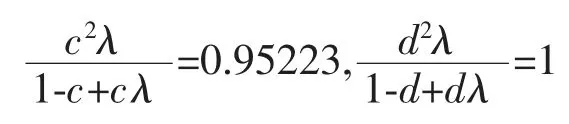
分段讨论如下：

（1）如果B∈[0.90，0.95223]，即0.90≤B1≤B2≤0.95223，则判断准则为F1(3，B2)≤F2(8，B1)。 F1是B1的增函数，而B2≤0.95223，所以有解B1≥0.88064。当B∈[0.90，0.95223]时，最优报价为A=0.96745。但由于A＞0.95223，所以A=0.96745 不是最终报价。

（2）如果B∈[1，1.01]，显然是小概率事件，可不予考虑。

（3）如果B∈[0.95223，1]，即0.95223≤B1≤B2≤1，则判断准则为F1(8，B2)≤F2(8，B1)。F1是B1的增函数，而B2≤1，所以有解B1≥0.96357。 则当B∈[0.95223，1]时，最优报价为A=0.99006。 因为A=0.99006∈[0.95223，1]，所以A=0.99006 是我方的最终报价。

根据博弈原则，取A=0.99006Y，即我方按0.99006作出报价，而其他投标方有效报价的平均数只要在[0.95223Y，Y]范围，我方就一定获得满分(当然，也不排除其他投标方和我方一样获得满分)。经过认真编制预算，我们估算出的标底Y 为108 118 276.7元。 因此，我方的报价为108 118 276.7 元×0.99006=107 043 581 元。

2.2 博弈效果分析

开标后，得知该工程甲方标底为110 529 089元，其他各投标方报价如表2 所示。

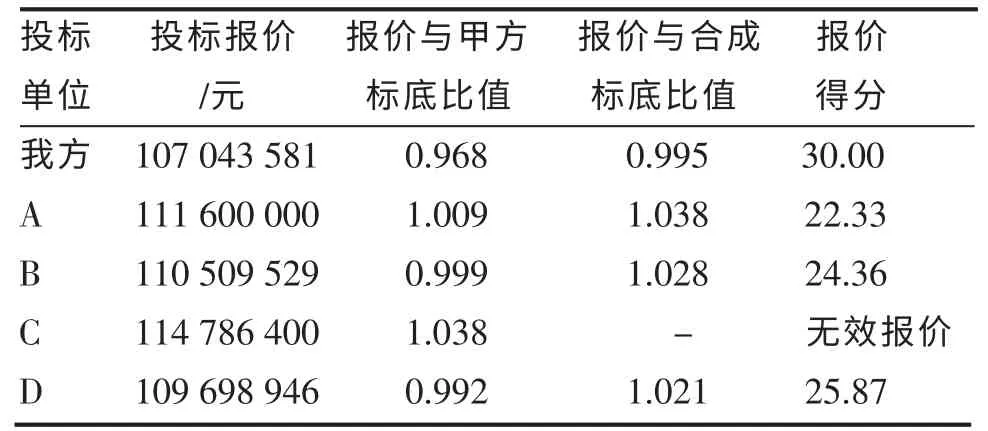
表2 各投标人报价得分表Table 2 Bidders offer scores

从表2 中可以得知，我方报价取得了满分，比次高分高出近5 分。 由此可见，我方利用博弈模型辅助进行投标报价的决策取得了一定成果。 由于我方在施工方案、施工管理、企业信誉等各方面均不亚于其他竞争对手，因此，我方能够凭借各方面实力赢得该工程。

3 结语

该报价博弈模型不仅对投标报价策略进行了理论研究，而且也通过水电工程投标竞标实践，使投标人在得满分的报价区间内的最终报价。 其中，合成标底中参数的设定以及其他条件的改变等都会改变模型的具体形式，但模型建立的基本思想是不变的，从这种意义上可以说，建立投标报价博弈模型具有比较广泛的应用价值。

[1] 黄宏飞,欧国立.博弈论在投标报价决策中的应用[J].北京交通大学报，2000，24（3）：41-43.

[2] 何增勤.工程项目投标策略[M].天津:天津大学出版社，2004.

[3] 宋维佳,张巍.基于先验信息的无标底投标报价策略研究[J].预测（FORECASTING）,2007,26（1）:33-37.

[4] 蓝柏雄,程佳慧,陈秉正. MBA 工商管理硕士课程系列教材:管理数学(下)——运筹学［M］.北京：清华大学出版社，1997.

[5] 郝丽萍,谭庆美,戈勇.基于博弈模型和模糊预测的投标报价策略研究[J].管理科学学报，2002（3）：94-96.