具线性耗散摩阻力的圣维南方程组Cauchy问题探讨
李文丰,聂大勇
(黄河水利职业技术学院,河南 开封 475004)
0 引言
天然河流、引水和灌溉渠道、人工运河以及许多水工建筑物中的流动都属于明渠流动,是自然界和人类现实生活中最常见的一种流动。 由于生产实践和人类生活的需要,对明渠流动的研究和认识具有悠久的历史。 1769 年谢才(A.de Chézy)建立的明渠均匀流公式一直沿用至今。 近年来,科技的进步和生产的发展使人们不仅需要了解明渠流动中断面的平均流速,还需要知道流速及其他有关物理量在时间和空间上的分布,从而推进了对明渠紊流的研究。 河道一维非恒定流作为比较常见的明渠紊流,其研究也受到越来越多的关注。
河道一维非恒定流一般都采用圣维南(Saint-Venant)方程进行描述。 圣维南方程在水力学研究和实践中得到证实和完善,并且已在水利工程实践中得到广泛应用[1]。 众所周知,圣维南方程组是一个典型的一阶拟线性双曲型方程组,目前的研究主要局限于方程本身和计算方法[2~3],而对其经典解的存在性和非存在性研究比较少[4]。 如李大潜研究了其边界的精确能控性[5],刘法贵等研究了具高阶耗散的圣维南方程组的Cauchy 问题[6]。
本文探讨了具线性耗散摩阻力的圣维南方程组,利用局部解延拓的方法得到了整体经典解的存在性,验证了一阶拟线性双曲方程组低阶耗散可以保证整体经典解的存在性,并给出了解发生破裂的一个充分条件。
1 一致先验估计
1.1 预备知识
如下具线性耗散摩阻力的一维圣维南方程组的Cauchy 问题[5]:
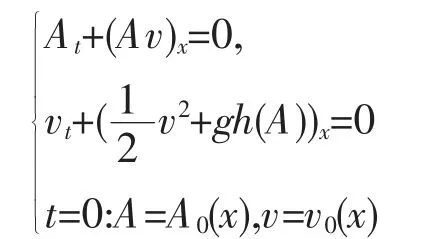
式中:A=A(t,x)为时刻t、位置x 处过水断面面积;v=v(t,x)为通过过水断面的平均流速;g 为重力加速度;h=h(A)为相应断面面积A 的水深,h=h(A)适当光滑,且满足以下条件:
h'(A)>0,h"(A)>0,∀A>0;A0(x),v0(x)∈C1(R),且其C1模有界。
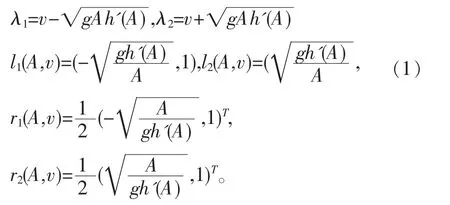
引进Riemann 不变量,
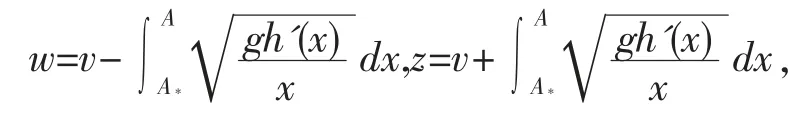
则方程组(1)可化为


对于式(2),假设:

1.2 主要定理
定理1:在假设(H1)、(H2)之下,若ε 充分小,则Cauchy 问题在t≥0 上存在整体经典解。
定理2:在假设(H1)之下,若ε 充分小,且∀x∈R,有(w0(x),z0(x))≥-3M 成立,则Cauchy 问题在t≥0 上存在整体经典解。 这里f 的定义分别见式(4)、式(5)和式(14)。
2 定理证明
2.1 定理1证明
为了证明定理1,先引入下面的引理。
引理1[7]:考虑如下拟线性双曲方程组的Cauchy问题。
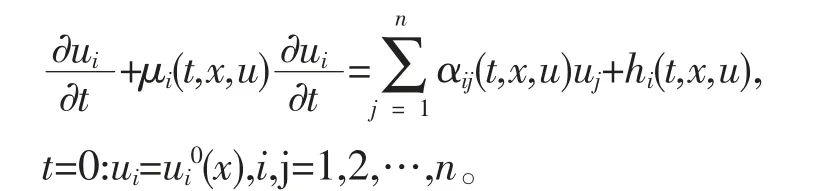
这里u=(u1,u2,…,un)T是关于t、x 的未知向量函数,μj、αij、hj(i,j=1,2,…,n)是其定义域 上的连续函数,并且μj关于t 有界,关于x,u 是局部Lipschitz 连续。 若u=u(t,x)是上述Cauchy 问题的一个C1解,则∀(t,x)∈R+×R 有下边的不等式成立:

由引理1,可得出如下推论。
推论1:在假设(H1)下,若ε 充分小,则在Cauchy 问题的经典解存在区域上有|v(t,x)|≤C1ε,0<A*-C2ε≤A(t,x)≤A*+C2ε。 对方程组(2)两端关于x求偏导得

经详细计算有
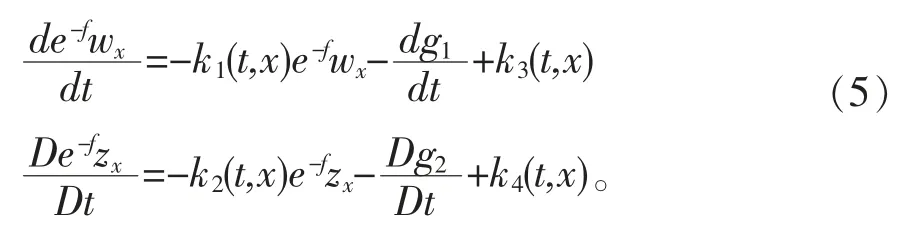
其中,
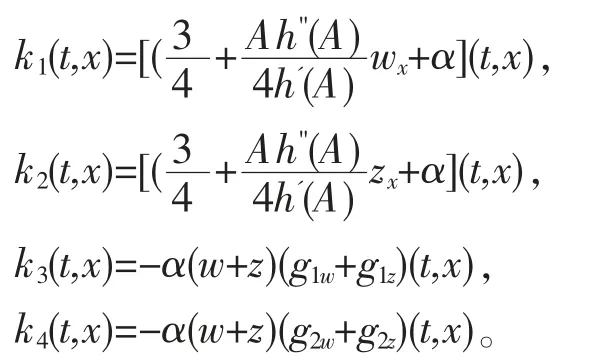
假设方程组(2)的第i 特征线为
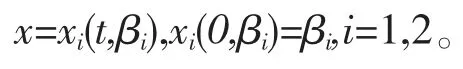
则由假设(H2)得:
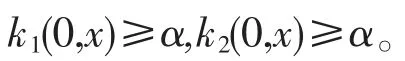
由推论1 和引进的Riemann 不变量可知,存在正常数M1,M2,使得:
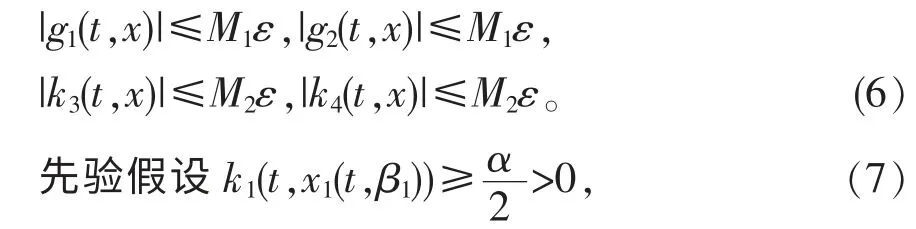
沿着第1 特征线积,并由式(5)~式(7)以及假设(H1)、(H2)易证

这里M3、M4是不依赖于ε 的正常数。
由推论1 知,存在充分小的ε0>0,使得当∀ε∈(0,ε0],先验假设式(7)是合理的。 由式(8)即得对∀ε∈(0,ε0],有
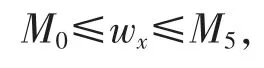
其中,M5(>0),M0是常数。
同理可证

即有

则由局部解存在性定理[8],定理1 得证。
如果
2.2 定理2 证明
令

则式(2)可以改写为

其中
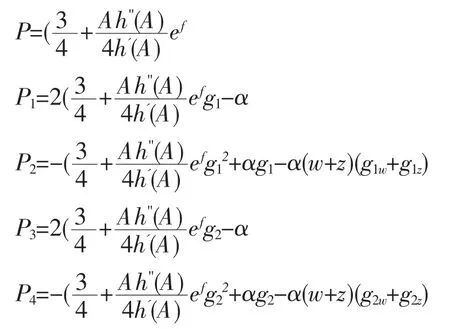
记
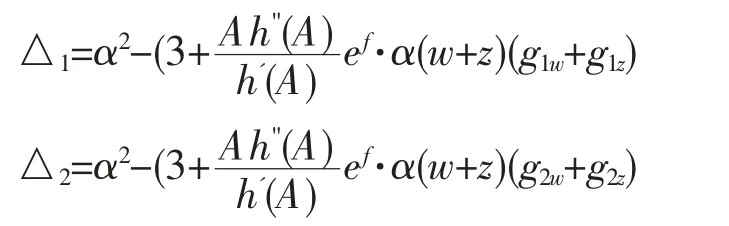
由P 及Pi(i=1,2,3,4)的定义和推论1 知,存在充分小的ε0>0,∀ε∈(0,ε0]有
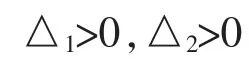
再令
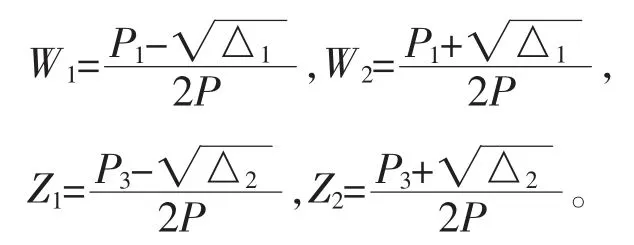
则式(10)可以改写为
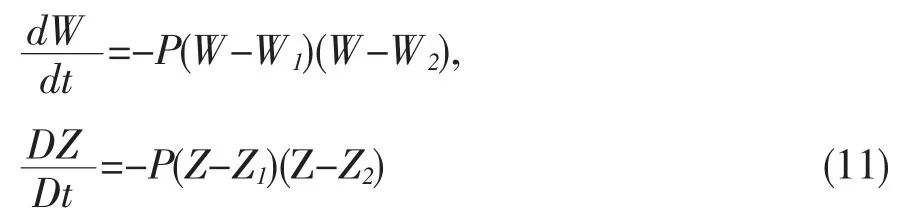
在Cauchy 问题的经典解存在区域上,定义

引理2[9]:考虑如下的初值问题
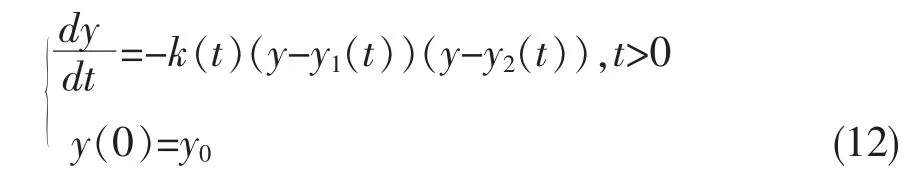
这里k(t)、y1(t)、y2(t)∈C0,(C0模有界),并且
那么对初值问题式(12),在其C0解的存在区域上有

那么初值问题式(12)的C0解y(t)必在有限时间内破裂,也就是存在一有限的T>0,使得
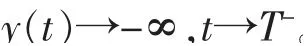
由引理2 可得引理3:考虑方程组(11)具有如下始值的Cauchy 问题
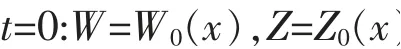
假设在Cauchy 问题的经典解存在区域上,||v(t,x)||和||A(t,x)||C0是有界的,且∀(t,x)∈R+×R,有σ1>0,σ2>0。 如果
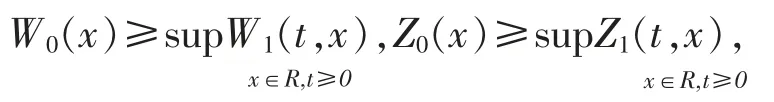
则在经典解存在区域上,有下式成立:
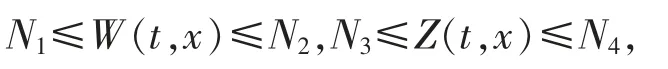
其中
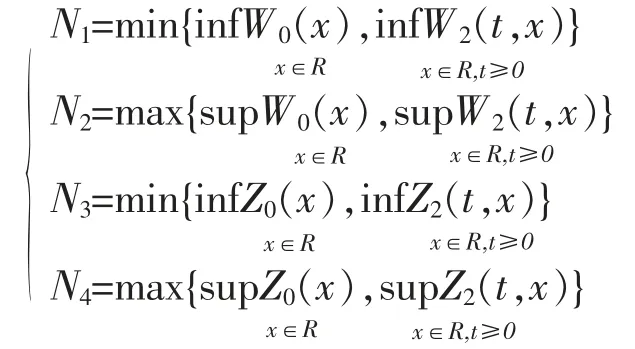
当ε→0+时,易知下式成立:
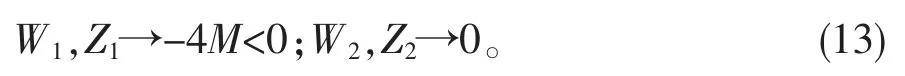
其中,

于是,存在充分小的ε>0,对∀ε∈(0,ε0],由式(9)、式(10)知:
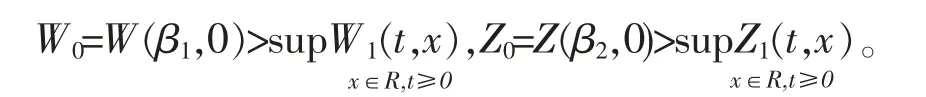
则由引理3 知,在式(10)光滑解的存在区域上有
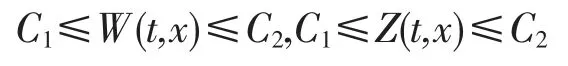
式中:C1,C2是不依赖于ε 的常数。 因此,当ε 充分小时,存在常数C,使得
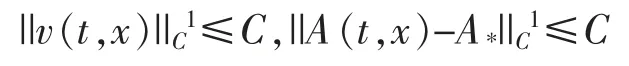
由局部解存在性定理[8],定理2 得证。
2.3 定理3证明
由定理2 的证明知,当ε0充分小时,W0=W(β1,或成立。 则由引理2 可知定理3 成立。
3 结语
由圣维南方程组的推导过程可以知道,摩阻力是由河槽底部及两侧的剪切力所造成的,可用明渠阻力经验公式(曼宁公式或谢才公式)来表示。 本文的结果表明,低阶耗散可以保证整体经典解的存在性,但耗散项对整体的影响比较小,而高阶耗散则不然。 本论文中解的破裂结果表明,具线性耗散摩阻力的流体,若初速度和对流加速度(v(x)v'(x))很小,而且过水断面保持基本不变,则水流会按照初始状态一直保持不变。 如果在某点过水断面突然发生改变,则流速也会随之改变,水流就会产生水跃(解发生破裂)。 由于耗散形式的摩阻力在实际河槽中表现为河底凹凸不平,河道两侧形状不规则,因此,在改造天然河流以及人工修建河道及其他水利工程时,河道的形状一定要尽量规则,底部应尽量平整。
[1] 章梓雄,董曾南.粘性流体力学[M].北京:清华大学出版社,1998:422-456.
[2] 赵克玉. 天然河道一维非恒定流数学模型[J].水资源与水工程学报,2004,15(1):38-41.
[3] 陈大宏,蓝霄峰,杨小亭.求解圣维南方程组的DORA 算法[J].武汉大学学报,2005(38):41-44
[4] 刘法贵,聂大勇.河渠非定常流动问题的数学研究[J].周口师范学院学报,2006,23(5):27-29.
[5] 李大潜. 河渠非定常流动的精确能控性[J].南通工学院学报,2002,1(2):1-5.
[6] 刘法贵,聂大勇,朱善迎. 具高阶耗散河渠非定常流动方程组Cauchy 问题[J]. 华北水利水电学院学报,2007,28(3):107-109.
[7] Zhao Yanchun. Global Smooth Solutions for One Dimensional [J]. Gas Dynamics Systems, Uinversint of Minnesta,IMA preprint 545, 1989:1-11.
[8] Li Tatsien, Yu Wenci. Boundary Value Problems for Quasilinear Hyperbolic Systems [M].Duke University Mathematics V, 1985:7-11.
[9] Liu Fagui. Cauchy Problem for Quasilinear Hyperbolic Systems[M].Yellow River Conservancy Press,2006:12-14.

