GPS/SINS紧组合导航系统信息融合技术研究*

吴凤柱，何 矞，焦 旭，李南海

（南昌航空大学 信息工程学院，江西 南昌 330063）

惯性导航是一种完全自主的导航系统，具有隐蔽性好、抗干扰、不受气象条件限制的优点。但其缺点是其定位误差随时间积累。全球定位系统具有全天候、高精度、定位误差不随时间发散等显著特点，但卫星信号可能被人为地添加干扰，而且受环境的限制，故可靠性较差。而GPS和SINS组合系统则取长补短，充分发挥各自的优势。基于伪距、伪距率组合的GPS/SINS紧组合导航系统和基于速度、位置组合的松组合系统具有精度更高、可靠性和抗干扰能力更强的优点。因此越来越广泛地应用于航空、航天领域。

1 紧组合导航系统的模型

基于伪距、伪距率的GPS/SINS紧组合导航系统是一种高水平的组合方式,其主要特点是GPS接收机和SINS相互辅助。它利用GPS的星历数据与SINS给出的位置和速度信息计算出相应的伪距和伪距率,然后与GPS接收的伪距和伪距率相比较得出的误差作为量测值,通过卡尔曼滤波器估计 GPS和SINS的误差量,从而实现系统的校正。在该组合模式中,GPS接收机只提供星历数据和伪距、伪距率即可,省去导航计算处理部分,有着精度高、鲁棒性好、抗干扰性强等特点。

1.1 紧组合导航系统的状态方程

GPS/SINS紧组合导航系统的状态方程由两部分组成，一个是SINS导航系统的状态方程，另一个是GPS导航系统的状态方程。GPS系统的误差状态通常取两个，一个是与时钟误差等效的测距误差δtu，另一个是与时钟频率误差等效的距离变化率误差δtru。

本文采用的导航坐标系为东北天地理坐标系，则SINS导航系统的误差状态方程表达式如下：

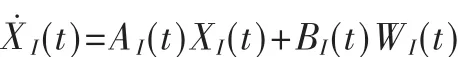
其中:XI=[φeφnφuδVeδVnδVuδL δλ δh εxεyεz▽x、 ▽y、▽z]T，φe、φn、φu为三个方向的平台误差角 ，δVe、δVn、δVu和 δL、δλ、δh 分别为三个方向的速度和位置误差，εx、εy、εz和▽x、▽y、▽z分别为陀螺仪和加速度计在三个方向的偏置误差。

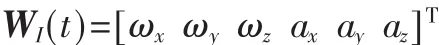
AI和BI的具体参数设置可见参考文献[1]。

GPS导航系统的误差状态方程可表达如下：

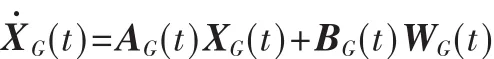
将以上SINS的误差状态方程与GPS的误差状态方程合并,可得到基于伪距、伪距率的紧组合导航系统的状态方程:

1.2 紧组合导航系统的量测方程

GPS/SINS紧组合导航系统量测方程包括伪距观测量组成的系统伪距量测方程和伪距率观测量组成的系统伪距率量测方程。

GPS/SINS紧组合导航系统的伪距量测方程如下：

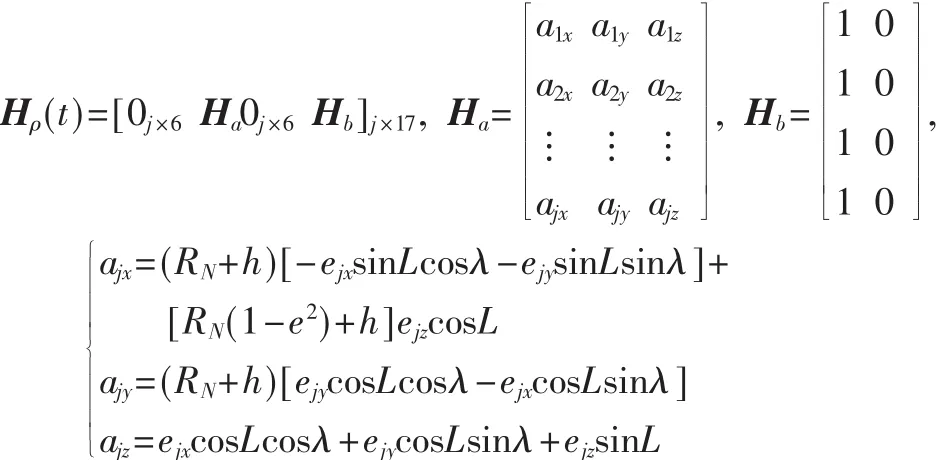
GPS/SINS紧组合导航系统的伪距率量测方程如下：

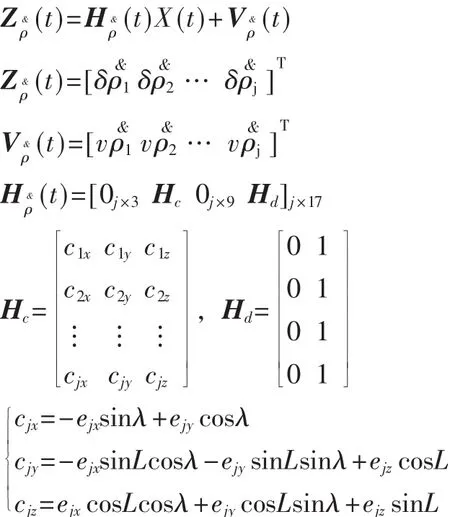
将伪距量测方程和伪距率量测方程合并，得到GPS/SINS紧组合导航系统量测方程：

1.3 紧组合导航系统方程的离散化

由于系统本身是连续的，将紧组合导航系统的状态方程(1)和量测方程(2)离散化可得：

式中:

2 紧组合导航系统的信息融合算法

2.1 EKF滤波算法

由于GPS/SINS紧组合导航系统的方程是非线性的，而对于非线性系统，通常传统的卡尔曼(KF)是不可取的。目前在组合导航中，EKF应用较为广泛。EKF对非线性系统的处理办法是将非线性系统线性化,然后对线性化后的系统采用标准卡尔曼滤波获得状态估计。

假设系统的状态空间方程为：

式中,X(k)为系统状态向量,Z(k)为系统的观测向量,系统噪声 W(k)和量测噪声 V(k)分别为协方差为 Q、R的高斯白噪声。

将方程(3)和(4)围绕滤波估计值进行Taylor级数展开并略去二次以上项,有:

上式中W(k)和V(k)是互不相关的白噪声序列,协方差分别为Q(k)和R(k)。设在时刻j得到的测量为{Z(1),Z(2),...,Z(j)},EKF滤波就是要通过这些测量值求得状态X(n)的最佳线性估计。再应用Kalman滤波基本方程可得滤波估计方程为：X^(k)=MX^(k-1)+K(k)[Z(k)-MNX^(k-1)]；滤波增益方程为：K(k)=P(k|k-1)NT[NP(k|k-1)NT+R(k)]-1，其中 P(k|k-1)=MP(k-1)MT+Q(k-1)；滤波协方差方程为：P(k)=P(k|k-1)-K(k)NP(k|k-1)。

2.2 UKF滤波算法

UKF是一种非线性滤波算法，该方法利用一系列近似高斯分布的采样点,通过UT变换来处理均值和协方差的非线性传递。

假设系统的状态方程和量测方程如式(1)和式(2)，则UKF算法的流程如下:

(1)初始状态向量X0及协方差矩阵P0,并给出系统噪声和量测噪声协方差阵Q和R。

(2)k＞1时，计算 2n+1个 sigma点

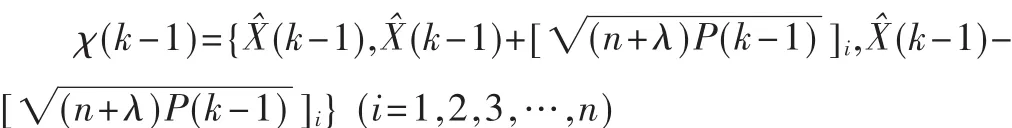
(3)时间更新

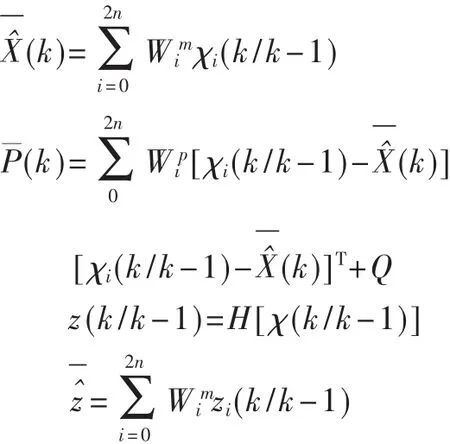
(4)测量更新

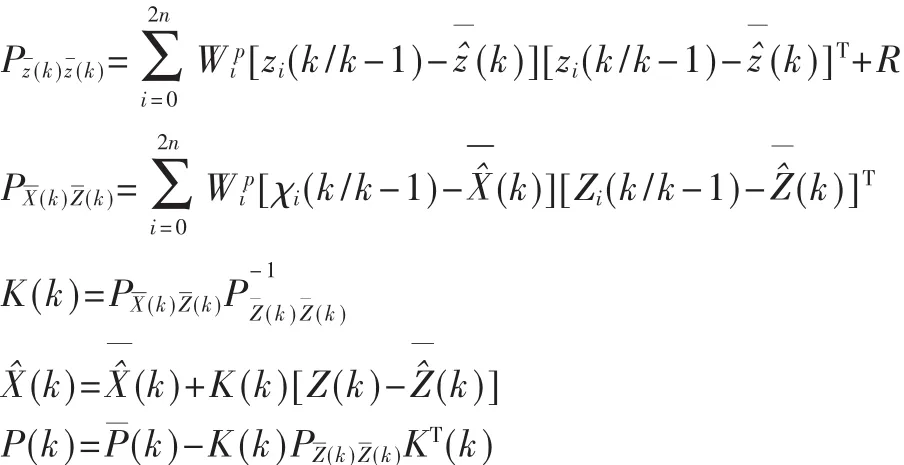
从EKF和UKF的计算过程可以看出，UKF具有以下优点：

(1)UKF直接利用非线性模型,避免引入线性化误差,从而提高了滤波精度；

(2)不必计算雅可比矩阵；

(3)能对所有高斯输入向量的非线性函数近似，均值精确到三阶，方差精确到二阶。

综上所述，UKF比较适合作为紧组合导航系统的信息融合算法。接下来将这两种滤波算法分别应用于紧组合导航系统中，通过比较来说明UKF相对于EKF的优越性。

3 系统仿真分析

下面在紧组合导航系统中应用EKF和UKF两种滤波方法对系统进行仿真，进而验证UKF优于EKF。

弹体运动轨迹参数设置如下:初始纬度32°,经度118°,高度 300 m，初始失准角为 15°，三个方向的初始速度误差分别为0.5 m、0.8 m和0 m，初始位置误差分别为10′、10′和 0，陀螺仪零偏为 0.1°/h，相关时间为 1 h，加速度计零偏为0.001 g,相关时间为0.5 h、GPS伪距误差为1 m,伪距率误差为0.05 m/s,仿真时间为4 000 s。仿真框图如图1所示。仿真结果如图2～图5所示。

通过仿真结果可以明显地看出，UKF在位置和速度的估计精度上优于EKF,且UKF的稳定性和收敛性也很好。

基于GPS/SINS紧组合导航系统较松组合导航系统有明显的优势。本文首先建立了紧组合导航系统的数学模型，然后将EKF和UKF滤波算法引入到紧组合导航系统中，最后通过对仿真结果进行比较，证实了仿真结果和理论分析的一致性，进而验证了UKF算法可以更好地处理非线性问题。由此可见，UKF是GPS/SINS紧组合导航系统中较适用的一种滤波算法。

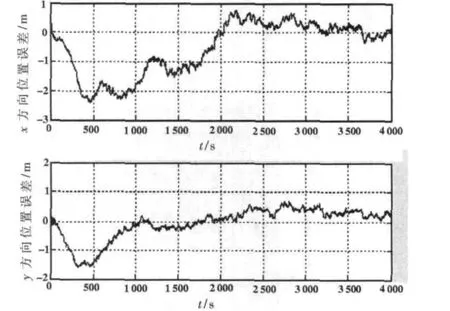
图4 UKF的位置误差曲线

图5 UKF的速度误差曲线

[1]王惠南.GPS导航原理与应用[M].北京：科学出版社，2010.

[2]周凤崎，卢晓东.最优估计理论[M].北京：高等教育出版社，2009.

[3]谢钢.GPS原理与接收机设计[M].北京:电子工业出版社,2009.

[4]袁俊刚.GPS/惯性紧组合导航系统研究[D].南京:南京航空航天大学,2011.

[5]田磊.GPS/INS组合导航中的非线性滤波方法研究[D].成都:电子科技大学,2010.

[6]周坤芳,吴晞,孔键.紧耦合 GPS/INS组合特性及其关键技术[J].中国惯性技术学报，2009,17(1):42-45.

[7]丁传炳,王良明,常思江.GPS/INS组合导航在制导火箭弹中的应用[J].火力与指挥控制,2010,35(17):138-141.