残差和为零的非线性回归在材积建模中的应用
王仲锋,周红梅
(长春工程学院勘查与测绘工程学院,长春130021)
在解决诸如幂函数、指数函数、双曲函数和S型曲线等非线性函数回归分析问题时,传统方法是通过换元化为线性函数,按一元线性回归和等权方式(俗称拟线性回归)求解被估计参数。如此做法将带来严重的异方差问题[1-4],致使回归参数无法使用。解决拟线性回归中异方差问题的有效方法是采用加权回归[2]和非线性最小二乘回归[3]。然而,加权回归和非线性最小二乘回归通常存在残差和不为零的问题。有些时候,建立回归方程的目的并不侧重于对个体进行预测,而是侧重于对总体进行预测。例如,在林业上建立木材材积模型时主要用于区域立木材积的估产。在此种情况下,对于非线性材积模型,用残差和为零的非线性最小二乘回归法进行数据处理,使模型的残差和为零将会提高区域立木材积估产的精度。
本文利用10个树种的建模(编表)数据、伯克霍特材积模型和山本和藏材积模型以及残差和为零的非线性回归分析法[1]进行木材材积建模,并用10个树种的验表数据对所建模型进行验证,同时和用非线性最小二乘回归法进行数据处理的结果进行比较,以验证残差和为零的非线性回归分析法的可行性和优越性。
1 残差和为零的非线性最小二乘回归[1]
1.1 非线性最小二乘回归
对于非线性样本回归方程组
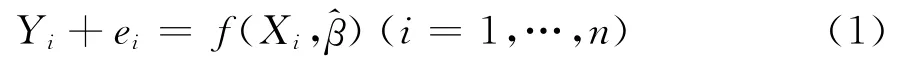
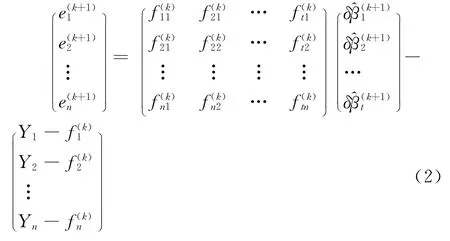
其中,
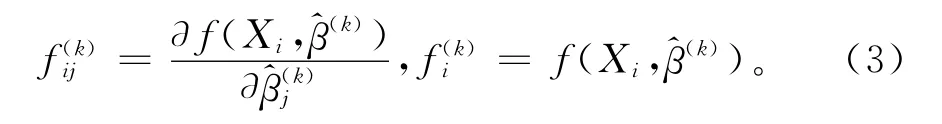
从左至右依次记式(2)中的矩阵为 e(k+1)、X(k)、和l(k),则式(2)可简写为
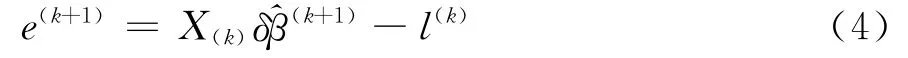
式(4)为线性化的误差方程,当Yi为等权(即ε~N(0,σ2I))观测值时,根据最小二乘原理,可得
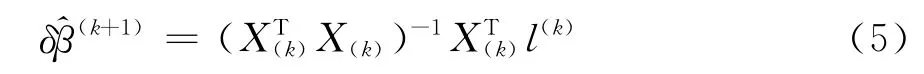
而

在不至于引起混淆的情况下,可把迭代结束后的式(4)简写为

显然,由于式(7)中X的第一列的元素通常情况下不全为1,故即使在等权观测情况下,非线性最小二乘回归的被解释变量观测值之改正数(回归的残差)ei的代数和亦不为零,也就是说非线性最小二乘回归通常是存在模型闭合差的。
1.2 残差和为零的非线性最小二乘回归
令
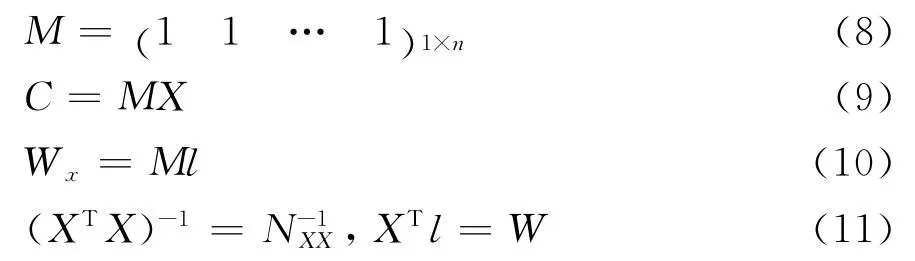
则可利用式(7)构建强制条件
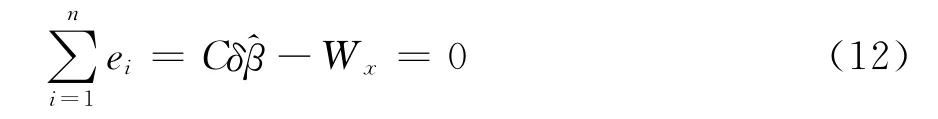
将式(7)与式(12)联立求解,根据附加限制条件的回归原理,可重新求得
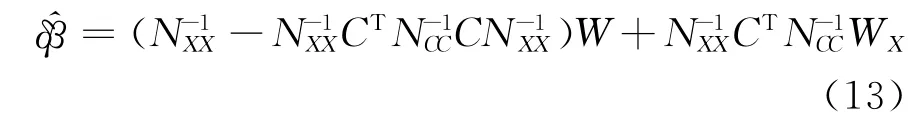

需要指出的是由于非线性回归后W =XTl=XT(Y-)=-XTe=0,故实际计算时式(13)变成

2 材积建模实验
2.1 实验的函数模型
实验共使用了一个一元材积模型和一个二元材积模型,其形式如表1所列。

表1 实验用的材积函数模型
2.2 实验数据
10个树种的编表与验表数据分别见表2和表3,数据来自吉林省和龙林业局。
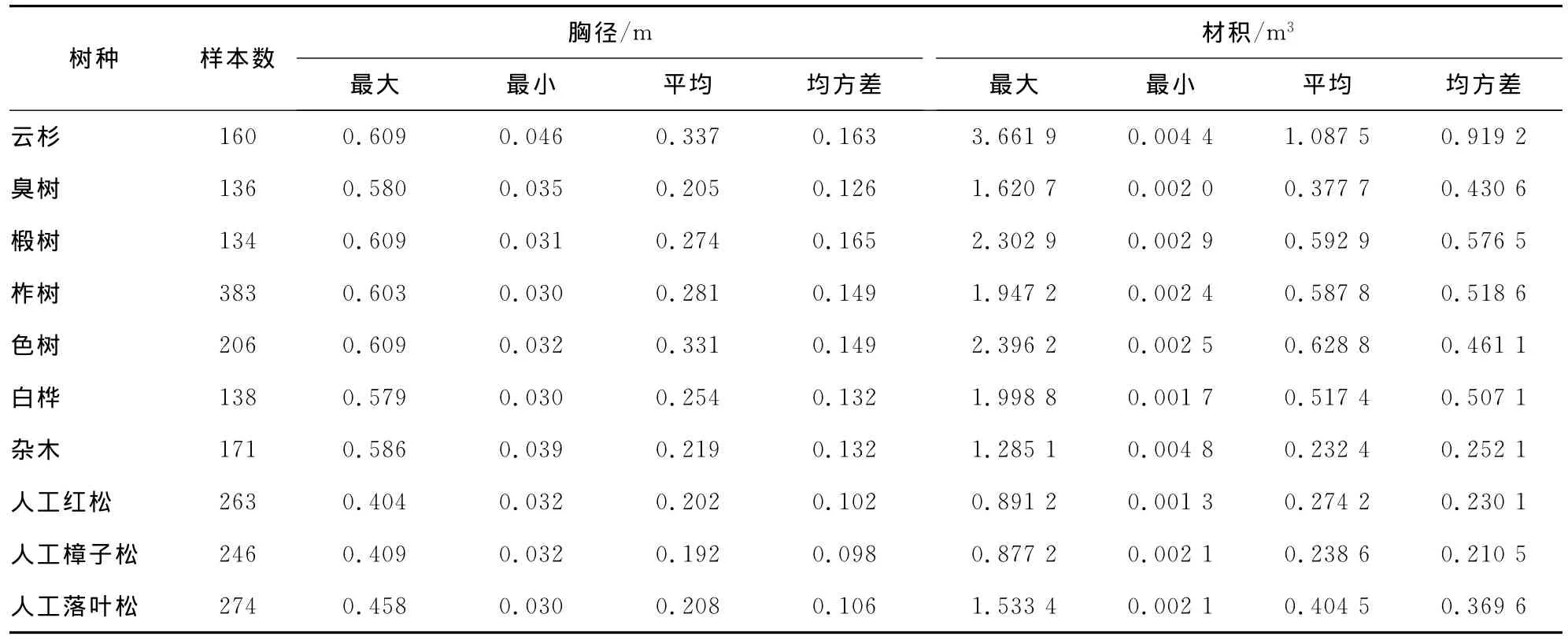
表2 10个树种的编表数据
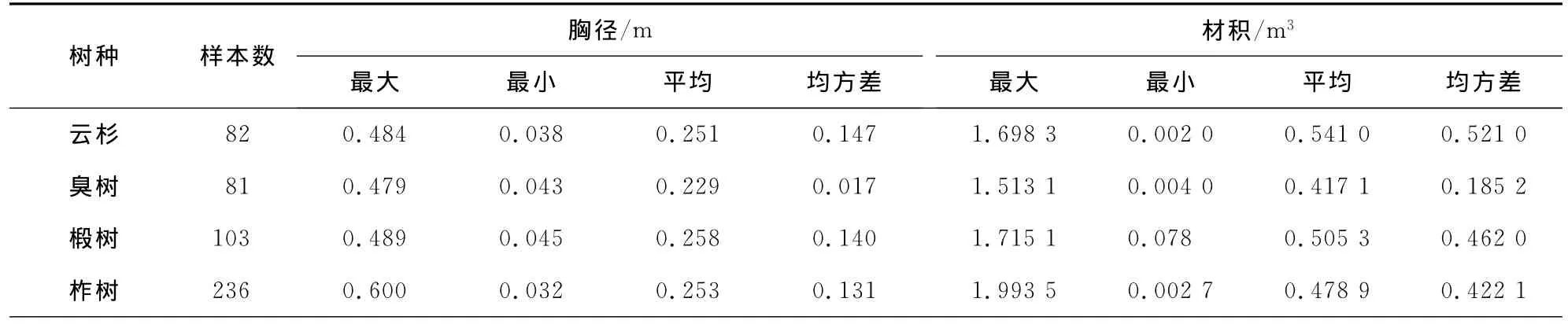
表3 10个树种的验表数据
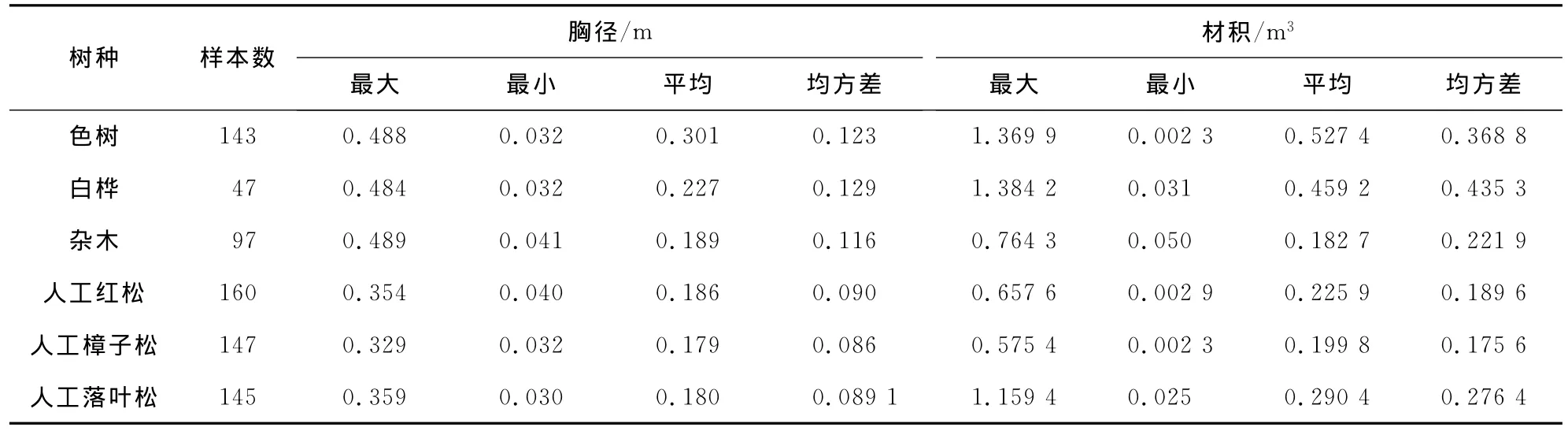
表3 (续)
2.3 建模闭合差
根据10个树种的编表数据、两个模型和两种方法求解的模型相对闭合差(残差和的绝对值/总材积)见表4。

表4 编表数据回归相对闭合差比较表/%
2.4 验表闭合差
用10个树种的验表数据队建立的模型进行检验,算得的相对闭合差见表5。

表5 验表相对闭合差比较表/%
2.5 实验分析
2.5.1 建模结果分析
由表4可知,两种数据处理方法建模时,非线性最小二乘回归建模的相对闭合差明显大于残差和为零的非线性回归建模的相对闭合差。10个树种采用伯克霍特材积模型和非线性最小二乘回归的相对闭合差在0.33%~4.46%之间,平均为1.55%,而采用残差和为零的非线性回归的相对闭合差在0.00%~0.07%之间,平均值为0.01%;10个树种采用山本和藏材积模型和非线性最小二乘回归的相对闭合差在0.02%~1.41%之间,平均值为0.61%,而采用残差和为零的非线性回归的相对闭合差在0.00%~0.06%之间,平均值为0.02%。两种材积模型及两种数据处理方法获得的10个树种的材积建模相对闭合差的比较见图1~2。
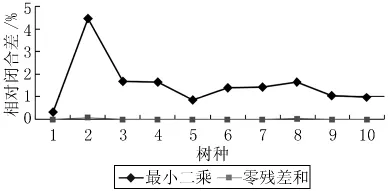
图1 伯克霍特材积模型建模的相对闭合差比较
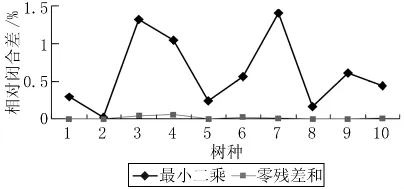
图2 三本和藏材积模型建模的相对闭合差比较
2.5.2 验表结果分析
(1)由表5知,由10个树种验表数据,采用伯克霍特材积模型和非线性最小二乘回归的参数求解的材积相对闭合差在0.99%~12.82%之间,平均为4.30%,而采用残差和为零的非线性回归的相对闭合差在0.00%~13.37%之间,平均值为3.01%;采用山本和藏材积模型时,由非线性最小二乘回归的参数求解的验表材积相对闭合差在0.10%~6.97%之间,平均为1.83%,而采用残差和为零的非线性回归的参数求解的验表材积相对闭合差在0.00%~7.44%之间,平均值为1.43%。两种材积模型及两种数据处理方法获得的10个树种的材积验表相对闭合差的比较见图3~4。
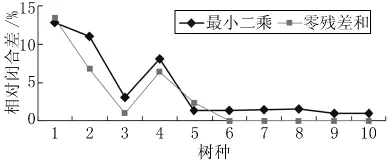
图3 伯克霍特材积模型验表的相对闭合差比较
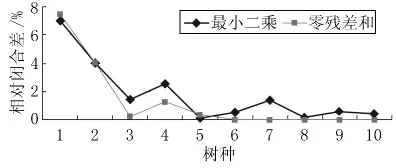
图4 三本和藏材积模型验表的相对闭合差比较
(2)无论采用伯克霍特材积模型还是山本和藏材积模型,其中8个树种用残差和为零的非线性回归方法获得的验表材积相对闭合差小于用非线性最小二乘回归方法获得的验表材积相对闭合差,只有两个树种(云杉、色树)的验表材积相对闭合差是前一种方法的结果略大于后一种方法的结果。
3 结语
无论伯克霍特材积模型还是山本和藏材积模型,当用残差和为零的非线性回归方法求解模型参数时,无论参数的精度(限于篇幅文中未列出)还是材积估算的精度(以相对闭合差为指标)均总体高于用非线性最小二乘回归方法求解模型参数时的参数精度和材积估算的精度。因此,残差和为零的非线性回归方法是适用于材积建模的一种较好的数据处理方法。
[1]王仲锋,王琦.残差和为零的非线性回归法及其应用[J].东北林业大学学报,2011(2):125-127.
[2]王仲锋.加权线性回归及其应用[J].长春工程学院学报:自然科学版,2010(3):118-121.
[3]王仲锋,冯仲科.林木生物量参数的非线性最小二乘解法研究[J].吉林农业大学学报,2006(3):261-264.
[4]王仲锋,冯仲科.几种一元拟线性回归中的问题与改进措施[J].东北师大学报:自然科学版,2006(4):45-52.

