基于伴随向量系的自由振动系统的动力响应分析

刘国松，刘 莹

（长春工程学院理学院，长春130012）

0 引言

非对称性对系统的影响之一是仅使用右模态已不能满足需要，其内部的正交性已经退化，因此必须引入左模态［1］。而重复频率现象对系统的影响是左、右模态的正交性也存在退化。这是因为若频率发生重复，则这些左、右状态向量不再能保证正交性。可以证明不同特征值所对应的左、右状态向量之间仍然是正交的［2］，但对于重频所对应的那些左、右状态向量却无法证明它们存在正交性［3］，此时施密特正交化技术的应用也存在困难。这是因为相对于对称重频系统来说，因为重特征值所对应的所有特征向量满足的是同一特征方程［4］，根据酉空间理论实施正交化后是满足原特征方程的，仍然为该重特征值的特征向量，但对于非对称重频系统左、右状态向量所满足的特征方程已不同，如何进行正交化策略还有待进一步研究。本文指出这种情况下，需摒弃左状态向量，直接引入右状态向量的伴随向量，将二阶非对称系统的运动微分方程转入状态空间中，将状态方程化为系列的一阶线性微分方程，在每一维坐标下进行动力响应分析。本文方法不仅适用于单频系统，也适合于重频系统，不仅适用于对称系统，也适用于非对称系统。

1 基本理论

对自由度为n的阻尼系统，设M、C、K分别是对称或非对称的质量、阻尼和刚度矩阵，相应的运动微分方程为

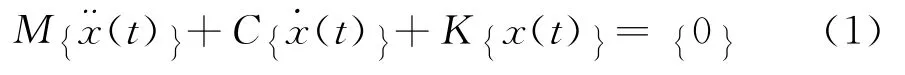
对此有阻尼振动系统，为了讨论其特征问题，引入状态方程［5］。对线性振动系统的运动方程式（1），设

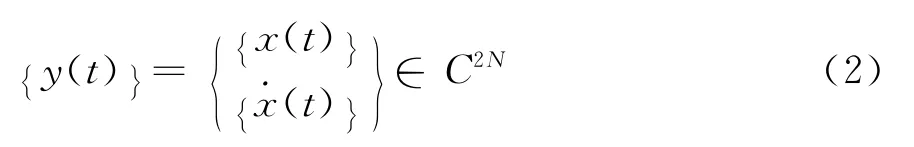
代入方程（1），则该二阶系统将转化为如下一阶系统：

其中

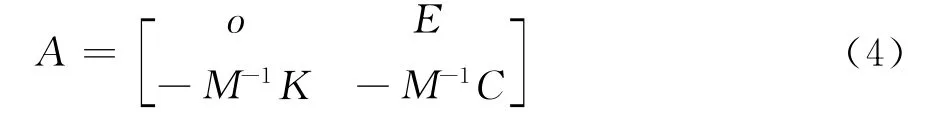
称为系统的状态矩阵。对一般动力系统（1），把时间域上的矩阵方程变换到以λ为变量的拉氏域中，并假定初始位移和初始速度均为零，其特征方程为

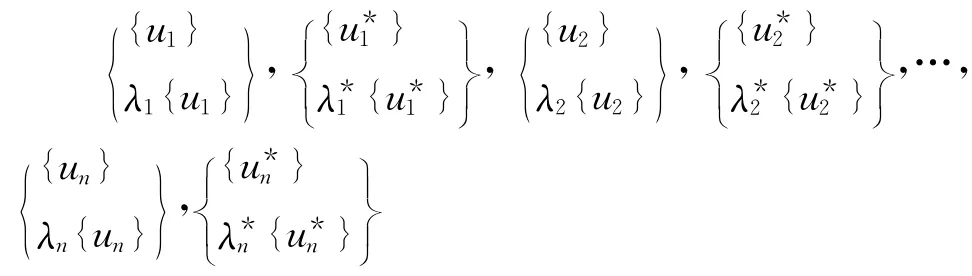
下文记为

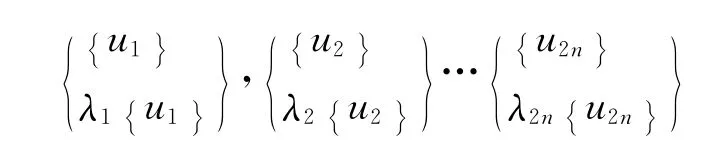
并满足方程

状态向量的前n维即为系统（1）的模态振型｛ui｝，即特征对（λi，ui）满足方程

2 基于伴随向量系的自由振动系统的动力响应分析

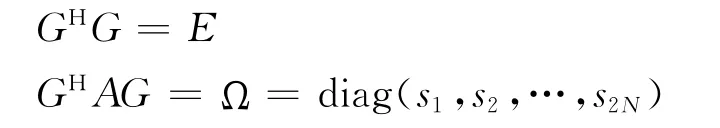
其中（·）H为（·）的共轭转置。对于完备重频系统，重频所对应的状态向量之间不存在足够的双正交性［2］。但无论上述两种情况的哪一种，2n个状态向量｛g1｝，｛g2｝，…，｛g2n｝的线性无关性是必定存在的，因此G可逆，故引入状态向量的伴随向量系Ψ＝［｛ψ1｝，｛ψ2｝，…，｛ψ2n｝］，它们可以满足良好规范正交关系

对方程（1）建立的状态方程

引入坐标变换

其中 ｛q（t）｝为模态坐标向量，代入状态方程（9）并左乘ΨH，根据左、右状态向量的正交性关系（7）和式（8），则有

展开写成

其中｛·｝i代表向量｛·｝的第i维。由此式（12）可表达为

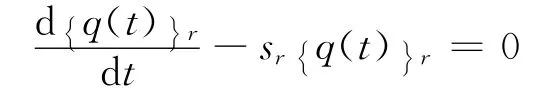
这是一个可分离的微分方程，即

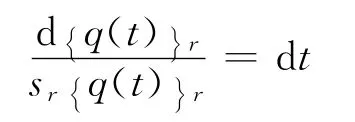
两边积分为

整理得

任意常数C由初值条件决定。解得 ｛q（t）｝，然后代入式（10）解得 ｛y（t）｝，由式（2）可知取前n维即为自由振动响应。

［1］Adhikari S，Friswell M I.Eigenderivative analysis of asymmetric non－conservative systems［J］.International－Journal for Numerical Methods in Engineering，2001，51：709－733.

［2］李德葆，陆秋海.实验模态分析及其应用［M］.北京：科学出版社，2001：10－11.

［3］Ward H，Stefan L，Paul S.Modal Analysis Theory and Testing［M］.Brussel，Belgium：Katholieke Universiteit Levven，1997：18－19.

［4］Li L，Yu J H，Xue L W.A parallel way for computing eigenvector sensitivity of asymmetric damped systems with distinct and repeated eigenvalues［J］.Mechanical Systems and Signal Processing，2012，30：61－77.

［5］Greco A，Santini A.Comparative study on dynamic analysis of non－classically damped linear system［J］.Structural Engineering and Mechanics，2002，14（6）：679－698.