S-修正的自适应卡尔曼滤波与模糊卡尔曼滤波相结合的汽车状态估计算法

黄 超 林 棻

南京航空航天大学，南京，210016

0 引言

准确而实时地获取汽车行驶过程中的状态信息是汽车动态控制系统研究的关键，由此衍生出的汽车状态估计器的设计逐渐成为近年来研究的热点。目前汽车状态估计器设计所采用的方法主要有线性卡尔曼滤波（Kalman filter，KF）、扩展卡尔曼滤波［1-3］、Unscented卡尔曼滤波［4-5］、神经网络［6］、状态观测器［7］、模糊逻辑［8］等，这些方法都是对汽车控制系统中的关键控制变量（包括质心侧偏角、侧向速度、横摆角速度等）进行估计。

上述算法中广泛应用的是基于KF的改进算法，而在常规KF算法中，量测噪声的统计特性在滤波过程中预先设为定值，若噪声水平改变，将会使得估计精度降低甚至导致滤波发散。为了提高基于KF汽车状态估计算法的鲁棒性与估计精度，本文提出一种改进的自适应模糊卡尔曼滤波算法，该算法是S-修正的自适应卡尔曼滤波（以下简称S-AKF）算法与模糊卡尔曼滤波（FKF）算法的结合，其中的S-AKF算法基于数学理论推导直接对估计误差协方差矩阵进行加权处理，而模糊卡尔曼滤波基于模糊逻辑推理，根据实时得到的量测信息的实际方差与理论方差的比值，由设计的模糊系统在线实时调整量测噪声矩阵。这使滤波算法不需要得到准确的量测噪声矩阵的先验知识，且对于时变的量测噪声也能得到准确的估计值。

由于FKF算法是对量测噪声的协方差矩阵进行自适应估计，状态量的估计精度会受到不准确的过程噪声的统计特性影响，而S-AKF恰可以弥补这个缺陷，故本文将S-AKF与FKF相结合，可以在很大程度上提高算法的估计精度及鲁棒性。

1 汽车动力学模型

仅考虑汽车沿y轴的侧向运动与绕z轴的横摆运动这两个自由度，另外限定汽车的侧向加速度在0.4g以下，轮胎侧偏特性处于线性范围，因此建立线性二自由度汽车模型如图1所示，模型描述［9］如下：

式中，m为整车质量；Iz为整车对z轴转动惯量；a为质心到前轴的距离；b为质心到后轴的距离；k1为前轮侧偏刚度；k2为后轮侧偏刚度；vx为质心处纵向速度；vy为质心处侧向速度；δ为前轮转角；ax为纵向加速度；ay为侧向加速度；β为质心侧偏角；ωr为横摆角速度。

由运动学的基本关系并结合图1，可得tanβ＝vy／vx，由于β 较小，则可得

将式（1）～ 式（4）整理后得状态方程和观测方程如下：

图1 汽车二自由度模型示意图

2 S-AKF算法

对于线性常规Kalman滤波算法，系统的状态空间模型为

式中，Xk为状态向量；Φk／k-1为状态转移矩阵；Hk为量测矩阵；Zk为观测向量；W、V分别为过程噪声向量和量测噪声向量。

滤波的预测与更新过程如下：

状态预测公式为

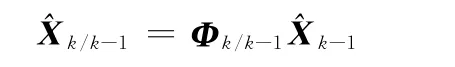
方差预测公式为

滤波增益公式为

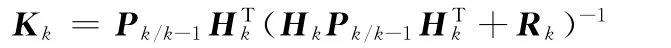
方差更新公式为

状态更新公式为

式中，P为误差协方差矩阵；Q、R分别为过程噪声协方差矩阵和量测噪声协方差矩阵；K为滤波增益矩阵；I为单位矩阵。

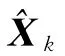
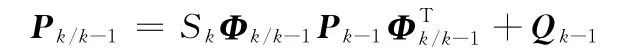
Sk值的选择过程如下：

判断滤波发散性的条件是

又有

最后可得

具体的推导过程参考文献［10］。

3 FKF算法及整体程序流程

常规KF算法假定观测噪声为零均值的高斯白噪声，且已知方差阵R。对于汽车行驶的实际过程，观测噪声的统计特性是不确定的，它易受外界环境的影响，通过引入模糊控制器可以在线估计R值［11］。定义k时刻观测噪声方差的估计值为＾Rk，且有

式中，α为自适应调整因子。

定义k时刻信息的实际方差与理论方差的比值为

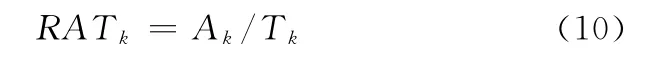
式中，Ak为新息的实际方差；Tk为新息的理论方差。

3.1 模糊规则的设计

本文中模糊控制器以信息的实际方差与理论方差的比值为输入，以自适应调整因子α为输出。最优情况下，信息的理论方差应近似等于实际方差值，如果理论方差长期偏离实际方差，说明观测噪声统计特性发生了变化，需要对理论方差进行调整，以使其回到实际方差附近。根据上述思想，设计模糊控制器。上述设计过程借助MATLAB中的FUZZY工具箱完成，然后利用Simulink模糊控制器将上述模糊工具箱封装起来，形成Fuzzy＿R模糊控制器，基本步骤如图2所示。

图2 Fuzzy＿R模糊控制器

定义输入输出的模糊子集如下：L1表示小于1，E1表示约等于1，M1表示大于1。本文采用的输入输出隶属度函数为三角形隶属度函数，具体如图3和图4所示。

模糊逻辑规则如下：

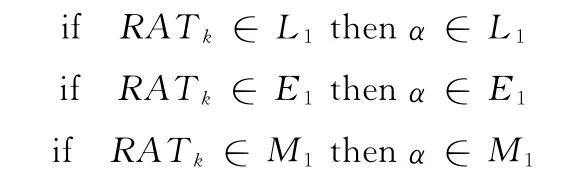
解模糊化方法有最大隶属度法、重心法、加权平均法等，本文采用目前应用较多的重心法进行求解。

图3 输入的隶属度函数

图4 输出的隶属度函数

3.2 M文件与Simulink混合编程流程

Simulink是基于MATLAB的框图式仿真环境，具有结构清晰、建模迅速等优势，但实现循环等操作复杂，执行效率低；M文件编程环境代码执行效率高，但程序结构复杂，建模较困难。本文结合两者的优势，程序主体结构采用M文件来编写，模糊控制器采用Simulink框图来搭建，并供主程序调用。从图5可看出，滤波循环过程在KF的基础上依次顺序加入了式（8）以及图2的Fuzzy＿R模糊控制器，这样在每一次循环中都可以利用FKF对量测噪声协方差矩阵进行在线估计，并利用S-AKF对估计误差协方差矩阵直接加权，给滤波过程加入了“双保险”，使得算法更加有效。

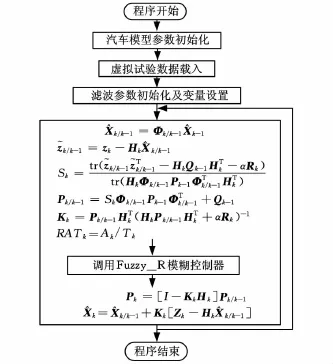
图5 程序流程框图

4 虚拟试验验证

为了检验算法的正确性，在虚拟样机软件ADAMS／CAR中建立整车模型，为了模拟极限工况下的汽车操纵响应，在仿真中采用驱动样机产生汽车的行驶路径，如图6所示。进行双移线工况仿真，整车的参数如下：m＝1528kg；Iz＝2440kg· m2；a ＝ 1.48m；b ＝ 1.08m；k1＝-226180N／rad；k2＝-294 390N／rad；试验车速为80km／h，整个过程历时10s；Qk＝I3×3，R0＝1。为充分检验算法的鲁棒性与估计精度，给观测量ay加入时变的高斯白噪声，如图7所示，具体如表1所示。

图6 汽车的行驶路径

图7 带有时变噪声的侧向加速度

表1 量测值时变噪声方差值

从图8、图9可以看出，由于噪声时变的影响，使得横摆角速度与质心侧偏角的估计值偏离虚拟试验值，估计误差增大。

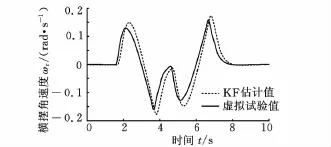
图8 未加入自适应算法的横摆角速度估计值

图9 未加入自适应算法的质心侧偏角估计值

综合图10、图11可以看出，单纯采用FKF算法时，质心侧偏角的估计值可以平稳地跟踪虚拟试验值的结果，但横摆角速度的估计值仍然出现一定的误差。这是因为状态量的估计精度不仅与量测噪声有关，而且还与过程噪声有关，且仿真中将Qk设为定值，不准确的过程噪声协方差矩阵导致了横摆角速度的估计误差。

图10 不同自适应算法的横摆角速度估计值

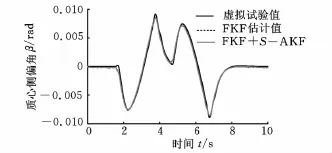
图11 不同自适应算法的质心侧偏角估计值

当算法中加入S-AKF之后，FKF＋SAKF算法的估计结果较之前的算法有了很大改善，横摆角速度与质心侧偏角的估计值均能较好地跟踪虚拟试验值的结果，说明S-AKF的加入可以弥补FKF算法的不足，从而可以获得更高的鲁棒性与估计精度。

基于个人电脑和MATLAB环境的程序累积运算时间为8.9s。在时间历程为10s的虚拟试验下具有较好的实时性。

为了定量的比较两种算法的估计精度，给出了估计值相对于实际值的平均绝对误差（MAE）和均方根误差（RSME），如表2、表3所示。

表3 3种算法的RSME指标

从表2和表3可以看出，随着算法的改进，横摆角速度的MAE和RSME指标明显逐步变好；质心侧偏角的MAE和RSME指标呈现下降趋势，虽然FKF＋S-AKF指标相对于FKF时略微反弹，但差别不大。从算法的总体效果来看，FKF＋S-AKF算法优于其他的算法。

3.1 节中设计的模糊控制器对滤波过程中的每一次递推循环均进行噪声协方差的自适应调整，与表1进行对应可得具体的调整效果，如图12所示。

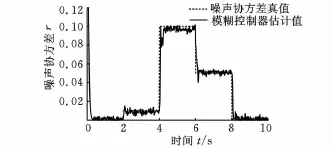
图12 量测噪声协方差真实值与估计值

从图12可以看出，模糊控制器可以较好地跟踪量测噪声协方差矩阵的变化，所以本文的算法要比非自适应算法具有更高的估计精度。

5 结论

（1）提出将S-AKF与FKF相结合的汽车状态估计算法，FKF可以对时变噪声的协方差矩阵进行在线估计，实现其自适应；S-AKF算法是一种实际不发散的滤波算法，有较好的滤波精度，FKF＋S-AKF算法进一步提高算法的鲁棒性与估计精度。

（2）通过虚拟试验验证表明，FKF＋S-AKF算法的估计结果可以很好地跟踪虚拟试验值，因而优于其他算法。

（3）后续研究将致力于选择更优的模糊控制器，并应用到非线性汽车模型中，为汽车稳定性控制系统的研究提供理论指导。

［1］林棻，赵又群.基于双重扩展自适应卡尔曼滤波的汽车状态和参数估计［J］.中国机械工程，2009，20（6）：750-755.Lin Fen，Zhao Youqun.Vehicle State and Parameter Estimation Based on Dual Extended Adaptive Kalman Filter［J］.China Mechanical Engineering，2009，20（6）：750-755.

［2］郭孔辉，付皓，丁海涛.基于扩展卡尔曼滤波的汽车质心侧偏角估计［J］.汽车技术，2009（4）：1-3.Guo Konghui，Fu Hao，Ding Haitao.Estimation of CG Sideslip Angle Based on Extended Kalman Filter［J］.Automobile Technology，2009（4）：1-3.

［3］Chen B C，Hsieh F C.Sideslip Angle Estimation Using Extended Kalman Filter［J］.Vehicle System Dynamics，2008，46，353-364.

［4］赵又群，林棻.基于UKF算法的汽车状态估计［J］.中国机械工程，2010，21（5）：615-619.Zhao Youqun，Lin Fen.Vehicle State Estimation Based on Unscented Kalman Filter Algorithm［J］.China Mechanical Engineering，2010，21（5）：615-619.

［5］Antonov S，Fehn A，Kugi A.Unscented Kalman Filter for Vehicle State Estimation［J］.Vehicle System Dynamics，2011，49（9）：1497-1520.

［6］Melzi S，Sabbioni E.On the Vehicle Sideslip Angle Estimation through Neural Networks：Numerical and Experimental Results［J］.Mechanical Systems and Signal Processing，2011，25（6）：2005-2019.

［7］Cheli F，Melzi S，Sabbioni E.An Adaptive Observer for Sideslip Angle Estimation：Comparison with Experimental Results［C］／／ASME Conference Proceedings.Las Vegas，2007：1193-1199.

［8］施树明，Lupker H，Bremmer P，等.基于模糊逻辑的车辆侧偏角估计方法［J］.汽车工程，2005（4）：426-430.Shi Shuming，Lupker H，Bremmer P，et al.Estimation of Vehicle Side Slip Angle Based on Fuzzy Logic［J］.Automotive Engineering，2005，27（4）：426-430.

［9］余志生.汽车理论［M］.北京：机械工业出版社，2009.

［10］宋文尧，张牙.卡尔曼滤波［M］.北京：科学出版社，1991.

［11］肖志涛，赵培培，李士心.基于INS／GPS组合导航的自适应模糊卡尔曼滤波［J］.中国惯性技术学报，2010（2）：195-198.Xiao Zhitao，Zhao Peipei，Li Shixin.Adaptive Fuzzy Kalman Filter Based on INS／GPS Integrated Navigation System ［J］.Journal of Chinese Inertial Technology，2010（2）：195-198.