3×3光纤耦合器解调方法

张晓峻，康 崇，孙晶华

(哈尔滨工程大学理学院，黑龙江哈尔滨 150001)

1 引 言

光纤耦合器是一种使光信号在特殊结构的耦合区内发生耦合，将功率再分配的无源器件。它在光纤传感和光通信等领域有着广泛的应用，在耦合过程中，光信号的频谱成分不变，只是信号的光功率发生变化。1980年，K.P.Koo等［1］对3×3耦合器原理进行了理论分析，提出利用3×3耦合器实现干涉型光纤传感器的信号解调，建立了马赫-泽德尔型光纤干涉仪的模型。1981年，S.K.Sheem［2］第一次提出了用3×3耦合器构造光纤干涉仪来提高系统的灵敏度，它在结构上与Mach-Zehnder干涉仪类似，而把Mach-Zehnder干涉仪输出端的2×2耦合器由3×3耦合器取代。后来研究者对其结构进行不断的改进，提出了基于Michelson干涉仪的对偏振不敏感的构造。基于3×3耦合器的解调方法是一种无零差的解调方法，属于被动相位调制型［3-7］。以3×3耦合器为基础的干涉仪可实现干涉式光纤传感器、光纤光栅传感器以及光纤激光传感器的信号解调。它的特点是测量范围大，便于判断方向，灵敏度高，易于全光纤化等［8-9］。近年来，人们利用反馈光纤连接3×3耦合器的一对输入输出端口，通过改变反馈光纤的长度实现分束比的调节，来构造自己需要的光路结构和特殊器件。它具有体积小、重量轻、结构简单、性能稳定可靠、不需要调制光源，允许光路设计上的对称性偏差等优点。人们逐渐重视它在光纤水听器、光纤加速度计、光纤陀螺等光纤传感领域的应用［10-11］。采取高集成、并行处理SOPC技术，可实现解调系统的数字化［12］。

本文推导出了3×3光纤耦合器输出解调信号的数学表达式，给出了3×3光纤耦合器输出解调算法的解调频率范围，分析了外界干扰信号、耦合器的不对称性、以及信号中的高次谐波对解调结果的影响。

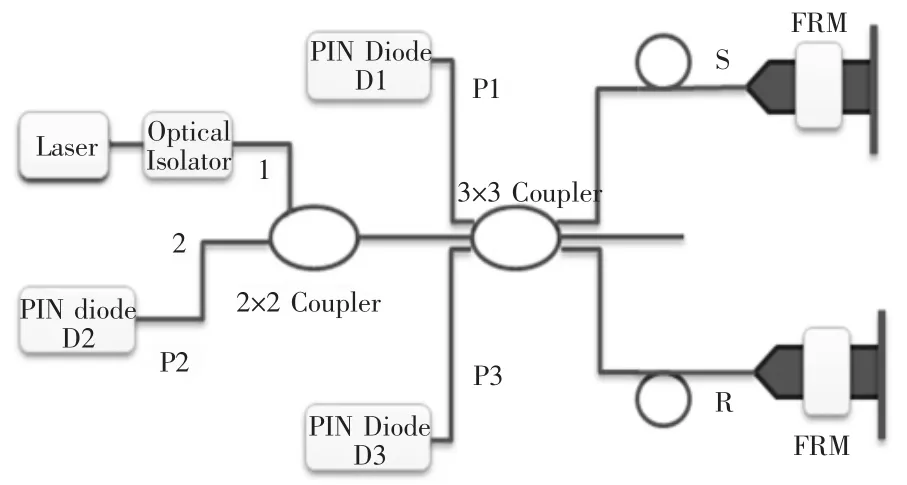
图1 基于3×3耦合器的干涉仪结构Fig.1 Probe interferometer structure diagram based on 3 ×3 coupler

2 3×3耦合器解调方法原理

基于3×3耦合器干涉仪的结构如图1所示。其中，2×2耦合器只是一个功率分配器，3×3耦合器3个输出量在相位上相差120°。S和R为3×3耦合器的两个臂，分别代表干涉仪的传感臂与参考臂。3个检测器分别检测3×3耦合器的3个输出信号，经电路处理，再经过运算，把需要的待测信号解调出来。

干涉仪的输出光强:

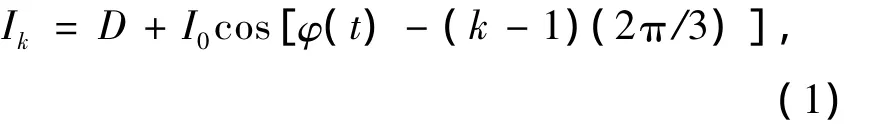
式中，φ(t)=φ(t)+ψ(t);D为输出光强的平均值;I0为干涉条纹的峰值强度;k为输出的光路序号，k=1，2，3;φ(t)为传感器相位差信号，即待测信号;ψ(t)为环境变化产生的相位差。

3×3耦合器的解调方法如图2所示。在图中，A1、A2、A3、A4、A5、A6、A7分别是相应 3 个加法器、微分器、乘法器、平方器与除法器的增益。φ(t)是解调过程的最后输出量。为推导方便，令:

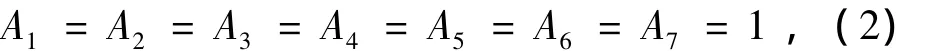
图2中将3路输出信号 I1、I2、I3相加，再乘以－1/3，得到第一个加法器的输出:

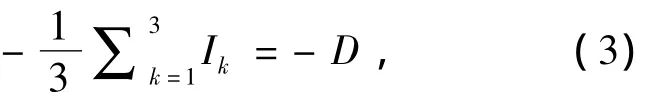
I1、I2、I3分别与 －D 相加得:

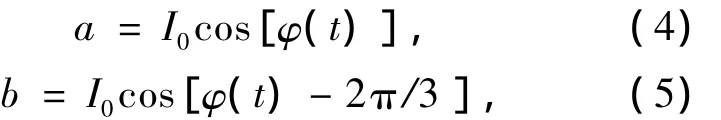
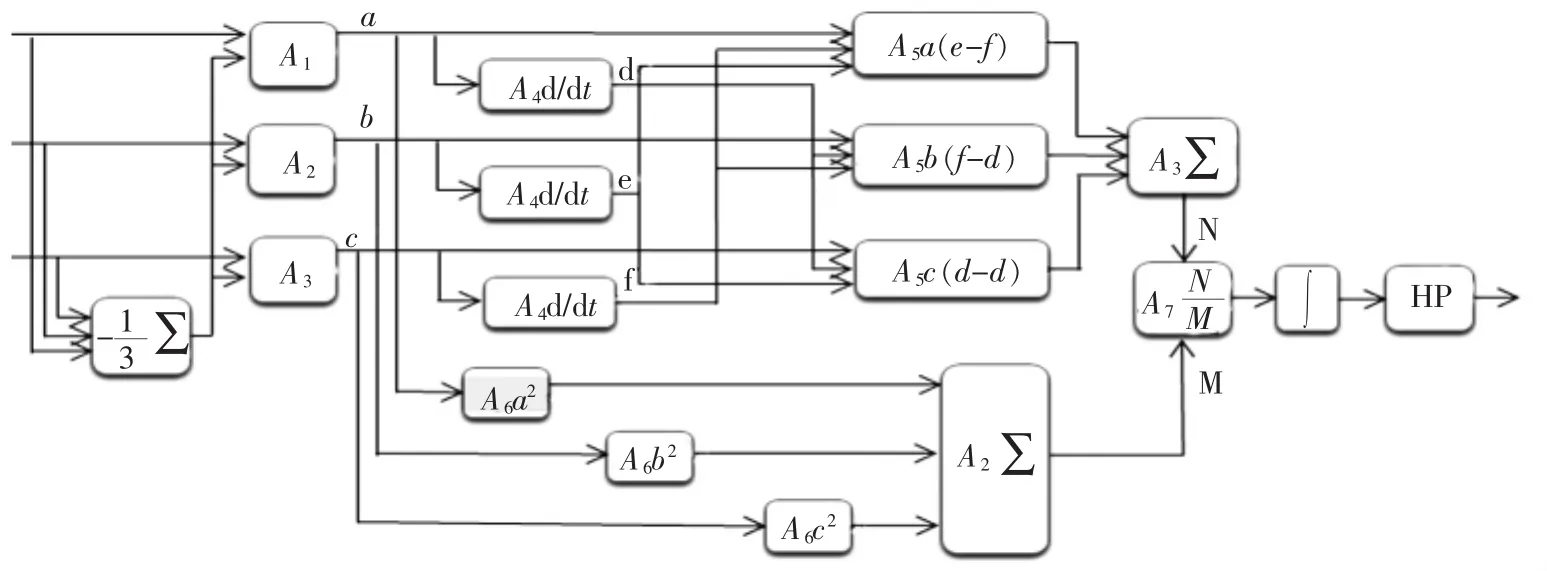
图2 基于3×3耦合器的解调方法Fig.2 Demodulation system based on 3 ×3 coupler

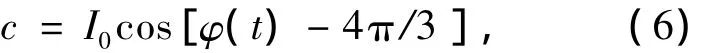
将a，b，c经过3个相同的微分器，微分可得:

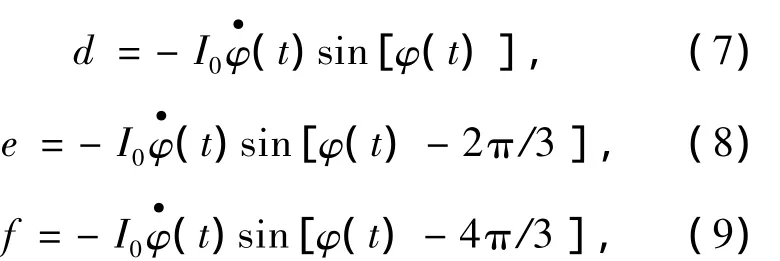
再将每一路信号a、b、c与另外两路微分后的差相乘，可得:

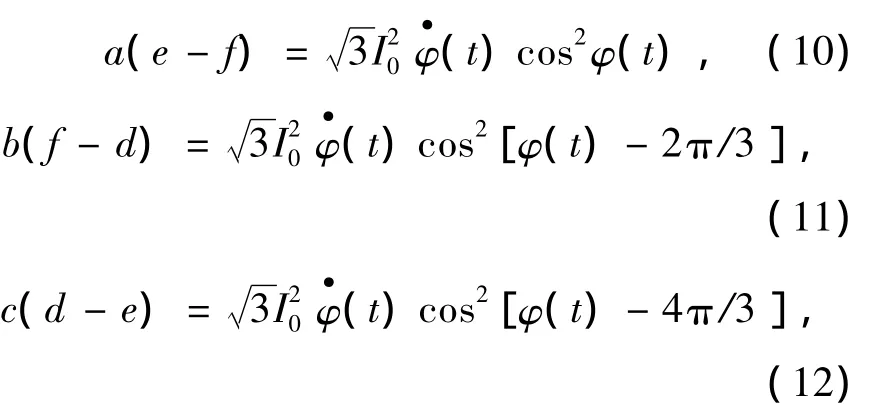
把 a(e－f)、b(f－d)、c(d－e)相加，得到:

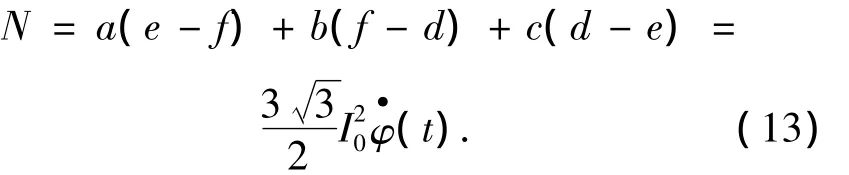
在实际环境中，光源强度波动及偏振态变化会使I0的值发生变化，为了消除对I0带来的影响，先把3个输入信号平方，可得:

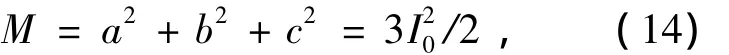
再用(13)式除以(14)消去I20，得:

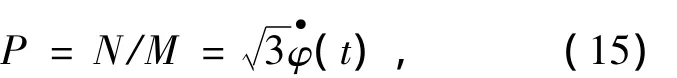
经积分运算后得到输出为:

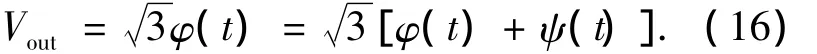
通常把ψ(t)当做慢变化量，经过高通滤波器即可滤除，从而解调出待测的信号φ(t)。

3 解调信号的频率范围

根据奈奎斯特采样定理，采样脉冲的频率fT由被采样信号的频带宽度来决定，频谱宽度为:

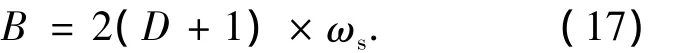
从式(17)看出，频谱宽度随着D的增加而变宽。为了方便起见，令D=1，根据工程经验，采样率一般为4～8倍的带宽。

干扰信号ψ(t)频率设为1 Hz，幅度是1的正弦信号;待解调信号φ(t)分别设为频率100 Hz与50 kHz，幅度10的正弦信号;采用8阶巴特沃斯高通滤波器进行Matlab仿真，结果分别如图3、图4、图5、图6所示。由结果可以看出3×3耦合器解调方法可以实现几十Hz到几十kHz的解调［13］。

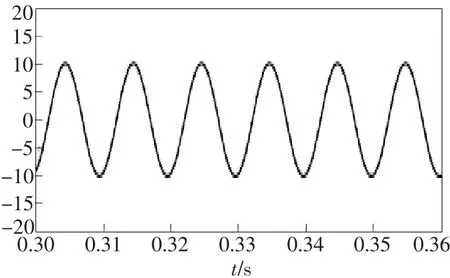
图3 频率为100 Hz的待解调信号的波形Fig.3 Signal waveform of 100 Hz frequency before demodulation

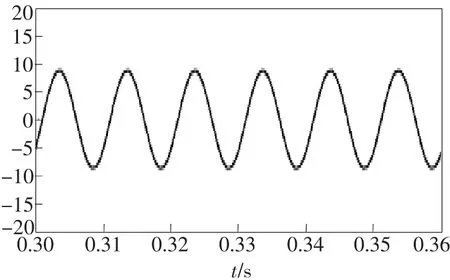
图4 频率为100 Hz的解调输出信号的波形Fig.4 Signal waveform of 100 Hz frequency through a highpass filter

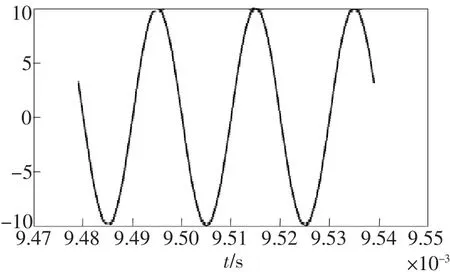
图5 频率为50 kHz的待解调信号的波形Fig.5 Signal waveform of 50 kHz frequency before demodulation

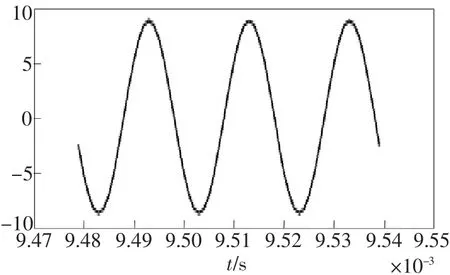
图6 频率为50 kHz的解调后输出信号的波形Fig.6 Signal waveform of 50 kHz frequency through a highpass filter

3.2 解调方法的干扰性分析

经过MATLAB仿真，待解调的干涉相位差信号如图7所示，未经滤波输出的解调信号如图8所示，滤波后输出的信号如图9所示。将3幅图的信号作对比可知，没有通过高通滤波器前，因为信号被干扰，信号的幅度有所失真;信号通过高通滤波后，幅度发生改变，但信号幅度的变化总趋势跟待解调信号基本保持一致。把图7、图8、图9某区间展开(起始和中止时刻一致)，分别得到图10、图11、图12。将这3幅图对比可知，通过高通滤波器后信号的相位与频率基本和原始信号一致。

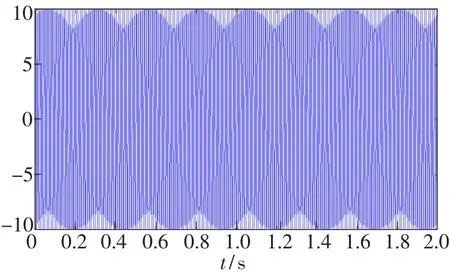
图7 待解调的干涉相位差信号Fig.7 Signal waveform before demodulation

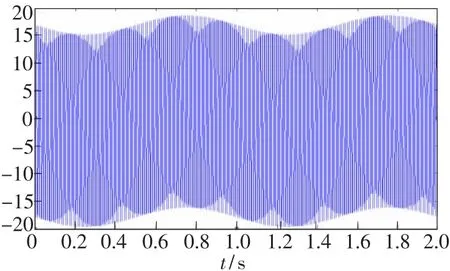
图8 未经滤波输出的解调信号Fig.8 Signal waveform through a high-pass filter before

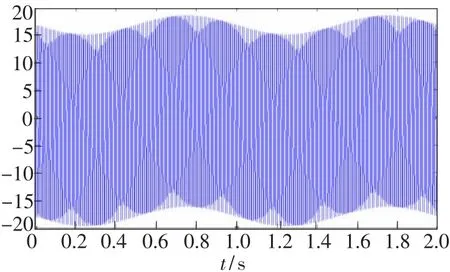
图9 经滤波输出的解调信号Fig.9 Signal waveform through a high-pass filter

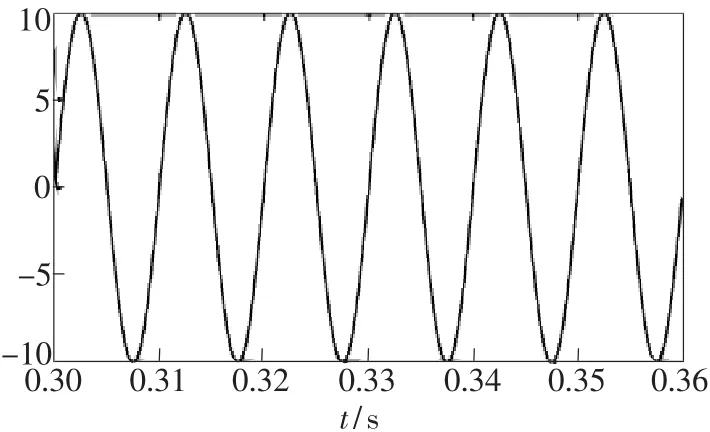
图10 待解调的干涉相位差信号Fig.10 Signal waveform before demodulation

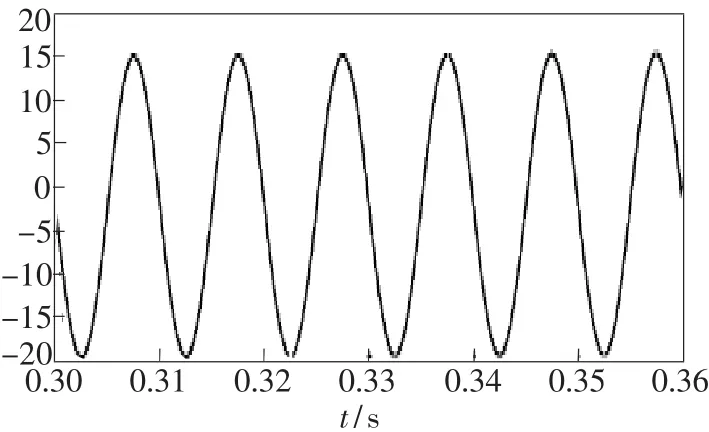
图11 未经滤波输出的解调信号Fig.11 Signal waveform through a high-pass filter before

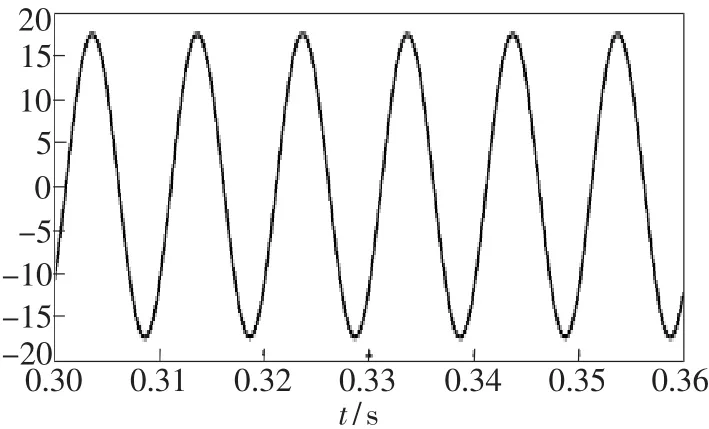
图12 经滤波输出的解调信号Fig.12 Signal waveform through a high-pass filter

通过对图(7)～(12)分析可知，只要让信号经过高通滤波器，并合理修改高通滤波器的参数，就可以滤掉外界温度变化带来的干扰，从而解调出干涉相位差 φ(t)［14］。

3.3 不对称性对信号解调结果的影响

上面的仿真中，3×3耦合器都是假定在理想分光比的情况下进行，即3个输出端互成120°。但实际应用中，3×3耦合器不可能是理想分光比，也就是说3×3耦合器的3个输出端不是互成120°，而是有一定的偏差［15-17］。下面用MATLAB仿真3×3耦合器3个输出端有10°偏差的解调情况。

对a=I0cos［φ(t)］的波形进行仿真，图13为3个输出端理想分光比情况，图14为3个输出端有10°偏差情况。将图13、图14比较可以看出，在干涉输出端有10°偏差对a的波形没有影响。

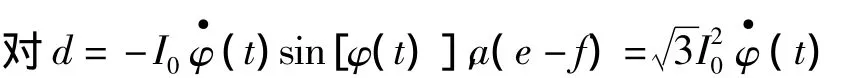
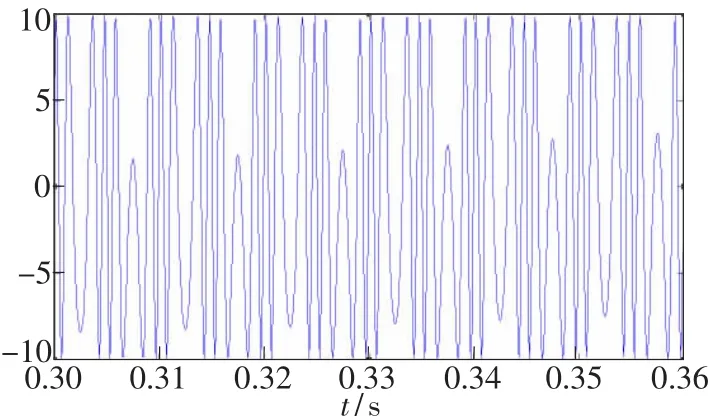
图13 3个输出端为理想分光比时的情况Fig.13 The three road output is ideal optical divide ratio

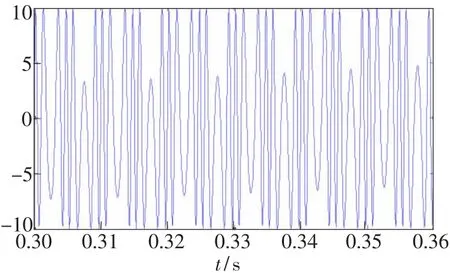
图14 3个输出端有10°偏差时的情况Fig.14 The three road output exists 10°deviation

对M=a2+b2+c2=3/的波形进行仿真，得到图21和图22，从中看出在理想情况下M的波形是直流，在3个输出端有10°偏差情况下，M的波形携带有谐波。

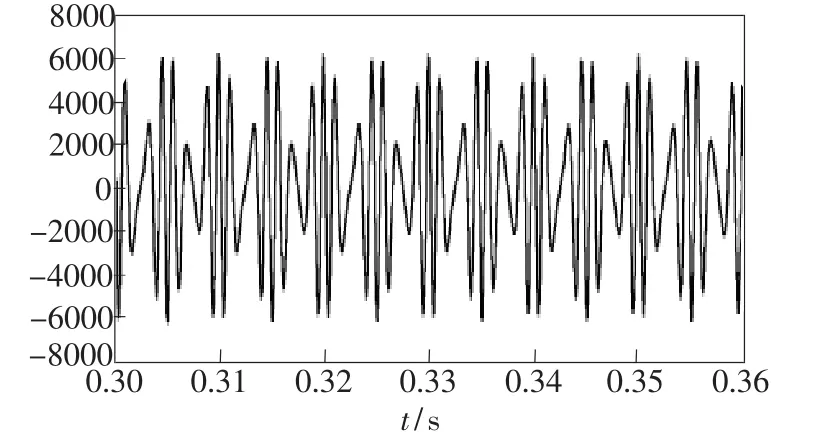
图15 3个输出端为理想分光比时的情况Fig.15 The three road output is ideal optical divide ratio

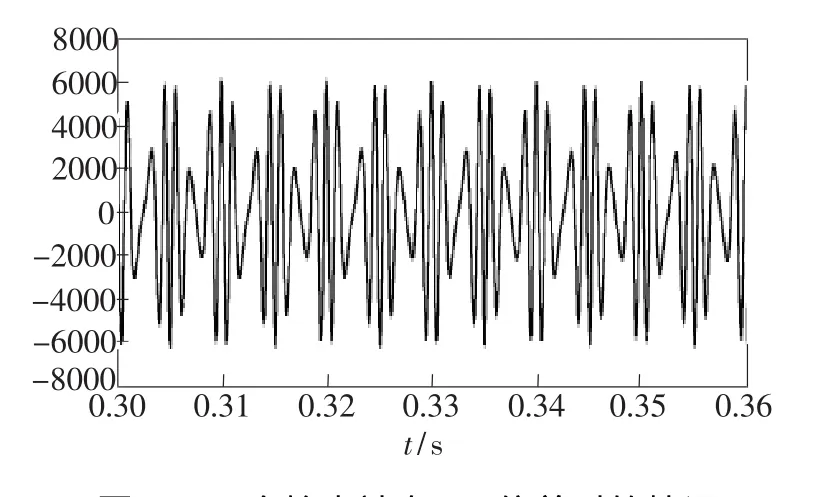
图16 3个输出端有10°偏差时的情况Fig.16 The three road output exists10°deviation

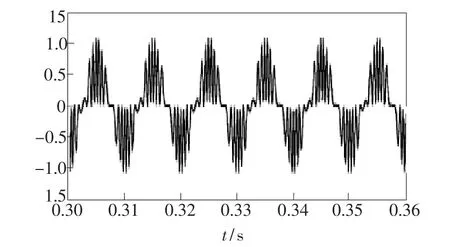
图17 3个输出端为理想分光比时的情况Fig.17 The three road output is ideal optical divide ratio

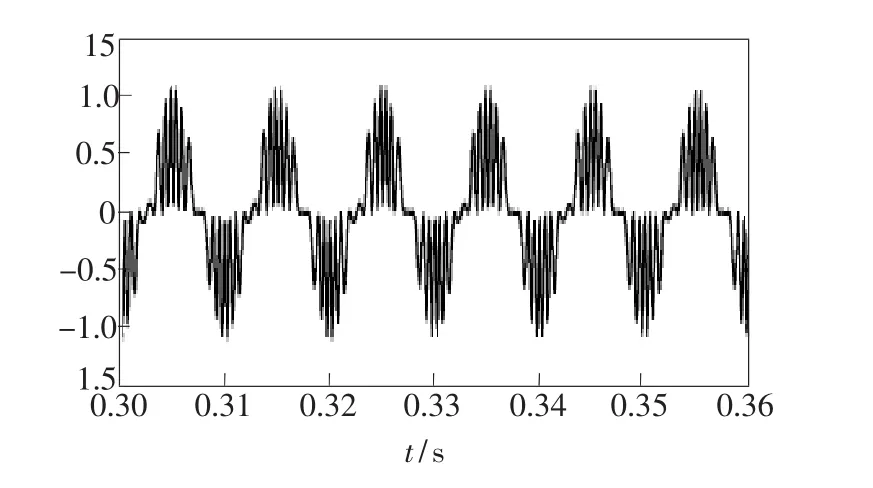
图18 3个输出端有10°偏差时的情况Fig.18 The three road output exists10°deviation

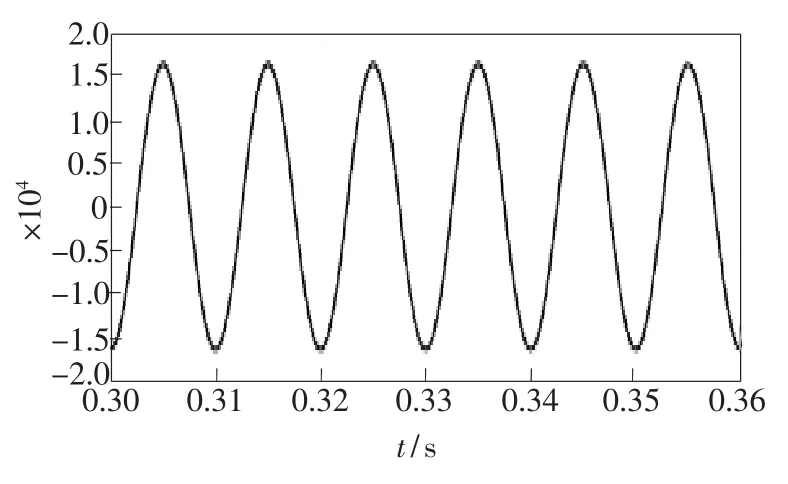
图19 3个输出端为理想分光比时的情况Fig.19 The three road output is ideal optical divide ratio

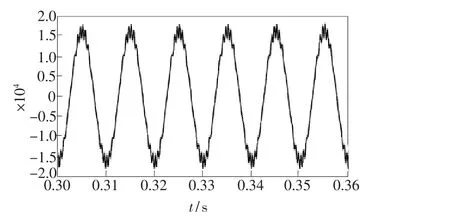
图20 3个输出端有10°偏差时的情况Fig.20 The three road output exists10°deviation

图21 3个输出端为理想分光比时的情况Fig.21 The three road output is ideal optical divide ratio

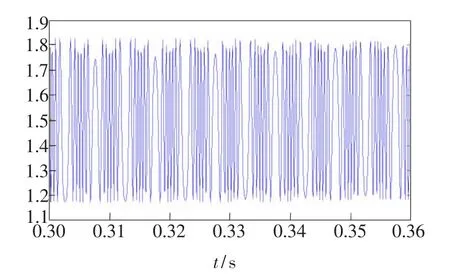
图22 3个输出端有10°偏差时的情况Fig.22 The three road output exists10°deviation

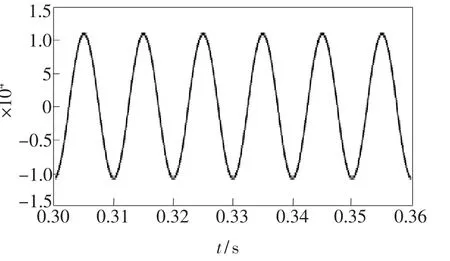
图23 3个输出端为理想分光比时的情况Fig.23 The three road output is ideal optical divide ratio

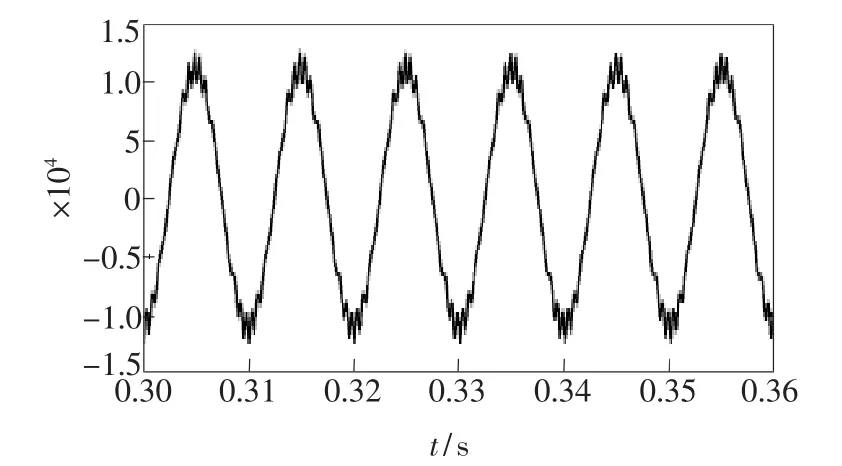
图24 3个输出端有10°偏差时的情况Fig.24 The three road output exists10°deviation

最后，对Vout=［φ(t)+ψ(t)］波形进行仿真得到图25，比较图24与图25，3个输出端有10°偏差的P=N/M =(t)的波形经过后续的积分处理，滤出了谐波。

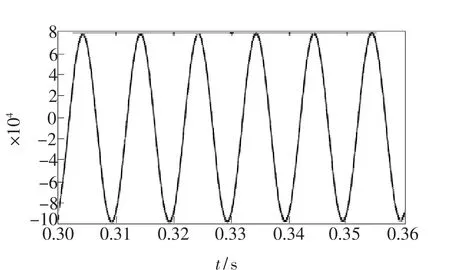
图25 经积分处理后的波形Fig.25 Waveform through integral

以上所做的MATLAB仿真是在3路输出的幅度相等的条件下进行的。耦合器不对称一定会引起信号的幅度不同。可以通过调节每一路信号的放大倍数来使3路输出信号的幅度相等。即使3×3耦合器3路输出的相位存在一定偏差，经过积分滤波后，解调结果也基本不会受到影响。

3.4 高次谐波对解调结果的影响

在上面仿真中，是假设待测信号是单一频率的正弦波，而在现实情况中，振动的信号里经常带有高次谐波成分。设一个输入的待解调信号为φ(t)=10sin(2πft)+5sin(6πft)+10sin(12πft)，并和上面一样设f=100 Hz，干涉仪的输入信号的波形为图26，解调后输出信号的波形为图27。比较图26和图27可看出，高频的部分虽然出现的轻微的噪声，但待测信号还是被准确的解调出来了。

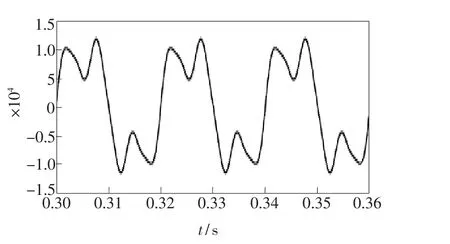
图26 含高次谐波的输入信号波形Fig.26 The input signal exists high order harmonic generation

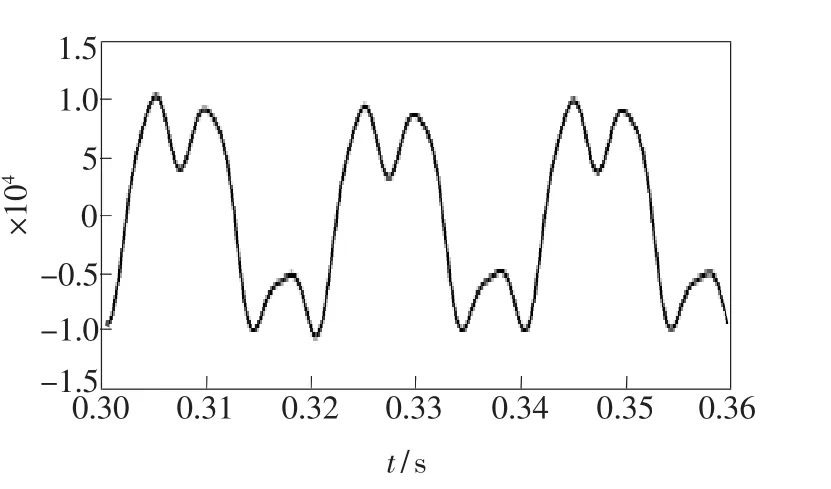
图27 解调后所得到的输出信号波形Fig.27 The output signal after demodulation

4 结 论

对3×3耦合器3路输出解调方法进行了仿真分析，证明这种解调方法有比较宽的解调频率范围，能够克服温度变化等导致的干扰，具有不需要载波、不需要稳定的工作点、抗干扰能力强等诸多优点。耦合器解调方法稳定、可靠、简便、不需要调制光源，具有较强的实用性和可行性。本文的研究结果对解调电路的数字化设计具有理论指导意义。

［1］Koo K P，Tveten A B.Passive stabilization scheme for fiber interferometers using(3×3)fiber directional couplers［J］.Appl.Phys.Lett.，1982，41(7):616-618.

［2］Sheem S K，Giallorenzi T G，Koo K P.Optical techniques to solve the signal problem in fiber interferometers［J］.Appl.Opt.，1982，21(4):689-693.

［3］Hong G W，Jia B，Hua Z Y.A novel passive demodulator for fiber optic interferometer with 3×3 coupler［J］.Chin.J.Sci.Instrum(仪器仪表学报)，2006，27(4):341-344(in Chinese).

［4］Huang T H，Cao W H.Fiber coupler and its applications［J］.Electro-Opt.Technol.Appl.(光电技术应用)，2006，21(6):37-41(in Chinese).

［5］Brown D A，Cameron B，Keolian R M，et al.A symmetric 3×3 coupler based demodulator for fiber optic interferometric sensors［J］.SPIE，1991，1584:328-335.

［6］Jiang Y，Chen S F.Direct demodulation for signal from fiber grating sensors by interferometer based on 3×3 coupler［J］.Acta Optica Sinica(光学学报)，2004，24(11):1487-1490(in Chinese).

［7］Zhang Y B，Dou Z，Cao J N.3-output demodulation of interferometric fiber-optic hydrophone［J］.J.Harbin Eng.Univ.(哈尔滨工程大学学报)，2004，25(6):732-735(in Chinese).

［8］Zhao Y C，Wang H，Jian S S.Mach-Zehnder optical fiber interferometer homodyne scheme［J］.Opt.Commun.Technol.(光通信技术)，2001，18(3):187-191(in Chinese).

［9］Dandridge A，Wang C C，Tveten A B，et al.Performance of 3×3 couplers in fiber optic sensor systems［J］.SPIE，1994，2360:549-552.

［10］Chen D S，Xiao L，Cui J，et al.Analysis of 3×3 coupler demodulation method for optical fiber interferometer and polarization fading［J］.J.Optoelctronics·Laser(光电子·激光)，2007，18(5):523-525(in Chinese).

［11］Jiang Y.Wavelength division multiplexing addressed four-element fiber optical laser hydrophone array ［J］.Appl.Opt.，2007，46(15):2939-2948.

［12］Wang J H，Meng J，Chen C H，et al.Design scheme of intelligent instrument interface and digital processing system［J］.Chin.J.Sensors and Actuators(传感技术学报)，2005，18(1):284-288(in Chinese).

［13］Jiang Y，Lou Y M，Wang H W.Software demodulation for 3×3 coupler based fiber optic interferometer［J］.Acta Photonica Sinica(光子学报)，1998，27(2):152-155(in Chinese).

［14］Gao X M.Evolution of fiber optic hydrophones and hydrophone arrays［J］.Optical Fiber＆ Electric Cable and Their Applications(光纤与电缆及其应用技术)，1996，29(1):48-53(in Chinese).

［15］Sheem S K.Optical fiber interferometers with 3 × 3 directional couplers analysis［J］.J.Appl.Phys.，1982，52(6):1267-1277.

［16］Todd M D，Seaver M，Bucholtz F.Improved，operationally-passive interferometric demodulation method using 3×3 coupler［J］.Electron.Lett.，2002，38(15):784-786.

［17］Shen L，Ye X F，Li Z N.Research on demodulation of interferometric fiber optic hydrophone［J］.Semiconductor Optoelectronics(半导体光电)，2001，22(2):105-106(in Chinese).