光学分数阶混沌系统的控制研究

张 培， 乔宗敏

（1.合肥师范学院数学系，安徽 合肥230601；2.安徽大学数学科学学院，安徽合肥230601）

1 引言

分数阶微积分理论的研究到目前为止已经有300多年的历史，且分数阶混沌系统及其应用成为现在自然科学研究的一个热点问题［1－10］，分数阶混沌的研究已经步入一个新的领域，呈现出新的发展趋势，两个不同参数混沌系统的同步研究；由连续的混沌系统转向离散的混沌系统的研究；由低维的混沌系统转向高维的超混沌系统的研究；新的同步方法不断提出等等.故而无论从分数阶混沌系统的控制与同步的方法上，还是现有的文献数量上，都尚处于研究初期。

本文研究一类分数阶光学混沌系统的控制和同步方法，利用非线性反馈控制方法设计混沌同步控制器实现了在平衡点处的稳定控制，并通过对所得的混沌同步控制器进行了仿真模拟，验证了方案是有效的。

2 分数阶光学混沌系统

对分数阶导数的概念有多种定义，这里采用如下 Caputo微分定义［11－12］如下：

分数阶光学混沌系统［13］为：

通过计算可以得到了系统的三个平衡点：E1（0，0，0），E2（1，0，0），E3（－1，0，0）。

系统的雅克比矩阵为

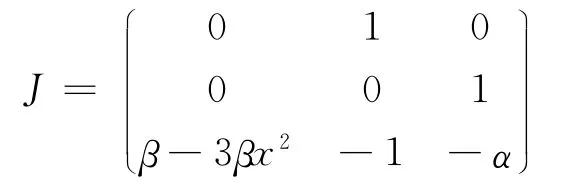
其中，α，β为正实数，且q＝（q1，q2，q3）是分数阶，当q＝（1，1，1）时，系统（1）取参数α＝0.35，β＝0.6时，系统将会出现混沌性态，有一个混沌吸引子，如图1所示。

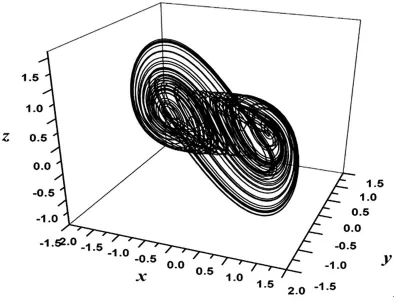
图1 分数阶混沌吸引子α＝0.35，β＝0.6

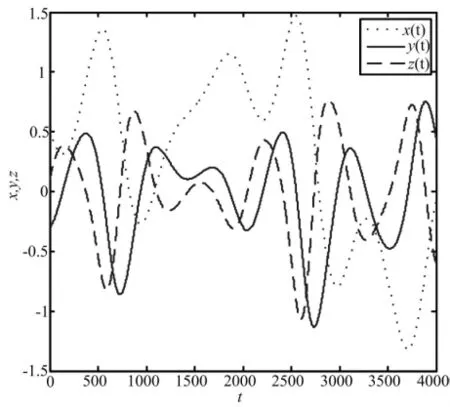
图2 分数阶混沌的三个状态变量α＝0.35，β＝0.6

3 分数阶光学系统的控制器设计

引理1［11］分数阶线性微分方程为：Dqx（t）＝Ax（t），x（0）＝x0，其中：x∈Rn，矩阵A∈Rn×Rn，q＝［q1，q2，…，qn］，0＜qi＜1，i＝1，2，…，n是分数阶导数，则系统渐近稳定的充要条件是｜arg（λi）｜＞，其中：λi是A的特征值.

引理2［12］设0＜qi＜1，i＝1，2，…，n，都是有理数记 M 是m，ii＝1，2，…，n，为最小公倍数，则非对称分数阶线性系统渐近稳定的充要条件是其中：λ是｜diag（λmq1，λmq2，…，λmqn）－A｜＝0的根.

对于对称的光学分数阶混沌系统（1）：DqX＝AX＋Φ（X），

设计反馈控制器U＝－Φ（X）＋BX，则控制系统为：

选择合适控制矩阵B使得线性控制系统稳定，便可以实现该新的分数阶混沌系统（1）在平衡点的稳定控制。

定理1 对于分数阶混沌系统（1），为了将系统稳定控制在E1（0，0，0），设计如下控制器：U＝－Φ（X）＋BX，

则分数阶控制系统DqX＝AX＋Φ（X）＋U 的轨道被稳定控制在E1（0，0，0）.

证明

其中：λi是矩阵A＋B的特征值，由引理1知，DqX＝（A＋B）X系统渐近稳定，从而该新的分数阶混沌系统（1）被稳定控制在平衡点E1（0，0，0）.

定理2 对于分数阶混沌系统（1）平移后的系统（2）DqX＝AX＋Φ（X），将系统（2）稳定控制在不稳定的平衡点E2，设计如下控制器：

则分数阶混沌系统（1）的轨道被稳定控制在E2（1，0，0）.

证明 为实现在不稳定点E2（或E3）处的稳定控制，把平衡点由E2平移到（0，0，0），所以做变换：

则该系统变形为：

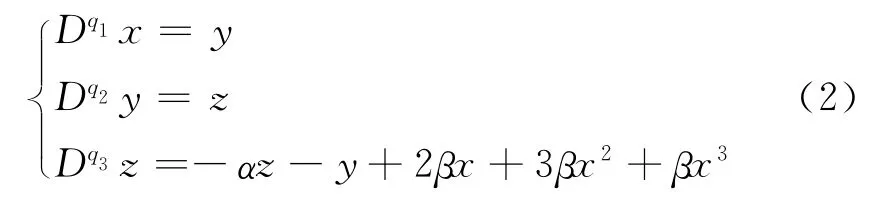
引入控制U＝－Φ（X）＋BX，则：DqX＝（A＋B）X，经计算得：

其中：λi是矩阵A＋B的特征值，由引理1知，DqX＝（A＋B）X系统的渐近稳定，从而该新分数阶混沌系统（1）被稳定控制在平衡点E2（1，0，0）.

注2 考虑分数阶导数不相等且0＜qi＜1，i＝1，2，…，n，都是有理数的情形，利用引理2的结论，适当选择矩阵B，使得λ是｜diag（λmq1，λmq2，…，λmqn）－A｜＝0的根，也可以实现非对称该分数阶混沌系统的稳定控制。

注3 对于不稳定点E3的稳定控制方法类似，这里省略。

4 分数阶系统的数值仿真

分数阶微分方程不能用ODE方法求解，常见的分数阶系统的数值解法有拉普拉斯变换法、傅立叶变换法和预估－校正算法等，这里采用预估－校正算法设计程序求解该新分数阶混沌系统初值问题及其控制系统。

其中

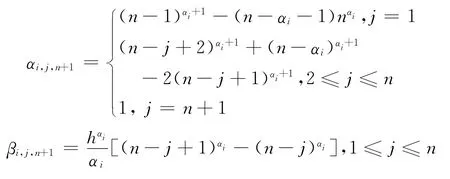
实验中，系统参数为α＝0.35，β＝0.6，（α1，α2，α3）＝（0.96，0.97，0.98），如图3为系统在平衡点E1（0，0，0）处三个状态的控制曲线，取初始值（x（0），y（0），z（0））＝（8，5，－7）。图4所示的是系统在平衡点E2（1，0，0）处三个状态的控制曲线，取初始值（x（0），y（0），z（0））＝（8，5，－7）。

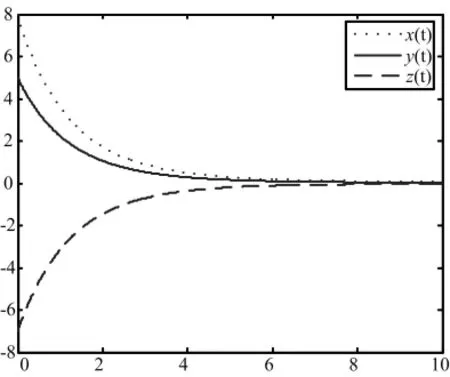
图3 分数阶（1）系统的平衡点E1（0，0，0）处的稳定控制

图4 分数阶（1）系统的平衡点E2（1，0，0）处的稳定控制

［1］Chen G，Yu X.On time－delayed feedback control of chaotic systems［J］.IEEE Trans Circ Syst I 1999，46：767－72.

［2］Xu N，etc.A hybrid chaos optimization menthod and its application［J］.Sys Engin and Electr，2003，25（2）：226－228.

［3］Ott E，Grebogi C，Yorke J A.Controlling chaos［J］.Phys Rev Lett 1990，64：1196－1209.

［4］Shangbo Zhou，Hua Li，Zhengzhou Zhu.Chaos control and synchronization in a fractional neuron network system［J］.Chaos，Solitons ＆ Fractals 2008，36：973－84.

［5］I.Grigorenko，E.Grigorenko，Chaotic dynamics of the fractional Lorenz system［J］.Phys.Rev.Lett.2003，41－61.

［6］Li C，Chen G.Chaos in the fractional order Chen system and its control［J］.Chaos，Solitons ＆ Fractals 2004，22：549－54.

［7］Tavazoei MS.Chaotic attractors in incommensurate fractional order system［J］.Physics D，2008，237：2628－2637.

［8］C.Liu，L.Liu，T.Liu，A novel three－dimensional autonomous chaos system［J］.Chaos Solitons Fractals 2009，39：1950－1958.

［9］H.H.Chen，Global synchronization of chaotic systems via linear balanced feedback control［J］.Appl.Math.Computat.2007，186：923－931.

［10］T.Botmart，P.Niamsup，Adaptive control and synchronization of the perturbed Chua’s system［J］.Math.Comput.Simul，2007，75：37－55.

［11］I.Podlubny，Fractional Differential Equations［M］.San Diego：Academic Press，1999，62－70.

［12］S.G.Samko，A.A.Kilbas，O.I.Marichev，Fractional Integrals and Derivatives［M］.Gordon and Breach，Yverdon：Theory and Applications，1993，60－78.