小型磁偏转质谱计离子源性能参数的模拟研究

张文台，郭美如，肖玉华，赵以德，李得天

(兰州空间技术物理研究所，真空低温技术与物理重点实验室，甘肃兰州730000)

1 引言

磁偏转质谱计稳定性和定量性好、丰度灵敏度高，被广泛应用在星球探测、航天器环境分析、食品安全、药物检测、工业过程控制等诸多领域［1］。电子轰击型离子源(Electron Impact Ion Source，简称EI源)由于其设计结构简单、可靠性高，被广泛应用于空间小型磁偏转质谱计［2］，目前商业用质谱－色谱联用仪的离子源多数为EI源［3］。聚焦和离子引出效率是离子源重要的性能指标，其中离子源的聚焦性能直接影响质谱计的分辨率，引出效率直接影响质谱计的分析灵敏度［4］。对于传统的EI源由于其离子产额较小，离子束流强度弱，使得灵敏度偏低。然而理想的离子源要求离子束流强度大、散角小、能量分散小且束流稳定等［5，6］。因此提高EI源的聚焦性能和离子引出效率具有十分重要的意义。从EI源内离子的初始分布和EI源电参数出发，利用离子光学仿真软件SIMION－3D8.0，建立了质谱计EI源的物理模型，采用相空间的分析方法，通过数值计算的方法研究了EI源内离子初始分布和电参数对其聚焦性能和离子引出效率的影响。

2 离子源结构

离子源结构如图1所示。由电离室B、电离室出口狭缝、聚焦磁铁、灯丝、推斥极R、聚焦极H、主狭缝S和α狭缝组成。电离室加扫描电压，范围为200～2 100 V，其它各电极电压都以扫描电压为参考电压。由推斥电极R、电离室B和聚焦电极H1、H2构成的静电透镜，使离子聚焦在主狭缝S附近，能够获得最强离子流。α缝限制离子束在水平方向的散角。

图1 离子源结构

3 离子轨迹计算及相空间分析方法

3.1 离子轨迹计算

SIMION－3D8.0软件包主要用来计算带电粒子在特定电极(不同电势、材料、带电状态、几何形状等)产生的电场中的运动轨迹［7］，程序提供了强大的计算功能，并且可使结果可视化，用户通过建立几何模型、编写用户程序来完成复杂的计算。在SIMION－3D8.0中首先编写几何文件1.gem，定义一个离子源的三维静电势点阵列［8］，每个电极都是独立的电势点阵列，如图2(a)是三维示意图，图2(b)是剖视图，图中字母代表各个电极。这些电势阵列是由三维的点阵列组成的长方体阵列构成。

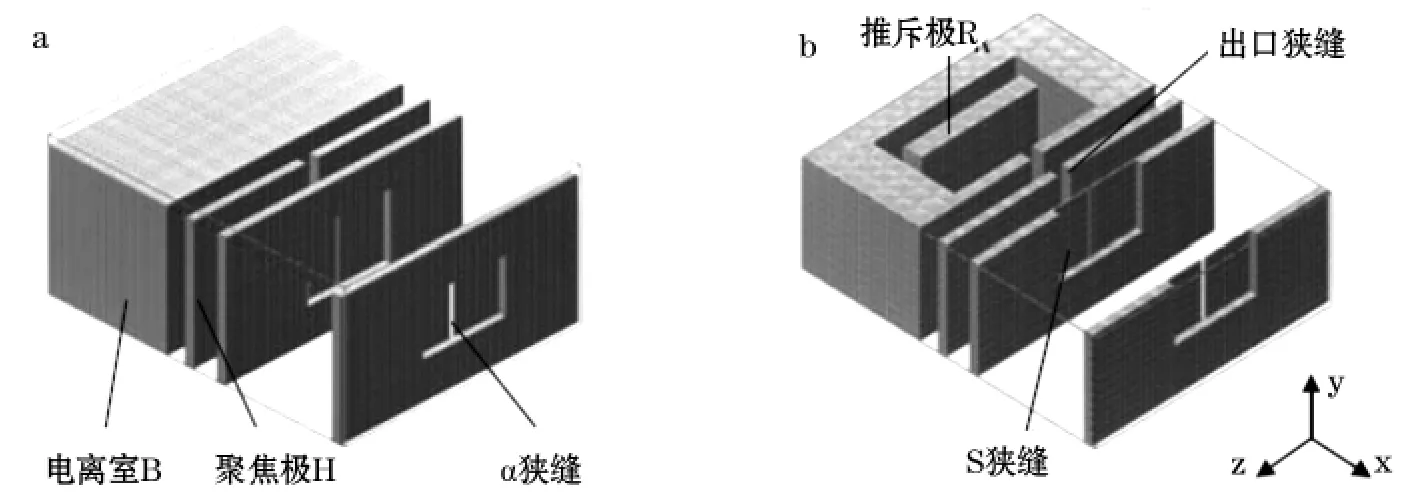
图2 SIMION8.0中的离子源模型

当电势阵列中的点限制在特定的电极和非电极范围内时，SIMION－3D8.0就可以通过求解Laplace方程(1)，利用有限元方法计算三维阵列空间中任意点的电势［9］:

再利用四阶－龙哥库塔法计算离子在电场中的运动轨迹［8］

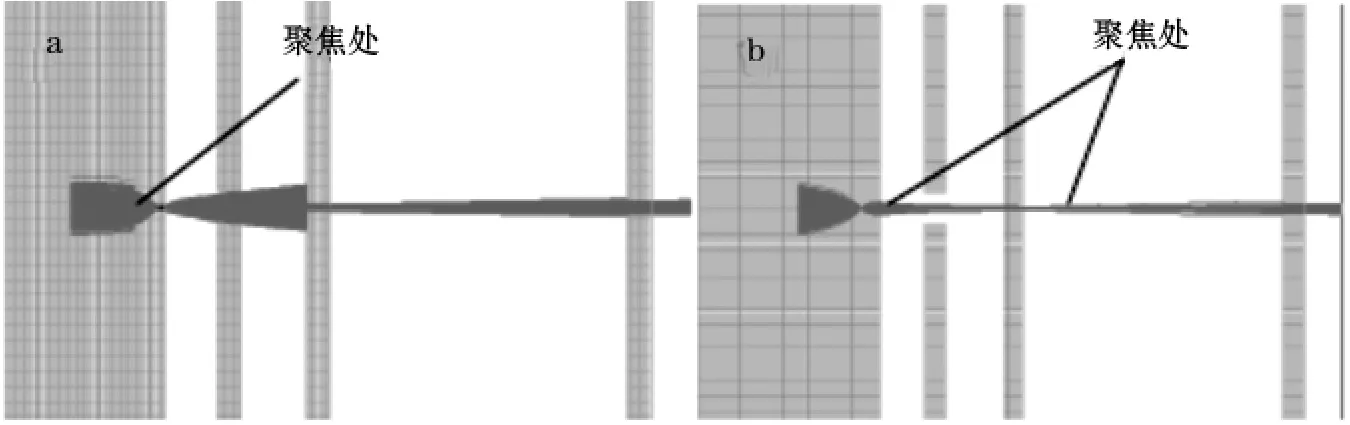
图3 离子在离子源内的运动轨迹

从图3(a)中可以看出，离子在引出的过程中，一部分被电离室引出狭缝阻拦，引出后的离子束聚焦后通过主狭缝S和α狭缝传输到质量分析器。为了提高离子源分辨率，主狭缝设计的非常小，从而主狭缝S也会阻挡一部分离子，离子传输到α狭缝处时也会被阻挡一部分，因而引出离子的有效利用率是非常小的，本文对如何提高离子的有效利用率进行了研究，从离子的聚焦和引出效率出发来探讨离子源的性能。对于引出效率的研究通过编写用户程序(User Program)记录引出的离子数来计算引入到分析器的离子占离子源内离子数的比例。对于聚焦性能的研究采用相空间分析方法［10，11］。

3.2 相空间分析方法

在一个由许多粒子构成的体系中，某一粒子于某一瞬时的运动状态可用它的位置p和速度v来描述，它在直角坐标系中的分量分别是x，y，z;vx，vy，vz，该六个物理量定义的六维空间，称为相空间。若离子的p点和v点值已确定，那么它在相空间的位置也随之确定，且随着粒子的运动状态变化而变化。扫描电压VB加在电离室上，推斥极电压VR，聚焦电压VH。离子源的中心线坐标为(x，7.0，10.0)，所有狭缝的中心都在离子源中心线上，离子出口狭缝的宽度设定在z方向，因此离子束的聚焦发生在z方向上，初始离子按高斯分布随机产生500个离子［12］。图4为离子在z方向上聚焦的相空间图形，设定离子初始能量为0，那么它在相空间图形中是一条平行于z轴数值为0的直线，从图4分析可知离子引出电离室聚焦后，位置聚焦半径为0.06 mm(狭缝宽为0.2 mm)，速度聚焦半径为4 mm，说明离子源有很好的位置聚焦性能，但是速度聚焦性能较差，位置聚焦和速度聚焦无法同时实现。

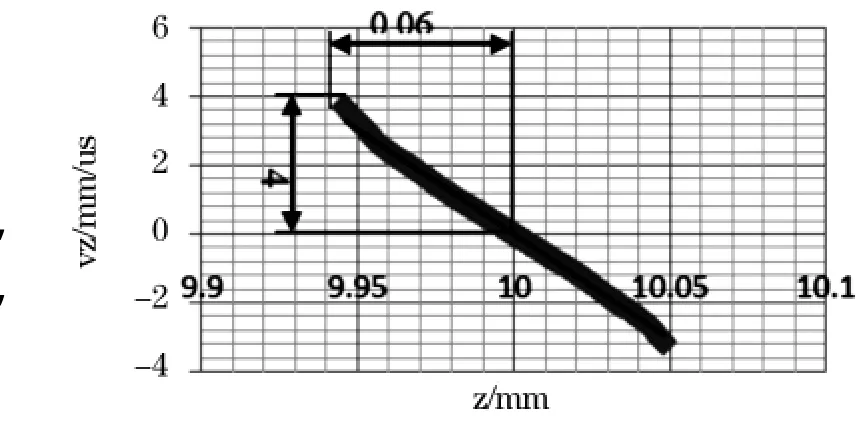
图4 离子在z方向上聚焦处的相空间图形

4 结果分析与讨论

4.1 离子初始分布对聚焦和引出效率的影响

在SIMION－3D8.0内设定离子在x，y，z方向的初始位置分别为6.2、7.0、10，初始动能为 0 eV，随机产生 500 个离子，扫描电压 VB=250 V，VR－VB=6 V，VH=50%VB。图5(a，b，c)分别为初始离子沿x，y方向无分散，沿z方向分别分散在0.05，0.1，1.5，2.0，2.5，3.0，3.5，4.0，4.5，5.0 的范围内时，由相空间分析得到的位置聚焦半径、速度聚焦半径以及离子的引出效率与z方向初始分布的关系，图6(a，b，c)分别为初始离子沿 y 方向无分散，沿 z方向分散为0.3，沿 x 方向分别随机分散在0.05，0.1，0.15，0.2，0.25，0.3 的范围内时，由相空间分析得到的位置聚焦半径、速度聚焦半径以及离子的引出效率与x方向初始分布的关系。

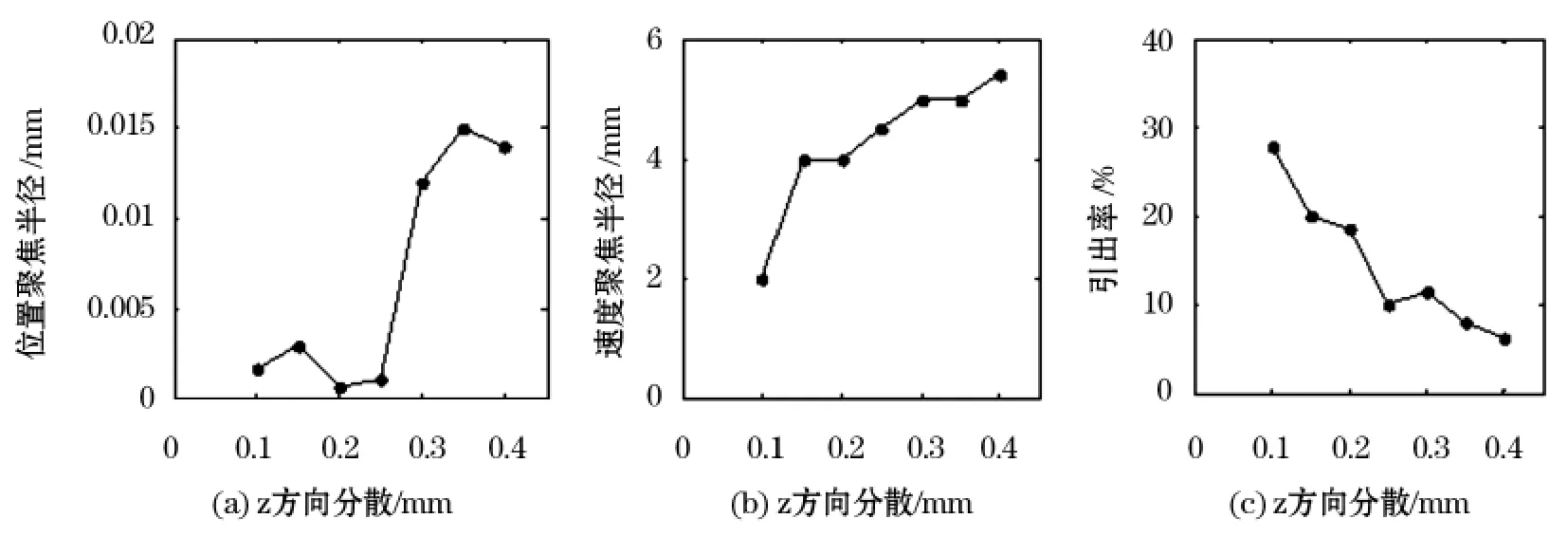
图5 z方向离子分散范围与聚焦半径和离子引出效率的关系

图6 x方向离子分散范围与聚焦半径和离子引出效率的关系

从图5分析可得，随着狭缝方向(z方向)初始分散的增大，位置聚焦半径和速度聚焦半径都增大，离子引出效率减小，说明随着z方向离子初始分散的增大，离子源聚焦性能和引出效率都变差。从图6分析可得，当初始离子x方向有分散时，位置聚焦半径(图6a)比在x方向无分散时(图5a)增大了一个数量级，速度聚焦半径不变，引出效率明显下降，这是由于当气体分子的电离发生在整个电离室内时，由于远离出口缝的离子在电离室内运动，经电场加速的距离不同，使得它们在出口处的动能不同，从而影响离子的聚焦和引出效率，同时也容易引起较大的像差［9］。

从上面的分析可知，使电离室内气体分子的电离尽可能多的发生在电离室出口狭缝附近，这样才能保证更好的离子聚焦性能和高的离子引出效率。而且远离狭缝的离子即使被引出，这部分离子由于引出距离和时间长而引起像差，影响质谱计的分辨率。

4.2 离子源电参数对离子聚焦和引出效率的影响

4.2.1 聚焦极电压对离子聚焦和引出效率的影响

离子在 x，y，z方向的初始位置分别为 6.2、7.0、10，在 x，y 方向上无分散，在 z方向上的分散为 0.3，初始动能为0eV，随机产生500个离子，扫描电压VB=250 V，VR－VB=6V，分别按聚焦极电压VH所占扫描电压VB的百分比给聚焦极VH分配电压，研究聚焦电极对离子聚焦和引出的影响，如图7(a，b，c)所示。

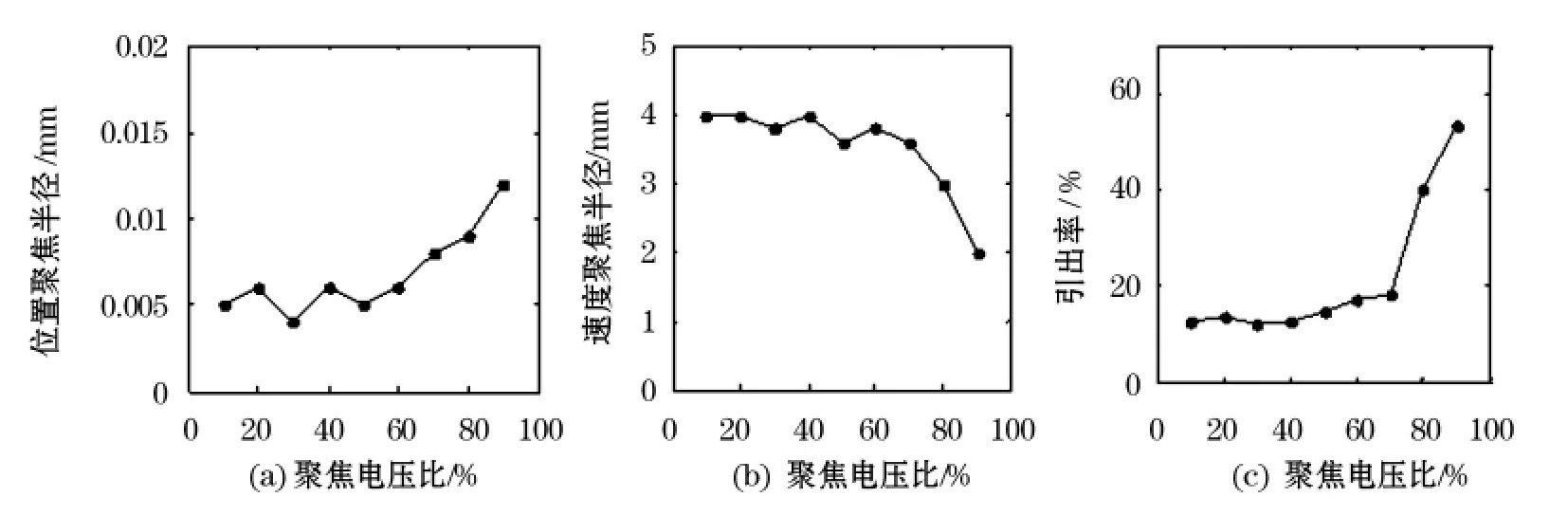
图7 聚焦电压比与聚焦半径和离子引出效率的关系

从图7可以看出，随着聚焦极电压比的增大，位置聚焦半径增大，速度聚焦半径减小，离子引出效率增大。

4.2.2 推斥极电压与扫描电压差对离子聚焦和引出效率的影响

离子在 x，y，z方向的初始位置分别为 6.2、7.0、10，在 x，y 方向上无分散，在 z方向上的分散为 0.3，初始动能为0 eV，随机产生500个离子，VH=50%VB，图8(a，b)分别为扫描电压VB=250 V时推斥极电压与扫描电压差VR－VB跟位置聚焦半径、速度聚焦半径的关系，由图8分析得VR－VB对位置聚焦和速度聚焦的影响不大，因此我们只研究VR－VB与离子引出效率的关系。其它初始条件不变，设定扫描电压VB分别取250 V，500 V，1200 V，2100 V，研究推斥极电压与扫描电压差VR－VB对离子聚焦和引出的影响，如图9所示。

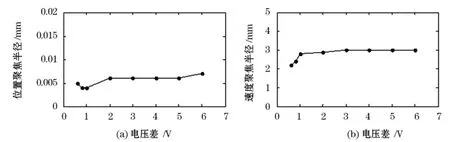
图8 推斥极电压和扫描电压差与聚集半径的关系

从图9中分析可得，扫描电压小于250 V时，VR－VB的差值取1V就能得到很好的引出效率，随着扫描电压的增大，若增大电压差VR－VB，离子的引出效率也随之增大。但当电压差的值过小时，由于扫描电压本身的波动误差，在工程中是很难实现的，所以综合各种因素，取电压差VR－VB的值为3V时，结果最理想。

4.2.3 主狭缝S和α狭缝加电时对聚焦和离子引出效率的影响

在前面的分析中，主狭缝S和α狭缝都不加电，在仿真研究中发现，当S极和α狭缝分别加负偏压时，离子在传输过程中能够实现两次聚焦(如图3(b))，当第一次聚焦在出口狭缝与聚焦极之间，第二次聚焦在主狭缝极S附近时，具有很好的聚焦性能和引出效率。离子在 x，y，z方向的初始位置分别为 6.2、7.0、10，在 x，y方向上无分散，在z方向上的分散为0.3，初始动能为0 eV，随机产生500个离子，扫描电压 VB=250 V，VR－VB=1V，VH=50%VB。图10(a，b)分别为主狭缝电压分别为S=－100 V和S=－400 V时α狭缝电压与位置聚焦半径、速度聚焦半径的关系。

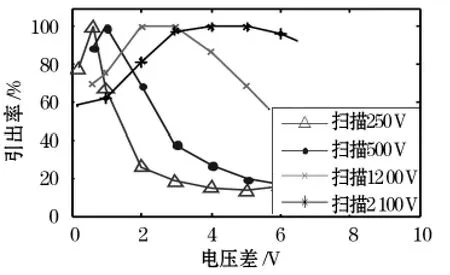
图9 推斥极电压和扫描电压差与离子引出效率的关系

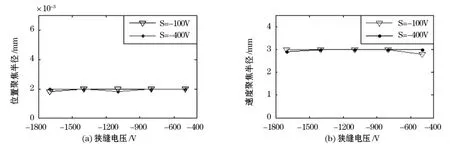
图10 主狭缝S加电时，α狭缝电压与聚焦半径的关系

从图10中可以看出看出，当改变S极和α极电压时，离子聚焦性能基本保持不变，且聚焦性能都很好。下列讨论S，α极电压与引出效率的关系。

图11 α狭缝和主狭缝S电压与离子引出效率的关系

从图11(a，b)分析可得，S=－400 V时，任意改变α电压，离子引出效率都大于90%，但从空间质谱计能耗的角度考虑，α偏压过高不易实施，分析图11(b)可以得到，在扫描电压较低时，取S=－400 V，α=－500 V时，离子源具有很好的引出效率。

从以上的分析可知，随着扫描电压的增大，相应增大推斥电压与扫描电压差，会得到很好的离子引出效率，但当推斥电压与扫描电压差很小时，实验中难以实现，发现当S和α狭缝加上负偏压时能够在推斥电压与扫描电压差较小的情况下提高离子束的引出效率，并且实现在离子束传输过程中两次聚焦。

5 结论

利用离子光学软件SIMION－3D8.0计算了质谱计EI源的离子运动轨迹，利用相空间分析方法分析了离子聚焦。结果表明，当EI源内气体分子的电离尽可能多的发生在离子室出口狭缝附近时，能更好的保证高的聚焦性能和好的引出效率。通过对EI源电参数的研究表明，当聚焦电压比增大时，离子的引出效率和位置聚焦半径相应增大;随着扫描电压的增大，相应增大推斥电压与扫描电压差，会得到很好的引出效率，当S、α狭缝加负偏压时能够使离子束在传输过程中两次聚焦，从而得到很好的聚焦性能和引出效率。本模拟结果能够对离子源的设计和优化提供重要的理论依据和实验指导。

［1］郭美如，李得天，肖玉华，等.小型磁偏转质谱计磁场的分析计算［J］.真空与低温，2010，16(1):12－13.

［2］Pomona，Calif.Two gas atmosphere sensor system(Mass Spectrometer)［R］.Washington，D，C.APEIL:National aeronautics and space administration，1970.

［3］S.DAGAN，A.AMIRAV.Electron Impact Mass Spectrometry of Alkanes in Supersonic Molecular Beams［J］.Am Soc Mass Spectrorn，1995，6:120－131.

［4］韦冠一，翟利华，张子斌，等.MAT261型离子源及离子透镜系统的仿真与实际应用［J］.质谱学报，2005，26(增刊):99－100.

［5］J.R.AHN，C.J.PARK.Computer simulation of electron and ion trajextories in electron－impace ion sources of a quadrupole mass spectrometer［J］.Nuclear Instruments and Methods in Physics Research A.2011，645:345－394.

［6］季欧.质谱分析［M］.第一版.北京:原子能出版社，1978:17.

［7］M.M.Abdelrahman，F.W.Abdelsalam.Computer investigation of ion beam optics for a Freeman type ion source system［J］.Nuclear Instruments and Methods in Physics Research B，2011，269:1761－1766.

［8］DAVID J MANURA.SMION 3D Version8.0.4 User‘s Manual［A］.Idaho:Idaho National Engineering and Environmental Laboratory，2008.

［9］I.Y XIMEN，ZL XU，ZX LIU.Design and calculation of an electron impact storage ion source for time－of－flight mass spectroneters［J］.International Journal of Mass Spectrometry and Ion Processes，1997，161:91－96.

［10］黄超，赵学.基于相空间方法的电子轰击离子源参数对其性能影响的研究［J］.真空科学与技术学报，2011，31(2):169－173.

［11］华中一，顾昌鑫.电子光学［M］.第二版.上海:复旦大学出版社，1993:390.

［12］IAN G.BROWN.ThePhysics and Technology of Ion Sources［M］.Second Revise.WILEY－VCH Verlag Gmb H ＆ Co.KGaA，Weinheim，2004:38.