具年龄和加权的半线性种群系统的最优边界控制
付 军, 朱 宏
(1. 吉林师范大学 数学学院, 吉林 四平 136000; 2. 吉林师范大学 计算机学院, 吉林 四平 136000)
0 引言及预备知识
目前, 关于生物种群系统最优控制问题的研究已取得许多成果. 例如: 文献[1]讨论了一类时变种群系统的最优边界控制问题; 文献[2]应用惩罚移位法研究了其最优边界控制的计算; 文献[3]讨论了具最终状态观测的时变种群系统的最优边界控制问题; 文献[4]针对生育率和死亡率均依赖于个体年龄的情形, 提出了具有加权规模的数学模型, 并讨论了其最优收获问题; 文献[5]研究了具有年龄分布和加权的非线性种群系统的最优分布控制问题. 本文进一步讨论如下具年龄和加权的半线性种群系统(P):
的最优边界控制问题, 其中:p(r,t)表示时刻t、 年龄为r的单种群密度;p0(r)表示t=0时种群的年龄密度初始分布; 常数T表示生物种群的控制周期;f表示时刻t、 年龄为r的种群系统的外界扰动函数;S(t)表示时刻t种群的加权总量;ω为权函数;u为控制变量;β和μ分别为生物种群的出生率和死亡率, 这里μ和β均与权函数ω有关, 体现了加权总规模对种群动态过程的影响, 因而, 更具有实际意义;A表示种群个体能活到的最高年龄,r∈(0,A), 0 p(r,t)=0,r≥A. (5) 由于状态方程(1)-(4)的解依赖于u, 所以记为p(r,t;u)或简记为p(u), 人们希望通过控制函数u(t), 使系统(P)的状态更接近种群密度的理想状态zd(r,t). 为此, 引入如下性能指标泛函: (6) 假设如下条件成立: (H1)g,h:R→R+为凸函数,g,h∈C(R+)且g′,h′有界; 0≤μ(r,t;y),β(r,t;y),μy(r,t;y),βy(r,t;y),μyy(r,t;y),βyy(r,t;y)≤G; (H4)ω∈L∞(Q), ∀(r,t)∈Q, 0≤ω(r,t)≤G3. (7) 例如: <+∞, a.e于(0,T)内} (8) 是L2(0,T)的非空闭凸子集. 不失一般性, 假设Uad由式(8)确定. 定义1函数p∈L2(Q)称为问题(1)-(4)的弱解, 若∀φ∈Φ0, 满足 其中 (10) 引理1[6]若条件(H1)~(H4)成立, 则系统(P)有唯一解p∈C([0,T];L1(Ω)). 定理1[7]若条件(H1)~(H4)成立, 则系统(P)的C([0,T];L1(Ω))解属于L2(Q)解, 即p∈L2([0,T];L2(0,A))=L2(Q). 证明: 任取v∈Uad,p(v)∈Φ1={φφ∈C([0,T];L1(Ω)),φ(A,t)=φ(0,t)=0}, 用p(v)乘以方程(1)两边, 并在(0,A)上积分, 有 (11) 对式(11)的第一项、 第二项分别利用分部积分法, 并注意到μ(S)的非负性及式(5), 得 (12) 将式(12)两边关于τ在(0,t)上积分,t∈(0,T), 有 (13) 将式(13)右边的第一项运用Hölder不等式, 并由式(2)及假设(H2), 可得 (14) 将式(14)代入式(13), 得 其中C3是与p无关的常数, 即p(r,t)∈L2([0,T];L2(0,A))=L2(Q). 运用定理1的证明方法, 可得: 引理3设(H1)~(H4)成立, 则系统(P)的解p(v)∈L2(Q)关于v是连续的. 证明: 设 (16) 由假设条件(H4)可知0≤J(u)<+∞, 则d∈[0,+∞). 取{vn}⊂Uad, 使得 (17) 由引理2知, 存在{pvn}的子列{pn}, 满足 (18) 其中{vi}⊂{vn},i=n+1,…,kn, 使得 在L2(Q)中. (19) 由式(8)知, {vn}在L2(0,T)中一致有界, 在L2(0,T)中. (20) 在L2(0,T)中. (21) 令 (22) (28) 2) 对式(27)左边第二项, 当n→+∞,i→+∞时, 有 (29) 事实上, 有 3) 对式(27)右边第一项, 当n→+∞,i→+∞时, 有 (30) 事实上, 与式(27)的证明类似, 可以证明 4) 对式(27)右边第二项, 当n→+∞时, 有 (31) 事实上, 有 在式(27)中, 令i→∞,n→∞, 并注意到式(28)~(31), 有 式(32)表明p*为问题(1)-(4)当u=u*,f=0时的解, 即p*=p(u*)为问题(1)-(4)当f=0时的L2(Q)解. 下证u*为性能指标泛函J(v)的最优控制. 定理3设状态函数p(v)是问题(1)-(4)的L2(Q)解, 性能指标泛函J(v)定义如式(6), 容许控制集合Uad由式(8)给定. 序列{vn}是极小化序列,u*∈Uad是式(20)中的极限函数, 即vn→u*在L2(0,T)中弱. 则u*∈Uad即为系统(P)关于问题(7)的最优边界控制, 即 (33) (34) 由式(34)及p*=p(u*), 有p*=pu*, 故有 (35) 即p*为问题(1)-(4)当u=u*时的解,p*=p(u*). 下面证明u*即为最优边界控制, (p*,u*)为最优对, 即证 J(u*)=d. (36) 事实上, 由式(17),(20),(21),(35), 有 即式(36)成立. 下面讨论u*∈U为系统(P)最优边界控制的必要条件, 并确定最优控制的最优性组.记 (37) uλ=u*+λ(u-u*), 0<λ<1, 定理4若u*∈Uad是系统(P)的最优边界控制, 则u*满足如下不等式: ∀u∈Uad. (39) 证明: 设u*∈Uad为最优边界控制, 则由性能指标泛函J(u)的结构式(6), 有 (40) 其中:p(uλ)=p(r,t;uλ);p*(u)=p(r,t;u*); 0<λ<1. 由式(40),(37)和极限的保号性可得 即式(39)成立. 证毕. 为变换式(39), 导入式(38)的伴随状态q(r,t;u)=q(u). (41) 定理5设p(r,t;u)是问题(1)-(4)的广义解, 则伴随问题(41)存在唯一的广义解:q(u)∈L2(Q),Dq(u)∈L2(Q). 证明: 用q(u)乘式(38)的第一式, 并在Q上积分, 得 (42) 在式(42)等号右边对(r,t)进行分部积分, 并结合式(38)和式(41)后3个等式, 得 (43) 由式(43)知, 式(39)等价于 (44) 又由方程(41)知,q(r,t)依赖于p(r,t), 而p(r,t)=p(r,t;u*), 因此式(44)可变为 (45) 综上, 可得本文主要结果: 定理6设p(v)∈L2(Q)是系统(P)的状态,J(v)是由式(6)给出的性能指标,Uad是式(8)表示的容许控制集, 若u*∈Uad为系统(P)关于问题(7)的最优控制, 则u*∈Uad由系统(P)(其中v=u*)、 伴随系统(41)及变分不等式(45)构成的最优性组的联立解{u*,p,q}确定. [1] CAO Chun-ling, CHEN Ren-zhao. Optimal Boundary Control for Time-Varying Population Systems [J]. Journal of Northeast Normal University: Natural Science Edition, 1999(4): 9-13. (曹春玲, 陈任昭. 时变种群系统的最优边界控制 [J]. 东北师大学报: 自然科学版, 1999(4): 9-13.) [2] FU Jun, YAN Shu-kun, LÜ Xian-rui. Penalty Shifting Method on Calculation of Optimal Boundary Control for Time-Varying Population System with Age-Dependence [J]. Journal of Jilin University: Science Edition, 2010, 48(2): 177-182. (付军, 闫淑坤, 吕显瑞. 年龄相关的时变种群系统最优边界控制计算的惩罚移位法 [J]. 吉林大学学报: 理学版, 2010, 48(2): 177-182.) [3] XU Wen-bing, CHEN Ren-zhao. Final State Observation and Boundary Control for a Time-Varying Population System [J]. Journal of Northeast Normal University: Natural Science Edition, 2000, 32(1): 6-9. (徐文兵, 陈任昭. 时变种群系统最终状态观测及边界控制 [J]. 东北师大学报: 自然科学版, 2000, 32(1): 6-9.) [4] HE Ze-rong, ZHU Guang-tian. Optimal Harvesting for a Population System Based on Age Distribution and Weighted Size [J]. Advances in Mathematics, 2006, 35(3): 315-324. (何泽荣, 朱广田. 基于年龄分布和加权总规模的种群系统的最优收获控制 [J]. 数学进展, 2006, 35(3): 315-324.) [5] YE Shan-xi, ZHAO Chun. Optimal Control for a Class of Age-Dependent Population System Based on Weight [J]. Mathematica Applicata, 2007, 20(3): 562-567. (叶山西, 赵春. 一类具有年龄分布和加权的种群系统的最优控制 [J]. 应用数学, 2007, 20(3): 562-567.) [6] CHEN Ren-zhao, LI Jian-quan. Existence and Uniqueness of the Solution for Nonlinear Age-Dependent Time-Varying Population Evolution Equations [J]. Acta Mathematiea Scientia, 2003, 23A(4): 385-400. (陈任昭, 李健全. 与年龄相关的非线性时变种群发展方程解的存在与唯一性 [J]. 数学物理学报, 2003, 23A(4): 385-400.) [7] TIAN Jian-hao, FU Jun. Solution and Continuous Dependency of the Solution for the Boundary Control in a Class of Nonlinear and Weighted Size Population System [J]. Journal of Jilin Normal University: Natural Science Edition, 2009(2): 73-75. (田健豪, 付军. 一类非线性加权种群系统解及其对边界控制的连续相依性 [J]. 吉林师范大学学报: 自然科学版, 2009(2): 73-75.) [8] 黎茨 F, 塞克佛尔维-纳吉 B. 泛函分析讲义 [M]. 庄万, 译. 第二卷. 北京: 科学出版社, 1981: 65-71. [9] 赵义纯. 非线性泛函分析及其应用 [M]. 北京: 高等教育出版社, 1989: 10-11.



1 最优边界控制的存在性

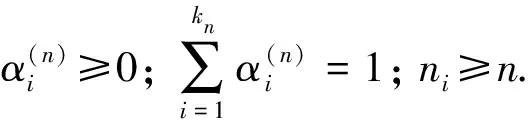
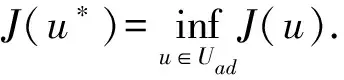







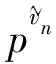
2 控制为最优的必要条件及确定最优控制的最优性组







