单参数电力系统亚临界Hopf分岔控制

李鹏松,陈书吉,吕 雪,盛桂全

(东北电力大学 理学院,吉林 吉林 132012)

分岔控制的主要任务是设计控制器改变非线性系统的分岔特性,获得所需要的系统动力学行为[1].典型的分岔控制包括：将原系统固有的分岔行为延迟； 设计参数值,使之产生新的分岔或改变平衡点的位置； 改变原非线性系统的拓扑结构,改变分岔类型； 改变原系统极限环的多样性、 幅值、 频率等[2].目前控制方法主要有谐波平衡法、 多尺度法、 线性和非线性状态反馈控制法、 规范形方法和Washout-filter(高通滤波器)方法等[3-6].在电力系统分岔分析中,有4种分岔形式和电压稳定性密切相关,分别是鞍结分岔(SNB)、 Hopf分岔(HB)、 奇异诱导分岔(SIB)和极限诱导分岔(LIB).研究表明,电力系统中Hopf分岔可能先于鞍结分岔出现而导致电压失稳或崩溃[7-8].

目前,针对单参数电力系统Hopf分岔的控制研究已取得一些成果,主要是利用高通滤波器方法和线性反馈控制法[1,9].在电力系统中,无功补偿器(SVC)可以输入节点电压的二次项,考虑电力系统的实际物理意义， 本文针对单参数电力系统设计一个二次非线性控制器,以经典的双机三节点电力系统为例,在不改变原系统平衡点及Hopf分岔点的条件下,将亚临界Hopf分岔控制为超临界Hopf分岔,并通过实际算例和仿真分析验证了所设计控制器的实用性和有效性.

1 基本概念

电力系统可抽象为单参数非线性模型

(1)

其中：x为状态变量；μ为可变参数.

Hopf分岔包括超临界Hopf分岔和亚临界Hopf分岔[10],其中: 亚临界Hopf分岔对电压稳定性存在较大危害,使电压稳定域的范围减小,并使系统的载荷能力极大降低;超临界Hopf分岔使电压发生等幅振荡,产生稳定极限环.因此,将亚临界Hopf分岔控制为超临界Hopf分岔具有实际应用价值.

2 经典双机三节点系统的Hopf分岔类型

经典双机三节点电力系统由两台发电机向一负荷供电,等值发电机采用二阶模型,负荷采用第一类动态负荷模型.系统包含4个状态变量: 发电机功角δm、 发电机角频率ω、 负荷点电压幅值u和相角δ.Q1为负荷点的无功功率,是系统的可变参数.描述系统动态特性的状态方程如下：

(2)

其中网络提供给负荷的功率及各参数取值参见文献[11].

根据改进的直接法[12]可求得系统(2)有两个Hopf分岔点H1和H2,且均为亚临界Hopf分岔[13]:

H1：当Q1=10.946 779时,

(δm,ω,δ,u)=(0.310 09,0,0.120 003,1.099 752)；

H2：当Q1=11.406 648时,

(δm,ω,δ,u)=(0.343 44,0,0.136 135,0.942 565).

3 亚临界Hopf分岔控制

考虑分岔点H1,在不改变系统平衡点的条件下,采用二次非线性控制器,这里只对Q1实施控制,结合系统的状态方程(2),控制后的系统为

(3)

其中U=k1(u-ξv)2.显然,该非线性控制器未改变原系统的平衡点.

考虑平衡点H1,取ξ=0.5,则系统在平衡点H1处的Jacobian矩阵所对应的特征值分别为：λ1=-0.5,λ2=-128.651,λ3,4=±3.748i,λ5=-15.367.针对受控系统,先将平衡点H1平移至原点,即

可得受控系统的Poincaré规范形:

(4)

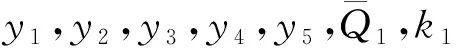
根据Poincaré规范形理论[14],计算系统(4)的Hopf分岔稳定性指标

(5)

其中(下列各式求导均在零点)：

分别计算各特征量,最终得稳定性指标为

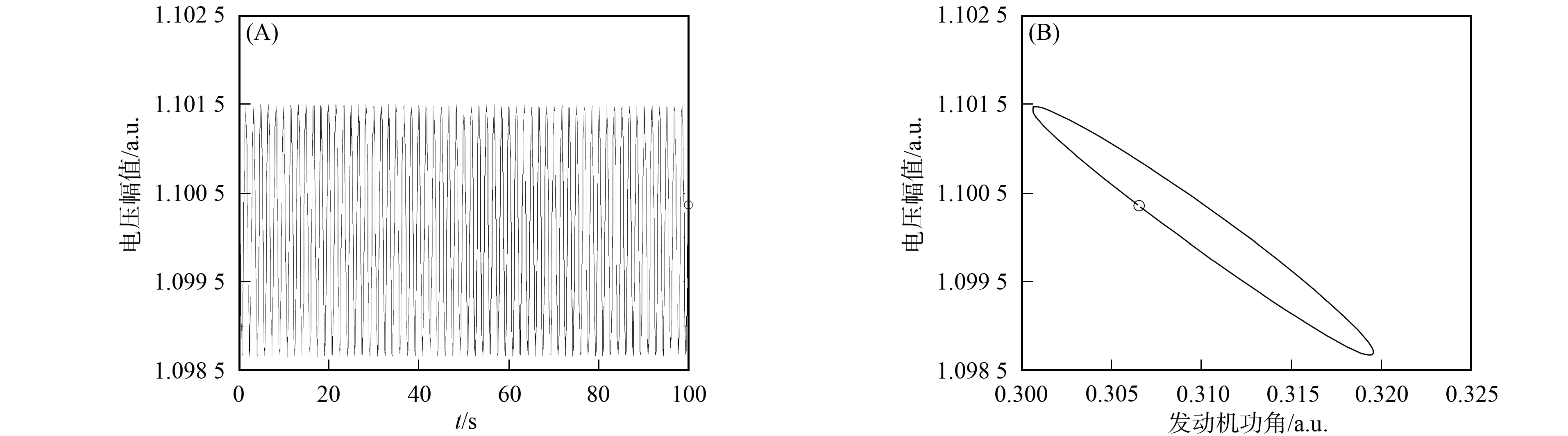
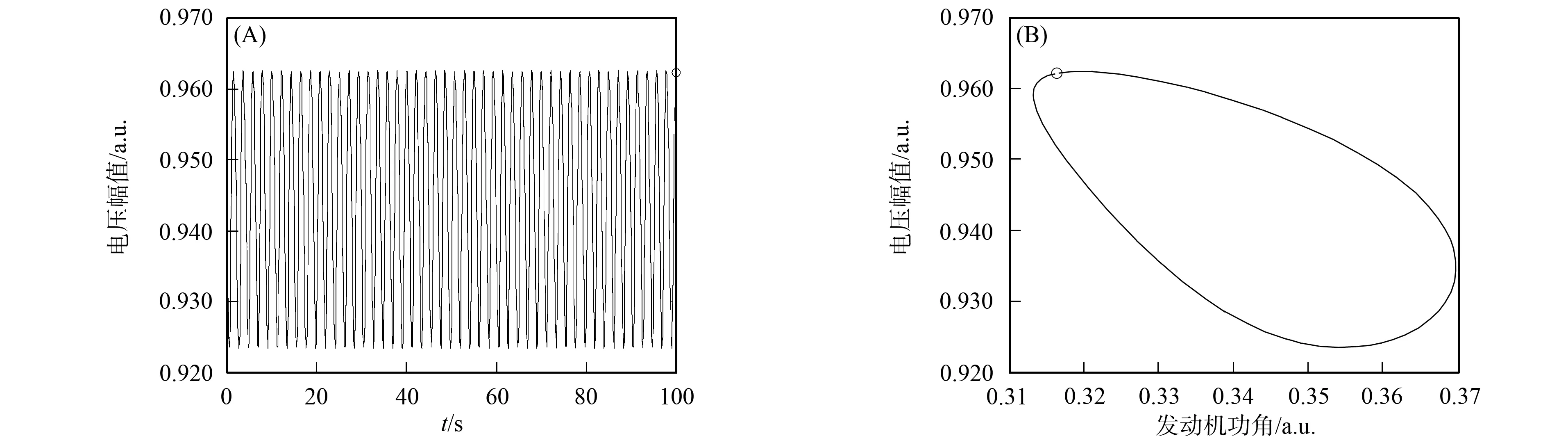
为保证极限环稳定,即β2<0,则19.1

图1为受控系统(3)在第一个Hopf分岔点H1邻域受扰后的Matlab仿真结果.由图1可见,施加控制器后,电压幅值由原来的增幅振荡变为等幅振荡,表明原系统的亚临界Hopf分岔变为超临界Hopf分岔.

图1 当Q1=10.946 777 9时邻域受控系统的电压仿真曲线(A)和δm-u平面相轨迹(B)Fig.1 Simulation curves of voltage (A) and phase trajectory in δm-u plane (B) of controled system for Q1=10.946 777 9

针对第二个分岔点H2,施加与系统(3)相同的控制器,其中U=k2(u-ξv)2.由于H1—H2段系统已失稳,所以分析分岔点H2的分岔类型时需从反方向考虑,即当无功功率Q1由大到小至分岔点H2时的情况.同理,根据式(5)可得Hopf分岔稳定性指标为

为了保证极限环稳定,即β2<0,则k2<0或k2>159.取k2=-50,则β2=-20.385<0,即施加非线性控制器后系统的Hopf分岔点H2由亚临界变为超临界,产生稳定极限环,且该控制器不改变Hopf分岔点H1的类型.

图2为受控系统(3)在第二个Hopf分岔点H2邻域受扰后的Matlab仿真结果.由图2可见,施加控制器后,电压幅值由原来的增幅振荡变为等幅振荡,且产生稳定极限环,表明原系统的亚临界Hopf分岔变为超临界Hopf分岔.

图2 当Q1=11.406 648时邻域受控系统电压的仿真曲线(A)和δm-u的平面相轨迹(B)Fig.2 Simulation curves of voltage (A) and phase trajectory in δm-u plane (B) of controled system for Q1=11.406 648

综上,本文以典型的双机三节点电力系统为例设计了二次非线性控制器,在不改变原系统平衡点及Hopf分岔点的条件下,将其亚临界Hopf分岔控制为超临界Hopf分岔,从而使系统稳定,并通过数值模拟验证了所设计控制器的有效性.本文的结论适用于含单参数电力系统的亚临界Hopf分岔控制.

[1] MA You-jie,LI Xiao-shuang,ZHOU Xue-song,et al.Control of Dynamic Bifurcation in Power System Based on Washout-Filter [J].Power System Protection and Control,2011,39(23)：54-59.(马幼捷,李小双,周雪松,等.基于Washout-filter方法的电力系统动分岔控制 [J].电力系统保护与控制,2011,39(23)：54-59.)

[2] FANG Yang-wang.Comprehensive Theoretical Study of Nonlinear Control Systems [D].Xi’an：Xi’an Jiaotong University,1997.(方洋旺.非线性控制系统的综合理论研究 [D].西安：西安交通大学,1997.)

[3] CUI Yan,LIU Su-hua,GE Xiao-ling.Amplitude Control of Limit Cycle from Hopf Bifurcation in the Langford System [J].Acta Physica Sinica,2012,61(10)：100202.(崔岩,刘素华,葛晓陵.Langford系统Hopf分岔极限环幅值控制 [J].物理学报,2012,61(10)：100202.)

[4] LIU Su-hua,ZHAO Cheng-gang,TANG Jia-shi,et al.Hopf Bifurcation Analysis and Amplitude Control of Limit Cycle in the Qi System [J].Journal of Dynamics and Control,2008,6(2)：141-145.(刘素华,赵成刚,唐驾时,等.Qi系统的Hopf分叉分析与幅值控制 [J].动力学与控制学报,2008,6(2)：141-145.)

[5] Chen Z,Yu P.Controlling and Anti-controlling Hopf Bifurcations in Discrete Maps Using Polynomial Functions [J].Chaos,Solitons and Fractals,2005,26(4)：1231-1248.

[6] AN Yi-chun， ZHANG Qing-ling， ZHANG Yan， et al.Control Based on Wash-Out-Filter for Hopf Bifurcation of Nonlinear Systems [J].Journal of Northeastern University：Natural Science， 2008， 29(10)：1381-1384． (安祎春， 张庆灵， 张艳， 等． 基于Wash-Out-Filter方法控制非线性系统Hopf分岔 [J]． 东北大学学报：自然科学版， 2008， 29(10)：1381-1384．)

[7] JING Zhu-jun,XU Da-shun,CHANG Yu， et al.Bifurcations,Chaos,and System Collapse in a Three Node Power System [J].International Journal of Electrical Power and Energy Systems,2003,25(6)：443-461.

[8] GU Wei,Milano F,JIANG Ping,et al.Hopf Bifurcations Induced by SVC Controllers：A Didactic Example [J].Electric Power Systems Research,2007,77(3/4)：234-240.

[9] LIU Ji-guang,WANG Hai-yang,ZHONG Li-jun,et al.Hopf Bifurcation Control of Voltage Stability in Wind Power System [J].Journal of Jilin University: Science Edition,2013,51(1)：111-115.(刘继广,王海洋,钟利军,等.风电系统电压稳定性的Hopf分岔控制仿真 [J].吉林大学学报: 理学版,2013,51(1)：111-115.)

[10] ZHAO Xing-yong,ZHANG Xiu-bin,SU Xiao-lin.Voltage Stability Studies and Bifurcation Theory in Power Systems [J].Transactions of China Electrotechnical Society,2008,23(2)：87-95.(赵兴勇,张秀彬,苏小林.电力系统电压稳定性研究与分岔理论 [J].电工技术学报,2008,23(2)：87-95.)

[11] LI Peng-song,CHEN Shu-ji,LÜ Xue.Hopf Bifurcation Type of Power System Based on Analytic Methods [J].Journal of Jilin University: Science Edition,2012,50(4)：701-704.(李鹏松,陈书吉,吕雪.基于解析方法电力系统的Hopf分岔类型 [J].吉林大学学报: 理学版,2012,50(4)：701-704.)

[12] Roose D,Hlavacek V.A Direct Method for the Computation of Hopf Bifurcation Points [J].SIAM Journal on Applied Mathematics,1985,45(6)：879-894.

[13] 彭志炜,胡国根,韩祯祥.基于分叉理论的电力系统电压稳定性分析 [M].北京：中国电力出版社,2005.

[14] Hassard B D,Kazarinoff N D,Wan Y H.Theory and Applications of Hopf Bifurcation [M].Cambridge: Cambridge University Press,1981.