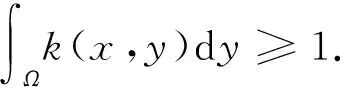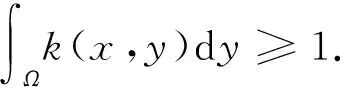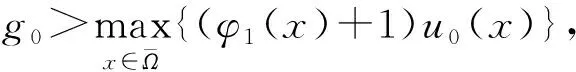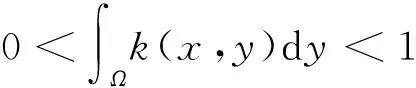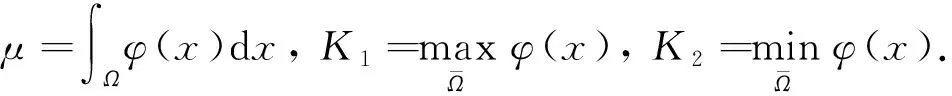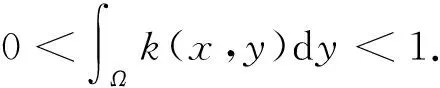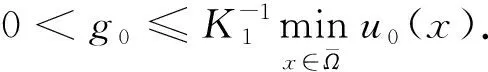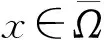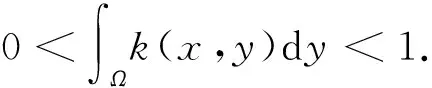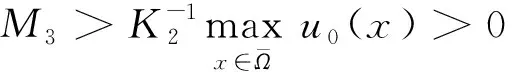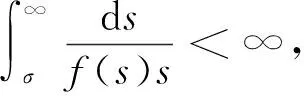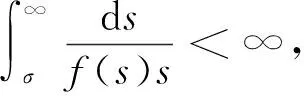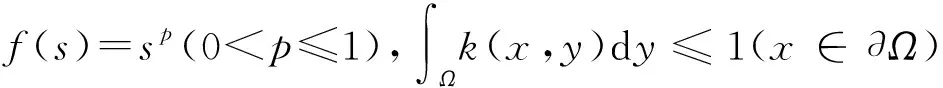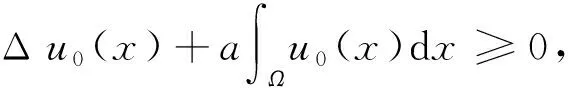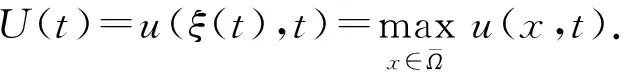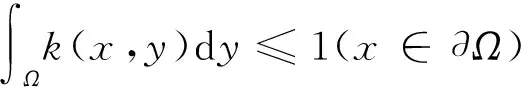一类具非局部边界条件的拟线性抛物方程解的整体存在与爆破
孟繁慧,高文杰
(1.长春金融高等专科学校,长春 130028;2.吉林大学 数学学院,长春 130012)
0 引 言
考虑如下具非局部边界条件和内部吸收项的拟线性抛物型方程:
(1)
其中:Ω是N(N≥1)中具有光滑边界∂Ω的有界区域;a为正常数;u0(x),f(s)和k(x,y)分别满足如下假设条件:
(H1)f∈C([0,∞))∩C1((0,∞)),满足f(0)≥0,f′(s)>0,s∈(0,∞);


许多物理、 化学或生物种群动力学现象都可以用具非局部源的抛物型方程描述.例如,文献[1]指出非局部反应项能更精确地描述可压缩活性气体的燃烧过程.当f(s)=sp(0 (2) 在某种特殊情形下解的整体存在和衰减性质;文献[6]给出了问题(2)在k(x,y)≥0,g(x,u)=cu(其中c是一个没有任何限制的常数)情形下解的一个整体上界和特殊情形时边界值的衰减性质; 文献[7]建立了问题(2)的比较原理,并对一般形式的g(x,u)证明了问题(2)古典解的局部存在性,对g(x,u)=c(x)u的特殊情形,证明了解的整体存在性和指数增长性质.当g(x,u)关于u的增长超线性时,问题(2)的解可能在有限时刻爆破.特别地,文献[8]在g(x,u)=g(u)情形下讨论了问题(2),用上下解的方法给出了此时问题正解在有限时刻爆破的充分条件,此外,还给出了当g(u)=up及g(u)=eu时解的爆破速率估计. 考虑如下具非局部边界条件和局部反应项的多孔介质方程: (3) 其中:m,p>1为常数;初值u0(x)和权函数k(x,y)满足与问题(1)相同的假设.文献[9]给出了问题(3)存在整体解的充分必要条件,并得到了解的爆破速率估计.文献[10-16]研究了具非局部边界条件的抛物方程或方程组,得到了一些有意义的结果. 上述研究表明,问题(2),(3)解的增长或衰减性质依赖于g(x,u)的增长,这与具齐次边界条件的半线性方程解的性质相似.另一方面,由于非局部边值的存在性,解的渐近性质也依赖于权函数k(x,y).基于此,本文研究问题(1)正古典解的渐近性质,考虑非线性扩散、 非局部项、 吸收项和非局部边界条件对解渐近性质的综合影响. 则称v(x,t)是问题(1)的一个下解.改变定义1中不等号的方向可以得到上解的定义.如果函数v(x,t)既是问题(1)的一个上解又是一个下解,则称其为问题(1)的一个(古典)解. 问题(1)古典解的局部存在性可以用标准压缩映像不动点定理得到[7,17].正古典解的唯一性可由下述引理推出. (4) 证明: 考虑如下常微分方程初值问题: (5) 证明: 先构造问题(1)的一个整体存在且下方有界的上解.记λ1和φ1(x)>0(x∈Ω)分别是如下特征值问题的第一特征值和相应的特征函数: -Δφ=λφ,x∈Ω;φ(x)=0,x∈∂Ω. (6) (7) Δv=div(v) 可得 (9) 另一方面,由式(7)可知,对任意的x∈∂Ω都有 (10) (11) 证明: 通过构造一个下方有界且爆破的下解完成证明.考虑如下Cauchy问题: (12) (14) (15) 式(13)~(15)表明,v(x,t)是问题(1)的一个下方有界的爆破下解.再次应用命题1可知u(x,t)也在有限时刻爆破.证毕. 还可证明当非局部项的系数a适当大时,对任意满足假设(H3)的k(x,y),问题(1)的解都在有限时刻爆破.为此,记ψ(x)为下述椭圆问题的唯一正解: -Δψ(x)=1,x∈Ω;ψ(x)=0,x∈∂Ω. (16) 证明: 考虑如下齐次Dirichlet边值问题: (17) (H4) 存在常数δ>0,使得对任意的x∈Ω,有 这里δ是满足δ+1≥a|Ω|的正常数. 引理2假设(H2)~(H4)成立,且u(x,t)在T时刻爆破,则对任意的(x,t)∈Ω×[0,T),有Δu≤0. 设w(x,t)=Δu(x,t),则由式(1)可知对任意的(x,t)∈Ω×(0,T),有 wt=upΔw+2pup-1u·w+pu-1utw+p(p-1)u-2ut-2pup-1-upw. (18) 注意到ut≥0,0 wt-upΔw-2pup-1u·w≤pu-1utw-upw, (x,t)∈Ω×(0,T). (19) 最后由假设条件(H4)可知 w(x,0)=Δu0(x)≤0,x∈Ω. (21) 结合式(19)~(21)及引理1可得w(x,t)=Δu≤0,(x,t)∈Ω×(0,T).证毕. 引理3假设(H2)~(H4)成立,且u(x,t)在T时刻爆破.则存在正常数C1,使得U(t)≥C1(T-t)-1/p. 证明: 由方程(1)、U(t)的定义及引理2可得 U′(t)≤a|Ω|Up+1(t). (22) 对式(22)在(t,T)上积分并注意到当t→T时U(t)→∞,得U(t)≥C1(T-t)-1/p,这里C1=(ap|Ω|)-1/p.证毕. 引理4假设(H2)~(H4)成立,且u(x,t)在T时刻爆破.则有ut≥δup+1,(x,t)∈Ω×(0,T). 证明: 记J(x,t)=ut-δup+1.直接计算可得 由Young不等式和Hölder不等式可知,对任意的正常数θ,都有 对任意的(x,t)∈∂Ω×(0,T),有 将式(27)代入式(26)得 (28) 此外,假设(H4)蕴含 J(x,0)≥(δ-δ)u0(x)p+1=0,x∈Ω. (29) 对ut≥δup+1在区间(t,T)上直接积分可得 u(x,t)≤C2(T-t)-1/p, (x,t)∈Ω×(0,T), (30) 这里C2=(δp)-1/p.综合U(t)≥C1(T-t)-1/p和式(30),得: [1] Bebernes J,Bressan A,Lacey A.Total Blow-up versus Single Point Blow-up [J].J Differen Equat,1988,73(1): 30-44. [3] Carlson D E.Linear Thermoelasticity,Encyclopedia of Physics [M].Berlin: Springer,1972. [4] Day W A.A Decreasing Property of Solutions of Parabolic Equations with Applications to Thermoelasticity [J].Quart Appl Math,1983,40(4): 468-475. [5] Friedman A.Monotonic Decay of Solutions of Parabolic Equations with Nonlocal Boundary Conditions [J].Quart Appl Math,1986,44(3): 401-407. [6] Seo S.Global Existence and Decreasing Property of Boundary Values of Solutions to Parabolic Equations with Nonlocal Boundary Conditions [J].Pacific J Math,2000,193(1): 219-226. [7] Deng K.Comparison Principle for Some Nonlocal Problems [J].Quart Appl Math,1992,50(3): 517-522. [8] Seo S.Blow-up of Solutions to Heat Equations with Nonlocal Boundary Conditions [J].Kobe J Math,1996,13(2): 123-132. [9] WANG Yu-lan,MU Chun-lai,XIANG Zhao-yin.Blowup of Solutions to a Porous Medium Equation with Nonlocal Boundary Condition [J].Appl Math Comput,2007,192(2): 579-585. [10] Carl S,Lakshmikantham V.Generalized Quasilinearization Method for Reaction-Diffusion Equations under Nonlinear and Nonlocal Flux Conditions [J].J Math Anal Appl,2002,271(1): 182-205. [11] HAN Yu-zhu,GAO Wen-jie.Complete Classification of Solutions to a Parabolic Equation with Nonlocal Boundary Condition [J].Dynamics Cont Discrete Impulsive Systems Series A,2012,19(5): 599-613. [12] LIN Zhi-gui,LIU Yu-rong.Uniform Blowup Profile for Diffusion Equations with Nonlocal Source and Nonlocal Boundary [J].Acta Math Sci,2004,24B(3): 443-450. [13] Pao C V.Dynamics of Reaction-Diffusion Equations with Nonlocal Boundary Conditions [J].Quart Appl Math,1995,53(1): 173-186. [14] Pao C V.Asymptotic Behavior of Solutions of Reaction-Diffusion Equations with Nonlocal Boundary Conditions [J].J Comput Appl Math,1998,88(1): 225-238. [15] Pao C V.Numerical Solutions of Reaction-Diffusion Equations with Nonlocal Boundary Conditions [J].J Comput Appl Math,2001,136(1/2): 227-243. [16] YIN Hong-ming.On a Class of Parabolic Equations with Nonlocal Boundary Conditions [J].J Math Anal Appl,2004,294(2): 712-728. [17] Friedman A.Partial Differential Equations of Parabolic Type [M].New York: Prentice-Hall,1964. [18] CHEN You-peng,LIU Li-hua.Global Blow-up for a Localized Nonlinear Parabolic Equation with a Nonlocal Boundary Condition [J].J Math Anal Appl,2011,384(2): 421-430. [19] HAN Yu-zhu,GAO Wen-jie.A Degenerate Parabolic Equation with a Nonlocal Source and an Absorption Term [J].Applicable Analysis,2010,89(12): 1917-1930.1 比较原理

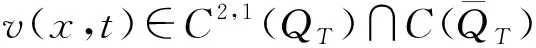
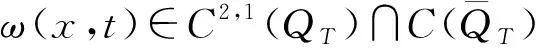

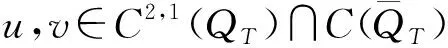
2 解的整体存在和爆破