同伦内点法求解多目标规划问题
赵 雪,杨月婷,张树功
(1.北华大学 数学与统计学院,吉林 吉林 132013; 2.吉林大学 数学学院,长春 130012)
0 引言与预备知识
同伦方法是一种大范围收敛方法[1-2],其作为一种全局收敛方法目前已引起人们广泛关注,并成为数值解决互补问题、 变分不等式和不动点等问题的重要工具[3-6].文献[7]定义了正独立映射的概念,给出了比法锥条件更弱的拟法锥条件,并给出了修正的组合同伦方程.本文把同伦内点方法运用到多目标规划问题中,通过引入拟法锥条件,削弱了对约束区域非凸性条件的限制,从而扩大了组合同伦内点法的求解范围.
考虑多目标规划问题:

(1)
其中f=(f1,f2,…,fp)T:n→p和g=(g1,g2,…,gm)T:n→m均为二次连续可微函数.
令Ω={x∈n|gi(x)≤0,i=1,2,…,m}表示可行域,Ω0={x∈n|gi(x)<0}表示严格可行域,∂Ω=ΩΩ0表示可行解集的边界.记

定义2令U⊂n是一个开集,φ:U→p是Cα(α>max{0,n-p})映射.如果Range[∂φ(x)/∂x]=p,∀x∈φ-1(y),则称y∈n是φ的一个正则值.
引理1(参数化Sard定理)[8]令V⊂n,U⊂m是开集,且φ:V×U→k是一个Cα映射,其中α>max{0,m-k}.如果0∈k是φ的一个正则值,则对于几乎所有的a∈V,0是φa=φ(a,·)的一个正则值.
引理2(逆映像定理)[8]令φ:U⊂n→p是一个Cα(α>max{0,n-p})映射.如果0是φ的一个正则值,则φ-1(0)由一些(n-p)-维Cα流形构成.
引理3(一维光滑流形的分类定理)[8]一个一维光滑流形同胚于一个单位圆或一个单位区间.
假设条件:
(H1)Ω是非空连通的有界闭集合,Ω0非空;
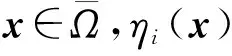

1 同伦路径的存在性及全局收敛性
构造如下组合同伦方程:
(2)
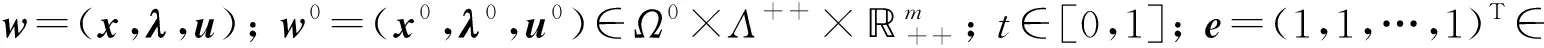

证明: 由同伦方程(2),得
(3)

由于tk→t*∈[0,1],λk>0,故当k→∞时,式(3)左边的第二部分趋于无穷,而其余两部分是有界的,矛盾.从而λ的分量有界.

证明:令DH(w,w0,t)表示H(w,w0,t)的Jacobi矩阵,
其中:I是单位矩阵;U0=diag(u0).


(1-tk)(f(x)(xk)λk+g(x)(xk)uk+tkη(xk)(uk)2)+tk(xk-x0)=0,
Ukg(x)(xk)-tkU0g(x)(x0)=0.
当k→∞时,有下列几种情形发生:
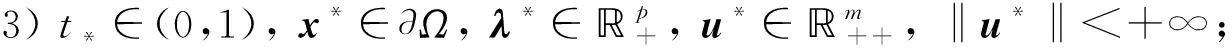
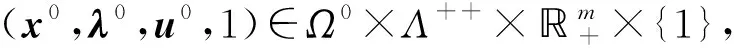
(1-tk)(f(x)(xk)λk+g(xk)uk+tkη(xk)(uk)2)+tk(xk-x0)=0.
(4)
当t*=1时,式(4)可改写为
令k→∞,有
从而
其中αi∈+,得这与拟法锥条件矛盾.
当t*∈[0,1)时,有

2 数值算例
例1
(6)
由约束函数(6)构成的可行域满足拟法锥条件.取t0=1,初始点为(3.000 0,0.000 0),可得x*=(3.755 2,-0.869 0)T.
例2
(7)
由约束函数(7)构成的可行域满足拟法锥条件.取t0=1,初始点为(-0.500 0,-0.100 0),可得x*=(-1.000 0,-0.006 2)T.
[1] Kellogg R B,Li T Y,Yorke J A.A Constructive Proof the Brouwer Fixed-Point Theorem and Computational Results [J].SIAM J Numer Analysis,1976,13(4): 473-483.
[2] Chow S N,Mallet-Paret J,York J A.Finding Zeroes of Maps: Homotopy Methods That Are Constructive with Probability One [J].Math Comput,1978,32: 887-899.
[3] Gowda M S.On the Extended Linear Complementarity Problem [J].Mathematical Programming,1996,72: 33-50.
[4] ZHAO Xue,ZHANG Shu-gong,LIU Qing-huai.A Combined Homotopy Interior Point Method for the Linear Complementarity Problem [J].Journal of Information and Computational Science,2010,7(7): 1589-1594.
[5] FAN Xiao-na,YU Bo.A Smoothing Homotopy Method for Solving Variational Inequalities [J].Nonlinear Analysis: Theory,Methods &Applications,2009,10(1): 211-219.
[6] SU Meng-long,LIU Zhen-xin.Modified Homotopy Method to Solve Fixed Points of Sel-Mapping in a Broader Class of Nonconvex Sets [J].Applied Numerical Mathematics,2008,58(3): 236-248.
[7] LIU Qing-huai,YU Bo,FENG Guo-chen.An Interior Point Path-Following Method for Non-convex Programming with Quasi-normal Cone Condition [J].Advances in Mathematics,2000,19(4): 281-282.
[8] 张筑生.微分拓扑新讲 [M].北京:北京大学出版社,2002.

