六自由度振动试验系统运动极限*

张步云，陈怀海，贺旭东，郭家骅

（1.南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016）

（2.上海宇航系统工程研究所 上海，201108）

引 言

在实验室条件下用振动台进行振动测试试验是对产品在运输、使用环境中经受振动环境的最佳人工模拟［1］。单轴振动试验技术在工程领域应用广泛，局限性也很明显。文献［2－3］指出单轴振动试验无法完全复现外场故障，加大量级的补偿措施易导致试件过试验或过设计，难以实现不同振动方向载荷的准确迭加。贺旭东［4］指出在对大型试件进行振动试验时，单轴振动台无法提供足够的推力，难以达到规定的试验量级，且单点激励不利于实现振动分布的均匀性，使应力和位移分布不够合理。Freeman［5］指出通过单轴振动试验的设备无法承受多维的外场振动环境。事实上，从严格意义来说，产品在使用过程中的振动环境大都是多自由度的，单轴振动试验难以准确描述产品的真实工况。

从20世纪60年代开始，研究重点转移到多轴振动系统领域，并取得一系列进展。Whiteman等［6－7］研究了多维振动试验方法，指出多轴振动试验能有效减少试验时间且提供更真实的应力分布情况。美国的Wyle实验室、MTS公司和Team公司等都开始研究多轴振动环境试验技术，且应用到实际产品的生产中。Wyle实验室为Hill空军基地研制的三轴向六自由度电动振动系统是目前较先进的电动式多轴振动系统［8］。关广丰等［9－10］就六自由度液压振动试验系统的控制策略进行了理论和试验研究。严侠等［11］以三轴向六自由度液压振动台系统为典型被控对象，建立了三轴六自由度液压振动台随机振动控制仿真系统。陈建秋等［12－13］对六自由度地震模拟振动台的控制系统进行了研究。这些研究多以多轴液压振动系统为主。

在振动试验中关心的是多轴振动系统的试验能力，尤其是六自由度电动振动系统。若已知振动系统的相关参数，求得台面的最大运动能力（即能达到的最大位移或最大加速度）是研究人员关心的问题。另一方面，给定一定的试验条件，振动台能否达到这样的指标是试验能否成功的关键。笔者根据斯图尔特平台模型［14－16］的分析方法，以六自由度电动振动系统台面的运动极限问题进行建模研究，建立各振动台与台面之间的位移关系，为多轴振动系统试验的实际应用提供理论依据。

1 振动系统几何模型

在实际振动环境中，大部分产品有6个自由度的运动，其中：3个平动自由度分别为沿x轴、y轴和z轴的移动；3个转动自由度为绕轴x旋转的Rx、绕y轴旋转的Ry和绕z轴旋转的Rz。图1为六自由度振动简化模型。

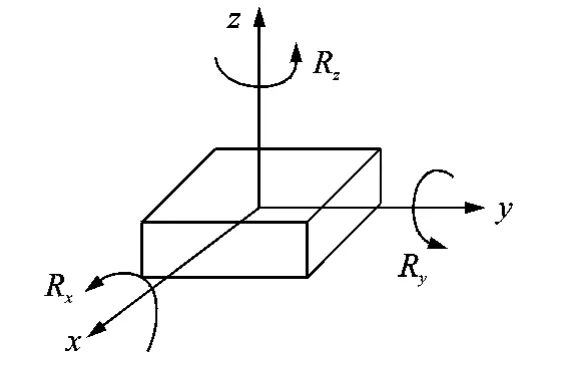
图1 六自由度振动模型图

在具有8个独立的单轴振动台的六自由度振动系统中，每个自由度的响应都是由8个振动台共同激励产生的［17］。图2为美国Hill空军基地SVIC中心的多台多轴（MEMA）系统，由2个x向振动台、2个y向振动台、4个z向振动台和一个振动台面组成［8］。本研究以此系统为研究对象。

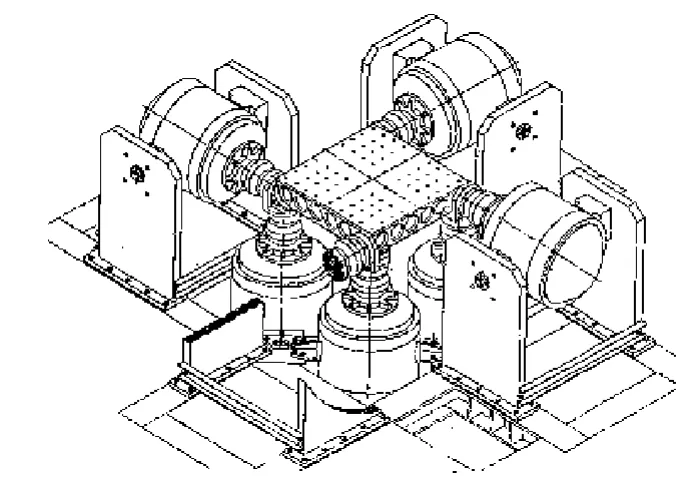
图2 美国Hill空军基地多台多轴系统

根据斯图尔特平台系统的相关理论，在多轴电动振动系统中引入类似分析方法，建立如图3所示的振动系统模型。该振动系统由振动台面和8个独立单轴振动台组成，振动台用序号＃1，＃2，…，＃8表示。＃1和＃2表示x向的振动台，＃3和＃4表示y向的振动台，＃5～＃8表示z向的4个振动台。为了消除不同轴向运动之间耦合关联，该系统通过连接试验台面和振动台动圈的静压球形接头来实现机械解耦。振动台的下铰点为具有4个自由度的球铰联接，固定在系统底座。振动台的上铰点与台面相连，传递作用力。

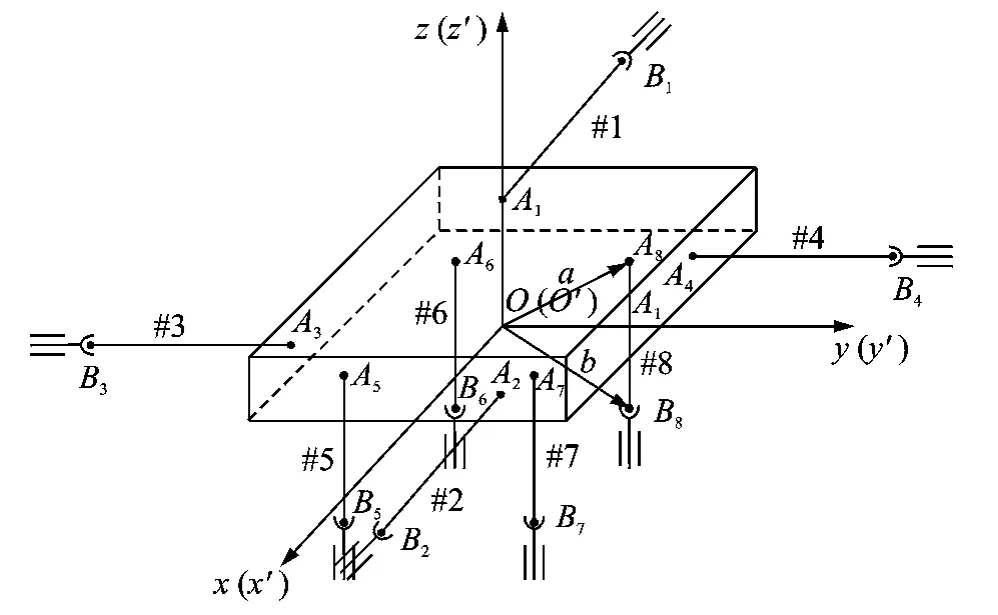
图3 八振动台多轴系统几何模型

为准确计算振动台的轴向伸缩与台面运动之间的关系，以＃1到＃4振动台与台面的连接点所在面的几何中心为原点建立两个空间直角坐标系。其中：一个坐标系O－xyz固连于大地，称为静坐标系S；另一坐标系O′－x′y′z′固连于台面，称为动坐标系M。

8个振动台的下铰点在坐标系S中的坐标不变，上铰点在动坐标系M中的坐标不变。台面处于中位时两坐标系重合［9］。原点O到振动台下铰点Bi的向量为bi＝［bixbiybiz］T，i＝1，2，…，8，原点O′到上铰点Aj的向量为aj＝［ajxajyajz］T，j＝1，2，…，8。

2 振动系统运动分析

2.1 各振动台试验能力

分析各振动台试验能力，即在已知振动台面运动的情况下求得各振动台轴向的伸缩位移。一般称此类问题为振动系统反解问题。求得各振动台的轴向伸缩位移，结合已知振动台参数，便可判断振动系统的试验能力。如图3所示，振动台面的位姿x可以表示为

其中：t3×1为平动位移坐标向量，即原点O到O′的向量表示为转动坐标向量分别为绕 x轴、y轴和z轴的转角。

用此3个参数可以计算出静坐标系到动坐标系的转动传递矩阵R［15］为

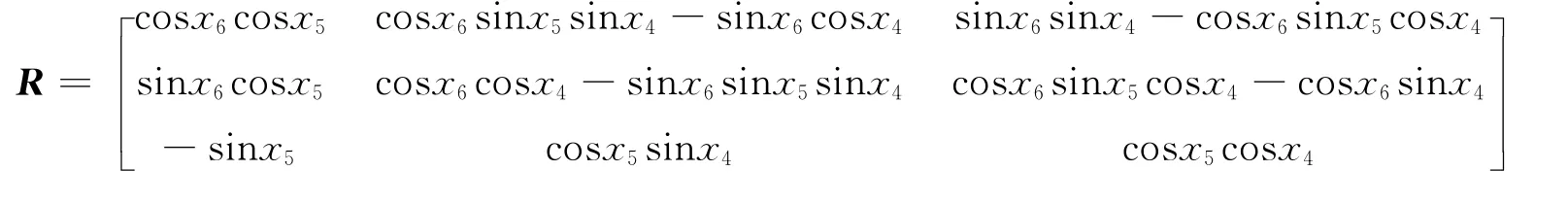
台面的运动速度可以表示为

因为台面的运动是8个振动台共同激励的结果，下面探求振动台的轴向伸缩位移与台面的位姿之间的关系。第i个振动台上、下铰点间向量可表示为li，有

其中：li为一个3×1维的向量，它表示振动台的位置。

其中：｜li｜为台面运动时振动台的长度。振动台的轴向伸缩位移Δli为

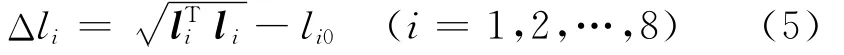
其中：li0为无台面运动时第i个振动台的轴向长度。

由式（5）可知，振动台的轴向伸缩位移Δli可以表示成台面6个自由度的函数。若知振动台面的运动，可由式（5）求出各振动台应该具备的试验能力。

2.2 振动台面极限运动

振动台面运动分析相对各振动台轴向位移的求解难度较大，国内外学者研究了分析振动台面运动的方法［18－20］。在实际工程中仅仅求得振动台面的运动是不够的。振动系统的最大试验能力在振动环境试验中具有重要的实际意义，每一个轴向运动或转动能达到怎样的极限位置是值得考虑的问题。

由式（3）和式（5）可以得到一组非线性方程组为

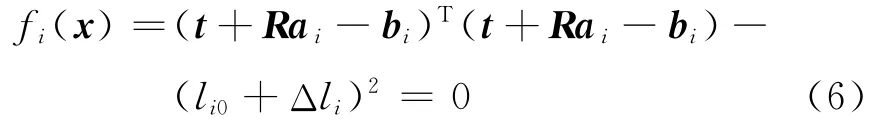
其中：i＝128

当已知各振动台的伸缩位移Δli时，式（6）可以写成

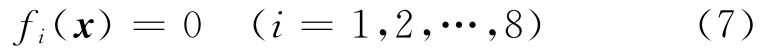
该方程组有8个方程，6个未知数。对于每组给定的振动台轴向位移 Δli（i＝1，2，…，8），运用Newton－Raphson算法或QR分解法都可得到相应的台面运动x。每个振动台的轴向位移都在一定的范围内，即

当振动台轴向位移不同时台面的运动也不同。分析振动台面的运动极限即找出一组最优的振动台轴向位移，使得振动台面某一自由度的平动位移或转角达到最大值，该值即表示振动台最大的试验能力。此时可以将振动台的轴向位移视为自变量，振动台面的运动即为轴向位移的函数。式（7）可以写为

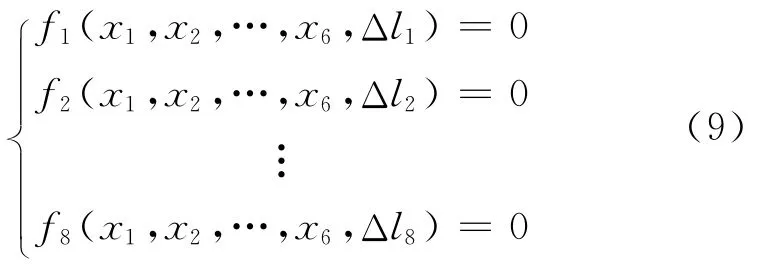
其中：Δli（i＝1，2，…，8）为变量，其定义域为式（8）。

台面的每个自由度运动都可表示为Δli（i＝1，2，…，8）的函数，即

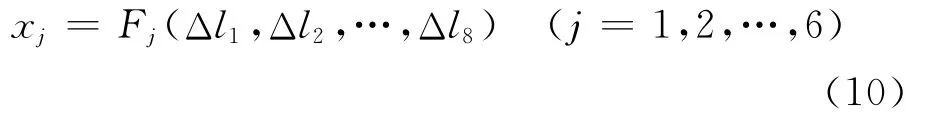
3 算 例

3.1 参数设定

当台面运动时，第i个振动台的轴向伸缩位移Δli是以台面6个自由度为自变量的函数。若是单轴振动系统，振动台的伸缩位移即为台面的运动位移。在多轴振动系统中，由于不同轴向的振动之间存在着机械耦合，每个振动台的运动不仅产生轴向位移，还对其他轴向的运动产生牵连作用，所以当单个振动台的位移达到最大值时，试验台面的位移并不一定达到最大值。表1为多轴振动系统相关参数，计算其台面的位移范围，可以得到上、下各铰点在静坐标系中的坐标，如表2和表3所示。

表1 多轴振动台参数设定 mm

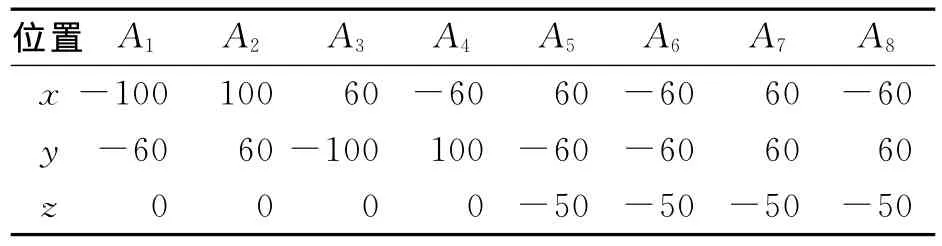
表2 各振动台上铰点的坐标向量 mm

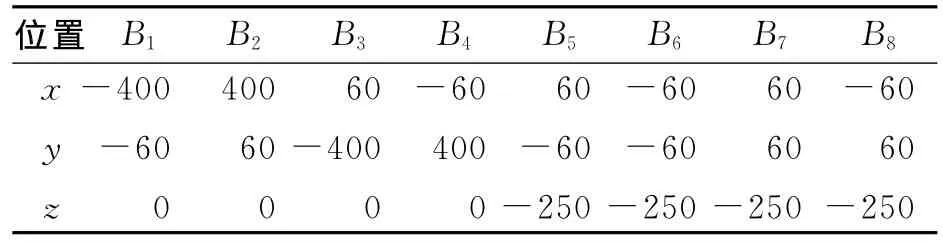
表3 各振动台下铰点的坐标向量 mm

3.2 计算结果

向量aj和向量bi的值分别为Aj和Bi的坐标值。可以计算出振动台的伸缩位移为何值时台面的位移达到最大，如表4所示。可以看出，当某一轴向振动台伸缩位移达到最大值时，该向的台面运动达到最大值；但台面运动的最大值并不仅由这一轴向的振动台提供，其他各向振动台都有位移贡献。由表4得到该振动系统平动的运动范围为［－25mm，25mm］，绕x轴和y轴转动角范围为［－20.805°，20.805°］，绕z轴 转 动 角 范 围 为 ［－18.168°，18.168°］，此为该振动系统的试验能力。

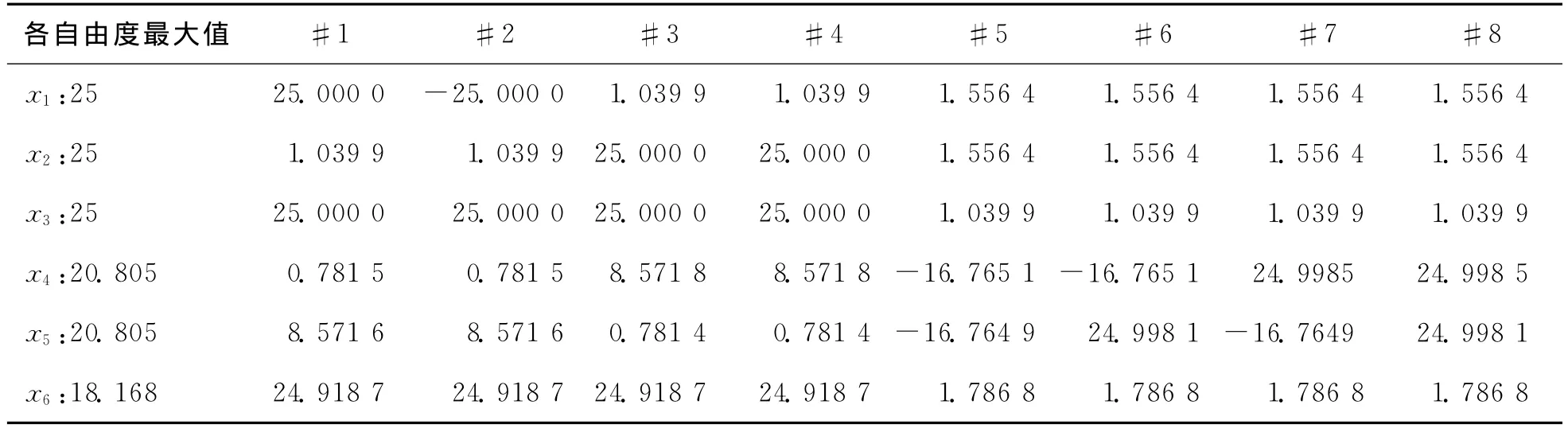
表4 各振动台位移与台面极限位移 mm

另一方面，若已知试验条件，可以求得振动台应具有的试验能力。例如，要求台面的x轴向位移达到20mm，同时绕x轴转动角度达到18°，可以得到各振动台的轴向位移应满足的条件如表5所示。可以看出，要达到设定的试验条件，需要振动台的最大轴向位移为22.244 0mm，设计的振动台完全能够满足此试验要求。

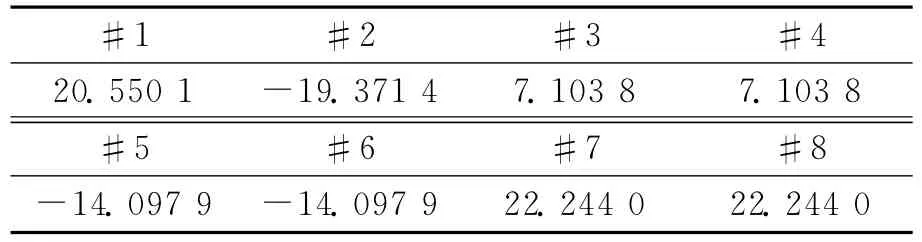
表5 x1＝20mm，x4＝18°时各振动台的轴向位移mm

4 结束语

在六自由度振动试验系统中，不同自由度之间存在机械耦合，每个轴向的平动或绕轴的转动都是由所有振动台共同作用形成的。笔者在机械解耦的基础上计算试验系统的最大试验能力，在实际试验实施中有着重要的应用。笔者仅对台面的位移和振动台位移之间的关系进行了探讨，速度与加速度之间的关系并未涉及。在多轴振动试验中，具有一定质量的试件会对振动台产生倾覆力矩，振动台和台面之间的运动关系更为复杂，这些问题需要进一步研究。

［1］ Davis T.MIMO control system－a new ear in shaker control［J］.Sound and Vibration，2006，40（1）：6－9.

［2］ 夏益霖.多轴振动环境试验的技术、设备和应用［J］.导弹与航天运载技术，1996，6：48－55.Xia Yilin.The technology，equipment and application of multi－axis vibration environment testing［J］.Missiles and Space Vehicles，1996，6：48－55.（in Chinese）

［3］ Harman C.Multi－axis vibration reduces test time［J］.Evauluation Engineering，2006，45（6）：44－47.

［4］ 贺旭东.多输入多输出振动试验控制系统的理论、算法及实现［D］.南京：南京航空航天大学，2006.

［5］ Freeman M T.3－Axis vibration test system simulates real world［J］.Test Engineering and Management，1990，12：10－14.

［6］ Whiteman W E，Berman M S.Inadequacies in uniaxial stress screen vibration testing［J］.Journal of the IEST，2001，44：20－23.

［7］ Whiteman W E.Fatigue failure results for multi－axial versus uniaxial stress vibration testing［J］.Shock and Vibration，2002，9：319－328.

［8］ Chen M，Wilson D R.The new tri－axial shock and vi－bration test system at hill air force base［J］.Journal of Institute of Environmental Sciences and Technology，1998，41（2）：27－32.

［9］ 关广丰.液压驱动六自由度振动试验系统控制策略研究［D］.哈尔滨：哈尔滨工业大学，2007.

［10］关广丰，王海涛，熊伟.6自由度液压振动台运动学分析及控制策略［J］.振动、测试与诊断，2011，31（1）：89－93.Guan Guangfeng，Wang Haitao，Xiong Wei.Kinematic analysis and control strategy of 6－DOF hydraulic vibration table［J］.Journal of Vibration，Measurement＆ Diagnosis，2011，31（1）：89－93.（in Chinese）

［11］严侠，牛宝良，朱长春.三轴六自由度液压振动台随机振动控制分析与仿真［J］.机床与液压，2007，35（10）：165－191.Yan Xia，Niu Baoliang，Zhu Changchun.MIMO random vibration control simulation in the three axis－six DOF shaking table［J］.Machine Tool ＆ Hydraulics，2007，35（10）：165－191.（in Chinese）

［12］陈建秋.六自由度模拟地震振动台台面控制原理研究［J］.广州大学学报：自然科学版，2006，5（3）：75－79.Chen Jianqiu.Analysis of 6－DOF and table control of seismic simulation system［J］.Journal of Guangzhou University：Natural Science Edition，2006，5（3）：75－79.（in Chinese）

［13］陈建秋，任珉，杨泽群.模拟地震振动台台面补偿技术分析［J］.广州大学学报：自然科学版，2005，4（1）：74－77.Chen Jianqiu，Ren Min，Yang Zequn.Analysis of compensation technology of seismic simulation system［J］.Journal of Guangzhou University：Natural Science Edition，2005，4（1）：74－77.（in Chinese）

［14］Koebebakker S.Model based control of a flight simulator motion system［D］.Delft：Delft University of Technology，2001.

［15］马建明.飞行器模拟液压Stewart平台奇异位形分析及其解决方法研究［D］.哈尔滨：哈尔滨工业大学，2010.

［16］Bhaskar D，Mruthyunjaya T S.The stewart platform manipulator：a review［J］.Mechanism and Machine Theory，2000（35）：15－40.

［17］Underwood M A，Keller T.Applying coordinate transfor－mations to multi－DOF shaker control［J］.Sound and Vibration，2006，1：2－8.

［18］Lin W，Griffis M，Duffy J.Forward displacement analysis of the 4－4stewart platforms［J］.Journal of Mechanical Design，1992，114：444－450.

［19］Raghavan M.The stewart platform of general geometry has 40configurations［J］.Journal of Mechanical Design，1993，115（2）：277－282.

［20］Ku D M.Direct displacement analysis of a stewart platform mechanism ［J］. Mechanism and Machine Theory，1999，34：453－465.