单输入多自由度系统自然激励技术的解析格式*

钟军军，董 聪

（清华大学土木工程系 北京，100084）

引 言

随着社会经济的高速发展，大型复杂工程结构得到了广泛应用。为确保其安全运营，建立结构健康监测系统十分必要。对大型复杂工程结构健康监测系统而言，在环境激励下提取结构模态参数是需要解决的关键问题之一［1－3］。自然激励技术（natural excitation technique，简称 NExT）［4－5］为环境激励下结构模态参数的提取提供了一条新的途径［6－10］，但其工作存在两个问题：单输入白噪声激励下结构系统位移响应的互相关函数仅给出了最终形式，未给出关键参数——衰减正弦函数的相位角和幅值的解析表达式；对单个动力荷载恰好作用在振型节点时可能出现的现象没有分析和解释。这些问题的解决对于NExT理论的完善及应用具有重要意义。笔者推导了单输入白噪声激励下多自由度结构系统位移响应互相关函数的解析表达，分析阐释了单个动力荷载恰好作用在振型节点时的现象。

1 位移响应的互相关函数

结构系统的动力方程为

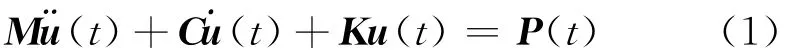
结构任意两个自由度a和b上位移响应的互相关函数为

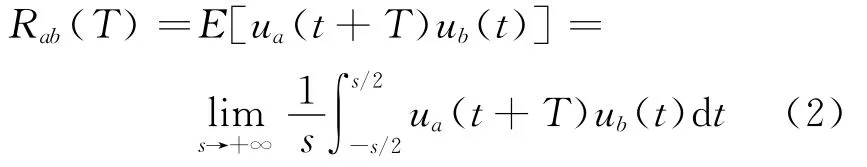
其中：E［·］表示数学期望。

由式（2）可知，Rab（T）与t无关，是一个以时间差T为自变量的函数。

单输入白噪声激励情况下［4－5］有

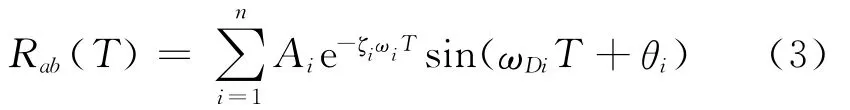
其中：ζi，ωi和ωDi分别为结构系统第i阶模态的模态阻尼比、固有圆频率和有阻尼固有圆频率。

由式（3）可知，位移互相关函数具有与结构系统单位脉冲响应函数相似的结构，它可用于时域模态参数识别。

2 相位角θi和幅值Ai的解析表达

结构系统的位移响应u（t）可分解为

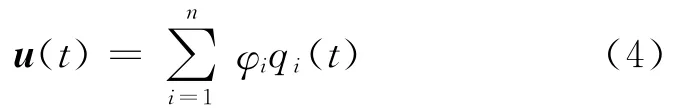
其中：φi为结构系统的第i阶振型向量；qi（t）为φi对应的正规坐标。

采用经典阻尼假设，即

用φiT左乘式（1），同时将式（4）代入式（1），可将系统动力方程解耦得到一系列单自由度系统动力方程

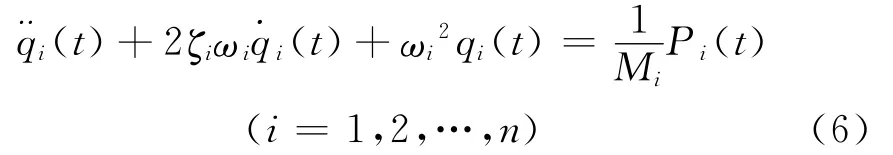
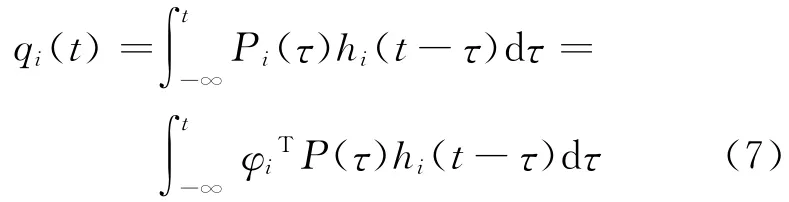
其中

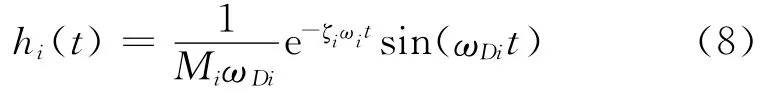
为单自由度系统的单位脉冲响应函数；ωDi＝

将式（7）代入式（4），得

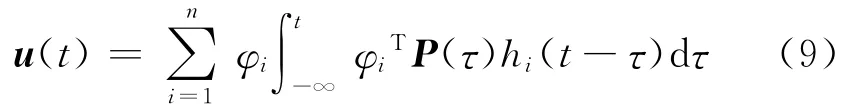
设单输入荷载pk（t）作用在第k自由度上，即P（t）的第k个元素pk（t）非零，其他元素为零，则

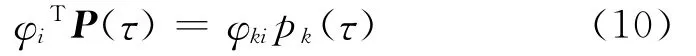
由式（9）可得结构任意自由度a上的位移响应为

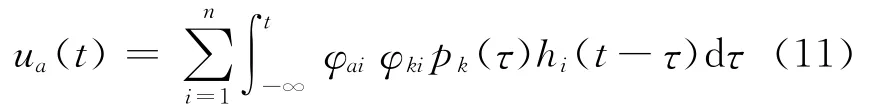
其中：ua（t）和φai分别为向量u（t）和φi的第a个元素。

当pk（t）为单位脉冲荷载时，多自由度系统的位移响应为

假定荷载pk（t）为零均值白噪声，即整个频率范围内具有均匀功率谱密度函数的随机过程，其自相关函数为

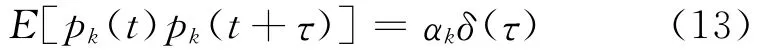
其中：αk为与荷载的均匀功率谱密度函数值有关的一个正常数；δ（·）为Dirac－δ函数。

将式（11）代入式（2），得

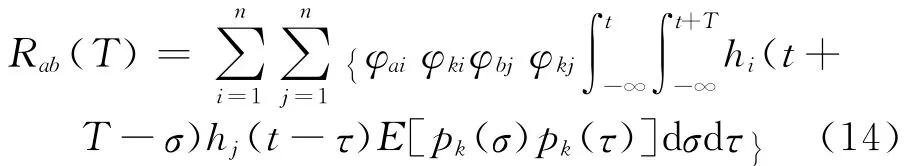
由式（13）可知

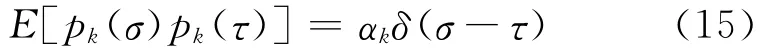
将式（15）代入式（14），得

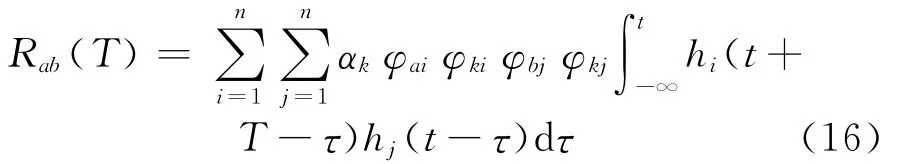
令λ＝t－τ，则式（16）变换为

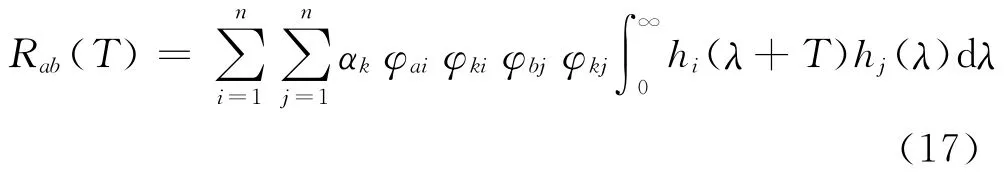
由式（8）可得

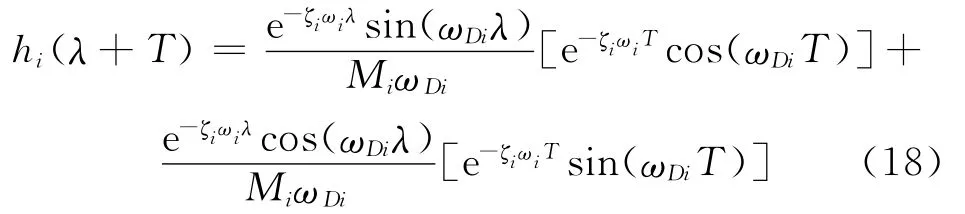
将式（8），（18）代入式（17），整理得到

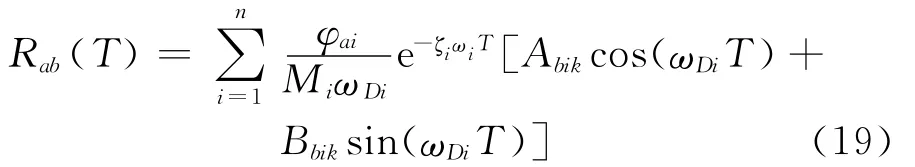
其中

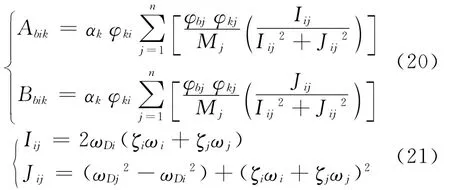
由式（20）～（21）可知，Abik和Bbik均为与T 无关，而只与模态参数有关的常数，根据系数Bbik的取值分为以下两类情况讨论。

1）当Bbik＝0时，由式（19）得

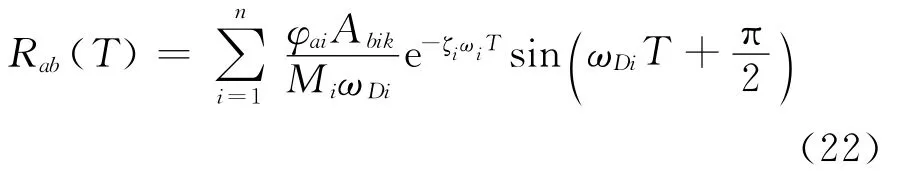
对比式（3）和式（22）可知

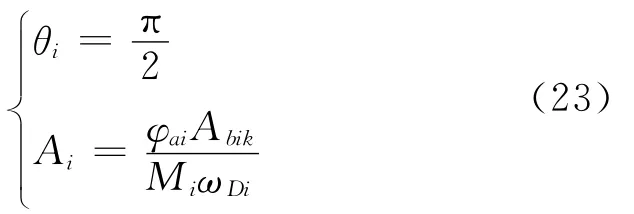
2）当Bbik≠0时，定义

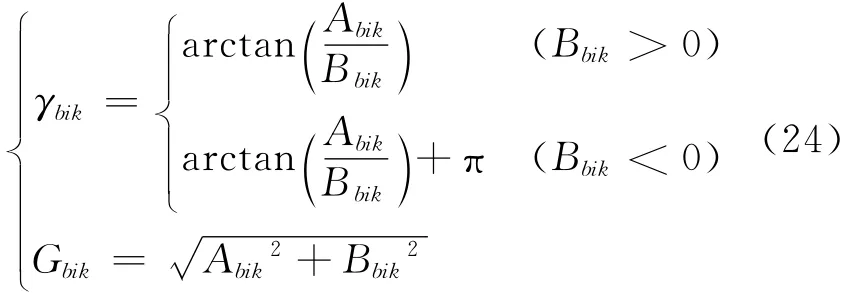
可得

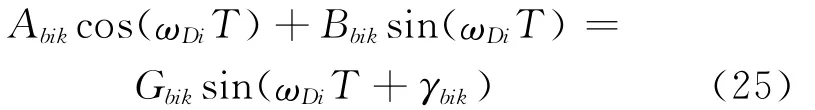
将式（25）代入式（19），得到

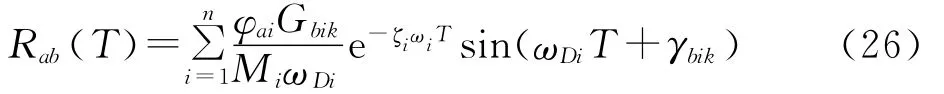
对比式（3）和式（26）可知

综合以上两种情况，将式（24）代入式（27），得到θi和Ai的完整解析表达为

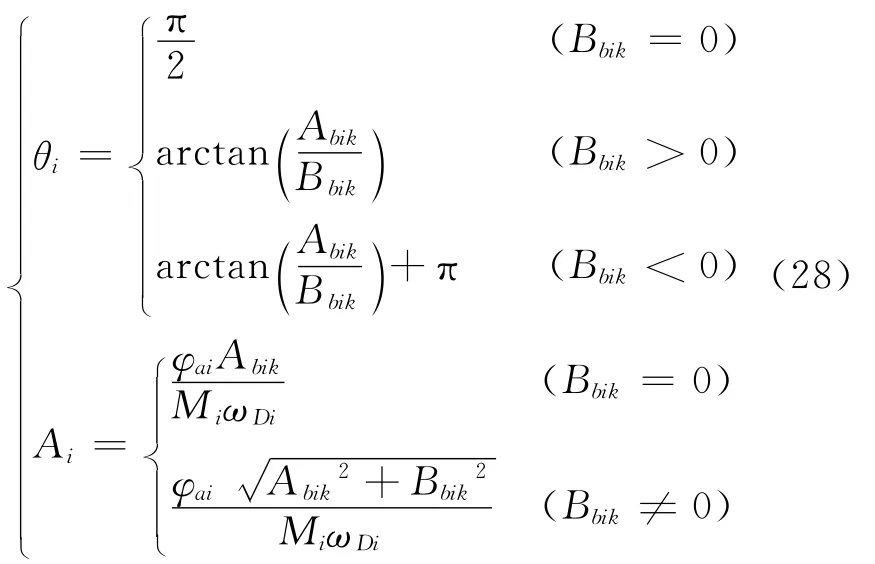
其中：Abik和Bbik详见式（20）。

3 动力荷载作用在振型节点的情况

φki＝0表示动力荷载pk（t）恰好作用在结构系统第i阶振型的某个节点，由式（7）可得

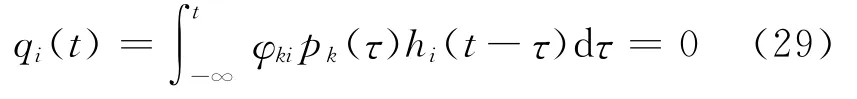
此时结构系统位移响应中第i阶振型的贡献为零，即荷载无法激励起第i阶模态，导致该阶模态在位移响应中得不到反映。

根据式（28）可知此时有

当单输入动力荷载恰好作用在结构系统某阶振型节点时，结构任意两个自由度位移响应的互相关函数中将不含有频率值等于该阶模态有阻尼固有频率的简谐成分，即该阶模态的相关信息在互相关函数中得不到反映。在这一点上，互相关函数与位移响应的性质是一致的。由式（30）可知，若结构系统某阶振型的所有非节点处均无外荷载作用，则该阶模态不会被激励起来。

4 结 论

1）推导了单输入白噪声激励下多自由度系统位移响应的互相关函数，证明它可表达成一系列衰减正弦函数之和，且各个组分正弦函数的频率恰好等于结构系统各阶模态的有阻尼固有圆频率，给出了各个衰减正弦函数的相位角θi和幅值Ai的解析表达。

2）当单输入动力荷载恰好作用在系统某阶位移模态的节点时，任意两自由度位移响应的互相关函数中将不含有频率值等于该阶模态有阻尼固有频率的简谐成分，即该阶模态的信息在互相关函数中得不到反映。若结构系统某阶振型的所有非节点处均无外荷载作用，则该阶模态不会被激励起来。

［1］ Farrar C R，Worden K.An introduction to structural health monitoring［J］.Philosophical Transactions of the Royal Society A，2007，365（1851）：303－315.

［2］ Vistasp M K，Farhad A.Structural health monitoring of civil infrastructure systems［M］.Cambridge CB21 6AH，UK：Woodhead Publishing Limited and CRC Press LLC，2009：213－259.

［3］ 刘宗政，陈恳，郭隆德，等.基于环境激励的桥梁模态参数识别［J］.振动、测试与诊断，2010，30（3）：300－303.Liu Zongzheng，Chen Ken，Guo Longde，et al.Modal parameter identification of a bridge under ambient excitation［J］.Journal of Vibration，Measurement ＆Diagnosis，2010，30（3）：300－303.（in Chinese）

［4］ James G H，Carne T G，Lauffer J P.The natural excitation technique（NExT）for modal parameter extraction from operating wind turbines［R］.Albuquerque，NM：Sandia National Labratories，1993.

［5］ James G H，Carne T G，Lauffer J P.The natural excitation technique（NExT）for modal parameter extraction from operating structures［J］.The International Journal of Analytical and Experimental Modal Analysis，1995，10（4）：260－277.

［6］ James G H，Carne T G，Mayes R L.Modal parameter extraction from large operating structures using ambient excitation［R］.Albuquerque，NM：Sandia National Labratories，1995.

［7］ Carne T G，James G H.The inception of OMA in the development of modal testing technology for wind turbines［J］.Mechanical Systems and Signal Processing，2010，24（5）：1213－1226.

［8］ Farrar C R，James G H.System identification from ambient vibration measurements on a bridge［J］.Journal of Sound and Vibration，1997，205（1）：1－18.

［9］ Liu W，Gao W C，Sun Y.Application of modal identification methods to spatial structure using field measurement data［J］.Journal of Vibration and Acoustics－Transactions of the ASME，2009，131（3）：1－10.

［10］Brownjohn J M W，Magalhaes F，Caetano E，et al.Ambient vibration re－testing and operational modal analysis of the Humber Bridge［J］.Engineering Structures，2010，32（8）：2003－2018.