斜辊式矫直机矫直钢管的压扁量等参数的研究
左雁冰,张 超,黄维勇,陈 锋,常 瑜,何 潜,刘 杰
(中国重型机械研究院股份公司,陕西 西安 710032)
0 前言
通常对斜辊矫直技术没有对板带等其他矫直技术的研究更充分,有的技术及工艺参数的研究尚属空白。究其原因,往往是使用者对钢管矫直技术的认识进入一个误区,认为矫直质量与矫直精度等技术指标仅仅取决于设备本身。这种认识是片面的:产品的矫直质量及精度等技术指标,除了与设备辊列布置及调整控制系统等硬件有关外,还与工艺参数的调整设定有密切关系。对于高精矫直而言,一些工艺参数(如倾角α、压扁量δ、反弯量fc压扁力p以及矫直辊的尺寸精度和表面质量等)甚至对矫直精度起到决定性的作用,这一点已经被实践所证明。
为了对矫直技术有一个完整准确的认识,作者将几个主要的工艺参数问题,在前人的基础上进行分析讨论,以供参考。
1 压扁力及压扁量的确定
1.1 单位接触长度的压扁力p和总压扁力P
可以认为用两个相对单位接触长度的辊子作用于单位长度的圆环,鉴于上下左右的对称性,可以计算圆环的四分之一,如图1所示。
由于各方向的对称性,多余约束的未知量只剩下静不定弯矩M0,则内力方程按曲梁表示为
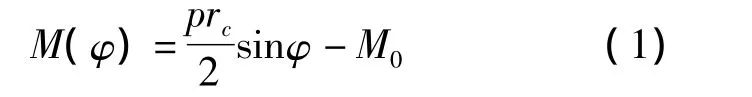
按卡氏定理的变形协调条件,即在A-A断面处转角等于零,则有
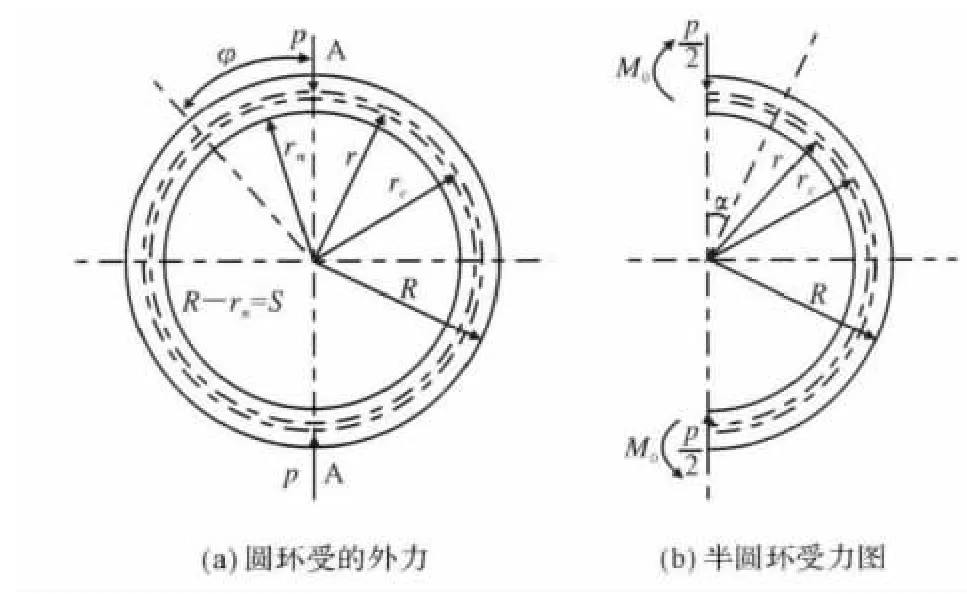
图1 计算简图Fig.1 Calculation sketch
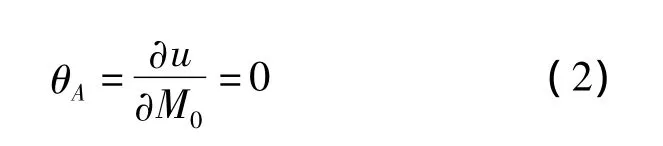
将式(1)代入式(2),则
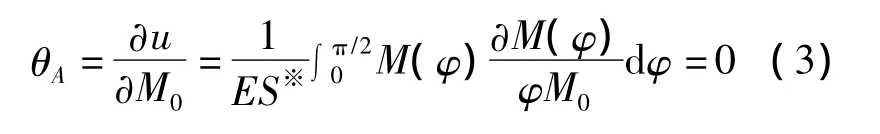
计算得
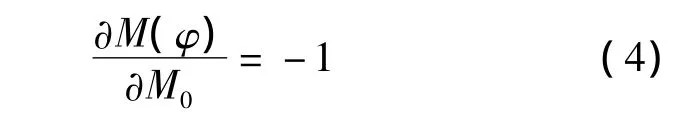
代入式(3)中得出
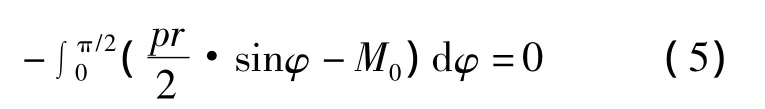
积分(5)式解出
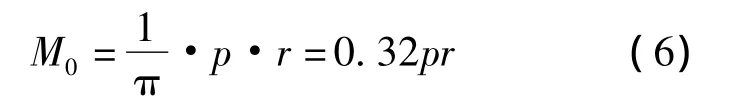
代入(1)式
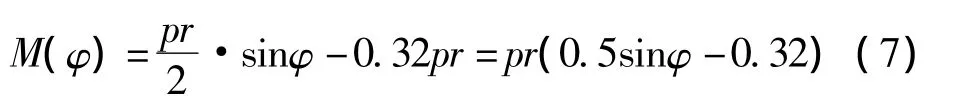
环弯矩图如图2所示。
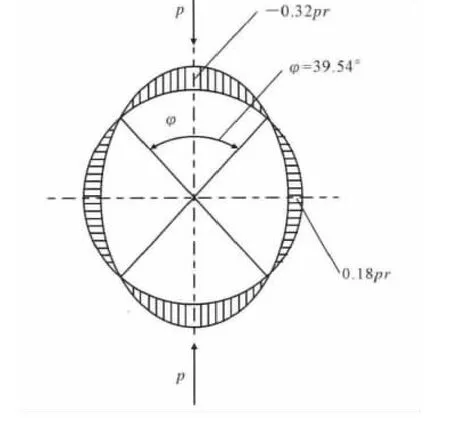
图2 圆环受压弯矩图Fig.2 Bend moment on the borne circle
图1,图2符号的意义:rc为圆环(钢管)几何中心半径;r为平面弯曲曲梁形心半径;S为钢管壁厚;S※曲梁弯曲时静距;R为圆环(钢管)外半径;rn为圆环(钢管)内半径;p为圆环单位长度压力;P为圆环总接触长度的总压力。
1.2 压扁量δ的计算
在矫直过程中,矫直辊与圆环(钢管)的接触倾斜一个角度β,其数值不大,可以认为β=0。对于曲梁变形(δ/2),按以下关系计算:
利用卡氏定理,计算弯矩对p/2的偏导数
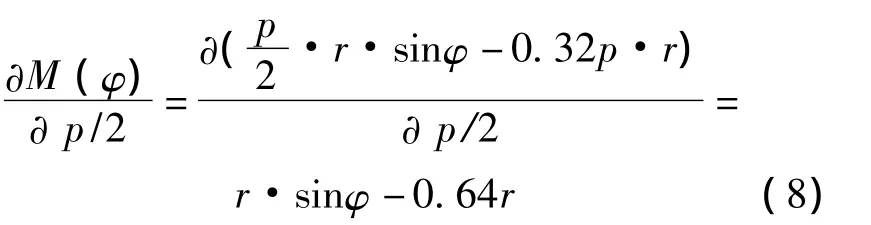
压扁量δ表达为
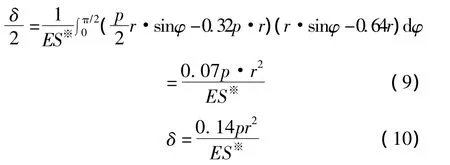
1.3 压扁力
曲梁弯曲应力表达式为

(11)式与(7)式联解
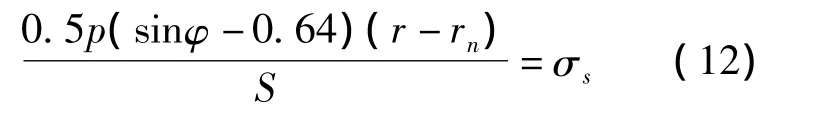

总的压扁力按下式计算
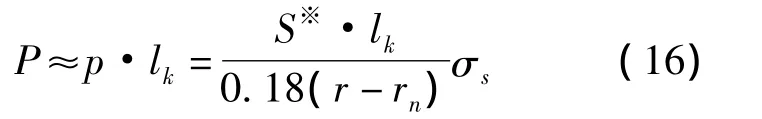
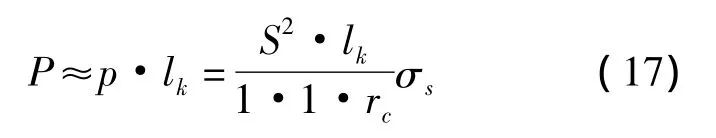
按英国Bronx公司以Pauk理论推出的计算公式为
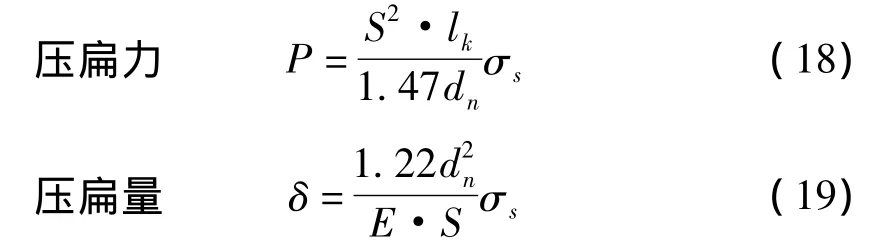
在此列出(18)、(19)式供参考。
2 对计算结果的分析
2.1 压扁力的计算比较
按以下条件计算:
接触长度lk=320 mm、σ=500 MPa、R=50 mm,边缘处达到屈服极限计算结果见表1。

表1 压扁力计算结果比较Tab.1 Comparison of the calculated press flat force results N
通过数值计算表明,按曲梁计算和按直梁计算其计算结果数值差约在10% ~40%。而对于钢管外径R=50 mm规格,壁厚可能由3 mm增至16 mm。因而不能用直梁计算(对厚壁管D/S=6时)。Pauk计算方法经分析是用直梁计算,所以计算的压扁力偏小,特别是所列计算方法没有考虑外区的影响。经生产实践表明,在矫直过程中没有发生钢管被压坏的情况。只有在高速矫直时,钢管头部才有可能被压坏。对薄壁管计算的压扁力都小。这是建立在线接触的情况。实际上存在小的接触面。因此也具有一定的抗压能力。
2.2 关于压扁量问题
用式(13)计算出的单位长度的压扁力p比用式(9)或式(10)计算出的压扁量δ小,这正是管子未被矫坏的原因;说明计算得出的值具有合理性,只有在调节出错时,或者压扁量给大时才会出现压坏管子的情况。特别是加大压扁量不能提高矫直精度,这种做法不仅矫不直,还会在矫直过程中会因为δ大而出现缺陷。要么矫坏产品,要么降低矫直的直线精度,不仅破坏表面状态,还降低尺寸精度。通过压扁方法达到矫直目的的观点是不适宜的。所以不推荐这种方法,特别对高精度矫直更是如此。
3 结论
在理论研究的基础上,中国重型机械研究院股份公司近年来为宝钢、鞍钢、太钢等国内各大钢管厂设计成套供货了几十台钢管矫直机。经实际使用的情况分析,采用曲梁法计算的压扁量是合适的。一般来说,压扁量δ选取在1%~1.3%范围内为好。
[1]曲洪德,徐素文,汪恩辉.18~65mm十一辊高精度管材矫直机研究[J].重型机械,1997(4):5-7.
[2]崔甫.矫直机械与矫直原理[M].北京:机械工业出版社,2002.
[3]A·M马斯基列逊.管材矫直机[M].北京:机械工业出版社,1979.

