VAI结晶器振动参数的研究
刘云峰,刘 才,张玉娟,陈化顺,刘 珺
(1.燕山大学 机械工程学院,河北 秦皇岛 066004;2.张家口职业技术学院,河北 张家口 07500)
0 前言
应用连铸结晶器振动反向控制模型能在提高拉速时增大保护渣消耗量,由于在此过程中负滑动时间近似为常数,因此可以保证获得良好的铸坯表面质量。振痕深度、保护渣消耗量与钢种的化学成分及所使用的保护渣、结晶器振动参数等有关,在其他条件相同的情况下,详细研究振动参数对振痕深度、保护渣消耗的影响具有重要意义,可为振动参数的优化、连铸工艺的优化提供理论依据。
1 奥钢联结晶器振动反向控制模型及参数介绍
奥钢联结晶器振动采用反向控制模型,即在一定拉速范围内振幅是拉速的增函数,频率是拉速的减函数,可实现反向正弦与非正弦振动[1],其控制模型及振动波形如图1所示。此控制模型可确保负滑动时间在预先设计的整个拉速范围内近似为一常数,有利于改善铸坯表面质量;而正滑动时间在整个拉速范围内会随着拉速的递增而变大,有利于增加保护渣的消耗量。总之,采用反向控制模型既可使低拉速时的振痕浅,又能保证高拉速时的保护渣消耗量,可达到更好的冶金效果,大大减少铸坯的粘结、漏钢事故。
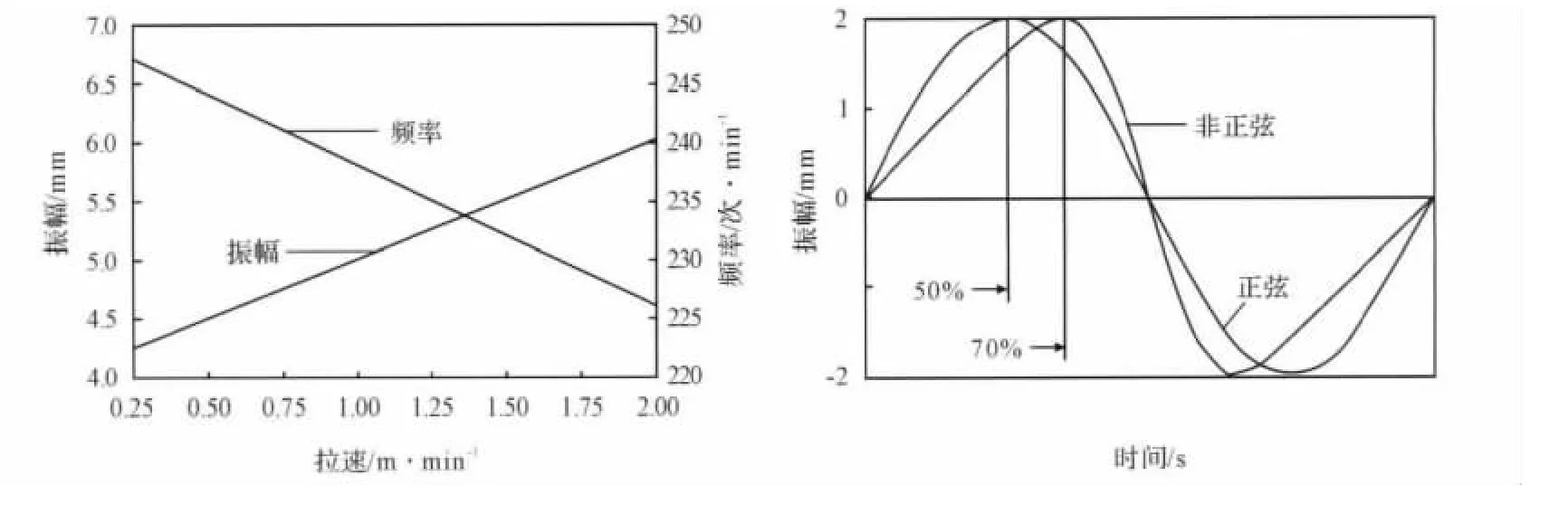
图1 反向控制模型及其振动波形Fig.1 Inverse control model and oscillation wave form
奥钢联提供的反向振动模型如下
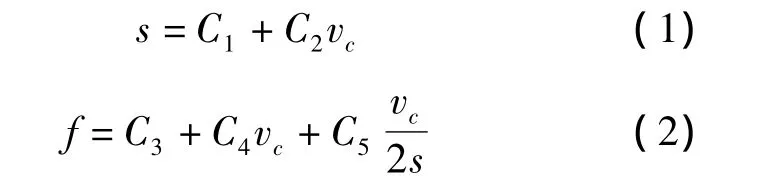
式中,s为振幅,mm;f为频率,min-1;v为拉坯速度,m/min;C1为零拉坯速度下的振幅,mm;C2为振幅/拉坯速度因数,10-3min;C3为零拉坯速度下的频率,次/min;C4为频率/拉坯速度因数,次/m;C5为负滑动因数;C6为非正弦因数。
C6的取值范围为0.5~0.7,其取值决定了结晶器振动方式为正弦或非正弦振动。当C6=0.5时,振动方式为正弦振动,当0.5<C6≤0.7时,振动方式为非正弦振动。奥钢联提供的非正弦因数C6与波形偏斜率α的函数关系式为
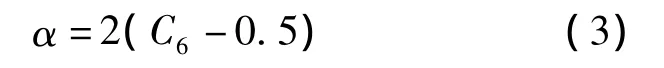
根据文献[2],非正弦振动的负滑动时间、正滑动时间、振动周期的函数表达式分别为
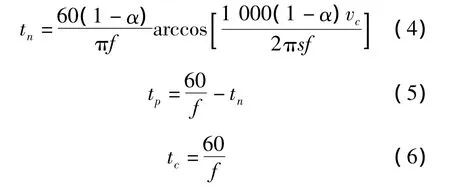
式中,tn为负滑动时间,s;tp为正滑动时间,s;tc为振动周期,s。
将式(3)代入式(4)、(5)可得到用C参数表示的正、负滑动时间如下
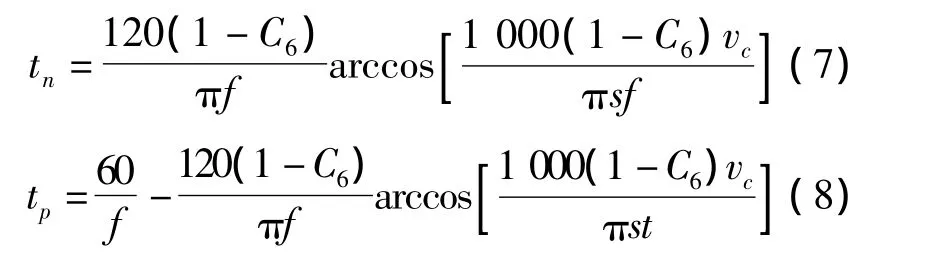
2 振痕间距与振痕深度
振痕间距与振痕深度是考察铸坯表面振痕情况的两个重要指标,尤其是振痕深度,其值的大小直接反应出铸坯表面质量的优劣。
随着结晶器的周期性上下振动,在铸坯表面会形成具有一定分布规律的振痕,振痕之间的距离——振痕间距可由下式进行计算[3]。

式中,p为振痕间距,mm;vc为拉坯速度,m/min;f为振动频率,次/min。
振痕深度受多种因素的影响,钢种的化学成分、润滑方式、保护渣的粘度、结晶器的振动方式与振动参数等都会影响振痕的深度。大量研究指出,采用相同的润滑方式、保护渣的粘度浇注特定的钢种时,振痕深度与振动工艺参数相关,振痕深度随着负滑动时间的增大而增大,如图2所示[4]。
振痕深度与负滑动时间的关系由下式给出[3]

式中,d为振痕深度,mm;k为比例常数,(N/s)1/2;tn为负滑动时间,s;η为保护渣粘度,Pa·s。
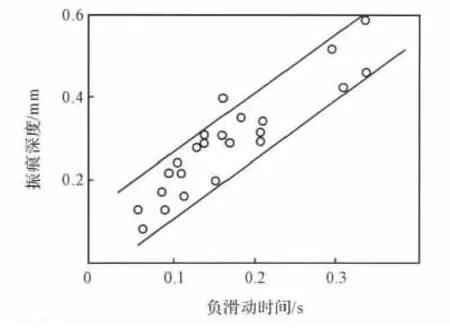
图2 振痕深度与负滑动时间之间的关系Fig.2 Relationship between the depth of oscillation marks and the negative strip time
3 保护渣消耗
充足的保护渣消耗量确保结晶器内壁与铸坯之间有足够厚度的渣膜,并是结晶器内壁与铸坯润滑良好的前提,关于渣膜是在结晶器振动周期的哪段时间里形成的,目前尚无统一意见,多数研究学者认为渣膜是在正滑动时间形成的,也有人认为熔渣在正、负滑动时间有流入。Jun-ichi OHTAKE等通过实验证明,熔渣在一个振动周期内均有流入,只是与负滑动时间相比,熔渣在正滑动时间里流入速度明显要快,流入量明显要大[5]。连铸结晶器最佳振动模式确定原理如图3所示。由图3可知,正滑动时间的增大有助于保护渣消耗量的增加,从而使得液渣膜厚度增大,铸坯与结晶器之间的液体摩擦力减小,润滑改善。
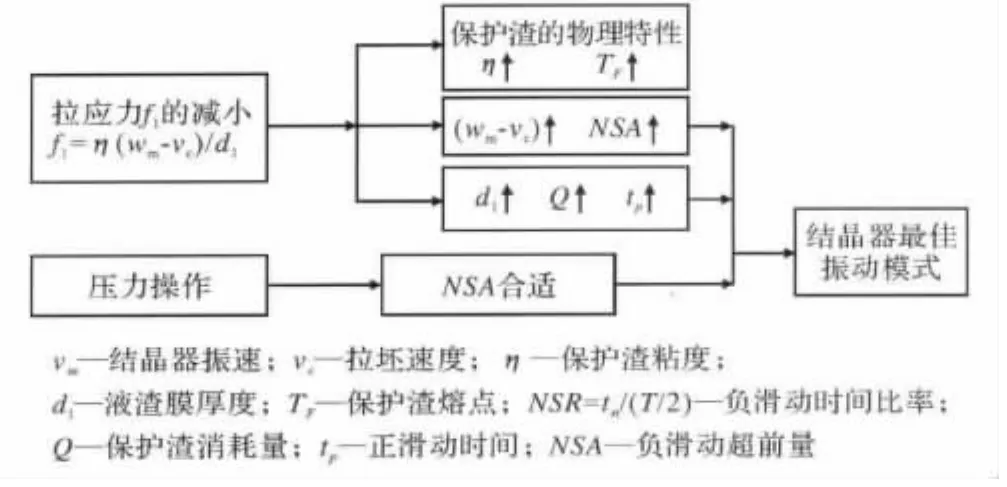
图3 连铸结晶器最佳振动模式确定原理Fig.3 Determination principle of the best oscillationmode of continuous casting
张洪波提出了一种保护渣消耗机制,其认为保护渣消耗量与正滑动时间成正比,与拉速、保护渣粘度成反比,并给出了保护渣消耗量的计算式[6],如
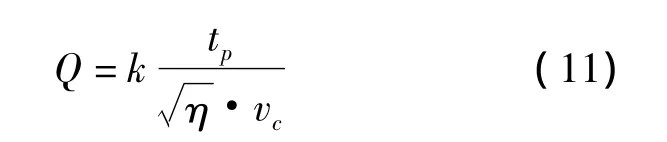
式中,Q为保护渣消耗量,kg/m2;k为比例常数;tp为正滑动时间,s;η为保护渣粘度,Pa·s;vc为拉坯速度,m/min。
4 振动参数的优化研究
负滑动时间的大小会影响振痕深度,为了减小振痕深度,应设法降低负滑动时间。连铸结晶器振动采用反向控制模型,其振幅、频率、波形偏斜率由6个振动参数决定,这为工艺参数的在线优化调整提供了方便。在实际浇注中,只需合理调整这6个参数即可减小铸坯表面振痕深度,提高铸坯表面质量。因此,有必要深入研究振动参数对振痕深度的影响,以便为振动参数的优化调整提供理论依据。
结晶器振动工艺效果通常由振动工艺参数来表示,主要包括负滑动时间tn、正滑动时间tp、负滑动率NS、负滑动时间比率NSR、负滑动超前量NSA和正滑动速度差△v等,制定工艺时通常以tn和tp为主。研究表明,振痕深度随着负滑动时间的减小而减小[7-8],保护渣消耗量随着正滑动时间的增大而增大[9-10],通过选择合适的保护渣与负滑动时间可减小铸坯表面振痕深度。在所使用保护渣相同的情况下,通过合理优化调整振动参数C来降低负滑动时间、增大正滑动时间,可达到减小铸坯表面振痕深度、改善润滑、优化铸坯表面质量的目的。
图4~图13分别是负滑动时间tn和正滑动时间tp与振动参数C及拉速vc的函数关系图。
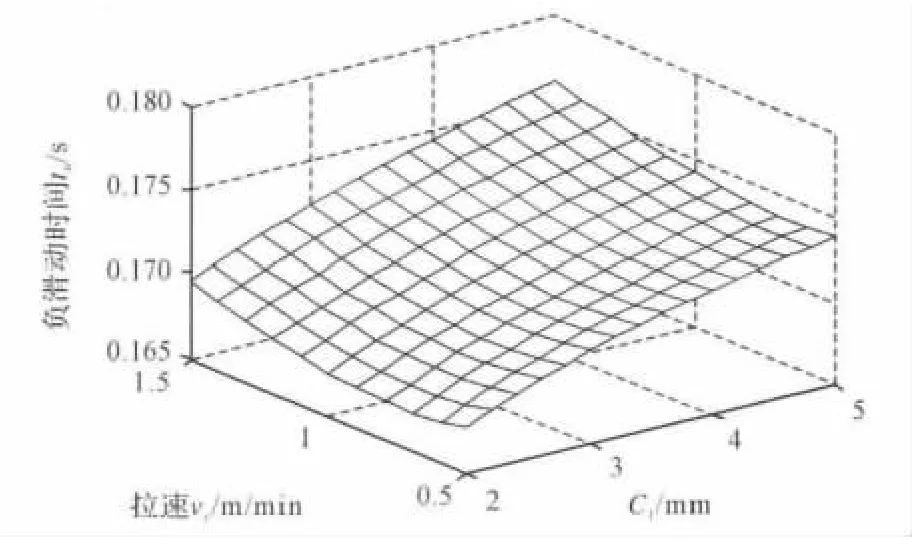
图4 负滑动时间tn与C1、拉速vc关系图Fig.4 Relationship among the negative strip time tn,C1and vc
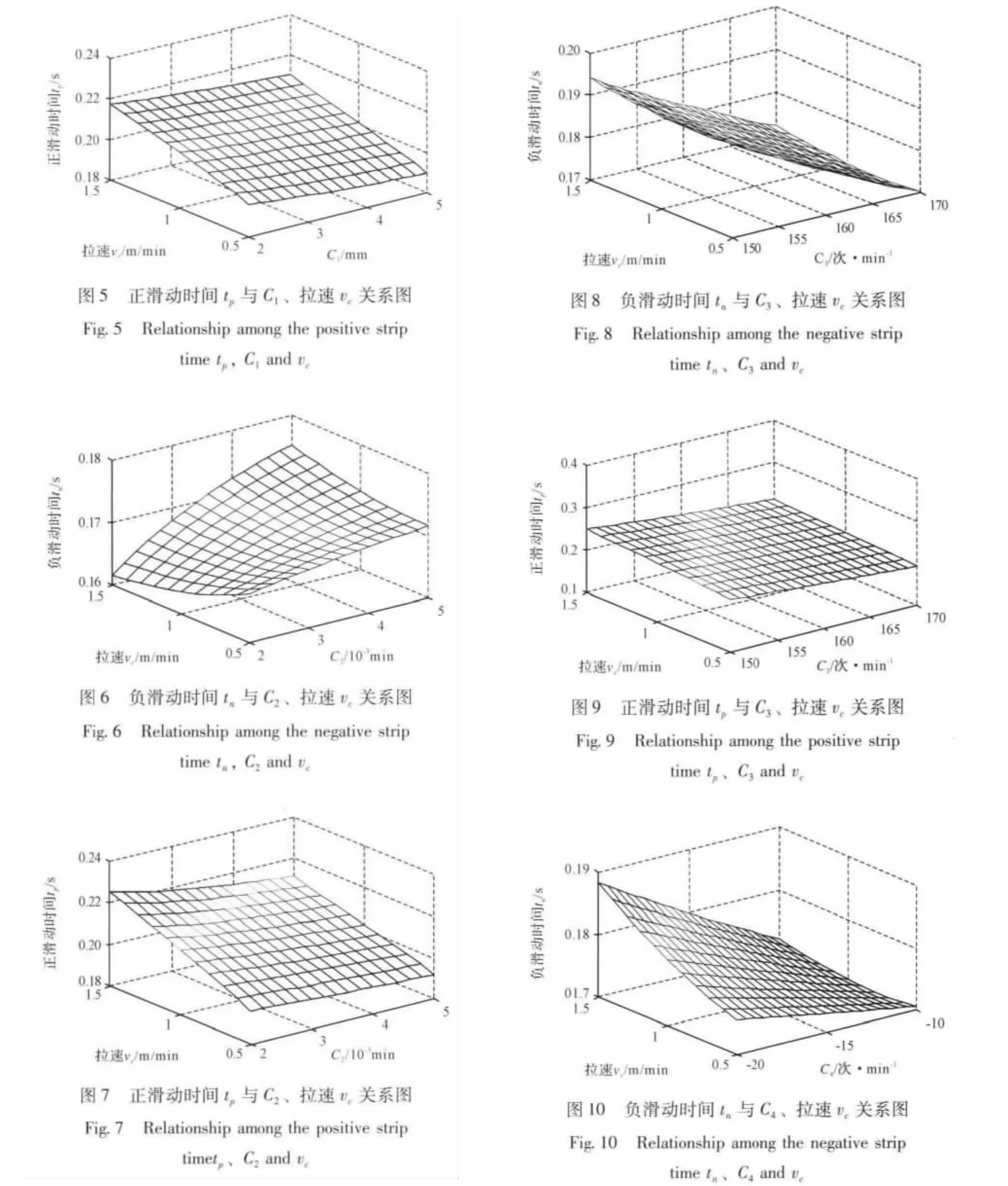
图4~图13是通过稳定其中5个振动参数来研究正、负滑动时间与另外一个振动参数及拉速的关系。若改用其他组振动参数,各振动参数对正、负滑动时间的影响规律相同。
图4、图5分别为C2=4(10-3min)、C3=170次/min、C4=10次/m、C5=0、C6=0.5时,负滑动时间tn和正滑动时间tp与C1及拉速vc的函数关系图。由图4、图5易知,在拉速vc的选择区间内,减小C1可使负滑动时间tn减小,有利于减轻振痕、改善铸坯表面质量;同时可使正滑动时间tp增大,增加保护渣消耗量,改善润滑。
图6、图7分别为C1=3 mm、C3=170次/min、C4=-10次/m、C5=0、C6=0.5时,负滑动时间tn和正滑动时间tp与C2及拉速vc的函数关系图。由图6、图7易知,在拉速vc的选择区间内,减小C2可使负滑动时间tn减小,有利于减轻振痕、改善铸坯表面质量;同时可使正滑动时间tp增大,增加保护渣消耗量,改善润滑。
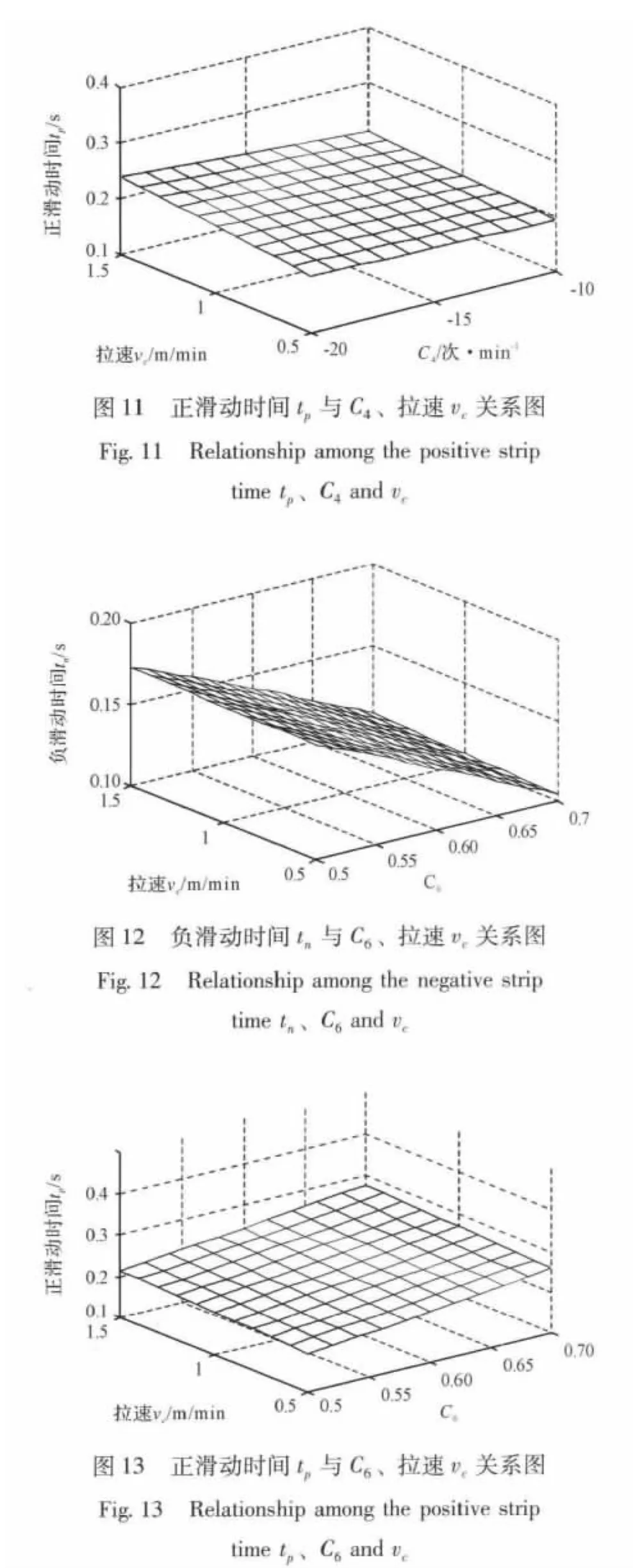
图8、图9分别为C1=3 mm、C2=4(10-3min)、C4=-10次/m、C5=0、C6=0.5时,负滑动时间tn和正滑动时间tp与C3及拉速vc的函数关系图。由图8、图9易知,在拉速vc的选择区间内,减小C3可使正滑动时间tp增大,增加保护渣消耗量,改善润滑;但同时也带来了负滑动时间tn增大的负面影响,使得铸坯振痕变深;减小C3可使振动频率减小,使得结晶器振动平稳,提高其使用寿命。减小C3致使负滑动时间tn增大,可通过调整其它参数进行弥补。
图10、图11分别为C1=3 mm、C2=4(10-3min)、C3=170次/min、C5=0、C6=0.5时,负滑动时间tn和正滑动时间tp与C4及拉速vc的函数关系图。由图10、图11易知,在拉速vc的选择区间内,减小C4可使正滑动时间tp增大,增加保护渣消耗量,改善润滑;但同时也带来了负滑动时间tn增大的负面影响,使得铸坯振痕变深;减小C4可使振动频率减小,使得结晶器振动平稳,提高其使用寿命。减小C4致使负滑动时间tn增大,可通过调整其它参数进行弥补。
通常情况下,C5一般均设置为0,本文不考虑其对振动工艺参数的影响。
图12、图13分别为C1=3 mm、C2=4(10-3min)、C3=170次/min、C4=-10次/m、C5=0时,负滑动时间tn和正滑动时间tp与C6及拉速vc的函数关系图。由图12、图13易知,在拉速vc的选择区间内,增大C6可使负滑动时间tn减小,且减小幅度较大,有利于减轻振痕、改善铸坯表面质量;同时可使正滑动时间tp增大,增加保护渣消耗量,改善润滑。
总之,须结合生产实际情况综合调整以上6个振动参数,优化出适合某一特定钢种的一组振动参数,使其振痕较浅、铸坯表面质量较好、符合实际生产要求。
5 高碳钢振动参数的优化
某钢厂生产高碳钢所使用的振动参数见表1。针对高碳钢保护渣消耗较低的现象,在结晶器保护渣使用型号不变的条件下,按照上述分析规律对振动参数进行了优化调整,调整后的振动参数见表2。
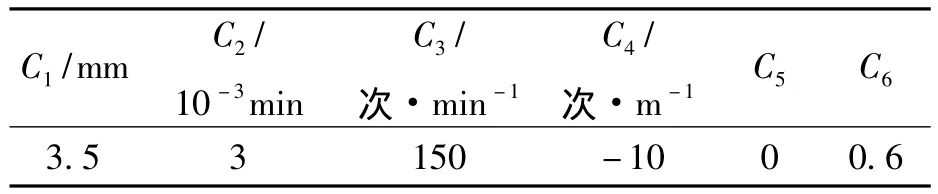
表1 原生产高碳钢用振动参数Tab.1 Oscillation parameters of high carbon steel
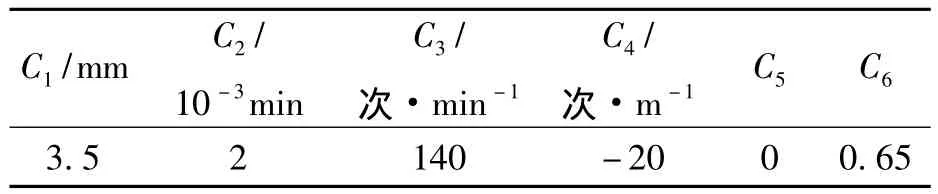
表2 优化调整后的振动参数Tab.2 Optimized oscillation parameters
根据式(7)、(8)计算可得出振动参数优化前后对应的正、负滑动时间对比见表3、表4。
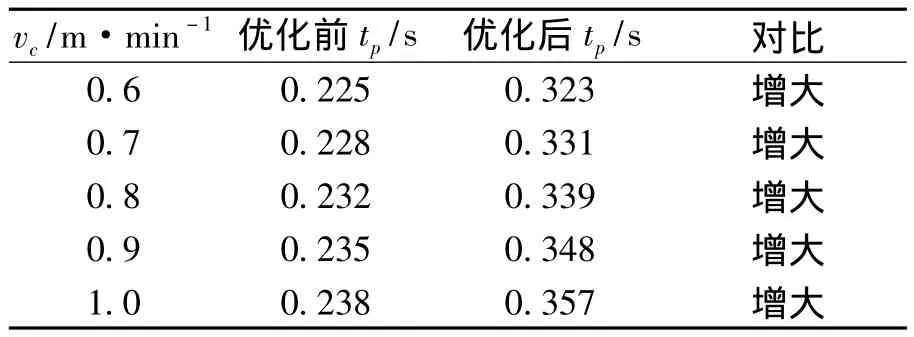
表3 振动参数优化前、后对应的正滑动时间tp对比Tab.3 Comparison of tpbefore optimization and after optimization
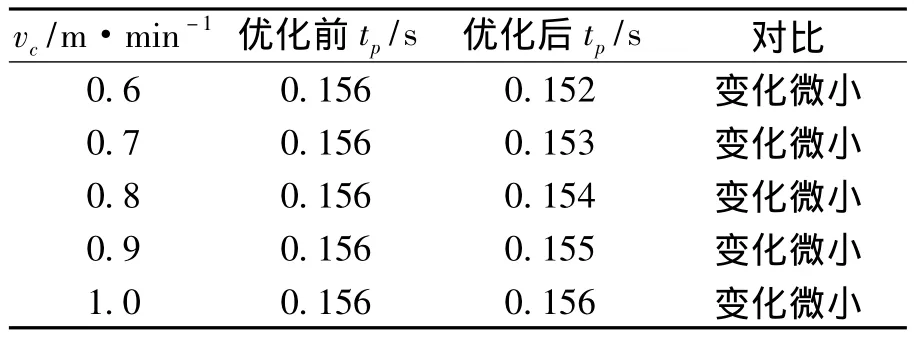
表4 振动参数优化前、后对应的负滑动时间tn对比Tab.4 Comparison of tnbefore optimization and after optimization
由表3、表4可知,在拉速增大时,负滑动时间近似为常数,有利于得到振痕深度均匀铸坯表面;在拉速增大时,正滑动时间增大,可有效弥补由于拉速增大引起的保护渣量降低;振动参数优化前后负滑动时间变化微小,而正滑动时间增大,因此振动参数优化后会使得保护渣消耗增大,而振痕深度变化极小。
基于优化后的振动参数,根据公式(11),计算保护渣消耗量,其结果如见表5。

表5 振动参数优化前、后保护渣耗量Q的对比Tab.5 Comparison of Q before optimization and after optimization
由表5可知,振动参数经优化调整,在拉速0.6~1.0 m/min范围内保护渣消耗提高25%左右。
振动参数优化后经现场使用反馈,保护渣消耗量偏低的现象得到了明显改善,证明振动参数的优化起到了一定的作用。但据反映,改善效果没有计算的(提高25%左右)那么好,这可能与所使用的保护渣消耗量计算公式不准确等其他因素有关,尚需进一步研究。
6 结论
(1)结晶器振动反向控制模型由于在拉速增大时振幅随着拉速的增大而增大,而频率呈下降趋势,使得负滑动时间近似为恒值,正滑动时间增大,有利于改善铸坯表面振痕深度,增加保护渣消耗量。
(2)振痕深度、保护渣消耗量与负滑动时间、正滑动时间有关,为连铸工艺的优化提供了便利。
(3)研究振痕深度、保护渣消耗量与反向控制模型C参数的关系,指出了振动参数优化的方向。
(4)针对某钢厂高碳钢保护渣消耗偏低的现象进行了振动参数的优化,经优化保护渣消耗得到了明显的改善。为了进一步改善保护渣的消耗量,选择低碱度、低粘度的保护渣可确保充分的渣耗量和润滑,此外根据实际生产情况适当降低拉坯速度也同样有利于保护渣的消耗。
[1]周小华.DYNAFLEX液压振动技术的应用[J].浙江冶金,2006,(2):14-16.
[2]孟祥宁,朱苗勇.高拉速连铸结晶器非正弦振动波形[J].过程工程学报,2006,(6):91-94.
[3]张林涛,邓安元,王恩刚,等.连铸坯表面振痕的形成及影响因素[J].炼钢,2006,22(4):35-39.
[4]张志强,张炯明.连铸坯表面振痕形成机理的研究[J].钢铁研究,2008,36(1):19-22.
[5]蔡娥,谢兵,王雨,等.连铸结晶器中保护渣渣膜润滑行为研究现状[C].攀枝花:中国金属学会,2003:242-247.
[6]张洪波,王海之.连铸结晶器振动参数与保护渣物化性能的关系[J].钢铁,1995,(11):17-20.
[7]Schwerdtfeger K,Sha H.Depth of oscillation marks forming in continuous casting of steel[J].Metallurgical and Materials Transactions B,2000,31B:813-826.
[8]Bo K,Cheng G G,Wu J,et al.Mechanism of oscillation mark formation in continuous casting of steel[J].Journal of University of Science and Technology Beijing,2000,7(3):189-192.
[9]Shin H J,Kim S H,Thomas B,et al.Measurement and prediction of lubrication,powder consumption,and oscillation mark profiles in ultra-low carbon steel slabs[J].ISIJ International,2006,46(11):1635-1644.
[10]Kawamoto M,Murakami T,Hanao M,et al.Mould powder consumption of continuous casting operations[J].Ironmaking and Steelmaking,2002,29(3):199-202.

