多元贝叶斯回归模型框架下绘制成本-效果可接受曲线Δ

彭娟，骆福添（中山大学公共卫生学院，广州510080）

成本-效果估计不可避免地含有不确定性，包括来自成本的或效果的。与成本-效果的点估计和区间估计相比，成本-效果可接受曲线（CEAC）是一种直观地描绘成本-效果估计中不确定性的绘图方法。然而，传统方法在该曲线的解释上比较牵强，使得贝叶斯方法在成本-效果分析中得到广泛应用。尽管该方法在国外的研究和应用已相对较多，但在国内的研究却很少。在中国知网、万方数据库等搜索，只有几篇介绍该方法的文章。张玉哲等[1]介绍贝叶斯法可利用先验信息进行推测，可在理论上准确地提供增量成本-效果比、CEAC、净货币收益的概率阐述；吴晶等[2]给出了CEAC的计算方法，但如何实现CEAC，特别是在贝叶斯框架下如何实现CEAC并未讨论。因此，CEAC如何绘制、为什么要采用贝叶斯方法来绘制等问题亟待解决。本文就贝叶斯方法的优势、在贝叶斯回归框架下如何绘制CEAC作了深入探讨，同时比较了在不同先验信息下CEAC的区别。文章分析基于模拟实验，模拟实验利用R与Openbugs软件实现。

1 贝叶斯方法的优势

从贝叶斯估计来讲，在获得样本之前，有一部分经验的、历史的信息称为先验信息。贝叶斯参数的后验分布其实就是似然函数和先验分布的乘积。而贝叶斯估计是通过后验分布得到的。因此，在无先验信息或弱先验信息（参数几乎等概率的在取值范围内取值）下，贝叶斯估计应该与极大似然估计一致。当先验分布有效利用了先验信息时，贝叶斯估计应该更加准确，抽样随机性影响更小。从贝叶斯区间估计来讲，贝叶斯方法假设参数是随机的，可计算出该参数落入任一子域内的概率；对给定概率，可找到一些区域，贝叶斯区间选择使得该区域上的后验密度值不少于相同概率下其他区域上的值，也就是最高后验密度的区域即相同概率下最短的区域。由此得到的区间可解释为该参数落入其中的概率为1－α，这与实际中的理解吻合。而传统方法通过构造统计量，解释为当抽样次数达到很大时，大约有100×（1－α）个区间覆盖真值。1－α为置信水平，在解释上比较牵强。因此，贝叶斯方法综合利用了先验信息和样本信息，对统计推断能给出一个直观的解释。而传统方法作出的推断总是基于频率的基础，对估计值的统计性质实际上是对大量重复实验作出的推断，不能对当前估计值的统计性质给出一个明确的答案，在应用中含有更多的不确定性。

2 探讨贝叶斯框架下CEAC的计算

当卫生决策者在决定是否补偿某种卫生技术时，比较新技术和已有技术的效果和成本-效果分析显得越来越重要。假设在一个临床试验中，要比较2种医疗技术T1、T2。数据

eij、cij分别代表接受第i种治疗的第j个患者的效果和成本。为了比较哪一个方案的成本-效果更好，首先得知道各个方案的期望成本和期望效果。令ΔE＝μ2－μ1、ΔC＝γ2－γ1，代表平均效果差异和平均成本差异。常用指标是增量成本-效果比ρ＝ΔC/ΔE，代表在原有基础上额外增加1个单位效果所需的额外成本。当比值ρ＞λ，就代表T2是更好的。λ表示社会为增加单位效果支付的最大数额，此时λ是某个固定的阀值。

另一方面，ρ＞λ等价的表示为增量净效益（INB）＞0。INB＝λΔE－ΔC，λ是为增加单位效果意愿支付的最大货币值，是可变的常数。同样，由于ΔE、ΔC估计的不确定性，INB的估计值也具有不确定性，并且INB估计的分布由ΔE、ΔC的联合分布来表示。当λ取值固定时，可得到INB＞0的概率。对一系列λ，可绘制INB＞0的概率的曲线图，即CEAC。原理如下：

考虑第i种治疗的抽样模型f（ei，ci│θj），i＝1、2，θj代表未知的不可观察的参数。数据的似然函数为：

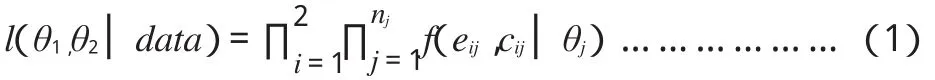
治疗方案间独立，对某个贝叶斯模型，π（θj），i＝1、2为θj的先验分布。假设参数间是独立的，（θ1，θ2）联合后验分布为：

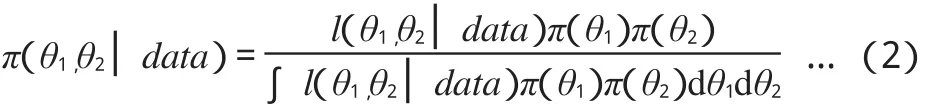
临床试验中，期望用个体的临床特点和接受的治疗方案的线性组合来解释患者的成本和效果，于是多重贝叶斯回归可写成如下形式：

假设（ei，vi）是误差项，是独立的且一致服从多元正态分布，为精度矩阵。指定参数服从多元正态先验分布，即假设，对协方差结构服从逆威沙特分布λ～IW（A，f）[3]。

变量xTi的系数bT、cT，分别代表新、旧治疗方案相比平均增加的效果和成本，其他协变量的系数也类似解释，于是增量成本-效果的联合分布体现为bT、cT的联合分布。在马尔可夫链蒙特卡洛模拟技术（MCMC）算法下，得到一系列来自参数联合后验分布的样本。绘制CEAC得计算不同λ下，INB＞0的概率。而INB的分布较难获得，可通过来自INB的分布的样本来估计概率。

由INB＝λΔE－ΔC，而ΔE、ΔC的样本可通过MCMC方法得到，因此可直接利用回归系数的模拟样本得到INB的样本。在大样本的基础上，可利用大数定律直接得到INB＞0的概率，从而绘制出CEAC。具体实现见程序部分。

3 模拟实验分析

在R软件中生成模拟数据，模型程序在Openbugs软件中实现，所用模拟数据来自模型：

用模型（4）生成模拟数据，在Openbugs中实现多元贝叶斯回归模型，模型的结果包括参数估计以及不同λ下INB＞0的概率。主体程序如下：

model{

for（i in 1：N）{

output[i，1：2]～dmnorm（mu[i，1：2]，v[1：2，1：2]）；#output＝[cost，effect]

mu[i，1]<-alpha[1]+alpha[2]*age[i]+alpha[3]*treat[i]；

mu[i，2]<-beta[1]+beta[2]*age[i]+beta[3]*treat[i]；

}

v[1：2，1：2]～dwish（A1[，]，f1）；#精度阵服从威沙特分布

alpha[1：3]～dmnorm（a[]，A[，]）；#系数服从多元正态分布

beta[1：3]～dmnorm（b[]，B[，]）；

for（k in 1：NK）{

Q[k]<-step（K[k]*alpha[3]-beta[3]）#Q[k]＝1如果式子＞0

}

var[1：2，1：2]<-inverse（v[1：2，1：2]）

deviation1<-sqrt（var[1，1]）

deviation2<-sqrt（var[2，2]）

correlation<-var[1，2]/（deviation1*deviation2）

}

模型的先验分布用真值a＝c（20，1，10），b＝c（100，2，30）作为均数。设定A，B的值作为可以表示对系数alpha、beta估计值的把握度。如在强先验信息下，令上述均数的变异度为0.01；在弱先验信息下，令上述均数的变异度为100。此时，a、b可取范围内的任意值，相当于没有特定先验信息。显然，在强先验信息的情况下，参数估计的变异程度和准确度应该更好。如表1所示，各个参数第1行是弱先验信息的估计，第2行是强先验信息的估计。实际情况与预期吻合。不管是强先验信息，还是弱先验信息，MC_error都很小，说明本次模拟结果很稳定。从参数后验分布的均值和标准差都可看出强先验信息下的估计准确度高、变异程度小；中位数和均数比较差异均＜0.01，说明参数后验分布对称，符合正态分布假设。

图1以强弱先验信息下绘制的CEAC为例来说明2种方法在参数解释上的差异。INB（Rc）＝RcΔE－ΔC，Rc表示增量效果意愿支付的货币值，INB代表增量净效益，prob代表INB＞0的概率。

图1中，曲线在点Rc＝0.93时，p＝0.50，贝叶斯派的解释为当增加单位效果患者愿意付超过0.93元时，选择治疗有较大的把握能够获得盈利，而不是亏本。这里的把握程度会随着Rc的取值慢慢增大，即概率值增大。但是按频率派的解释，当患者愿意支付超过0.93元时，重复100次这样的治疗，大约有超过一半的治疗会盈利，而不是亏本，至于该次治疗的增量-净效益会不会＞0，是未知的，无法作出推断。

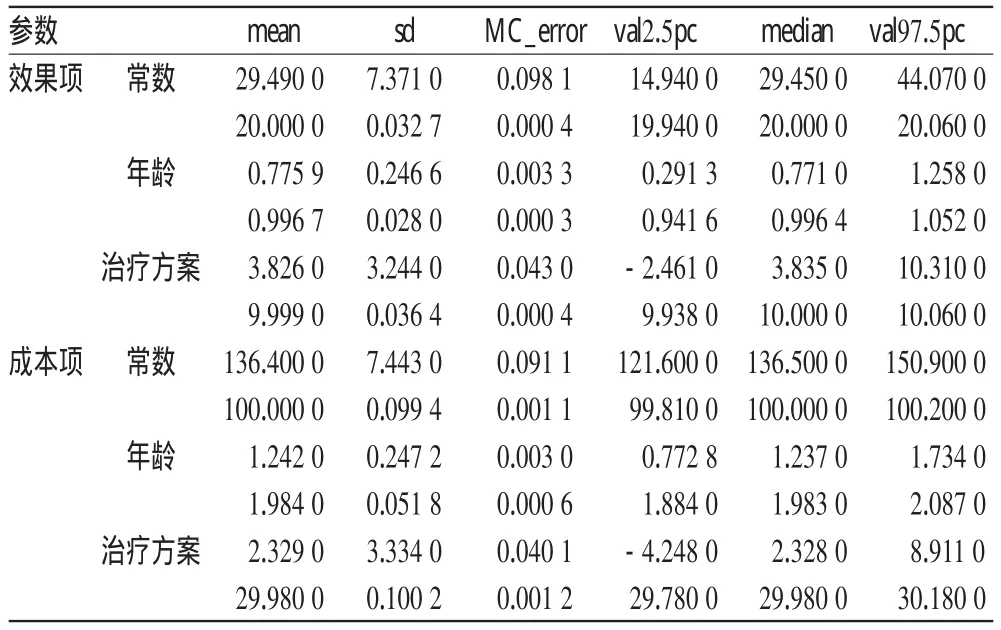
表1 强弱先验下参数估计比较Tab 1 Comparison of parameter estimation under strong and weak prior information

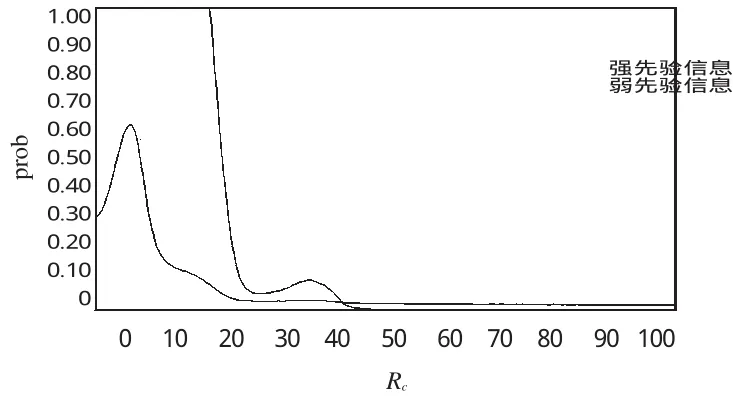
图1 成本-效果可接受曲线Fig 1 Cost-effectiveness acceptability curves

从图1中可看出，在Rc＝3.05时，强先验信息下INB＞0的概率为0.56，而弱先验信息下的概率达0.8。在强先验信息下，选择第2种方案的把握不是很大，有可能选择第1种方案；而在弱先验信息下，毫无疑问选择第2种方案。说明在意愿支付额较小时，决策的不确定性较大。弱先验信息下的结论并没能反映出此时决策的不确定性。而在Rc＞3.05时，强先验信息信息下，对本次数据结果的INB＞0的概率均大于弱先验信息下的概率。表明在有可靠先验信息的情况下，对同一数据的结果所得INB＞0的把握度（信念）是不一样的。进一步说明，在信息准确的情况下，先验信息可增强结果的可靠性。

4 结果与讨论

在意愿支付法下，本文引出了增量-净效益，进而自然提出CEAC。然而，对CEAC的解释有学者提出质疑，认为在贝叶斯框架下解释才合理。有必要指出的是，本文中增量-净效益有文现状也称净货币效益。Briggs AH等[4]定义INB（Rc）＝RcΔEΔC。Rc是用来度量单位效果差异的货币。Löthgren M等[5]同样用该式来定义INB。两种说法相同。

本文详细地分析了成本-效果回归框架下CEAC是如何绘制的问题，并通过实际数据分析给出了程序。同时，通过CEAC的比较，可得出当前支付额度下，某种治疗方案或技术成本效果更优的概率有多大。本文研究显示，对不同的先验信息、经验信息越准确，把握度越大，在意愿支付法下，对当前决策的把握会更大。

对CEAC的计算，有学者[6]提出INB基于平均值的计算偏优于对称分布，对偏态分布的效果较差，因此有学者提出另一种计算方法——预测联合密度方法。当然，本文对成本-效果分析中的一些问题讨论得还不够全面，如在贝叶斯回归框架下，CEAC的推理、MCMC方法的具体计算等。另外，有学者将研究扩展到对3种以上治疗技术的比较[7]。

[1]张玉哲，吴晶，孙利华.药物经济学评价中的贝叶斯法介绍[J].中国药物经济学，2009（2）：51.

[2]吴晶，刘国恩.成本-效果可接受曲线：不确定状态下的医疗决策方法[J].中国药物经济学，2006（3）：52.

[3]朱慧明，林静.贝叶斯计量经济模型[M].北京：科学出版社，2009：66-67.

[4]Briggs AH.A bayesian approach to stochastic cost-effectiveness analysis[J].Health Econ，1999，8（3）：257.

[5]Löthgren M，Zethraeus N.Definition，interpretation and calculation of cost-effectiveness acceptability curves[J].Health Econ，2000，9（7）：623.

[6]Hernández MA，Vázquez-Polo FJ，González-Torre FJ，et al.Complementing the net benefit approach：a new framework for bayesian cost-effectiveness analysis[J].Int J Technol Assess Health Care，2009，25（4）：537.

[7]宗欣，孙利华.成本-效果可支付曲线的理论与应用[J].中国药房，2012，23（10）：867.