基于单元模态应变能变化率的电力构架损伤识别
张 猛,赵桂峰,秦志伟,李 天
(郑州大学 土木工程学院,河南 郑州450001)
0 引言
电力构架是变电站中支撑导线和悬挂变电设备的主要结构构件,其承载能力的可靠性将直接影响设备的工作性能以及变电站和整个电力系统的正常运行.目前,国内多数变电站针对电力构架的损伤检测主要采用目测法、回弹法、射线法、超声波技术等局部检测方法[1-2].这种局部检测方法需要预先知道结构损伤的大体位置,并且要求检测仪器能够到达损伤区域,这对于简单构架是适用的,但对于大型复杂电力构架结构,则无法给出整体结构的损伤信息,而且检测效率低下.
笔者以现代大型变电站中常用的钢结构电力构架为例,采用在建筑结构损伤识别中常用的单元模态应变能变化率方法[3]对电力构架进行损伤识别,通过对不同损伤部位和不同损伤程度下的识别结果的分析,验证该法在电力构架损伤识别中的可行性和有效性.
1 损伤识别的基本理论
利用损伤发生前后结构动力参数特性的改变来诊断结构损伤的方法称为整体检测方法,其原理是建立与结构动力特性有关的损伤标示量,然后根据标示量的变化来识别损伤[4].
单元模态应变能变化率方法就是一种将单元模态应变能作为标示量的结构损伤识别方法.该方法的推导过程如下[5-7]:如果不考虑阻尼的影响,结构运动的微分方程为

式中:M为结构质量矩阵;K为结构刚度矩阵;x为结构的位移列阵.式(1)所对应的特征方程为

式中:φ为结构的振型;λ为特征值.由于结构损伤前后,单元的刚度发生变化,质量一般不变,因此,一个具有多自由度的结构损伤时,其特征方程可写为如下的形式:
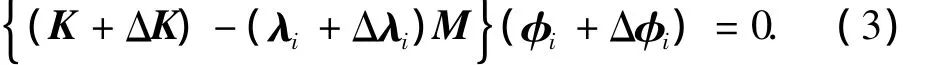
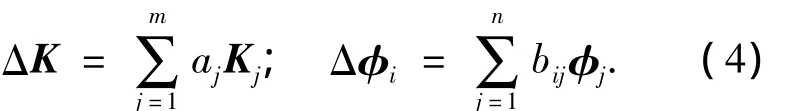
式中:m为结构的单元总数;n为需要考虑的模态数目;aj为单元损伤系数;bij为振型改变系数.

将式(4)代入式(5),并整理可得

当 γ =i时,由 φTγMφγ=1以及 ΔM=0 可知,biγ=0.
当采用单元模态应变能变化率作为结构损伤的识别指标时,可定义结构损伤前后的单元模态应变能分别为式(7)和式(8)


研究表明,结构损伤后的刚度可近似用损伤前的刚度代替,而且单元模态应变能的改变量对结构局部损伤比较敏感,故可将式(9)改写为:
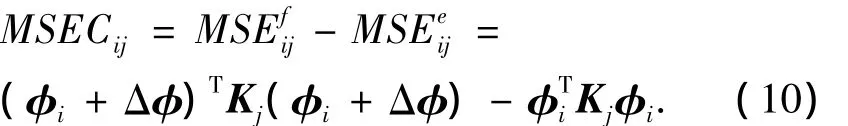
将式(10)展开,利用其正交性,并且略去高阶项,可得

将式(6)代入式(11),可得到结构中第j个单元第i阶模态应变能变化量为

若假设整个结构中的第p个单元发生损伤引起结构的单元模态应变能变化,则可以将式(4)代入式(12),得

假设当结构中n个单元发生损伤时,将式(4)代入式(12),并化简整理可得

式(14)表明,多位置损伤状况下的模态应变能变化率是由单位置损伤状况下的模态应变能变化率叠加得到的.
设多位置损伤时总的单元一阶模态应变能变化率向量为φ,单一位置损伤时各自单元的一阶模态应变能变化率数据库为φρ(a),ρ(a)为相应单元的损伤程度,其取值范围为[0,1];a为损伤单元,取值范围为[1,n].这样在多位置损伤时,总的单元一阶模态应变能变化率向量可以近似表示为单一损伤时相应损伤程度下单元一阶模态应变能的线性组合,所以多位置损伤诊断就转化成了一个数学问题,其目标函数如下:

当实际损伤状态下结构的单元一阶模态应变能变化率与相对应损伤单元处的单一损伤状态下的单元一阶模态应变能变化率的叠加向量之差的2范数最小时,即式(15)取最小时,实际的损伤状态便由此时取得最小值的单一位置损伤状态组合优化而成.该方法的优点便是不需建立多位置损伤工况下的数据库,只需建立单一位置损伤工况下的数据库,然后组合即可.
2 电力构架损伤识别分析
2.1 电力构架计算模型
某500 kV变电站电力构架的计算模型[8]如图1 所示.A1A2=5.8 m,A5A6=3.792 m,A8A9=1.784 m.A5A6距离地面高 9 m,A8A9距离地面高18m,横梁距地面高26m,跨度为28 m.A3到A1A2的距离为 5.6 m,A4到 A5A6的距离为 3.662 m,A7到A8A9的距离为1.723 m.设计时,侧向支撑柱A10A3与人字形柱顶之间采用销子连接,4个连接杆A4A5、A4A6、A7A8和 A7A9与人字形柱和支撑柱之间搭接,计算的这些连接点按铰接考虑,其余连接点均按刚接考虑.人字形柱、支撑柱以及所有连接杆采用直径420 mm、壁厚6 mm的圆钢管,横梁为格构式钢梁,钢材等级为Q235.
以构架支柱产生损伤为例进行识别分析,采用减小弹性模量的方法来模拟结构损伤.建模时将构架的每个支腿柱和侧向支撑分别划分为90个单元,两个支腿之间的横撑以及支腿柱与侧向支撑之间的连接杆划分为30个单元.由于划分后的单元比较多,为了减少工作量,笔者仅研究带侧向支撑的构架柱的损伤工况,其划分后的单元排列如下:A1A10杆件依次为1~90号单元,A2A10杆件依次为91~180号单元,A3A10杆件依次为2 541~2 630号单元,各损伤工况如表1所示.

图1 电力构架计算模型Fig.1 Model of gantry structure
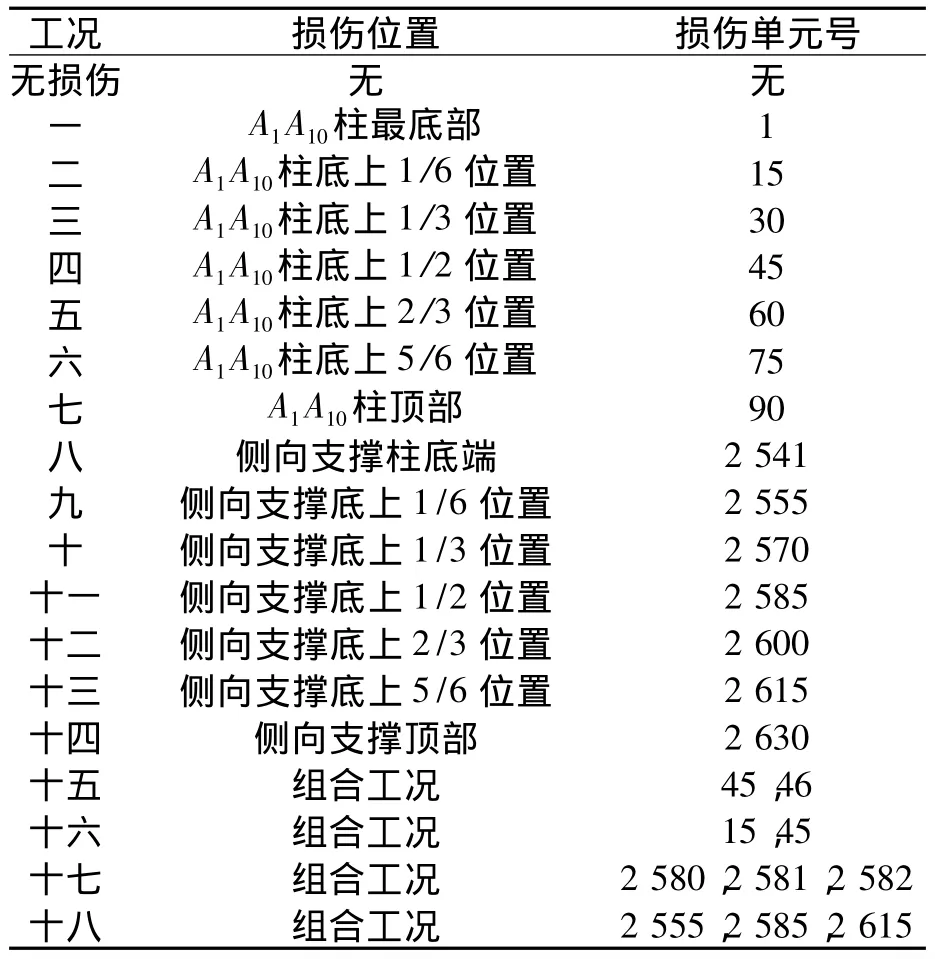
表1 电力构架的损伤工况Tab.1 Damage conditions of gantry structure
2.2 单一损伤工况的损伤识别
(1)损伤位置对电力构架单元模态应变能变化率的影响.图2为单一损伤工况转角度的单元一阶模态应变能变化率曲线.从图2可见,当损伤程度为10%时,单元一阶模态应变能变化率曲线图中的损伤程度均在10% ~12%间,其他未损伤部位的变化率均不大于0.其中工况一的损伤程度识别结果为10.22%,而且在损伤位置附近的单元的一阶模态应变能变化率接近1%,负向的波动比较大,这是由于1号单元位于结构的最底端,与固结支座相连,产生应力集中,引起损伤位置附近的单元应变能曲线波动.同样,工况八2 541号单元的识别结果亦表现出此规律.
(2)损伤程度对电力构架单元模态应变能变化率的影响.图3为电力构架中四处不同位置不同损伤程度时的单元一阶模态应变能变化率曲线图.从图3可见,当损伤程度较小时(5%、10%、20%),损伤位置处的应变能变化率与损伤程度之间的误差不大,随着损伤程度的加大,损伤位置处单元的应变能变化率和损伤程度之间的误差逐渐增大,两者呈现出非线性关系.
由此可知,根据单元一阶模态应变能变化率可对结构的单一位置损伤进行精确定位;随着损伤程度加大,单元的一阶模态应变能变化率曲线呈现非线性变化.这是因为式(9)向式(11)转化中采用了损伤前的刚度近似代替了损伤后的刚度以及略去了高阶项的缘故.因此要想精确识别单元的受损程度,需要知道受损单元的一阶模态应变能变化率和受损程度之间的非线性关系.
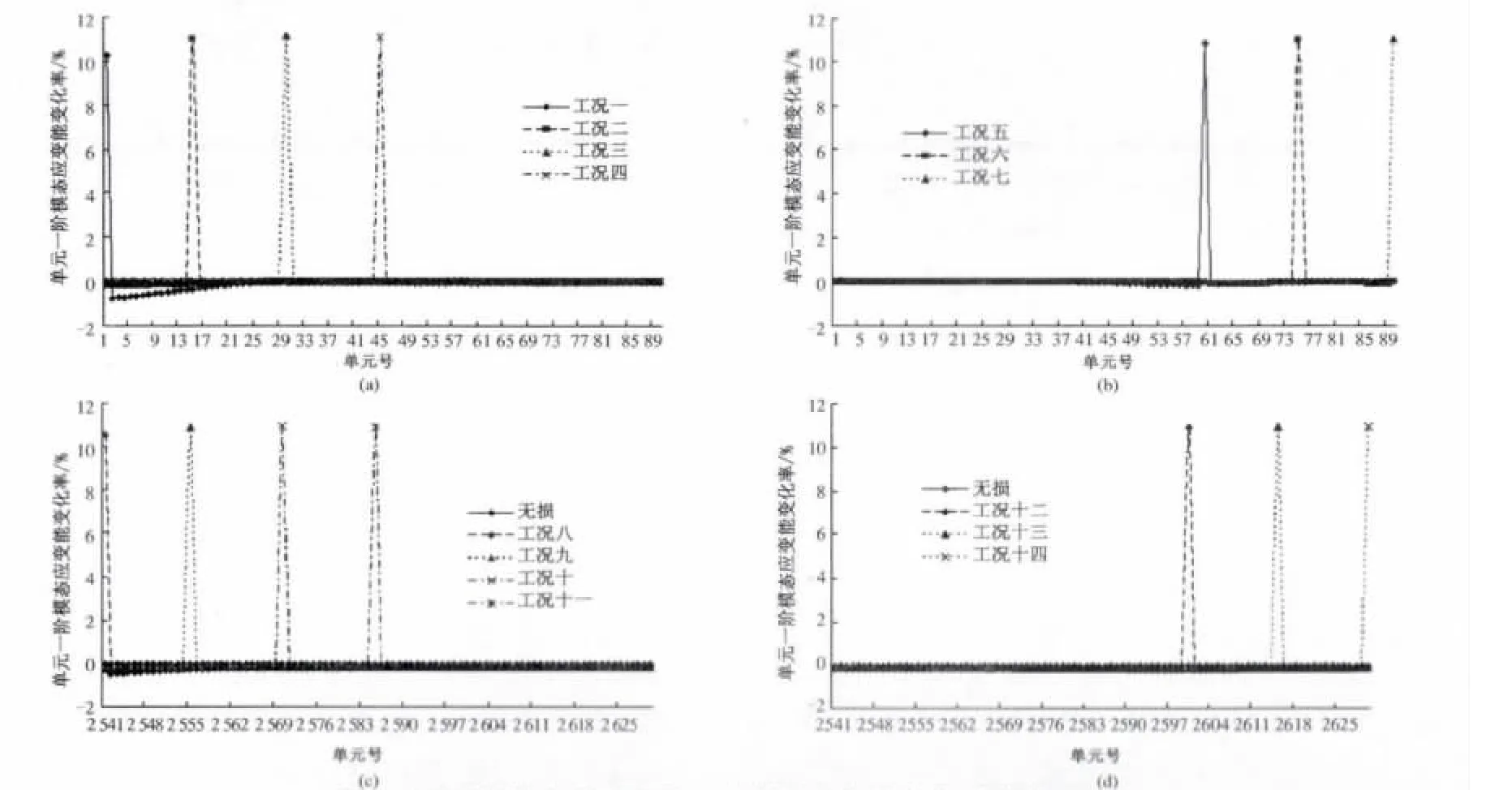
图2 不同损伤位置时单元一阶模态应变能变化率曲线图Fig.2 Change rate of the first-order modal strain energy with different damage position
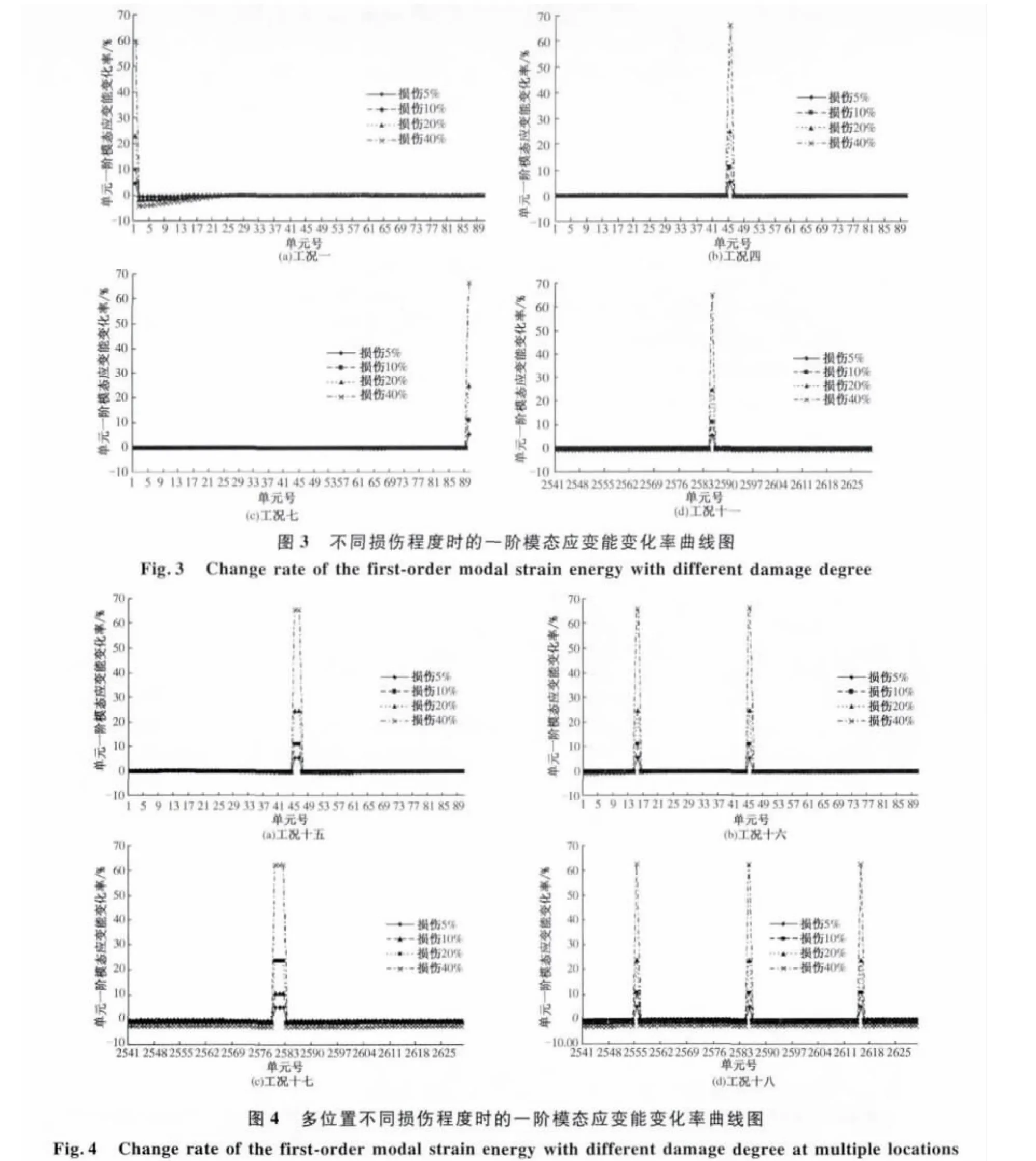
2.3 多位置损伤工况的损伤识别
2.3.1 不同损伤程度的多位置损伤识别
图4为电力构架中存在多位置损伤时,其单元一阶模态应变能变化率曲线图.另外,每个损伤位置处的单元一阶模态应变能变化率发生突变,没有发生损伤处的单元一阶模态应变能变化率很小,这说明单元一阶模态应变能变化率能够对多位置损伤工况下各个损伤位置进行精确定位.另外,不同损伤程度下总的单元一阶模态应变能变化率基本上为图3中各对应单元相应损伤程度下一阶模态应变能变化率的叠加.
2.3.2 多位置损伤诊断分析
在对电力构架进行损伤检测时,需要尽可能地预判损伤位置和损伤程度.为此,首先对整个电力构架进行分析,确定损伤后的单元一阶模态应变能变化率曲线图,根据曲线上的突变位置确定出损伤的位置.经过分析,发现构架侧向支撑杆件处模态应变能变化率曲线出现了突变,为节省篇幅,这里只给出损伤杆件的单元一阶模态应变能变化率曲线图,如图5所示.
由图5可见,损伤位置为2 570单元和2 600单元.由于多位置的单元一阶模态应变能变化率可由单一损伤位置处相应损伤程度的单元一阶模态应变能变化率叠加而成,故可建立单一损伤工况下的单元一阶模态应变能变化率数据库曲线,如图6所示.

由图5可知,2 570,2 600单元的一阶模态应变能变化率为76.80%,115.01%.由图6可知,当2 570,2 600单元损伤程度分别为45%、55%时,其一阶模态应变能变化率分别为79.86%、117.34%,与实际损伤的数值76.80%和115.01%最接近,可以使式(15)取最小值.由此,可以判定2 570,2600单元存在45%、55%的损伤,可见,该电力构架的损伤可以由单元一阶模态应变能变化率这个指标来识别,而且精度比较高.
3 结论
以现代大型变电站中常用的钢结构电力构架为研究对象,采用单元模态应变能变化率方法,对具有不同损伤部位和不同损伤程度的电力构架进行了损伤识别分析.研究表明:单元模态应变能变化率是受损钢结构电力构架的一个比较敏感的指标,采用该指标能够很好地对存在单一位置损伤或多位置损伤状态的电力构架进行损伤识别和定位.
[1] 李天,张猛,张哲,等.数值积分法计算受损伤圆钢管轴压杆件极限承载力[J].郑州大学学报:工学版,2004,25(1):11-15.
[2] 孙洪波,曹志民,刘鹏伟.河南省电网变电站建(构)筑物可靠性分析与评价研究[J].河南电力,2005(3):5-8.
[3] 郭惠勇,李正良,彭川.结构损伤动力识别技术的研究与进展[J].重庆建筑大学学报.2008,30(1):140-145.
[4] 朱宏平,余璟,张俊兵.结构损伤动力检测与健康监测研究现状与展望[J].工程力学,2011,28(2):1-17.
[5] 李永梅,胡琨,姚玄一,等.单元模态应变能变化率对框架结构的损伤诊断[J].工业建筑,2013,43(1):125-130.
[6] 郑飞,许金余,颜祥程.利用单元模态应变能法的地下框架结构损伤诊断[J].振动、测试与诊断.2010,30(6):642-645.
[7] DOEBLING SW,HEMEZ F M,PETERSON L D,et al.Improved damage location accuracy using strain energy-based onmode selection criteria[J].AIAA Journal,1997,35(4):693 ~699.
[8] 中南电力设计院.变电构架设计手册[M].武汉:湖北科学技术出版社,2006.

