一种基于复杂性测度的干扰样式识别方法*

张兴哲

(麻波亚理工学院 电子与通信系，菲律宾马尼拉)

一种基于复杂性测度的干扰样式识别方法*

张兴哲

(麻波亚理工学院 电子与通信系，菲律宾马尼拉)

提出了一种基于复杂性测度的干扰样式识别方法.该方法首先分析接收信号的分形维数和LZ复杂度.通过使用一定数量样本，获得每种干扰样式分形维数和LZ复杂度分布的均值中心和方差.然后采用指数距离计算待识别样本与每种干扰的均值中心和方差的距离，按最小距离原则来对干扰样式进行识别.最后给出了仿真结果及结论.

LZ复杂度；均值中心；方差；干扰样式

引言

近十年来，各种无线通信系统的应用日益广泛.然而随之而来的是，无线通信系统面临的电磁环境日益复杂，各种自然干扰和人为干扰严重影响着无线通信的有效性和可靠性[1].如能对干扰样式进行识别，并针对不同的干扰样式采取相应的抗干扰策略，将有效提高通信过程的可靠性[2].目前，干扰样式识别方面的文献还不多见.如文献[3]介绍了一种基于高阶累积量与神经网络的干扰识别算法，使用二阶、四阶累积量及其三次方作为特征参数，并结合神经网络进行识别；文献[4]提出了一种复合式干扰识别方法，采用盲源分离与支持向量机对复合式干扰进行分类和识别.马合意等人首先对干扰信号的频谱进行小波包分解，提取特征参数，然后利用支持向量机对干扰进行分类；文献[5]使用13种特征参数对直扩系统中的多种干扰样式及其调制方式进行识别；文献[6]使用FICA算法实现了四种干扰样式和两种通信信号的分离与识别.上述研究对复杂电磁环境下的干扰识别进行了初步探索，但存在计算复杂度较高、干扰样式识别种类不多等问题；或仅针对特定通信系统、特定干扰样式的检测与抑制.因此，这些算法的实际应用会有一定的局限性.

因此，本文提出了一种基于复杂性测度的干扰样式识别方法，能够对无线通信中常见的单音干扰、多音干扰、窄带干扰、脉冲干扰、宽带噪声干扰、跳频干扰、扫频干扰七种干扰样式及QPSK通信信号进行识别.该方法首先分析接收信号的分形维数和LZ复杂度.使用一定数量样本进行训练后，获得每种干扰样式分形维数和LZ复杂度分布的均值中心和方差.然后采用指数距离计算待识别样本与每种干扰的均值中心和方差的距离，按最小距离原则来对干扰样式进行识别.文章最后给出了仿真结果及结论.

1 系统模型

本文采用中频通信系统模型，系统模型框图如图1所示.二进制随机信源产生的二进制序列经QPSK基带调制后，再进行中频调制，送入信道.在信道中，中频通信信号中加入高斯白噪声(AWGN)作为环境噪声，并加入人为干扰.离散化的接收信号r(n)可表示为：

r(n)=s(n)+v(n)+J(n)

(1)

式中s(n)表示通信信号，v(n)表示加性高斯白噪声，J(n)表示人为干扰.在接收端，首先对接收信号进行预处理，然后进行干扰样式识别.

图1 系统模型框图

目前无线通信系统面临的常见干扰样式主要有单音干扰、多音干扰、宽带噪声干扰、部分频带干扰、脉冲干扰、扫频干扰和无干扰等，本文将这些干扰样式作为研究对象.

2 干扰样式识别算法

对照一般的模式识别定义[7]，可以给出干扰样式识别的定义，即根据干扰样式的特征或属性，利用以计算机为中心的机器系统，运用一定的分析算法自动认定干扰的样式.与一般的模式识别问题类似，它也包括三个基本问题，即干扰样式的特征选择与提取、训练学习、分类识别.

2.1基于复杂性测度的干扰样式特征参数选择

如上所述，干扰样式识别首先要解决的问题就是提取能够反映干扰样式的特征参数.复杂度全称复杂性测度，它是指物体复杂性程度的客观度量.在信号处理领域，复杂性测度能够有效地刻画信号波形特征.因此，本文采用复杂性测度来作为干扰样式的特征参数.目前，复杂度的定量描述，包括LZ复杂度、分形维数、信息熵、Lyapunov指数等.在信号处理领域中最常用的方法有两种，即LZ复杂度和分形维数.

LZ复杂度是A. Lempel和J. Ziv于1976年提出的.有限长序列的LZ复杂度是指随序列长度增加产生新模式的速度，它通过复制和添加两种简单操作来描述一个序列的特性[8].分形维数，是用来衡量一个几何集或自然物体不规则和破碎程度的数，它可以定量刻画分形特征，表征了分形体的复杂程度，分形的维数越大，其客体就越复杂.计算分形维数的方法有多种，如盒维数、相似维数、豪斯多夫维数和信息维数等.其中盒维数(Box dimension)由于计算相对简单，得到了广泛的应用.因此，本文采用LZ复杂度和盒维数来作为干扰识别的特征参数.

对于LZ复杂度，首先对信号采用“颗粒化”处理来提取信号的整体特征而忽略信号的细节.考虑一个接收信号的序列r(n)，其长度为N+1，均值M.将r(n)中的每一个样点与M比较.如果样点的值大于M，则将r(n)为1，反之r(n)为0.然后将得到的由0，1组成的新序列从左侧第一个抽样依次检查是否有新的子序列出现.如果有，则LZ复杂度值加1.这种二值颗粒化操作简单易行，但丢失了原始序列的许多有用信息.因此，我们提出了一种改进的颗粒化操作及LZ复杂度计算方法.其具体步骤如下[7].

1)计算相邻两时刻信号差的绝对值，得到序列{m(n)}.

m(n)=|r(n)-r(n+1)|,n=1,2,…,N

(2)

新序列{m(n)}可以降低噪声的影响，提高LZ复杂度对同类信号的聚集程度和不同类信号的分离程度.

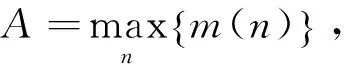
(3)

将得到的序列{mq(n)}进行二进制编码，最后得到二进制序列{h(n)，n=1,2,...,N·L}.

3)定义{h(n)}的子序列S和Q，SQ表示S和Q的合并序列.SQ〈D〉表示将SQ中最后一个接收信号抽样对应的L个二进制序列删除后剩余的序列.设初始复杂度C(0)=1，S=h(1)，Q=h(2)，SQ=h(1)h(2)，SQ〈D〉=h(1).

4)若S=h(1),h(2),...,h(i)，Q=h(i+1)，则SQ〈D〉=h(1),h(2),...,h(i).判断Q是否是SQ〈D〉的子集.

5)若Q属于SQ〈D〉，复杂度C(n)不变，S不变，Q=h(i+1)h(i+2)，继续第4)步.

6)若Q不属于SQ〈D〉，c(h)=c(h)+1，令S=SQ=h(1),...,h(i+j)，Q=h(i+j+1)，继续第4)步.

上述过程直到Q取到序列{h(n)}的最后一个二进制符号.为使复杂度值与序列长度无关，c(h)需要进行归一化处理.若序列{h(n)}的长度是N·L，则归一化的复杂度可写为：

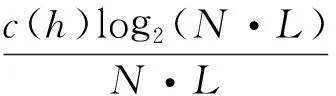
(4)

LZ复杂度反映的是一个时间序列中，模式数量随序列长度增加的速率.

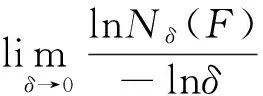
(5)

式中：Nδ(F)——以δ为边长的正方形网格与F相交的网格数.

按照这种思想，为计算长度为N时间序列r(n)的盒维数，用边长为δ的方格覆盖r(n)，如图2所示.

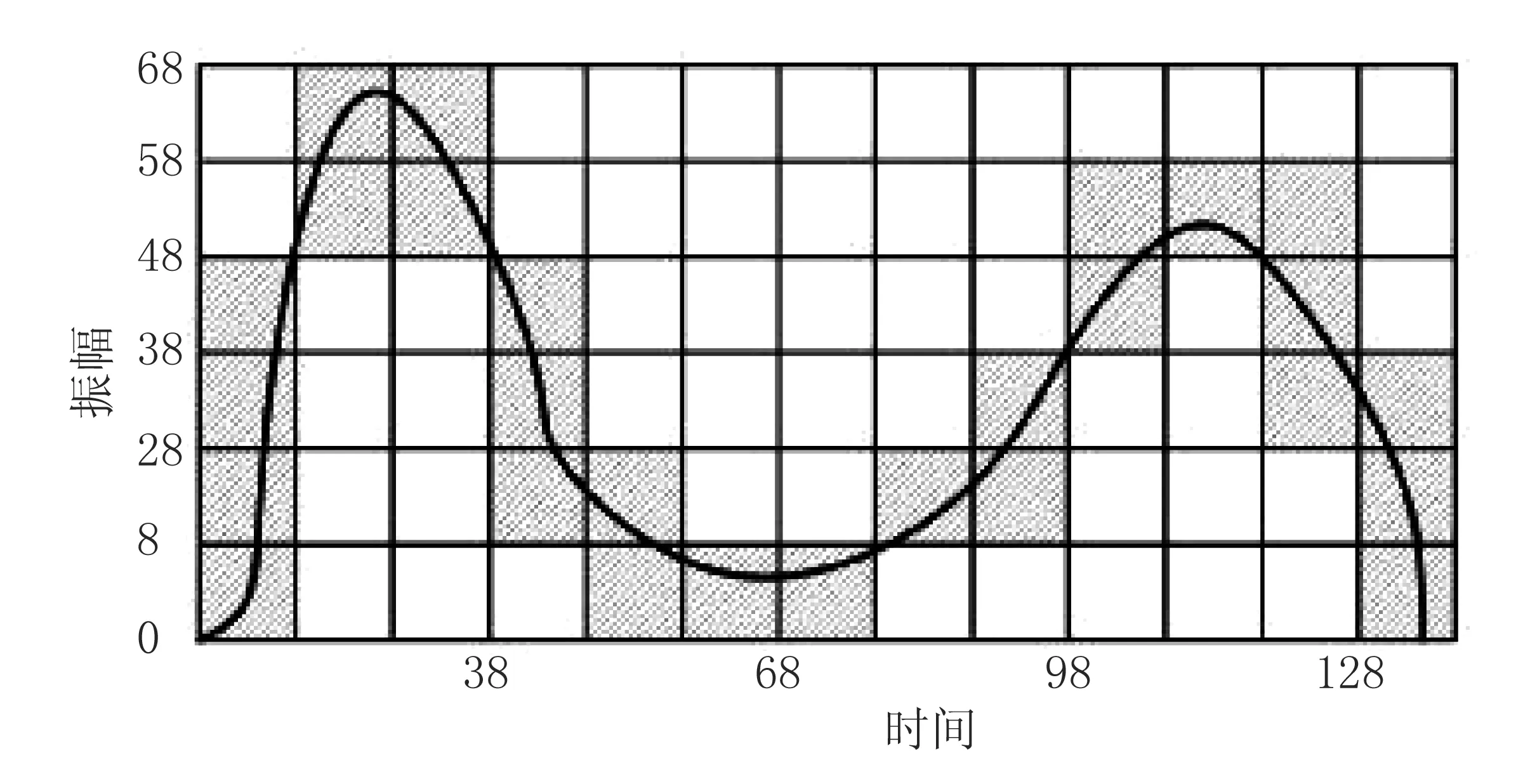
图2 δ下r(n)的盒维数

然后覆盖r(n)的方格数Nδ(r)就可计算出来.理论上，r(n)的盒维数dimBr(n)可用式(5)来计算.但由于离散信号r(n)的最高分辨率为间隔δ，所以式(5)的极限无法根据其定义δ→0求出.实际计算一般采用近似方法，即将δ网格逐步放大为kδ网格，k∈Z+.定义M(kδ)为格子宽度是kδ的离散空间上集合的网格计数，它可由下式求得：

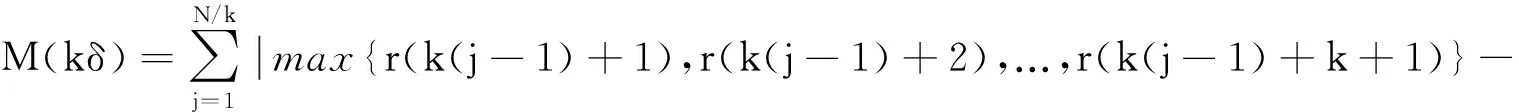
min{r(k(j-1)+1),r(k(j-1)+2),...r(k(j-1)+k+1)}|,k=1,2,…K;Klt;N

(6)

则信号r(n)在宽度为kδ的离散空间上集合的网格计数Nδ(r(n))为：

Nδ(r)=M(kδ)/kδ+1

(7)

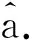
设矩形网格的最小宽度和高度分别为δw和δh，M(kδw)为r(n)在区间(jkδw,(j+1)kδw)的分段网格计数，其中j=1,2,…N0/k，其算法同式(6)，当网格高度为δh时，计算信号s(t)的网格计数Nδ(s)的式(7)可改进为：

Nδ(s)=M(kδw)/kδh+1

(8)

为检测LZ复杂度和盒维数对干扰样式的分类能力，对宽带干扰、扫频干扰、单音干扰、多音干扰、窄带干扰、脉冲干扰、QPSK信号每种干扰样式随机产生JSR(干扰信号比) = 7 ～ 15dB的100个样本，其LZ复杂度和盒维数按式(4)和式(8)进行计算，考察其均值和方差，见表1.

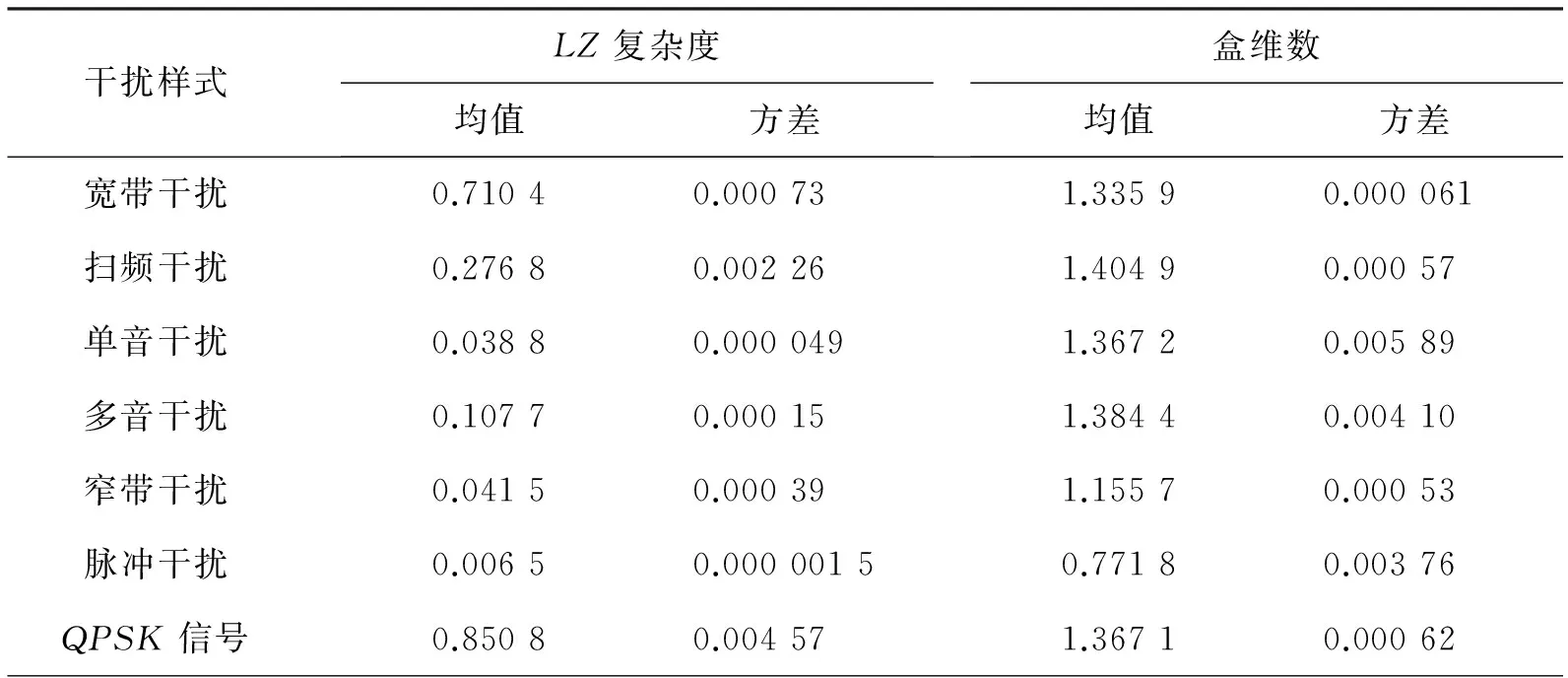
表1 常见干扰样式的LZ复杂度和盒维数比较

从表1可以看出，LZ复杂度和盒维数对几种常见的干扰样式具有良好的分类能力.LZ复杂度和盒维数可以作为常见干扰样式识别和分类的特征参数.

2.2基于指数距离的分类识别方法

从表1可以看出，干扰样式虽然是确定的几种类型，但由于干扰本身的参数不同、干信比不同等导致了每种干扰样式的特征参数分布的区域与形状差异较大，难以严格界定每种干扰分布的区域边界，这就使得对干扰的识别具有模糊性.因此，以某个中心点代表某一干扰样式的分布显然不够合理.因此采用了指数距离函数.具体表达式如下[8]：

(9)

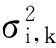
在本算法中，特征参数共有两个，故K=2.可以看出，这种指数距离函数计算方法不仅考虑到了样本与分类中心距离的影响，还考虑到了训练样本特征参数分布的方差对分类和识别的影响.该隶属度函数简单明了，不需要权重确定、相关矩阵计算等复杂运算.计算待分类样本Z与各干扰样式的指数距离后，就可按最小距离原则对Z进行分类，如下式所示：

Z=Zj,j={i|min(μi),i=1,…NJ}

(10)

式中Zj为第j种干扰样式；NJ为干扰样式种类.

综上所述，干扰样式识别框图如图3所示.对接收信号进行RF处理后，分别计算样本的波形参数和偏斜度.在进行干扰样式识别前，需要对每种干扰样式选用少量(100个左右)的样本进行参数训练.通过训练，计算每种干扰样式特征参数的均值和方差.训练完成后，就可使用式(9)计算待识别样本的指数距离，并按式(10)对样本进行识别.可以看出，与已有方法相比，本节提出的方法识别干扰样式的种类较多，识别过程简洁清晰，计算复杂度较低.

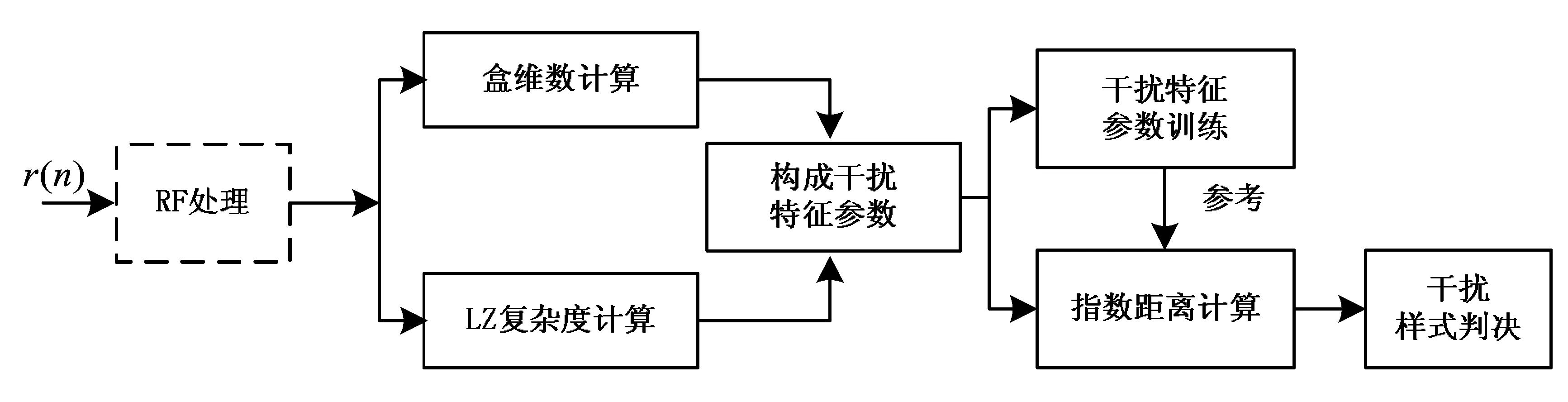
图3 基于复杂性测度的干扰样式识别框图

3 仿真结果

在仿真中，假设无线环境中存在QPSK通信信号，其载波频率为5 MHz，通信速率为100 kbit/s，单音干扰的中心频率在4～6 MHz之间随机变化.多音干扰以5MHz为中心频率，频率点数在2～10之间随机变化，频点分布在1～9 MHz之间随机取值，并进行功率归一化处理.宽带噪声干扰用高斯白噪声代替.窄带干扰由高斯白噪声通过窄带滤波器产生，中心频率为5 MHz，带宽在100～500 kHz之间随机变化.脉冲干扰的占空比在0.001%～0.01%间变化.扫频干扰的中心频率为5MHz，扫频带宽在5 MHz，4 MHz，3 MHz，2 MHz中随机选择.每个样本使用50 ms的接收信号即105个抽样数据作为识别数据.

每种干扰样式产生干信比在-7～15dB之间随机变化的40 000个含有通信信号的样本作为待识别样本测试识别率.为便于仿真，改变干信比时，保持通信信号功率不变，改变干扰的功率.单音、多音、窄带、宽带、扫频、脉冲以及仅有QPSK通信信号的识别性能，如图4所示.

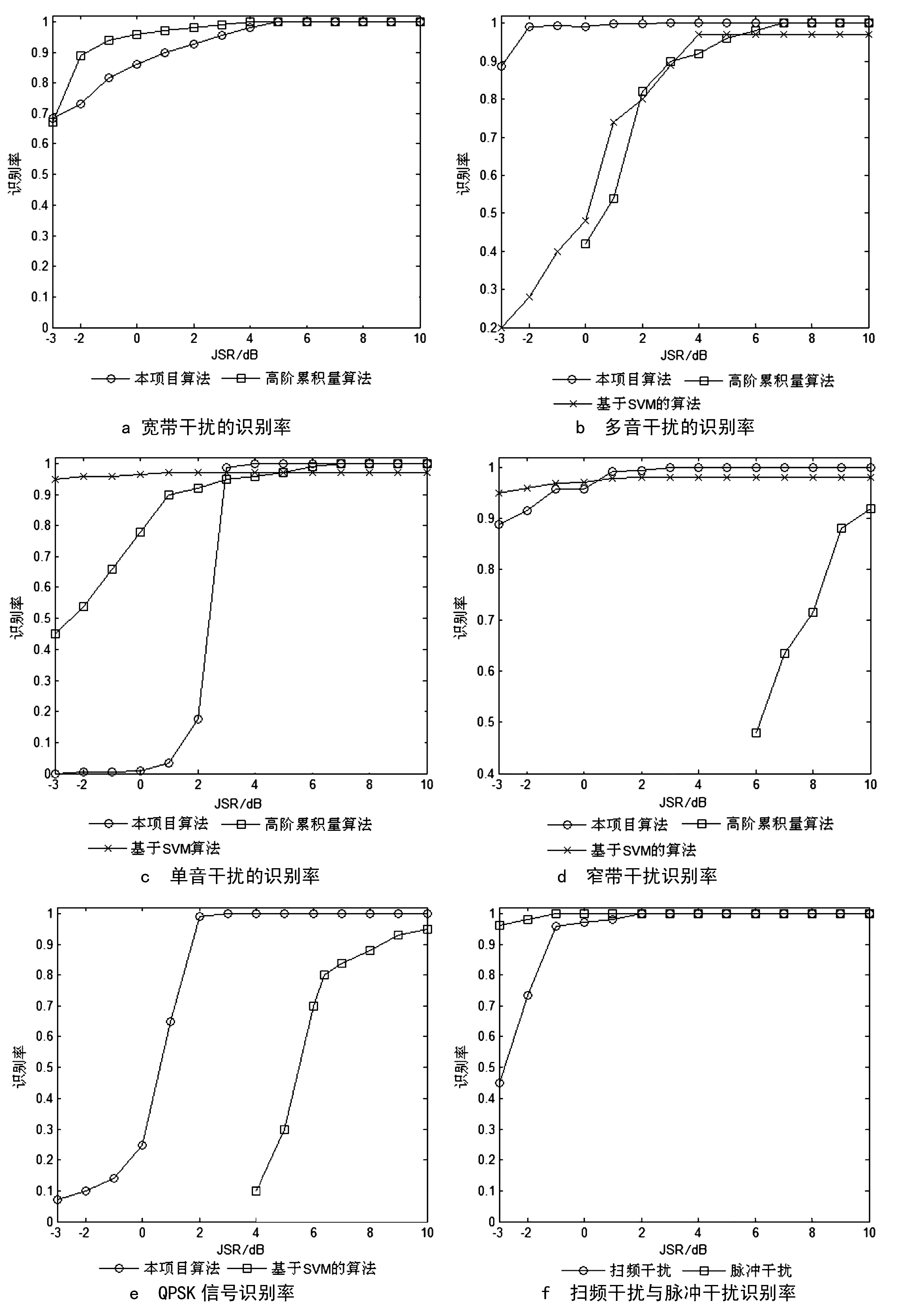
图4 JSR对干扰识别概率的影响

图4a显示，本节提出的算法在JSR ≥ 2dB时对宽带干扰具有较好的识别性能.相比之下，基于高阶累积量的算法比本节提出的算法性能略好.图4b显示在JSR ≥ -3dB时对多音干扰具有更好的性能.相比之下，基于高阶累积量的算法和基于SVM的算法性能随JSR下降而下降较快.图4c显示在JSR ≥ 3dB时对单音干扰具有较好的识别性能，这一性能比基于高阶累积量的算法和基于SVM的算法性能要差.图4d显示当JSR ≥ -3dB时，本节提出的算法性能较好.而基于SVM的算法比本文算法性能略差.图4e 显示了在无干扰而仅有QPSK通信信号时的识别性能.图4f显示了当前文献中还未研究的扫频干扰和脉冲干扰的识别性能.可以看出，当JSR ≥ -2dB时所提算法对扫频干扰的识别率超过95%，在JSR ≥ -3dB时对脉冲干扰的识别率超过90%.

4 结束语

本文提出了一种基于信号功率谱统计参数的模糊干扰样式识别方法.该方法利用接收信号功率谱的波形参数和偏斜度作为分类的特征参数；利用指数模糊度隶属函数计算待识别样本的隶属度，按最大隶属度原则来对干扰样式进行识别.与已有方法相比，本文提出的方法识别干扰样式的种类较多，识别过程简洁清晰，计算复杂度较低，有利于实际应用.仿真结果表明，该算法对于常见的六种干扰样式具有较高的识别率.

[1]Poisel R A. Modern Communication Jamming Principles and Techniques[M]. Norwood: Artech House, 2004.

[2]姚富强. 通信抗干扰工程与实践[M]. 北京: 电子工业出版社, 2012.

[3]吴昊，张杭. 基于高阶累积量与神经网络的干扰识别算法[J]. 军事通信技术,2008, 29(1): 67-71.

[4]吴昊，张杭，路威. 一种面向卫星频谱监测的复合式干扰自动识别算法[J]. 系统仿真学报, 2008, 20(17): 4681-4684.

[5]杨小明，陶然. 直接序列扩频通信系统中干扰样式的自动识别[J]. 兵工学报, 2008, 29(9): 1078-1082.

[6]Zhiyu Z, Hao C, Ningning L. Automatic Recognition of Multiple Interferences and Signals in the Same Channel Based on ICA[C]. Guilin: IEEE, 2009.

[7]孙即祥. 现代模式识别[M]. 北京: 高等教育出版社, 2008.

[8]Lempel A, Ziv J. On the complexity of finite sequences[J]. IEEE Trans. Inform. Theory, 1976, IT22(1): 75-81.

ARecognitionMethodofNovelJammingBasedonComplexityMeasurement

ZHANG Xing-zhe

(School of ECE, Mapua Institute of Technology, Manila, Philippines)

A novel jamming recognition method based on complexity measure of

signal was proposed. The proposed algorithm exploited the LZ complexity and box dimension of received signal as classified characters of jamming pattern. After the mean center and variance of each jamming pattern were calculated by some jamming samples, exponential distance function was used to calculate the distance of recognizing sample. Finally, the jamming pattern of sample was recognized by the minimum distance principle. The simulation results show that the proposed algorithm can recognize common six jamming patterns and QPSK signal accurately.

LZ complexity; mean center; variance; jamming pattern

1673-2103(2013)05-0030-07

2013-09-02

张兴哲(1989-), 男， 山东泰安人，菲律宾麻波亚理工学院， 研究方向：电子与通讯.

TN92

A