基于稳定张力的光纤绕制系统建模与仿真

赵金才，王 中，高 卓，汤伟江

(1.中国船舶重工集团公司 第七〇五研究所，陕西 西安710075;2.水下信息与控制重点实验室，陕西 西安710075)

0 引 言

张力控制系统是工业生产过程中的一种常用控制环节，广泛应用于各种自动化水平较高的生产线上，如线缆纺织、造纸、印染等行业。随着控制技术的发展和对优质产品质量的渴求，稳定张力控制成为最理想的选择。所谓稳定张力控制即指材料在处理过程中，其张力波动范围较小，且能抑制外来干扰引起的张力突变，从而实现的稳定张力控制过程［1］。由于光纤材料的特殊性，使得对张力的控制要求更为严格。若不能有效控制张力波动，将降低绕制产品的储藏寿命，同时影响光纤的信息传输能力。理论分析表明，光纤绕制时其稳态张力波动应控制在5%以内，因此，需对光纤绕制稳定张力控制系统进行结构设计及建模仿真。

1 系统介绍

1.1 系统组成

稳定张力光纤绕制机构简图如图1所示。

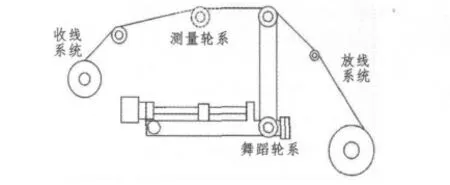
图1 稳定张力的光纤绕制机构示意图Fig.1 Structure diagram of the stable tension control system

该机构由收线系统、放线系统、舞蹈轮及测量轮系组成。工作时，原始光纤由放线系统放出，经舞蹈轮和测量轮系的传递到达收线系统，经过速度与位置的匹配处理将光纤精密均匀缠绕于收线盘上。

1.2 稳定张力控制的实现

在实现稳定张力控制时，舞蹈轮为核心控制部件，其一端通过转轴与角度传感器相连并同轴固定在机构上，另一端同心安装多个转动轮，且能绕转轴自由转动。光纤依次绕过各转动轮后与收、放线盘相连。系统启动前，通过调整设定张力值将舞蹈轮稳定在零位位置。启动后，收线系统首先响应，带动舞蹈轮转角向上转动，使线上张力瞬时增大，放线系统根据力矩平衡调整放线电机转矩输出，加快放线速度使舞蹈轮向下运动，线上张力减小，再次调整放线电机输出转矩，如此往复直至收、放线速度匹配，转角稳定在零位附近，从而使线上张力波动趋于稳定。

可见，通过控制舞蹈轮转角变化可对绕制张力波动进行控制;光纤多次绕过舞蹈轮系，可使转角变化趋于平缓，从而进一步降低光纤绕制张力的波动。

2 建立系统模型

2.1 模型建立条件

在模型建立前需进行适当假设对模型进行简化。

1)假设在绕制过程中，光纤与轮系之间没有相对滑动，收、放线之间各段光纤上的张力相等［2］;

2)假设光纤在绕制时，未产生弹性变形，即认为在其长度和径向上均未发生形变。

2.2 稳定张力控制系统数学模型

根据图1，简化相关结构，建立收、放线电机与舞蹈轮系的运动简图(如图2所示)，通过动力学分析可建立稳定张力控制的数学模型［3］。

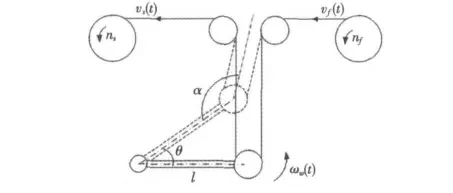
图2 稳定张力控制系统运动简图Fig.2 General diagram of the stable tension control system

1)速度关系模型

设舞蹈轮以角速度匀速ωw(t)转动θ 角，此时，可建立系统收、放线速度与舞蹈转速之间的关系为

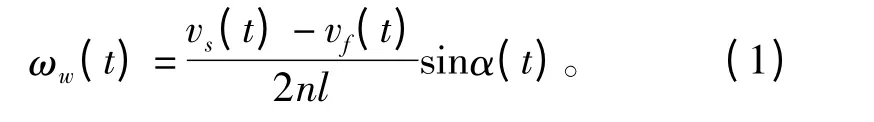
式中:vs(t)为收线线速度，m/s;vf(t)为放线线速度，m/s;n 为舞蹈轮上传动轮个数;l 为舞蹈轮摆臂长度，m;α 为舞蹈轮摆臂与收、放线速度方向夹角，(°)。

2)放线系统转矩平衡模型

对放线盘进行受力分析并结合直流电机方程得放线系统的转矩平衡模型为［4］

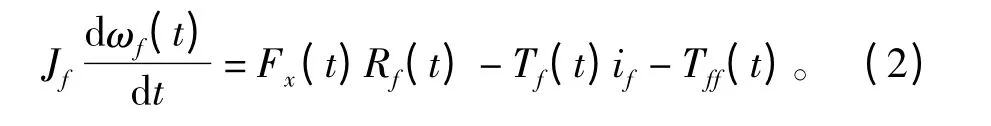
式中:Jf为放线系统转动惯量，kg·m2;ωf(t)为放线盘转动角速度，rad/s;Fx(t)为线上实时张力，N;Rf(t)为放线盘实时半径，m;Tf(t)为放线电机电磁转矩，N·m;if为放线系统所选减速器减速比;Tff(t)为放线系统的摩擦转矩，N·m。

3)舞蹈轮转矩平衡模型

根据舞蹈轮转矩平衡，可得舞蹈轮机构转动模型为

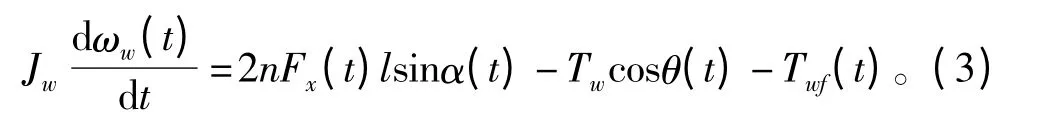
式中:Jw为舞蹈轮转动惯量，kg·m2;Tw为舞蹈轮重力矩，N·m;Twf(t)为舞蹈轮的摩擦转矩，N·m。

4)传感器输出模型

根据舞蹈轮的转角偏置引起电压的变化来控制放线电机的输出转矩，即将传感器的输出转角解算出反馈电压:

式中:k 为对应输入转角的比例系数，V/(°)，θ 为传感器输入转角。

式(1)～式(4)即组成稳定张力控制系统数学模型。

3 控制算法设计与仿真

3.1 控制算法选择

在稳定张力光纤绕制系统中，将角度传感器测量舞蹈轮的转角变化θ 引入反馈系统，控制绕制过程中的张力变化。采用增量PID 控制算法［5］，对放线电机进行控制，算法如下:

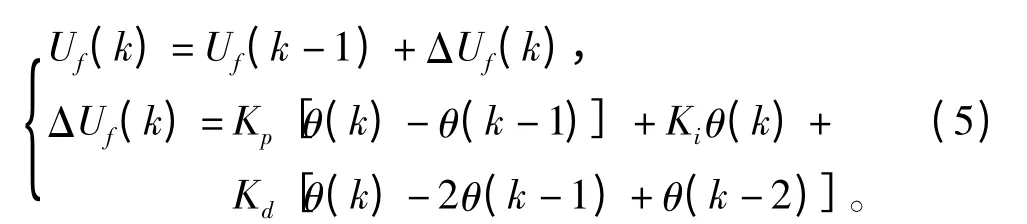
式中:Uf(k)和ΔUf(k)分别为第k 控制周期放线电机的输入控制电压及其增量，V;Kp，Ki，Kd分别为比例、积分和微分系数;θ(k)为第k 控制舞蹈轮的转动角度，(°)。

增量式PID 控制算法程序流程图如图3所示。

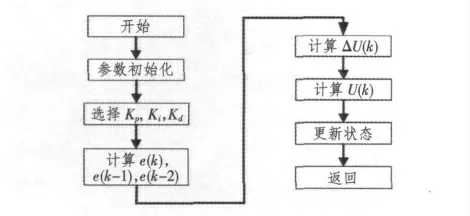
图3 增量式PID 控制算法程序流程图Fig.3 The flow chart of increment PID algorithm

3.2 算法仿真分析

PID 控制的结构简单，加权系数Kp，Ki 和Kd都有明确的物理意义［6］。在PID 参数综合调试时，比例起主要调节作用，起主导作用;积分起辅助调节作用;微分起补偿作用。按照这一原则选择控制参数Kp=2，Ki=0.1，Kd=6 对模型进行仿真并与实际系统输出结果进行对比，得输出转角和线上张力分别如图4 和图5所示。

通过2 组曲线对比可见，仿真与试验曲线的变化趋势基本一致，但试验曲线相对滞后且波动剧烈，这是由于实际系统的惯性和随机扰动所致;启动时的误差是忽略系统轮系的摩擦、转动惯量等因素所致。

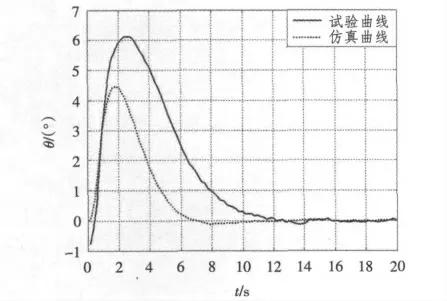
图4 转角θ 的仿真曲线与试验曲线对比Fig.4 Curve compare for angel θ

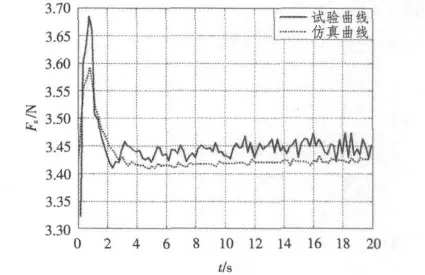
图5 张力Fx的仿真曲线与试验曲线对比Fig.5 Curve compare for tension Fx

3.3 改进算法仿真分析

在第3.2 节仿真对比曲线中，稳态张力波动为1.55%，满足系统5%的稳态控制要求，但启动阶段的张力波动较大为6.68%;要进一步提高系统的动态品质需对算法进行改进，降低启动过程的张力波动。

由于张力的变化与转角输出变化相关，通过对不同转角设计不同参数控制转角的变化，进而降低启动时张力的变化量。故采用分段PID 控制方式对不同的转角变化范围进行控制。将转角变化分为以下3 个区域:

1)稳态区域，即|θ|≤P1，其中常数P1的大小主要取决于系统对稳态精度的控制要求，P1值越小，对应的控制精度越高;

2)过渡区域，即P1＜|θ|≤P2，指舞蹈轮工作在稳态与限制区域之间过渡过程中;

3)限制区域，即|θ|≥P2，其中常数P2大小主要取决于对系统安全余量的考虑，转角超过P2即进入限制区域，此时应对转角采用快速抑制措施，避免因转角过快的变化引起张力突变从而影响绕制系统安全，P2越小，可控的安全余量越多。

对稳态区域的设计参数Kp=3，Ki=0.15，Kd=9;过渡区域的设计参数Kp=6，Ki=0.3，Kd=30;限制区域的设计参数Kp=10，Ki=0.33，Kd=50。参数的选择依据角度变化的情况，角度越大，选择的误差及超调控制越强。C1和C2的大小依据实际角度的变化范围而定。

与此同时，对收线电机采用延缓启动时间来控制放线对收线的速度跟随，使收放线的速度变化稳定，转角变化平缓;对不同收线速度设定不同的步进控制量，进一步平滑速度的突变，最终降低系统启、制动时的张力波动。如令Q1＜Q2＜Q3为给定的收线速度，对3 个不同速度采用不同步进量控制:

1)当收线速度小于Q1时，选择步进量为R1;

2)当收线速度小于Q2时，选择步进量为R2;

3)当收线速度小于Q3时，选择步进量为R3。

其中，R1＞R2＞R3，即速度越大，步进量越小。通过上述算法对系统进行仿真并与实际试验结果对比得系统输出转角及张力变化曲线分别如图6和图7所示。

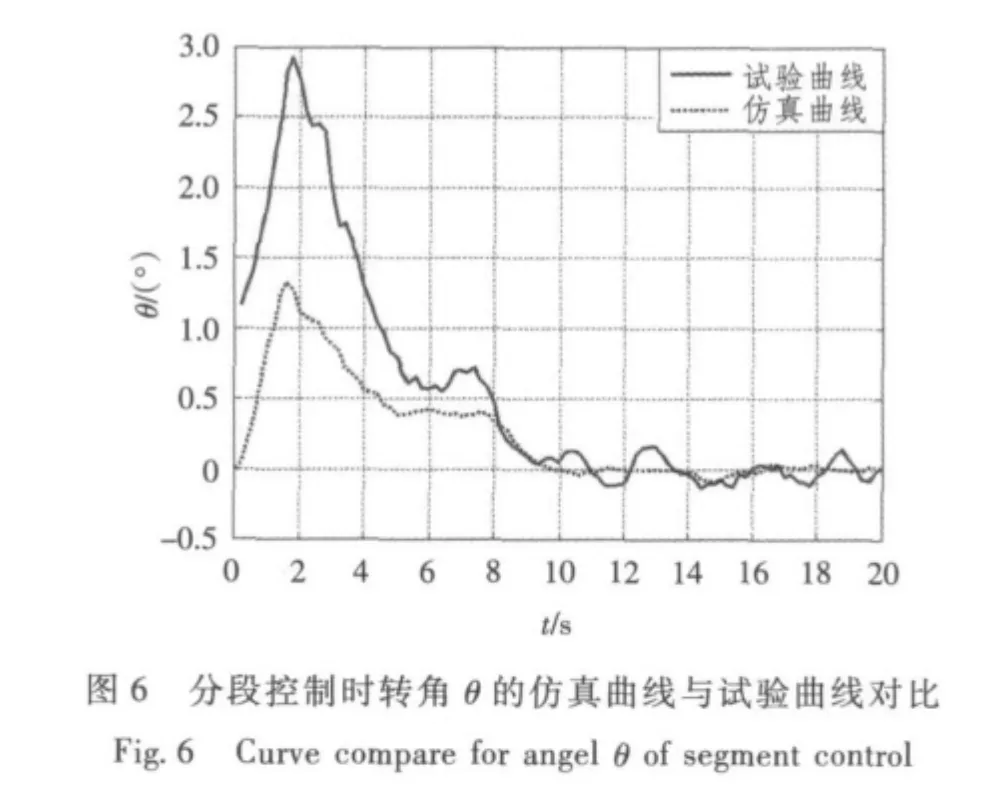
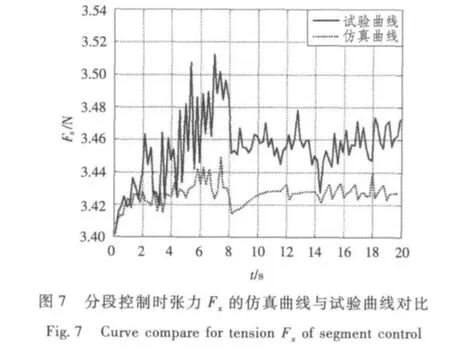
通过对比分析可见，采用分段控制和延迟收线系统启动时间，能有效降低转角和张力在启动阶段的变化量，同时满足稳态时张力变化的要求。启动阶段张力超调量仅为2.13%，稳态张力波动为1.84%，且仿真与试验曲线变化趋势基本一致。

4 结 语

依据稳定张力这一主要技术指标设计的光纤绕制控制系统，通过建模与仿真分析表明，利用控制舞蹈轮的转角变化来控制线上张力波动这一方法可行。采用增量PID 控制算法，能将稳态张力波动控制在2%以内，满足系统5%的稳态张力波动要求，有相对较高的控制精度;启动时超调是因忽略系统转动惯量等因素所致。通过延长收线速度启动达到时间和转角分段控制方式后，可进一步降低系统启动阶段的超调量，同时满足稳态张力波动要求，达到预期的控制目标。

［1］柳贺.模糊免疫自适应PID 控制在恒张力控制中的应用［D］.合肥:合肥工业大学，2007.1-2.

［2］孙冬，马保吉.光纤缠绕张力控制系统模型建立［J］.弹箭与制导学报，2006，26(2):777-780.

SUN Dong，MA Bao-ji.The modeling of tension control system in optical fiber automatic winding［J］.Journal of Projectiles;Rockets;Missiles and Guidance，2006，26(2):777-780.

［3］Ku Chin Lin.Observer-based tension feedback control with Friction and inertia compensation［J］.IEEE Transaction on Control System Teehnology，2003，11(1):109-118.

［4］高钟毓.机电控制工程［M］.北京:清华大学出版社，2011.54-58.

［5］刘金昆.先进PID 控制及Matlab 仿真［M］.北京:电子工业出版社，2011.18-25.

［6］薛定宇，陈阳泉.基于MATLAB/Simulink 的系统仿真技术与应用［M］.北京:清华大学出版社，2011.175-198.