尾舵独立控制的潜艇垂直面运动仿真

颜 俐，许 建，马运义

( 中国舰船研究设计中心，湖北 武汉430064)

0 引 言

潜艇在水中的空间运动，在弱机动时可分解成2 个平面运动，一是潜艇在水平面的运动，这时与水面船舶在水面上运动一样，主要研究航向的保持与改变，而不涉及深度的变化;二是艇在垂直面的运动，主要研究纵倾和深度的保持与改变，而不涉及航向的变化。能够在垂直面运动，是潜艇区别于水面舰船的一个重要方面，也是潜艇能够充分发挥其战术性能的重要保障。因此，对潜艇垂直面运动规律进行研究显得尤为重要［1-5］。

众所周知，降低潜艇的自身噪声可有效增加声呐的探测距离，利用双舵对潜艇进行控制其噪声要比利用单尾舵控制大得多。而且由于声呐都位于潜艇的首部，因此在低噪声航行工况下让围壳舵保持在零位，可以消除围壳舵对周围流场的扰动，消除了舵运动击水时的水动力噪声，同时围壳舵机也处于关闭状态，消除了机械噪声、管路油压冲击噪声和器件摩擦噪声。因此单尾舵控制可以达到局部降噪的效果，从而在一定程度上增加了声呐的探测距离。

另外出于对潜艇操纵安全性考虑，一般潜艇尾舵都在螺旋桨之后，尾舵在桨后受到螺旋桨排出流的作用，使舵效明显增强。而且潜艇尾舵离潜艇中心较围壳舵远，因此与围壳舵相比，尾舵的优点是力臂大，舵效好，控制力强，操纵尾舵容易造成纵倾或恢复纵倾。此外尾舵具有比围壳舵大的面积和展舷比，可提供较大的升力。这是之所以采用单尾舵控制而不采用单围壳舵控制的原因。

综上所述，单尾舵控制在潜艇低噪声航行工况下具有很大的优势，能在一定程度上降低潜艇的自噪声和辐射噪声，提高潜艇的隐蔽性和战斗性能。因此本文采用单尾舵控制方案以进一步降低潜艇噪声。

1 模糊控制方案的设计

由于单尾舵控制潜艇，要同时兼顾控制潜艇的纵倾和深度。如果只设计1 个控制器，则控制的输入有4 个:深度偏差Δξ=ξz-ξ，偏差变化率γ=dΔξ/dt，纵倾偏差Δθ=θz-θ 和偏差变化率κ=dΔθ/dt，这容易造成模糊控制器的结构复杂，规则库庞大，影响解模糊的效率。潜艇在深度机动的过程中，一般先是把纵倾控制到指定纵倾，当纵倾到达指令纵倾后，再根据当前深度偏差把深度控制到指定深度。因此本文将采用2 个模糊控制器，1 个控制器通过操纵尾舵来控制纵倾，另1 个控制器则通过操纵尾舵来控制深度。深度机动开始阶段，先由纵倾控制器把潜艇纵倾控制到指令纵倾，当到达指令纵倾后，控制切换到深度控制器，通过当前深度偏差把深度控制到指令深度。由于潜艇自身具有扶正力矩，因此在深度控制的同时，扶正力矩会把纵倾拉到0 纵倾。其结构图如图1所示。

图1 单尾舵模糊控制结构图Fig.1 Fuzzy control structure of single stern-rudder

2 深度模糊控制器的设计

深度模糊控制器选用二维的模糊控制器［6-11］，控制器的输入深度偏差Δξ=ξ2-ξ 和深度偏差变化率γ=dΔξ/dt。深度偏差变化率是一个微分信号，而潜艇的深度偏差变化率是不能直接通过传感器得到的，而是通过深度偏差微分得到的数字量，因此要得到微分量还需要加入微分器。在经典调节理论中，采取直接微分的方式得到深度和纵倾的一阶微分量，也是常用的处理方法之一。但是经典微分器在微分被随机信号污染的信号时就会出现放大污染噪声，从而使出来的微分信号产生毛刺和抖动。通过数学推导可以得到，输出信号y(t)是输入信号v(t)的微分信号叠加上放大了1/T 倍的噪声信号，而时间常数T 很小，因此噪声放大很严重，有时完全可以淹没微分信号，所以经典微分环节对噪声有严重放大效应。因此，在微分处理过程中要避免将一个状态变量微分产生另一个状态变量。由于上述原因，本文将采用新型的跟踪微分器。最速非线性跟踪微分器能很好地克服噪声放大效应的二阶及高阶微分环节。最速非线性跟踪微分器［12-13］的算法公式可表示为

输出方程为

其中:

将深度信号ξ 作为输入，可分别得到经典微分器和最速非线性跟踪微分器的微分信号。

图2 两种微分器的信号比较Fig.2 Signal comparison of two differentiators

从图2 可以看出，经典微分器出来的微分信号抖动非常明显甚至失真，而最速非线性跟踪微分器出来的微分信号非常平滑，同样在设计纵倾控制器和航向控制器时都可以采用最速非线性跟踪微分器得到纵倾和航向的微分信号。从而在很大程度上提高模糊控制器的控制效果。

2.1 论域及基本论域

深度偏差Δξ=ξz-ξ 的论域取为［-10，10］，深度偏差变化率γ=dΔξ/dt 的论域取为［-2，2］，而控制量尾舵角的δs论域设为［-6，6］。根据实际情况，控制系统中选择深度偏差的基本论域为［-100，100］，深度偏差变化率的基本论域为［-2，2］，尾舵角的基本论域为［-30，30］。

2.2 量化因子和比例因子

在论域和基本论域确定的情况下，量化因子和比例因子即可确定如下:

1)深度偏差量化因子

2)深度偏差变化率量化因子

3)输出比例因子

2.3 模糊语言变量和隶属度函数的确定

模糊控制器的输入输出语言变量设为5 个，分别为{负大(NB)，负小 (NS)，0 (ZE)，正小(PS)，正大(PB)}。

根据所取的模糊语言变量可以得到深度偏差、偏差变化率和尾舵角各模糊子集的隶属度函数如图3 ～图5所示。

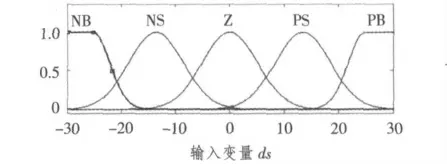
图5 尾舵角δs的隶属度函数Fig.5 Membership function of stern-rudder δs

2.4 模糊规则的确定

深度控制器模糊规则的获取包括潜艇控制工程理论知识、专家意见、实际操作经验。对于深度机动时的潜艇操纵而言，操舵人员的实践经验非常重要，一般根据实际操作过程来设计模糊规则。在深度机动过程中可以根据典型的阶跃响应来指定模糊规则。

图6 潜艇深度机动控制过程的典型阶跃响应Fig.6 The classic step response of submarine maneuvering

图6 描述了潜艇深度机动过程的典型阶跃响应，刚开始时，即在a 点附近，深度偏差Δξ 很大，而深度偏差变化率γ 很小，这时主要是为了消除深度偏差，因此需要一个大的舵角信号使潜艇快速变深以减小偏差。所以在a 点附近的规则为:如果深度偏差Δξ 是PB 且γ 是ZE 或NS，则尾舵角δs为NB(负大)。

在图6 中的b 点附近，此时的深度偏差Δξ 很小，而偏差变化率γ 比较大，这时要防止系统产生超调甚至振荡，因此需要一个正小的控制信号以避免实际深度超调过大。所以在b 点附近的规则为:如果深度偏差Δξ 是NS 或ZE 且γ 是NB，则尾舵角δs为PS (正小)。

在点c 和d 附近的控制行为分别与点a 和b 附近的相似。利用这样的思路可以总结出模糊控制器根据Δξ 的值和γ 的值对δs模糊规则:当Δξ 较大时，应当取较大的尾舵角，为了快速消除深度偏差，此时深度偏差Δξ 在控制器中占主导地位。当Δξ 中等大小时，为防止较大超调，应适当减小尾舵角以免产生大的超调。当Δξ 较小而γ 较大时，这时偏差很小而主要任务是防止大的超调或是振荡，这时γ 占主导地位，这是尾舵角应压反舵。而压反舵的时机要把握好，太早影响动态过程使深度机动过程慢，太晚产生超调且反舵角大。因此这种情况下应根据仿真反复调试找出合适的规则。

根据潜艇深度机动过程的典型阶跃响应可以得到Δξ，γ 和δs的模糊规则库，其规则如表1所示。

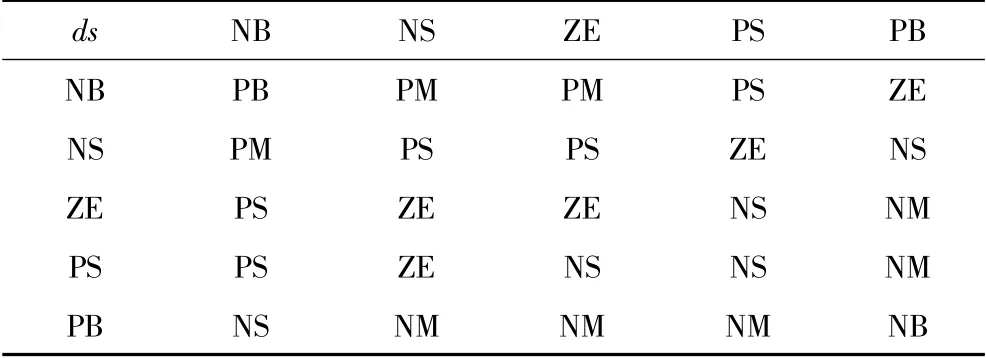
表1 Δξ，γ 和δs的模糊规则库Tab.1 Fuzzy rule base of Δξ，γ and δs

利用Matlab 模糊工具箱可以看到所设计的模糊控制器的性能好坏，可以利用工具箱输出各语言变量的模糊推理特性曲面，如图7所示。

图7 Δξ，γ 和δs的模糊推理输出特性曲面Fig.7 Fuzzy reasoning surface of Δξ，γ and δs

从图7 可以看出，Δξ，γ 和δs的模糊推理输出特性曲面过渡平滑，没有突变。由此可知，该控制系统的模糊控制规则选择合理。

2.5 模糊推理和解模糊

模糊推理机是模糊控制系统的核心，根据模糊输入和模糊控制规则，模糊推理机求解模糊关系方程，获得模糊输出。

控制系统中采用的模糊推理机主要有乘积推理机、最小推理机、Zadeh 推理机、LukasieWicz 推理机和Dienes-Rescher 推理机等。在本文中的深度机动控制系统中采用Mamdani 极小运算。

通过模糊推理机得到的是模糊量，而对于实际的控制必须为非模糊量即清晰量，因此需要将模糊量转换成清晰量，并将表示在论域范围内的清晰量经尺度变换变成实际的控制量。将模糊的控制量经清晰化计算变换成表示在论域范围内的清晰量是通过解模糊器来完成的，本文采用中心解模糊方法，则模糊控制器的输出为

其中:y*为输出的尾舵角;为深度偏差Δξ 和偏差变化率γ 的隶属度函数的中心点，其中心点在上述的隶属度函数中获取;为深度偏差Δξ 和偏差变化率γ 的隶属度函数。

3 纵倾模糊控制器的设计

3.1 论域及基本论域

纵倾偏差Δθ=θz-θ 的论域取为［-2，2］，纵倾偏差变化率κ=dΔθ/dt 的论域取为［-1，1］，而控制量尾舵角的δs论域设为［-6，6］。根据实际情况，控制系统中选择纵倾偏差的基本论域为［-10，10］，纵倾偏差变化率的基本论域为［-1，1］，尾舵角的基本论域为［-30，30］。

3.2 量化因子和比例因子

在论域和基本论域确定的情况下，量化因子和比例因子即可确定如下:

1)纵倾偏差量化因子

2)深度偏差变化率量化因子

3)输出比例因子

3.3 模糊语言变量和隶属度函数的确定

模糊控制器的输入输出语言变量设为7 个，分别为{负大(NB)，负中(NM)，负小(NS)，0(ZE)，正小(PS)，正中(PM)，正大(PB)}。根据所取的模糊语言变量可以得到纵倾偏差、偏差变化率和尾舵角各模糊子集的隶属度函数如图8 ～图10所示。

图8 纵倾偏差Δθ 的隶属度函数Fig.8 Membership function of trim deviation Δθ

3.4 模糊规则的确定

根据潜艇深度机动过程的典型阶跃响应可以得到Δθ，κ 和δs的模糊规则库，其规则如表2所示。

表2 Δθ，κ 和δs的模糊规则库Tab.2 Fuzzy rule base of Δθ，κ and δs

利用Matlab 模糊工具箱可以看到各语言变量的模糊推理特性曲面，如图11所示。

图11 Δθ，κ 和δs的模糊推理输出特性曲面Fig.11 Fuzzy reasoning surface of Δθ，κ and δs

从图11 可以看出，Δθ，κ 和δs的模糊推理输出特性曲面过渡平滑，没有突变。由此可知，纵倾控制器的模糊控制规则选择合理。

3.5 模糊推理和解模糊

纵倾控制器同样采用Mamdani 极小运算，解模糊的方法采用中心解模糊，则控制器的输出

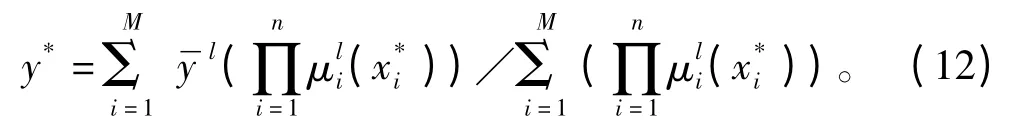
其中:y*为输出的尾舵角;为纵倾偏差Δθ 和偏差变化率κ 的隶属度函数的中心点，其中心点在上述纵倾隶属度函数中获取;为纵倾偏差Δθ 和偏差变化率κ 的隶属度函数。

4 系统仿真验证

为了验证单尾舵模糊控制器的控制效果，针对潜艇在无限深、广、静的水域中航速为8 kn 的深度机动进行了半实物仿真。

1)初始深度60 m，目标深度90 m，指令纵倾2°，舵速2.5°/s，采样时间0.2 s，仿真时间600 s。仿真曲线如图12 ～图14所示。

从仿真可以看出，深度没有超调，机动时间263 s，稳态后不存在静差。通过纵倾曲线可看到，深度机动的初始阶段纵倾在纵倾控制器的作用下到达2°指令纵倾，即44 s 时达到指令纵倾，此时深度控制器开始工作，当前深度为73.2 m，根据当前的深度偏差进行深度控制，最终深度稳定在90 m 的指令深度。在整个机动过程中围壳舵角始终为0，尾舵打舵4 次。且过渡过程平稳没有出现振荡现象。因此采用单尾舵控制在整个机动过程中，舵机打舵次数较双舵明显减少，因此可进一步降低潜艇在低噪声工况下的辐射噪声。为了进一步减小打舵噪声，可以限制尾舵的最大出舵角，限制尾舵角最大出舵角8°，舵速2.5°/s。

2)航速6 kn，初始深度60 m，目标深度90 m，指令纵倾1.5°，尾舵角最大10°，采样时间0.2 s，仿真时间800 s。

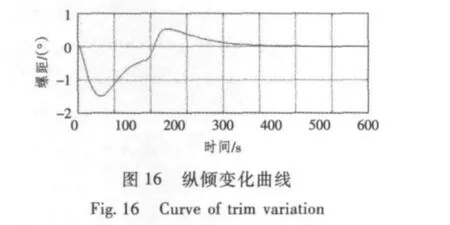
从图15 ～图17 可以看出，在限舵的情况下，深度依然没有超调，纵倾角达到指令纵倾角1.5°后在扶正力矩的作用下稳定到0。但在低航速单尾舵的情况下机动时间长，在6 kn 的航速下深度修正30 m，机动时间近300 s，对快速机动不利，但是为了降低潜艇的打舵噪声适当地牺牲下机动性能也是值得的，机动过程中舵机运行平稳，没有振荡，而且尾舵打舵次数最多没有超过4 次，从而比没有限舵的情况下进一步减小了打舵噪声，提高了潜艇的隐蔽性。

5 结 语

本文利用单尾舵模糊控制器实现了潜艇在垂直面的深度控制和纵倾控制。从仿真结果看，潜艇纵倾变化小、出舵量小、打舵次数少，表明该控制器具有较好的控制效果，能大大降低潜艇的打舵噪声和辐射噪声。

［1］施生达.潜器操纵性［M］.北京:国防工业出版社，1995.

［2］林莉.专家控制及其在船舶自动舵中的应用研究［D］.东南大学，2002.

［3］郑为民.船舶操舵系统的最优控制［D］.大连海事大学，2000.

［4］王淑瑛.浅谈潜艇操纵控制系统自动化的发展［J］.舰船导航，2004(3):39-43.

［5］杨盐生，贾欣乐.船舶航向的变结构控制自动舵设计［J］.大连海事大学学报，1998(1):14-18.

［6］王立新.模糊系统与模糊控制［M］.北京:清华大学出版社，2003.

［7］诸静.模糊控制原理与应用［M］.北京:机械工业出版社，2005.

［8］朱彤，任庆昌.PID—模糊控制的应用探讨［J］.电气传动自动化，2002，24(3):11-13.

［9］楼顺天.基于MATLAB 的系统分析与设计——模糊系统［M］.西安:西安电子科技大学出版社，2001.

［10］何平，王鸿绪.模糊控制器的设计及应用［M］.北京:科学出版社，1997.

［11］王立新.模糊系统与模糊控制［M］.北京:清华大学出版社，2003.

［12］黄一，张文革.自抗扰控制器的发展［J］.控制理论与应用，2002，19(4):485-492.

［13］韩京清.自抗扰控制技术-估计补偿不确定因素的控制技术［M］.北京:国防工业出版社，2008.