敷设去耦层水下简支撑板的振动特性

赵 军，何世平

( 海军工程大学 机械工程系，湖北 武汉430033)

0 引 言

敷设去耦覆盖层是舰艇减振降噪的一种重要措施，它可减小舰艇壳体振动向外部流体的传递，从而降低水下辐射噪声。要达到上述目的，去耦覆盖层应选择低刚度的柔性材料。一个极限的情况是，舰艇壳体与流体之间插入一个空气层，将完全隔离舰艇壳体振动向流体中的传递。在实际应用中，通常只是在舰艇表面局部敷设去耦覆盖层，但这样会产生如下问题:敷设去耦层区域的结构振动是否会增加从而增加向周边结构的传递，影响去耦覆盖层的降噪效果?为此，本文对敷设去耦层的水下结构振动特性开展了理论研究。

对于去耦层的研究，目前国内外大多数研究集中于去耦层的隔声性能。陶猛［1］等利用传递矩阵法研究了无限大板上敷设多层去耦层的隔声性能，并指出当钢板质量较大或者频率较高时，柔性层对于板本身的减振效果实际上很小。该结论的假设基础实质上是针对钢板本身的机械阻抗较大时的情况，而对于机械阻抗较小的板在敷设去耦层后在高频上的振动特性并没有给出。Alain［2］等将去耦层等效为弹性元件建立了一边为空气、一边为水的简支板在敷设去耦层后的声辐射特性。他将该模型和三维模型进行了比较，指出去耦层的剪切波对板的声辐射影响较小，因此在去耦材料较软较轻时，2 种模型在去耦层描述上一致性较好。Laulagnet［3］运用三维模型研究了有限圆柱壳在敷设去耦材料后水下的声辐射特性，提出:①在敷设去耦层后圆柱壳的振动在低频时几乎没有变化;②在高频阶段，敷设去耦层后板的振动存在放大现象。但他的重点在反共振频率上，并没有给出具体的机理性解释，也未阐明是否敷设去耦层的有限板也有上述同样的振动特性。

本文将去耦层等效为弹性元件推导了一边为空气、一边为水的简支撑钢板在敷设去耦覆盖层后的运动微分方程，并运用简正模态法推导出敷设去耦层后板的均方速度及干面均方速度插入损失。在此基础上，又分别研究了敷设不同去耦层后板的振动特性变化，以及敷设去耦层后板在不同激励频率段的振动特性。

1 理论描述

1.1 物理模型

取一嵌于无限大障板中的四边简支矩形板作为研究对象，矩形简支板表面均匀敷设去耦覆盖层，如图1所示。障板上方为水，障板下方为空气。矩形板的物理描述采用了薄板克希霍夫理论(只考虑弯曲运动)，而在去耦覆盖层的描述上将其等效为弹性元件(忽略了去耦层的剪切运动、弯曲运动及拉压运动)。

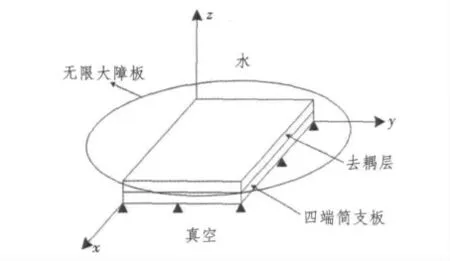
图1 浸入在水中覆盖去耦层的四端简支板简图Fig.1 Schematic representation of the baffled plate covered with a decoupling layer and immersed in water

将去耦层等效为弹性元件的假设基础是去耦层材料柔软，厚度方向变形远大于其他方向的变形。通过以上假设可将图1 中的物理模型简化为图2，图中w1和w2分别为板和去耦层表面的厚度方向位移。

图2 简化物理模型Fig.2 Simplied physical model

1.2 运动方程建立及求解

基板的运动方程写成频域形式为

相比于基板的密度，去耦层密度较小，可以忽略其质量，因此去耦层可以等效为无质量的弹性元件。此时施加在去耦层表面的声压(忽略空气对基板的声压作用)，式(1)中的未知量为板厚度上位移和声压P(Q)。

去耦层等效为弹性元件后可进一步建立去耦层表面运动和施加在去耦层表面声压作用的关系，即

式中Zc为去耦材料的阻抗。

重流体中的声压控制方程为Helmholtz 方程，即

式中:M 为流体空间的一点;k0为波数，k0=ω/c0，c0为水中的声速。

通过声压和去耦层表面法向速度的连续性可得

利用瑞利积分得出声压

式中:p0为重流体的密度;ηM为板的法向指向重流体;Q 和M 为去耦层表面上的2 点;S 为去耦层的表面;G(M，Q)为半空间格林函数，其表达式为

G(M，Q)=e-jkR(M，Q)/2πR(M，Q)。

由式(1)、式(2)和式(4)组成的方程组中仍含有3 个未知数，P(Q)。联合式(2)和式(4)化为

四端简支边界条件下为:

其中，a 和b 分别为板x 方向长度，y 方向宽度。

同理，将重流体对去耦层的声压用简正模态展开为

简正模态分布函数为

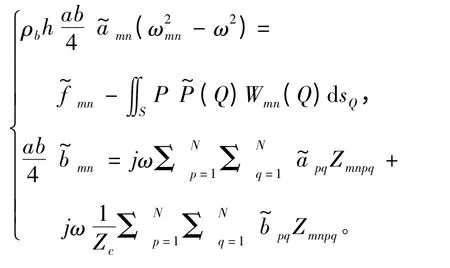
将上式写成矩阵形式得

1.3 均方速度的表达式

为了表示板表面振动情况，定义均方速度，均方速度表达式如下:

同理，定义干面均方速度插入损失表达式为

2 数值计算

取板长为1.2 m，宽为1.2 m，厚为0.009 m，板体密度取7 850 kg/m3，板的杨氏模量E=2.1*1011Pa，损耗因子取0.005;重流体为水 (ρ0=1 000 kg/m3，水中声速c0=1 460 m/s)，去耦层厚度取0.01 m，去耦层杨氏模量E 分别取106，107，108Pa。激励力采用幅值为1 N 的简谐点力激励，激励位置取坐标(0.3，0.3)，所取频率范围远低于板的临界频率，均方速度参考值为1 m2/s2(dB，re:1 m2/s2)。

将板厚度上的位移和声压按简正模态展开的收敛性需进一步研究。图3 给出了均方速度在取不同阶模态情况下的收敛性。可以看出，在最高阶模态取15 和20 时，其均方速度趋于一致，说明在最高模态数大于15 时均方速度的收敛性越好。因此所取最高模态数至少为15 数值计算才能有较好的收敛性，为保证精度在下面的数值计算中最高阶模态取20。

图3 覆盖去耦层后板的均方速度在取不同阶模态情况下的收敛性(E=108Pa，ηC=0)Fig.3 Covergence of the mean square velocity of the covered plate at different modal (E=108Pa，ηC=0)

1)未敷设去耦层的板和敷设去耦层的板均方速度的比较

图4 ～图6 分别给出了去耦层杨氏模量E 取不同值时敷设去耦层后与未敷设去耦层的基板均方速度比较。在低频段f ＜500 Hz 时，敷设去耦层后板的均方速度和未敷设去耦层的板的均方速度相差均很小;在高频段 (见图4 和图5)f ＞3 000 Hz 时，板的均方速度在敷设后相对未敷设前有明显的放大现象，并且即使在图6 杨氏模量较大(E=108Pa，ηC=0)，f ＞4 000 Hz 时，仍存在放大现象。图6 也比较了去耦层不同损耗因子下敷设去耦层后板的均方速度。可以看出，随着损耗因子的增大，敷设去耦层后板的均方速度明显减小，放大现象减弱，这主要是由于板的振动能在去耦层高损耗因子下转化为内能的部分较多。

图4 未敷设去耦层板和敷设去耦层板的均方速度比较Fig.4 Comparison of mean square velocity Between plate uncovered and covered

2)敷设去耦层的板和真空中板均方速度的比较

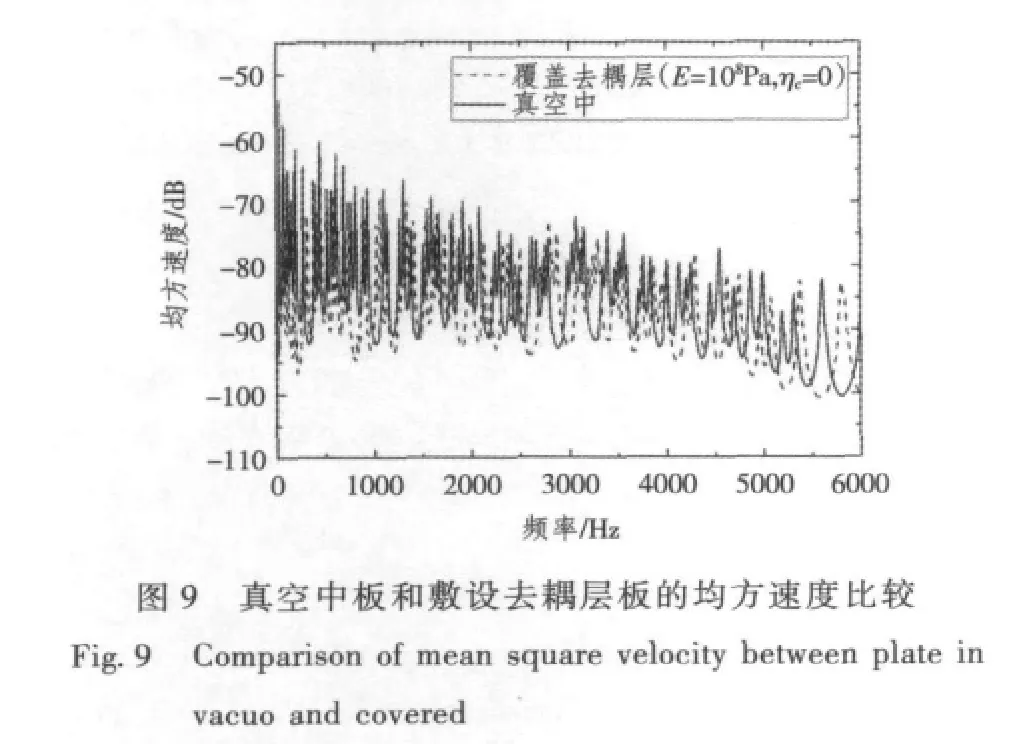
图7 ～图9 分别给出了去耦层取不同杨氏模量时敷设去耦层后板与真空中板的均方速度之比。从图7 和图8 可以看出，在去耦层杨氏模量较小时，敷设去耦层后板的均方速度逼近与真空中板的均方速度，比较图7 和图8 可以发现，在较大杨氏模量下，逼近真空的现象在更高频才能出现;而在图9中E=108Pa 时，由于截取频率上限较小，没有出现逼近真空的现象。

图7 真空中板和敷设去耦层板的均方速度比较Fig.7 Comparison of mean square velocity Between plate in vacuo and covered

3 板的振动放大现象

数值计算给出的均方速度是各阶模态加权所得结果，单从数值计算中无法解释不同频率段敷设去耦层后板的位移相应的变化，因为点激励下不同频率段，所激励出的模态是不一样的，并且模态间的耦合系数也不一样，因此需从单模态下进行研究。不失一般性取板的(m，n)阶模态。根据上文的干面均方速度插入损失的定义，推得单模态下干面均方速度插入损失为

讨论去耦层在取不同阻抗下的干面均方速度插入损失:

1)当Zc很大→∞时，可以看出

干面均方速度插入损失式(13)→0，说明在去耦层阻抗极大时，敷设了去耦层后的板单模态振动既不减小也不放大。由于(m，n)阶模态的任意给定性便可推断出任意模态在去耦层阻抗极高的情况下都符合以上结论，因此可以推断出在去耦层阻抗极大时，去耦层对板的振动既不放大也没有相应的减小作用。由于本文所采用的假设基础是去耦材料较软，因此这里Zc很大实际上指的是去耦层厚度很薄时。

2)当Zc很小→0 时，可以看出

式(13)可以化为

由式(14)可以得出在去耦层阻抗极小的情况下，敷设去耦层板的单模态均方速度逼近于真空中板的均方速度。由于(m，n)阶模态的任意给定性，可将上述结论推广至任意模态下，即去耦层阻抗极小时板的振动趋向于真空中的振动。

3)当Zc为有限值域时，需考虑频率的影响，因为C 与模态耦合系数Zmnpq相关，在不同频率上Zmnpq的性质是不一样的。

根据文献［13］的结论，在低频k0* a ＜＜1 时，自耦合系数Zmnmn的实部和虚部都很小，同样对于互耦合系数的实部虚部也是这样，因此可在低频有如下极限:C/Zc→0，插入损失就趋向于0，即在k0* a＜＜1 时，去耦层对板的单模态几乎没有任何影响。推广到任意模态，可得出在低频k0* a ＜＜1 情况下，去耦层对板的振动几乎没有任何影响。

在高频k0* a ＞＞1 时，根据文献［13］阻抗耦合系数的极限性质可知:①自耦合系数Zmnmn的实部趋向于ρ0c0，虚部趋向于0;②互耦合系数实部与虚部都趋向于0。这样对于单模态下C 就可以化简为

进一步化简式(13)，可得

根据数学不等式性质得:

即在高频u=k0* a ＞＞1 时，当频率等于真空中的模态频率时干面均方速度损失最大。由于在高频上总存在式(15)大于0，即干面均方速度损失大于0，这说明在高频总存在敷设去耦层后板振动的放大现象。当不在真空中的模态频率时，A≠0，高频时忽略掉，式(16)可进一步化简为

式(17)实际上是高频时真空中板的均方与重流体作用板的均方速度之比，该式说明了在高频去耦效果好，使板与重流体间的耦合作用越来越弱，因此敷设去耦层板的振动在高频阶段逼近于真空中板的振动。所以可以得出在Zc有限值时高频阶段(k0* a ＞＞1 )敷设去耦层板的振动总有趋向于真空中板的振动趋势。因此在高频上敷设去耦层的板在高频阶段相对未敷设的板振动是放大的。

4 结 语

1)将去耦层等效为弹性元件简化了去耦层的描述，应用简正模态法推导出敷设去耦层后板的均方速度，并分析了Zc在不同情况下的干面均方速度插入损失:在Zc极大时，去耦层对板的振动没有放大或减小作用;在Zc极小时，重流体作用下敷设去耦层板的振动等效于真空中的振动。数值计算表面在有限值时，也有上述趋势，随着Zc的增大，去耦层对板振动影响程度越来越小;随着Zc的减小，板的振动逐渐逼近于真空中板的振动。

2)在Zc有限值时，低频时k0* a ＜＜1，由于流固耦合现象较弱和去耦层效率较低的原因，去耦层对板的振动几乎没有任何影响;高频时k0* a ＞＞1，去耦层去耦效率的提高使板与重流体间的流固耦合作用越来越弱，随着频率增大板的振动逐渐逼近于真空中板的振动，因此敷设去耦层的板在高频阶段相对未敷设的板振动是放大的。随着去耦层阻尼损耗因子的增加，放大现象减弱。

［1］陶猛，汤渭霖，范军.柔性去耦覆盖层降噪机理分析［J］，船舶力学，2010，14(4):421-429.

［2］BERRY A，FOIN O.Three-dimensional elasticity model for a decoupling coating on a rectangular plate immersed in a heavy fluid［J］.J.Acoust.Soc.Am，2001，109(6):2704-2714.

［3］LAULAGNET B，GUYADER J L.Sound radiation from finite cylindrical coated shells，by means of asymptotic expansion of three-dimensional equations for coating［J］.J.Acoust.Soc.Am，1994，96:277-286.

［4］KO S H.Reduction of a structure-borne noise using an airvoided elastomer［J］.J Acoust.Soc，Am，1997，101(6):3306-3312.

［5］KELITE R F.Signal response of elastically coated plates［J］.J.Acoust.Soc.Am，1998，103:1855-1863.

［6］CRIGHTON D G.Aspects of the reflexion and free wave properties of a composite panel under fluid loading［J］.Journal of Sound and Vibration，1979，64(4):467-474.

［7］LAULAGNET B，GUYADER J L.Sound radiation from a finite cylindrical shell covered with a compliant layer.Journal of Vibration and Acoustics，1991，113:267-272.

［8］GARRISON M R，MILES R .Random response of plate partially covered by a constrained layer damper［J］.Journal of Sound and Vibration，1994，172(2):231-245.

［9］BERRY A，GUYADER J L.A general formulation for the sound radiation from rectangular，baffled plates with arbitrary boundary conditions.J.Acoust.Soc.Am，1990，88(6):2792-2802.

［10］ATALLA N，NICOLAS J.A new tool for precicting rapidly and rigorously the radiation efficiency of plate-like structures［J］.J.Acoust，Soc.Am，1994，95(6):3369-3378.

［11］缪旭弘，王仁乾，顾磊.去耦隔声层性能数值分析［J］.船舶力学，2005，9(5):125-131.

［12］何祚镛.水声作用下矩形弹性-粘弹性复板的振动和散射声近场(I)-矩形复板的振动分析［J］.声学学报，1985，10(6):344-357.

［13］何祚镛.结构振动与声辐射［M］.哈尔滨:哈尔滨工程大学出版社，2001.