基于MPI的三维瑞雷面波有限差分并行模拟

张明财，熊章强，张大洲

（1.中国水电工程顾问集团公司西北勘测设计研究院，陕西西安710043；2.中南大学地球科学与信息物理学院，湖南长沙410083）

瑞雷面波凭借其衰减小、信噪比高、抗干扰能力强、分辨率高以及在层状介质中所具有的频散特性，在地震勘探中有着广泛的应用，其正演模拟也成为国内外学者的研究热点。Hestholm［1］通过模拟对比二维、三维空间中的瑞雷面波发现，二维介质难以模拟实际的面波传播特性。董良国等［2－3］对一阶弹性波方程交错网格高阶差分解法进行了研究，给出了差分方程的稳定性条件。Igel等［4］给出了三维球坐标系下的交错网格有限差分公式，并对地震波场进行了数值模拟。Peter等［5］利用四阶有限差分交错网格对三维介质中的瑞雷面波进行了数值模拟，研究了镜像法处理自由地表时瑞雷面波的精度与最小波长内网格点数的关系。熊章强［6］通过正演模拟，对复杂介质下的瑞雷面波传播特征进行研究，利用高阶交错网格有限差分对垂直界面、斜界面、垂直低速带等复杂模型进行了正演模拟计算，并提取相应的频散曲线进行了分析。周竹生等［7］利用交错网格有限差分对弹性介质中的瑞雷面波进行正演模拟研究，在人工边界上采用了变系数吸收边界条件，避免了角点绕射，在层状介质（软弱夹层、连续介质）模型中取得了较好的应用效果；裴正林［8］给出了三维各向同性介质中一阶应力－速度弹性波方程交错网格任意偶数阶精度有限差分格式，推导出三维各向同性弹性介质完全匹配层吸收边界条件公式和相应的交错网格高阶有限差分格式。

自由地表的处理是瑞雷面波数值模拟的重要部分，许多学者经过研究提出的方法主要有如下几种：以真空形式处理应力的自由边界法［9］、应力镜像法［10］、横向各向同性介质代替自由边界法［11］和声学－弹性介质边界代替自由边界法［12］。由于声学－弹性介质边界代替自由边界法符合物理规律，易于编程实现，应用效果良好，我们利用该方法处理自由地表。

基于单PC机的串行算法势必会受到当前计算机数据存储量小、运算速度慢的限制，采用并行计算技术增加数据存储量、减少正演模拟时间是一条非常有效的途径。王月英［13］采用基于 MPI的并行算法对三维波动方程进行了有限单元正演模拟，并验证了该算法的可行性和有效性；Minkoff［14］研究了三维速度－应力有限差分地震波数值模拟方法，通过数值模拟提高了运算规模和效率；何兵寿等［15］研究了利用有限差分法并行求解该方程的基本思路与方法，极大地提高了数值求解弹性波方程的计算效率。

MPI是一种比较著名的应用于并行环境的消息传递标准，其目的是为基于消息传递的并行程序设计提供一个高效、可扩展、统一的编程环境。MPI由消息传递库函数具体实现，目前应用比较广泛 的 有 MPICH 和 LAMMPI［16］。我 们 选 用MPICH 1.2.7版本。

1 三维弹性波动方程的有限差分数值模拟算法

在三维各向同性弹性介质中，一阶速度－应力方程可以表述为［1］

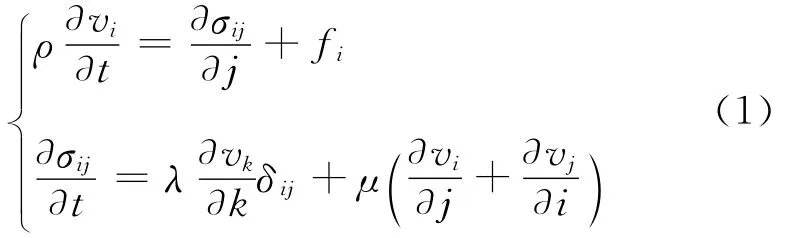
式中：i，j，k∈｛x，y，z｝；δij为 Kronecker记号；ρ表示介质密度；fi，vi分别表示体力和速度的i分量；σij表示应力分量；λ，μ为拉梅常数。

在交错网格有限差分计算中，为了保证在空间上具有偶数阶精度，将正应力 （σxx，σyy，σzz）和模型参数 （ρ， λ，μ）置于节点 （i，j，k），切 应 力σxy置于节点（i＋1／2，j＋1／2，k），切应力σxz置于节点（i＋1／2，j，k＋1／2），切应力σyz置于节点（i，j＋1／2，k＋1／2），速度分量u，v，w 分别置于 （i＋1／2，j，k），（i，j＋1／2，k），（i，j，k＋1／2），如图1所示。

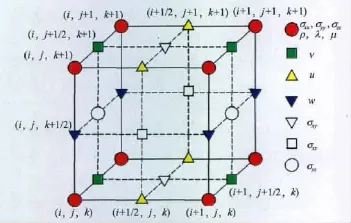
图1 交错网格中速度分量和应力分量的空间位置关系

为了使交错网格有限差分在时间上具有2 M阶精度，在t＋Δt／2时刻计算速度分量u，v，w，而在t时刻计算应力分量σxx，σxy，σxz，σyy，σyz和σzz。一阶速度－应力弹性波动方程（1）可用交错网格有限差分求解。f（x，t）对于时间的导数∂f（x，t）／∂t可用中心差分表示，对于空间的导数∂f（x，t）／∂x可用向前、向后差分表示，即［2－3］

其中，Δt表示时间步长，Δh表示空间离散网格大小。（2）式即为时间域求导的有限差分离散格式，（3）式和（4）式为空间域求导的有限差分离散格式。将（2）式至（4）式代入一阶速度 －应力方程（1）中，即可求解出弹性波动方程。

2 自由边界条件

在有限差分计算中，自由边界条件直接影响着瑞雷面波数值模拟的正确性。表1罗列了几种处理自由地表边界条件的方法在三维情况下的具体实施过程。我们选用声学－弹性介质边界代替自由边界法，在三维介质中将自由边界网格点的介质参数按表1进行特殊处理，自由边界以下网格点的介质参数不变，速度分量和应力分量按照正常的有限差分离散格式进行计算。

表1 自由地表处理方法

3 并行设计

利用交错网格有限差分进行瑞雷面波数值模拟的特点如下：①在时间域中，速度分量（n＋1）／2时刻的波场值由其（n－1）／2时刻的波场值和应力分量n时刻的波场值计算得到；应力分量n＋1时刻的波场值由其n－1时刻的波场值和速度分量（n－1）／2时刻的波场值计算得到；②在空间域中，速度和应力分量在任意网格点处的波场值只由各自周围有限个网格点上的波场值计算得到。据此可知，运算任务具有良好的局部性和并行度，可将其分解为若干个子任务，这些子任务可以并行地执行，以期达到并行求解波动方程的目的。

3.1 模型划分

设总的模型规模为N＝Nx×Ny×Nz，其中Nx，Ny，Nz分别为x，y，z方向的网格点数。将模型沿x，y，z方向分别分解为Px，Py，Pz个小区间，即可将总的模型规模分解到NP＝Px×Py×Pz个子进程中，每个子进程中的网格规模为N／NP。各个子进程均具有自己独立的内存空间，数据在整个计算空间中不重复占用内存，程序并没有因为并行运算而额外增加内存开销。

3.2 数据通信

图2 相邻进程数据通信

在空间四阶有限差分数值模拟时，每个子进程中的模型空间均需沿x，y，z方向划分出2个网格点组成过渡层。子进程在每个时间步长计算出该进程模型空间的波场值（包括应力分量和速度分量）后，必须与其相邻的进程间通过过渡层进行数据通信（发送或接收）。图2为二维情形数据通信示意图，其中，浅灰色区域表示数据发送源地址，深灰色区域表示数据接收目的地址，数据按箭头方向传递。图2中进程1的右部与进程2的左部通信，进程1的上部与进程4的下部通信，进程2的上部与进程3的下部通信，进程3的左部与进程4的右部通信。由于进程1的左部、下部，进程2的右部、下部，进程3的右部、上部及进程4的左部、上部没有相邻的进程，故不需要设置过渡层。

3.3 基于MPI的有限差分计算程序流程

基于MPI的有限差分计算程序设计流程如图3所示，具体步骤描述如下。

1）初始化MPI获取通信器及进程总数和进程序号。

2）每个子进程读取指定模型空间的模型参数，包括纵波速度vP，横波速度vS，密度ρ，主进程读取检波器坐标、震源信息。

3）主进程将震源信息、检波器坐标广播到子进程中，将各子进程中的模型参数进行归约，判断频散条件和稳定性条件。

4）时间循环开始，各个子进程判断震源坐标是否位于本进程计算区域，如果是，则读取震源函数，将震源施加于相应的位置。

5）各个子进程计算波场，并根据模型关系处理自由边界和吸收边界。以图2所示的进程为例，进程3、进程4的上边界为自由边界，进程1、进程4的左边界，进程2、进程3的右边界，进程1、进程2的下边界为吸收边界。

6）进程之间通过阻塞式标准消息发送和接受函数进行数据的交换，更新每个进程中的波场信息。

7）对各个进程中的波场信息进行归约，由主进程输出指定时刻的波场快照。

8）判断时间循环是否结束，如果没有结束，则转至步骤4）再次循环；如果结束，则调用 MPI函数MPI＿Finalize退出MPI，结束程序。

3.4 PC机多进程并行效率比较

设计一模型，大小为100m×100m×100m，网格大小dx＝dy＝dz＝1m，总的网格数为N＝1×106个，采样间隔为0.4ms，总采样时间长度为0.1s。其三维速度－应力有限差分数值模拟过程中共需存储9个三维数组（3个速度分量和6个应力分量），在单机运行时，需消耗9×N×8字节的内存，若将2台PC机组成一个PC集群，则每台PC机仅需消耗9×N×4字节的内存。在双核PC机上分别开设1，2，4，8个进程对上述模型进行有限差分数值模拟，统计出不同进程数时的串行部分计算时间WS，并行部分计算时间 WP，采用Amdnhl加速性能定律来求取加速比S：

图3 基于MPI的有限差分计算程序流程

式中：P为总进程数。表2给出了不同进程数的串行、并行CPU时间及加速比，其中进程数为1表示只进行串行计算。由表2可知：

1）随着进程数P的增加，每个进程的网格规模会减小，为待模拟网格规模的1／P。

2）进行并行计算（即进程数大于1时）后，串行计算的时间略有增加，并行计算的时间略有减少，但总的运行时间约为只进行串行计算时的1／2，这是因为计算所用的PC机只具备2个运算核心，当进程数大于2时，每个核心运行多个进程，单核中的两个进程之间增加的通信任务会消耗CPU时间。

3）加速比S随着进程数P的增加而增加，但与进程数增加速度的差距越来越大，这是因为①进程数越多，势必会增大各进程之间的通信时间；②并行并非严格执行，某些进程中会执行一些必要的输入输出，此时其余的进程可能处于等待状态。

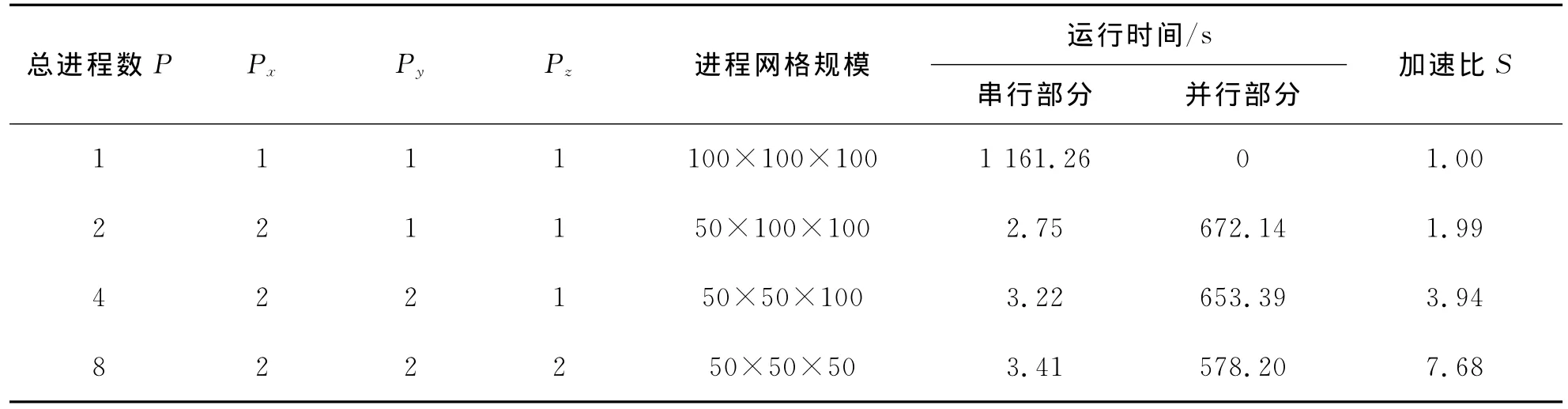
表2 不同进程数并行计算加速效率比较

4 瑞雷面波模拟算例

4.1 均匀半空间中的瑞雷面波

均匀各向同性弹性半空间介质是一种理想的模型，也是最早证明瑞雷面波存在的假设，它为研究瑞雷面波的某些传播特性提供了简单方便的方法。为了验证本文有限差分并行计算程序的正确性，设计均匀各向同性介质模型，大小为400m×400m×400m，网格间隔dx＝dy＝dz＝1m，纵波速度vP＝1 000m／s，横波速度vS＝577m／s，密度ρ＝2 100kg／m3；震源为25Hz的高斯一阶导数函数，位于坐标（200m，200m，0）处，采样间隔为0.4ms，总采样时间长度为400ms，延时40ms。在高性能计算机上申请4个节点，每个节点上申请8个CPU，共计32个CPU，每个CPU开设1个计算进程，1个进程中的网格规模为100×104个。

图4为距震源50m（150m，200m，0）和100m（100m，200m，0）处接收的地震信号与解析解对比的结果，解析解由Lamb问题解析法得到，其中的Green函数计算部分由Cagniard－de Hoop法解析得到。图4a和图4b分别表示距震源50m（150m，200m，0）处的水平和垂直方向速度分量，图4c和图4d分别表示距震源100m（100m，200m，0）处的水平和垂直方向速度分量，两处速度分量都与解析解吻合很好，说明本文有限差分并行计算程序是正确的，用声学－弹性介质近似自由地表是行之有效的。

图4 数值解与解析解对比

图5为60，160，260ms时vx，vy，vz分量的波场快照，以震源为顶点对模型区域做切割（即x＝200m，y＝200m，z＝0）处理。分析波场快照可知：瑞雷面波沿自由地表（z＝0）传播，其能量强于体波，且衰减很慢，特别是从vz分量的波场快照可以发现，沿深度方向，瑞雷面波的能量大多集中于25m以内，即一个波长之内，深度方向超过一个波长后，P波逐渐变得清晰，说明瑞雷面波的穿透深度为一个波长。

为了更加清晰地分析波场快照，选取y＝200m所在平面内的vz分量260ms时波场快照，如图6所示，震源位于（x＝200m，z＝0）处。在波场快照中可以很清楚地看到能量很强的瑞雷面波、横波和纵波。此外还可以看出，在吸收边界处没有产生强烈的反射波，说明程序中使用的吸收边界条件是有效的，达到了预期的目的。

图7为各分量的波场记录。由图7不难发现：各分量波场记录中面波的能量强于直达P波，瑞雷面波的同相轴都为直线，说明瑞雷面波在均匀各向同性介质中没有发生频散现象，这与地震勘探理论一致，也进一步证明了本文有限差分计算程序的正确性。

应用相移法提取vx分量的频散曲线，结果如图8所示。由图8可以直观地看出均匀介质中瑞雷面波的频散曲线为一条直线，说明在均匀介质中瑞雷面波不会发生频散。

4.2 水平层状速度递增模型介质中的瑞雷面波

通常情况下地层速度随着深度的增大而增大，故设计一个3层速度递增模型，如表3所示。数值模拟过程中采用25Hz的高斯一阶导数作为激发震源，模型大小为200m×200m×100m，网格间距取dx＝dy＝dz＝0.5m，模型网格为400个×400个×200个，开辟32个进程进行并行计算。

表3 速度递增模型参数

图9为水平层状速度递增模型vx，vy，vz分量的波场快照。由图9可以看出，由于各层介质的参数不同，波场快照中出现了很明显的频散，大部分能量聚集在模型表面附近。由于分层界面的存在，震源激发的SV波在界面处发生反射，此反射波以大于临界角的角度入射到自由地表会转换为P波，该P波为非均匀平面波；震源激发的P波以球面波的形式在介质中传播，该球面波可由Sommerfeld积分公式分解为很多非均匀平面波［17］，其中的非均匀SV波和由反射形成的非均匀P波叠合形成频散的瑞雷面波。随着时间的推移，在各界面处发生多次反射，形成复杂的非均匀P波和SV波，这些波相互叠合形成多种模态的瑞雷面波，其幅度随着深度的增加呈指数递减。

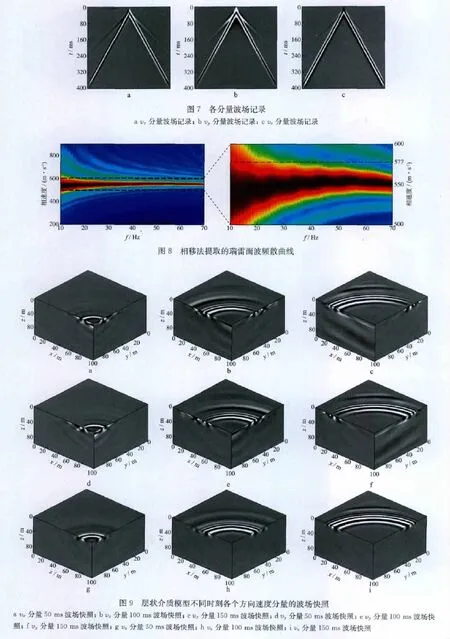
图10a为x＝100m平面上记录到的vz分量单炮波形记录。为了进一步分析频散现象，利用相移法提取vz分量波形记录频散曲线，如图10b所示。图10b中白色方块为采用快速标量传递矩阵法［18］得到的解析解，可见基阶模式和高阶模式的频散曲线都吻合得比较好。这进一步说明了瑞雷面波模拟方法的正确性。

图10 单炮波形记录及其频散曲线

5 结束语

弹性波有限差分数值模拟具有良好的并行特征，基于MPI的并行计算通过将待模拟区域划分为若干个子进程中的子区域，每个子进程相互通信完成消息传递，有效地增加了三维弹性波数值模拟的网格规模，提高了计算效率，为进一步研究三维空间中瑞雷面波的传播特性奠定了基础。

致谢：感谢中南大学高性能计算中心提供计算平台。

［1］Hestholm S O.Finite－difference seismic wave modeling including surface topography［D］.Texas：Univer－sity of Houston，1999

［2］董良国，马在田，曹景忠，等.一阶弹性波方程交错网格高阶差分解法［J］.地球物理学报，2000，43（3）：411－419 Dong L G，Ma Z T，Cao J Z，et al.A staggered－grid high－order difference method of one－order elastic wave equation ［J］.Chinese Journal Geophysics，2000，43（3）：411－419

［3］董良国，马在田，曹景忠.一阶弹性波方程交错网格高阶差分解法稳定性问题［J］.地球物理学报，2000，43（6）：856－864 Dong L G，Ma Z T，Cao J Z.A study on stability of the staggered－grid high－order difference method of first－order elastic wave equation［J］.Chinese Journal Geophysics，2000，43（6）：856－864

［4］Igel H，Nissen－Meyer T，Jahnke G.Wave propagation in 3Dspherical sections：effects of subduction zones［J］.Physics of the Earth and Planetary Interiors，2002，132（1）：219－234

［5］Peter M，Jozef K，Ladislav H.3Dfourth－order staggered－grid finite－difference schemes：stability and grid dispersion［J］.Bulletin of the Seismological Society of America，2000，90（3）：587－603

［6］熊章强.复杂介质中瑞雷面波的正演模拟及传播特征研究［D］.武汉：中国地质大学（武汉），2006 Xiong Z Q.Forward modeling and propagation characteristics research of Rayleigh wave in complex media［D］.Wuhan：China University of Geosciences（Wuhan），2006

［7］周竹生，刘喜亮，熊孝雨.弹性介质中瑞雷面波有限差分法正演模拟［J］.地球物理学报，2007，50（2）：567－573 Zhou Z S，Liu X L，Xiong X Y.Finite－difference modeling of Rayleigh surface wave in elastic media［J］.Chinese Journal Geophysics，2007，50（2）：567－573

［8］裴正林.三维各向同性介质弹性波方程交错网格高阶有限差分法模拟［J］.石油物探，2005，44（4）：308－315 Pei Z L.Numerical simulation of elastic wave equation in 3－D isotropic media with staggered－grid highorder difference method［J］.Geophysical Prospecting for Petroleum，2005，44（4）：308－315

［9］Zahradník J，Priolo E.Heterogeneous formulations of elastodynamic equations and finite－difference schemes［J］.Geophysical Journal International，1995，120：663－676

［10］Graves R W.Simulating seismic wave propagation in 3Delastic media using staggered－grid finite differences［J］.Bulletin of the Seismological Society of A－merica，1996，86（4）：1091－1106

［11］Mittet R.Free－surface boundary conditions for elastic staggered－grid modeling schemes［J］.Geophysics，2002，67（5）：1616－1623

［12］Xu Y X，Xia J H，Miller R D.Numerical investigation of implementation of air－earth boundary by a－coustic－elastic boundary approach［J］.Geophysics，2007，72（5）：147－153

［13］王月英.基于MPI的的三维波动方程有限元法并行正演模拟［J］.石油物探，2009，48（3）：221－225 Wang Y Y.3Dwave－equation finite－element forward modeling based on message passing interface parallel computing［J］.Geophysical Prospecting for Petroleum，2009，48（3）：221－225

［14］Minkoff S E.Spatial parallelism of a 3Dfinite difference velocity－stress elastic wave propagation code［J］.SIAM Journal on Scientific Computing，2002，24（1）：1－19

［15］何兵寿，张会星，韩令贺.弹性波方程正演的粗粒度并行算法［J］.地球物理学进展，2010，25（2）：650－656 He B S，Zhang H X，Han L H.Forward modeling of elastic wave equation with coarse－grained parallel algorithm［J］.Progress in Geophysics，2010，25（2）：650－656

［16］张林波，迟学斌，莫则尧，等.并行计算导论［M］.北京：清华大学出版社，2006：175－182 Zhang L B，Chi X B，Mo Z Y，et al.Introduction to parallel computing［M］.Beijing：Tsinghua University Press，2006：175－182

［17］巴特.地震学的数学问题［M］.郑治真，译.北京：科学出版社，1976：229－234 Bart M.Mathematical problem of seismology［M］.Zhen Z Z，translator.Beijing：Science Press，1976：229－234

［18］凡友华，肖柏勋，刘家琦.计算层状介质中轴对称柱面瑞雷面波频散函数的δ矩阵法［J］.物探与化探，2001，25（2）：109－116 Fan Y Y，Xiao B X，Liu J Q.Theδmatrix method for the dispersion function computation of axis symmetrical cylindrical Rayleigh wave in multilayered media［J］.Geophysics ＆ Geochemical Exploration，2001，25（2）：109－116