如何用SAS软件正确分析生物医学科研资料XXV.结果变量为多值名义变量的高维列联表资料的统计分析与SAS软件实现（一）

王琪，胡良平

针对高维列联表（表中涉及到的定性变量的个数 k ≥3）资料的分析，前四期的讲座分别介绍了结果变量为二值变量的高维列联表和结果变量为多值有序变量的高维列联表资料的统计分析与SAS 软件实现，本文将详细介绍结果变量为多值名义变量的高维列联表资料及其用 SAS 软件实现统计分析的内容。

分析结果变量为多值名义变量的高维列联表资料时，可以选用的统计分析方法有CMH χ2检验、对数线性模型和扩展的多重 logistic 回归分析，本文重点介绍前两种方法。

1 CMH χ2 检验[1]

在高维列联表中，当结果变量为多值名义变量时，选用一般关联统计量，也就是 FREQ过程 CMH 检验输出结果中的第三项，其自由度 ν=(R-1) (C-1)。它的具体计算公式可以参见本刊 2013年第 3 期，在计算该统计量时，行的评分阵 Rh与计算行平均得分统计量的行评分矩阵相同，即Rh=[IR－1,–JR－1]；列的评分阵 Ch可以被类似地定义为：

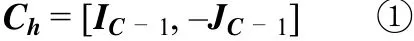
其中 IC－1是秩为C－1的单位阵，JC－1是元素均为1的(C－1)×1的列向量。在一般关联统计量中，行的评分阵 Rh与列的评分阵 Ch都是由 FREQ 过程内部产生的。

一般关联统计量不要求原因变量或结果变量是有序的。无论原因变量是多值有序变量还是名义变量，只要结果变量是多值名义的，都可以采用该统计量。与之相对应的原假设和备择假设分别为：

H0：每层中原因变量和结果变量之间不存在关联；

H1：至少有一层，原因变量和结果变量之间存在某种关联。

当仅有一层时，该 CMH 统计量与Pearson χ2统计量的关系为：

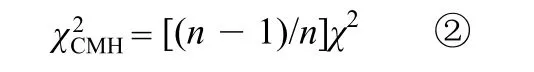
其中 n 为总例数；当有多层时，该统计量为层修正的Pearson χ2统计量。当然，相似的校正也能够通过对各层Pearson χ2统计量求和而得到，但是这种校正方法需要每层的样本含量都要足够大，而 CMH 统计量仅仅需要总的样本含量比较大。

需要说明的是，当各层的各比较组间的趋势方向一致时，CMH 方法比较有效；当各层的各比较组间的趋势方向不一致时，CMH 方法则不容易检出差别，此时应单独考察各层或采用其他方法。

2 对数线性模型

结果变量为多值名义变量的高维列联表资料同样也可以采用对数线性模型进行分析，其基本的原理与分析结果变量为二值变量的高维列联表资料基本相同[2]，详见本刊 2013年第 2 期，本文仅结合实例向读者介绍如何通过SAS 软件使用 CMH χ2检验和对数线性模型处理结果变量为多值名义变量的高维列联表资料。对软件实现和结果解释作进一步说明。

【例1】调查某中医院一日内医生开出的针对甲、乙两种疾病的处方情况，结果见表1，试对数据进行分析。

表1 不同疾病、不同性别患者的药物使用情况

分析与解答：此表中含有三个定性变量，分别为疾病类型、患者性别、药物种类，结果变量为药物种类（多值名义变量），数据以列联表的形式呈现，因此该表被称作“结果变量为多值名义变量的三维列联表”。对于该高维列联表资料，分析目的是考察不同疾病、不同性别的患者所用药物种类频数构成有无差别，分析时通常可选用 CMH χ2检验、对数线性模型或扩展的多重 logistic 回归分析。本期重点介绍前两种。

⑴ CMH χ2检验：CMH χ2检验可以控制外侧影响相对次要的变量而得到最内侧两个变量之间的关系。如果我们想控制住性别的影响，分析疾病类型与药物种类之间的关系，此时可以使用 CMH χ2检验。SAS 程序如下，设程序名为li1.sas。

data a1; /*1*/do a=1 to 2;do b=1 to 2;do c=1 to 3;input f @@;output;end; end; end;cards;52 7 234 8 123 19 418 11 3;run;ods html;proc freq data=a1; /*2*/tables b*a*c/cmh;weight f;run;ods html close;

程序说明：本例第一步建立数据集 a1，a 表示疾病类型，a=1 表示甲，a=2 表示乙；b 表示患者性别，b=1 表示男性，b=2 表示女性；c 表示药物种类，c=1 表示中药，c=2 表示西药，c=3 表示复方药；变量 f 表示频数。多值名义资料的CMH 检验仍然采用 FREQ 过程，在tables语句中依次列出性别、疾病类型和药物种类，列在第一位的变量是需要控制的原因变量，列在第二位的变量是想要考察的原因变量，列在第三位的变量是结果变量。Tables 语句中的选项 cmh 指定输出CMH 统计量。ods html 语句则要求以 HTML（网页）格式输出结果。

SAS 程序运行结果：首先输出的是两个二维列联表（略），这是按性别分层以后，疾病类型和药物种类所形成的2×3 列联表，其中包括频数、百分比、行百分比和列百分比。

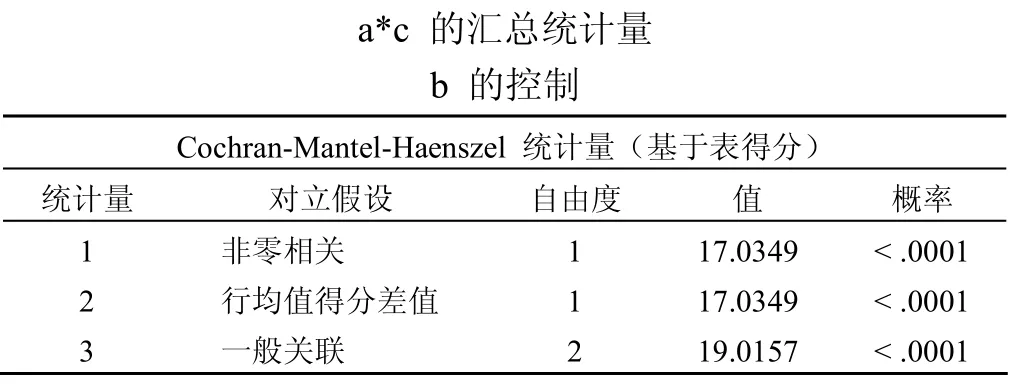
FREQ 过程

输出结果的第二部分是三个 CMH 统计量，这些统计量都是在使用 table 方法打分的基础上计算的。本例中结果变量是多值名义的，因此无论原因变量是二值的、多值有序的或多值名义的，都应该使用一般关联统计量。此处自由度ν=2=19.0157，P＜0.0001。总的样本含量为182 例。

统计学与专业结论：本例CMH 检验中的P＜0.05，拒绝原假设 H0，接受 H1，说明在控制了性别因素的基础上，疾病类型与药物种类之间存在一定的关联。结合列联表中的行百分数可以看到，相对来说，甲病患者中使用中药的人数比例要大于乙病患者，也就是说甲病患者的中药使用率比乙病患者高。

⑵对数线性模型：若想要考察疾病类型、性别和药物种类三者之间的关系，可以考虑采用对数线性模型。SAS 程序如下，设程序名为li2.sas。

data a2; /*1*/do a=1 to 2;do b=1 to 2;do c=1 to 3;input f @@;output;end; end; end;cards;52 7 234 8 123 19 418 11 3;run;ods html;proc catmod data=a2; /*2*/weight f;model a*b*c=_response_;loglin a|b|c;run;proc catmod data=a2; /*3*/weight f;model a*b*c=_response_;loglin a|b|c @2;run;proc catmod data=a2; /*4*/weight f;model a*b*c=_response_;loglin a b c a*c;run;ods html close;

程序说明：本例第一步建立数据集 a2，同 li1.sas。然后第二步调用 catmod 过程，采用饱和模型进行对数线性模型分析，“model a*b*c=_response_;”语句中等号左端的a*b*c 指明要分析的变量，等号右端的_response_ 表示拟合对数线性模型；“loglin a|b|c;”语句中的a|b|c 表示拟合所有的主效应与交互效应，即饱和模型，该语句等同于“loglin a b c a*b a*c b*c a*b*c”。第三步调用 catmod 过程，采用一阶交互效应模型进行对数线性模型分析，该模型包括主效应和所有的一阶交互效应（即在饱和模型中去掉最后一项，它是二阶交互效应项），“loglin a|b|c @2;”语句表示拟合一阶交互效应模型。第四步调用 catmod 过程，拟合最优模型，语句“loglin a b c a*c;”中包含了主效应和a*c 一阶交互效应。

SAS 程序运行结果：

⑴饱和模型：

Maximum likelihood analysis of variance

以上是方差分析表，使用最大似然法进行分析。这里三个因素之间的二阶交互作用 a*b*c 经检验没有统计学意义（P ＞0.05），一阶交互作用中仅 a*c 有统计学意义（P＜0.05）。由于这里建立的是饱和模型，已经没有剩余的自由度分配给似然比检验，所以并没有关于模型拟合情况的似然比检验的结果。

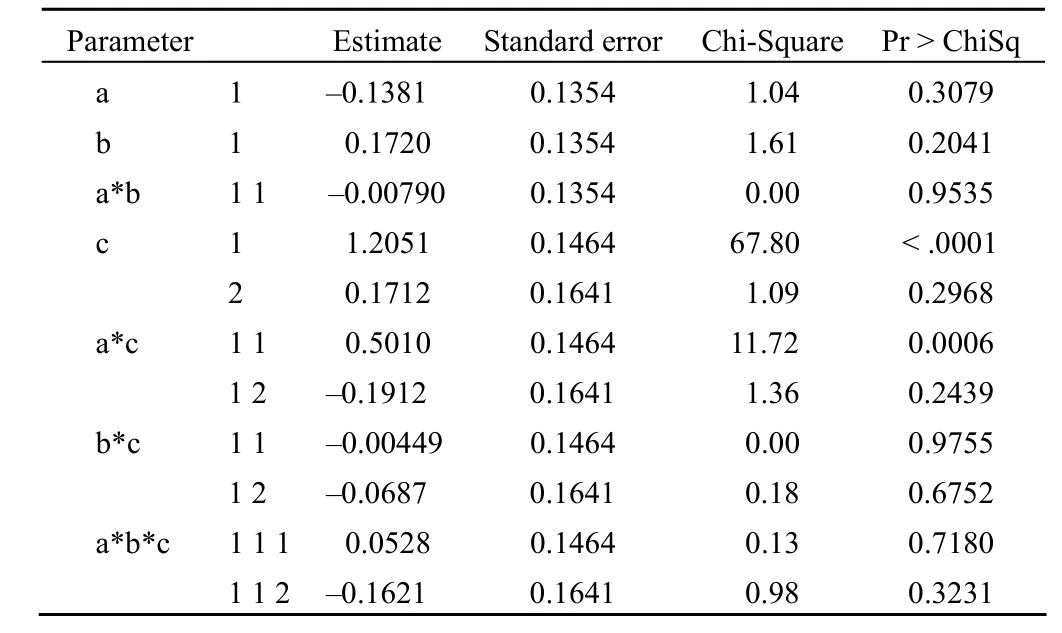
Analysis of maximum likelihood estimates

上表给出了模型中参数的估计值以及对其进行假设检验的结果。这部分结果与方差分析表的结果一致。参数估计值默认将每个效应的最后一类作为参照类，其他各个水平通过与参照类相比来分析效应大小。如疾病类型与药物种类的交互效应（a*c）在两个变量取值都为1 时的参数估计值为0.5010（P=0.0006），与0的差别有统计学意义，表示甲病组（a=1）与乙病组（a=2）相比，使用中药的倾向性存在差别，甲病患者比乙病患者更倾向于使用中药。由于饱和模型无法进行假设检验，且二阶交互效应项也无统计学意义，可以考虑首先将此项从模型中删除，以简化模型。

⑵一阶交互效应模型：

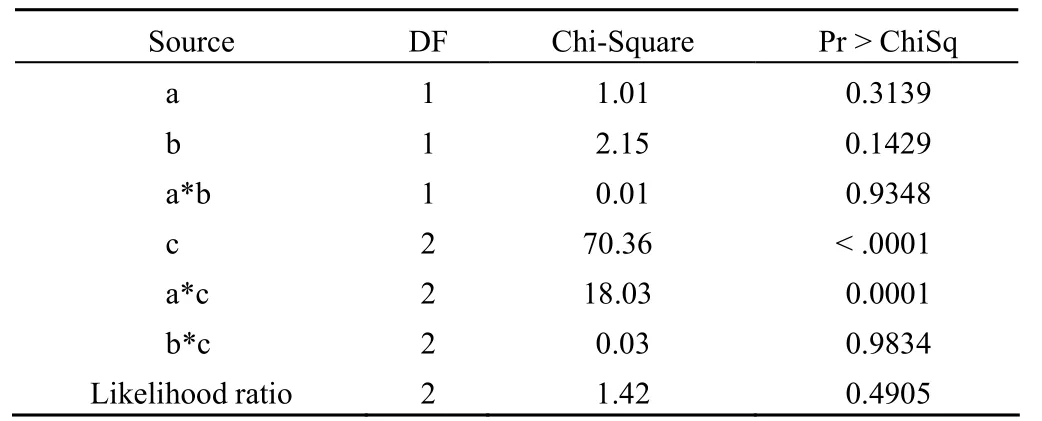
Maximum likelihood analysis of variance

一阶交互效应模型仅列出方差分析表，结果提示，疾病类型是患者所用药物种类的影响因素。似然比检验的结果为χ2=1.42，P=0.4905（此结果表明该模型对资料的拟合效果较好）。考虑到模型中还包含有无统计学意义的项，需要进一步优化。

⑶最优模型的筛选：

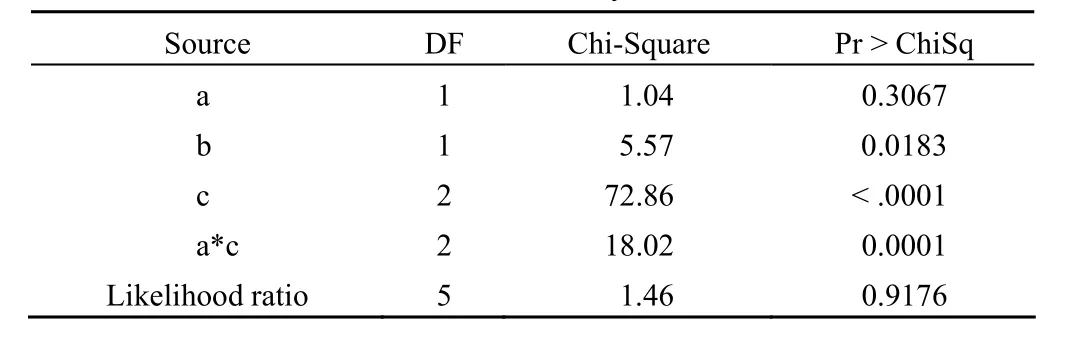
Maximum likelihood analysis of variance

由于在一阶交互效应模型拟合过程中，a*b 项和b*c项无统计学意义，我们将其剔除出模型。最终的模型包括的一阶交互作用仅有 a*c，方差分析的结果表明在新模型中a*c 项的作用仍然是有统计学意义的。似然比检验的结果χ2=1.46，P=0.9176 ＞0.05，说明模型对资料的拟合效果非常好，可以认为该模型不仅成立而且已达到最优程度。尽管因素 a的假设检验结果无统计学意义，但由于对数线性模型是嵌套式结构，只要模型中有高阶项，所有比它低阶的项都必须保留在模型中。

Analysis of maximum likelihood estimates

在参数估计的结果中，疾病类型和患者性别有两个水平，自由度均为1，所以参数估计部分对应一行结果；而药物种类有三个水平，自由度为2，因此参数估计的结果有两行，分别代表中药相对于复方药、西药相对于复方药对相应网格中理论频数的对数值的影响情况[前者差别有统计学意义（P＜0.0001）、后者差别无统计学意义（P=0.2922）]；疾病类型和药物种类两个因素交互作用项的参数估计结果也有两行，其结果解释参见下面的专业结论部分。

专业结论：由于疾病类型和药物种类的交互作用项有统计学意义，同时结合实际资料可知，在甲病和乙病患者中，三种药物使用的构成比不同，在甲病患者中，使用中药所占的比例要明显高于乙病患者；而在乙病患者中，使用中药和使用西药的比例没有明显的区别。

[1]Hu LP.Medical statistics-analysis of quantitative and qualitative data applying the triple-type theory.Beijing: People’s Military Medical Press, 2009:376-393.(in Chinese)胡良平.医学统计学-运用三型理论分析定量与定性资料.北京:人民军医出版社, 2009:376-393.

[2]Hu LP.Statistics facing practical scientific issues -- (2) multi-factor designs and linear model analysis.Beijing: People’s Medical Publishing House, 2012:547-566.(in Chinese)胡良平.面向问题的统计学——(2)多因素设计与线性模型分析.北京:人民卫生出版社, 2012:547-566.