基于比例积分控制器的恒定相移低通滤波电路

王 帅，刘文怡，王红亮，符多铎

（1.中北大学电子测试技术国家重点实验室，山西 太原 030051；2.中北大学仪器科学与动态测试教育部重点实验室，山西 太原 030051）

0 引言

在设计电路时，低通滤波器是非常重要的模块，主要作用是从多种频率成分的复杂信号中，将感兴趣的信号提取出来。然而滤波器在滤波的同时会使输入信号产生相位偏移，而这种相移（除部分FIR数字滤波器）是非线性的［1］。滤波器应用在表面粗糙度测量时，由于2RC滤波器本身的非线性相移特性，用2RC滤波法建立的评定中线会造成表面粗糙度轮廓的严重失真［2］，此外，在相参雷达体系［3－4］和医疗成像［5］等领域也有消极影响。目前，解决问题的主要方法是通过全通滤波器［6－7］，最优 Hankel范数算法滤波器［8］或者利用时间反转法构造的零相位滤波器［9］把非线性相位偏移转换为线性相移或恒定相移，但利用全通滤波器实现线性相位偏移的条件苛刻，计算复杂，而且误差较大。零相位滤波器只能通过软件（或者虚拟仪器）实现，无法应用于实际的硬件电路［9］，因为该算法将输入信号及其时间反转后的信号相加，也就是将未来的信号序列和现在的相加，在实际电路中无法实现。为此，本文提出基于比例积分控制器的恒定相移低通滤波电路。

1 低通滤波器与比例积分控制器

1.1 低通滤波器的相位响应

一阶低通滤波器的硬件电路如图1所示［10］，传递函数表达式为：

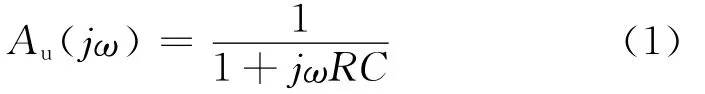
相位响应为：

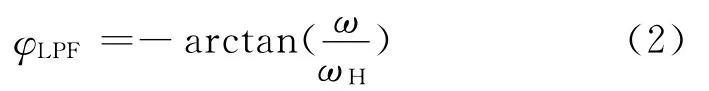
式（2）中截止频率wH＝RC。

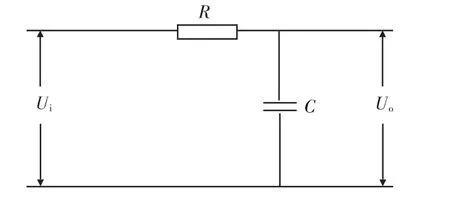
图1 一阶低通滤波器的电路图Fig.1 Circuit diagram of first－order low－pass filter

1.2 比例积分控制器的相位响应

比例积分控制器是一种线性控制，结构如图2所示，其表达式为：

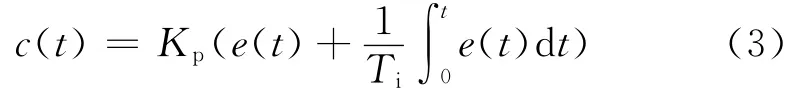
式（3）中Kp为比例积分控制器的比例系数，调节Ti影响积分控制作用，e（t）系统理想输出量r（t）和实际输出量c（t）之间的误差。

比例积分控制的传递函数的在频域表达式为：

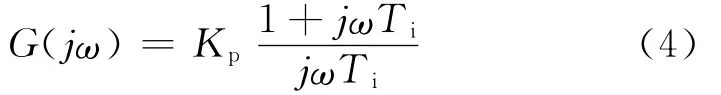
相位响应为：

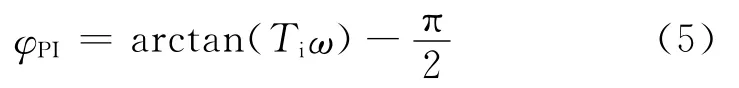
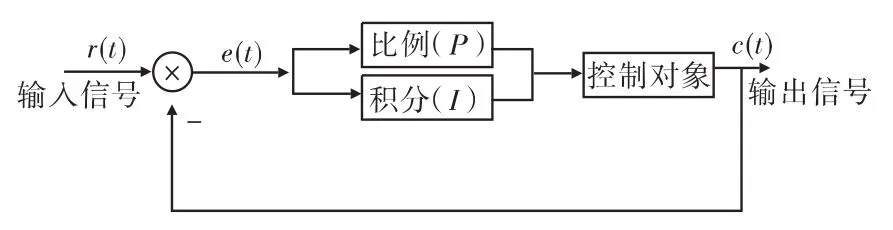
图2 比例积分控制器的结构图Fig.2 Structure of PI controller

比例积分控制是控制工程中一种技术成熟、理论完善和应用较为广泛的控制策略，通过比例控制作用调节积分作用所导致相角滞后对系统的稳定性所带来的不利影响，通过引入积分控制作用以改善系统的稳态性能［11］。

2 基于比例积分控制器的恒定相移低通滤波电路

基于比例积分控制器的恒定相移低通滤波电路的结构如图3所示，包括两个模块：N阶低通滤波器与N个比例积分控制器。该电路工作过程是：首先，设置低通滤波器的极点值Wn等于比例积分控制器积分时间常数Tin的倒数，即Tin＝1／Wn（其中W1是滤波器截止频率，n＝1，2，…，N），且低通滤波器的阶数与比例积分控制器的个数相同。然后，当信号经过N阶低通滤波器滤除噪声时，其本身产生相位偏移，而经过N个比例积分控制器同样产生偏移，但信号两次偏移的和为恒定值。最后，根据滤波器的阶数和比例积分控制器的个数，可以准确预知信号的相位偏移。

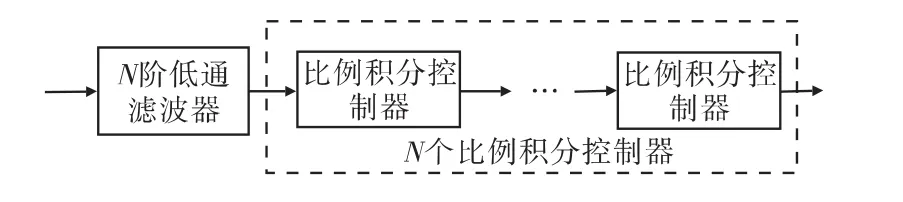
图3 恒定相移电路的结构框图Fig.3 Structure of constant phase shift system

3 验证

3.1 理论证明

如图4所示，一阶低通滤波器和一个比例积分控制器级联得到系统的相位响应为：

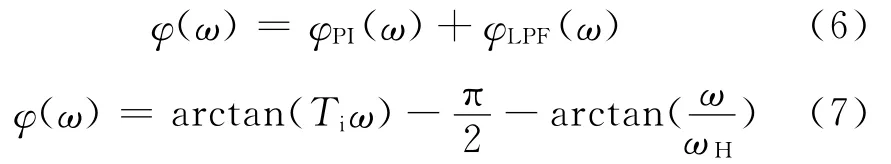
式（7）中Ti若取值Ti＝1／wH得到：

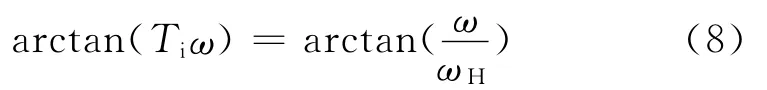
将式（8）带入式（6）的结果为：

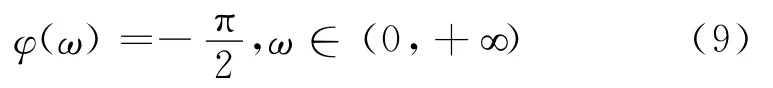
式（9）得到系统相移在整个W 中恒等于－π／2。

从前面的推理可以得出结论：当Ti＝1／wH时，一阶低通滤波器和一个比例积分控制器级联得到系统的相移值在整个频域等于－π／2。

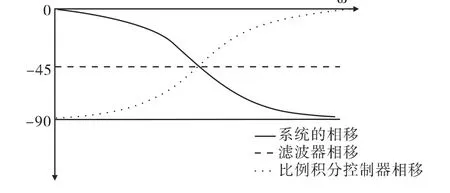
图4 一阶低通滤波器、比例积分控制器和系统相移的示意图Fig.4 Phase shift diagram of first－order low－pass filter，PI controller and the system

从这个特例推广到N阶系统：在N阶系统中，如果低通滤波器的阶数和比例积分控制器模块的个数相等，且满足低通滤波器的极点值等于比例积分控制器积分时间常数的倒数，是否可以得到在整个频域具有恒定相移？

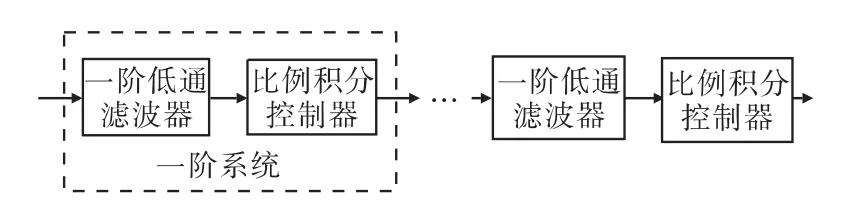
图5 N个一阶系统级联的N阶系统Fig.5 N－order system of N＊first－order systems cascaded

实现上述假设，需要分两步进行证明：

第一步：证明图5中由N个一阶系统级联组成的N 阶系统相移为恒定值，且相移值为－N·π／2。

第二步：证明图5的N阶系统与图3中由N阶滤波器和N个比例积分控制器级联的N阶系统等价。

第一步的证明：

假定n＝N时，系统的相位偏移恒定且值为－N·π／2，当n＝N＋1时，整个系统的相位偏移为：

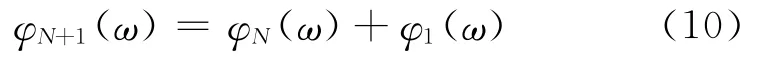
式（10）中φN（ω）为N 阶系统的相移，φ1（ω）为一阶系统的相移，且都为常数；

则φN＋1（ω）＝A ，A 为常数

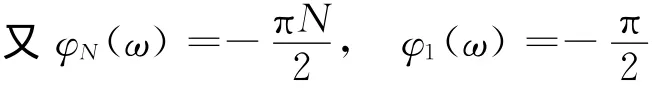
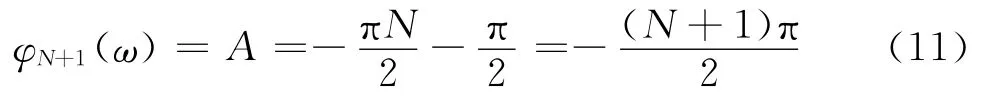
所以，当n＝N＋1时，系统的相移为常数且值为－（N＋1）·π／2，因此，图5中由N 个一阶系统级联组成的N阶系统相位偏移为恒定值，且偏移值为－N·π／2。

第二步的证明：

设低通滤波器、比例积分控制器和构成的系统在频域为Au（jw），G（jw），Y（jw），则系统在频域的表达式：

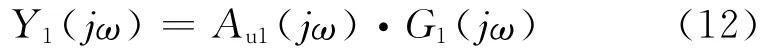
图5的N 阶系统表达式为：Yn（jω）＝Au1（jω）

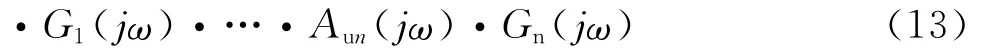
根据乘法的交换律得：

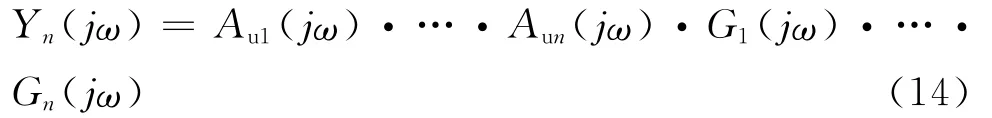
而N阶低通滤波器可以由N 个一阶低通滤波器的形式相乘构成：

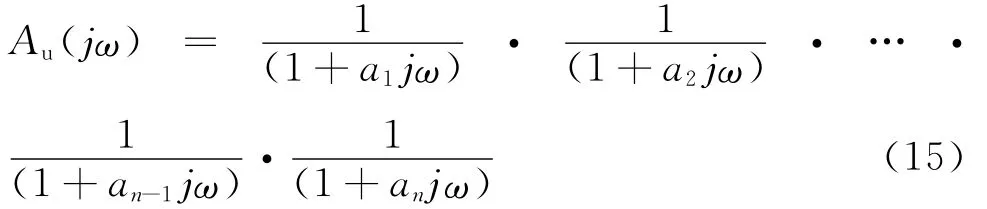
式（15）中a1，a2，…an－1，an为实数。

而式（15）可以表示为：

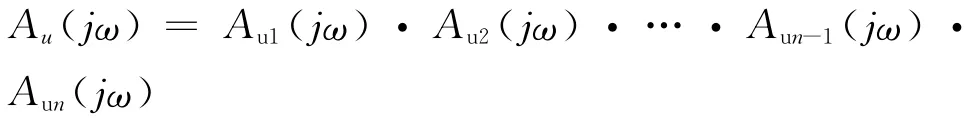
所以，图5和图3的N阶系统等价。

图5的N阶系统的相移恒定，相移值等于一阶系统的N倍且值为－N·π／2，因此，图3的N阶系统也是相移恒定，系统的相移值是－N·π／2，其中当系统阶数为4n时，通过系统的信号延迟相位为－2πn，经过处理后最终可以使周期信号经过系统时的相移为零。注意：N个比例积分控制器可以互不相同，即各个比例积分模块的参数可以互不一样，但需满足低通滤波器极点值与比例积分控制器的积分时间常数Ti的关系为Tin＝1／Wn（W1是截止频率，n＝1，2，…，N）。

3.2 仿真

为验证前面的论述，利用MALAB软件对一阶系统和四阶系统仿真分析，以此证明该电路的可行性。取一阶低通滤波器的截止频率wH＝1 000rad／s，一个比例积分控制器的Kp＝0.1，Ti＝0.001。

通过仿真对比可以得出：图6的一阶低通滤波器和图7的一个比例积分控制器的相位响应的曲线互为镜像，图8中系统相移的值在频率W∈（0，＋∞）为－π／2，由于计算存在四舍五入，误差在0.1°～0.2°。运用一阶低通滤波器和一个比例积分控制器级联的系统达到理论计算的值。

N阶系统的仿真取N＝4验证理论的一般适用性。一方面，四阶系统结构不太复杂，需要计算的值较少，误差相对就小；另一方面，四阶系统的相移为－2π，对于周期信号可以实现零相移。取四阶低通滤波器的截止频率wH（或者W1）＝1 000rad／s，其他 极 点 的 值 为 W2＝ 10 000rad／s，W3＝100 000rad／s，W4＝1 000 000rad／s，所以，相对应的四个比例积分控制器的积分时间常数为Ti1＝0.001，Ti2＝0.000 1，Ti3＝ 0.000 01，Ti4＝0.000 001，Kp1＝Kp2＝Kp3＝Kp4＝0.1。这样取值的目的是减小误差，方便观察。

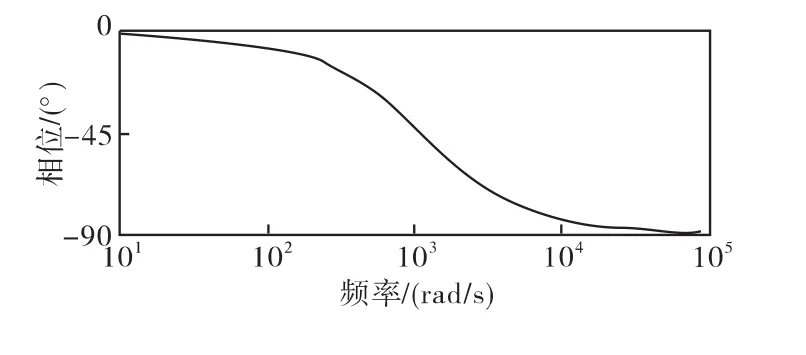
图6 一阶低通滤波器的相位响应Fig.6 Phase response of first－order low－pass filter

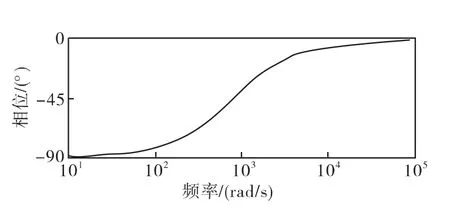
图7 一个比例积分控制器的相位响应Fig.7 Phase response of PI controller

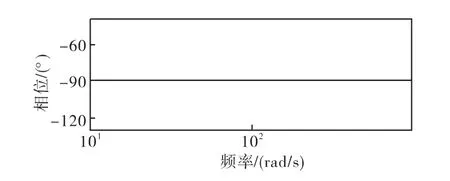
图8 一阶系统的相位响应Fig.8 Phase response of first－order system

四阶低通滤波器和四个比例积分控制器级联的相位响应如图9和图10，图11为四阶系统的相位响应，得到的相移值在W∈（0，＋ ∞）为－2π，所以利用四阶低通滤波器和四个比例积分控制器级联得到的系统达到理论计算的值。

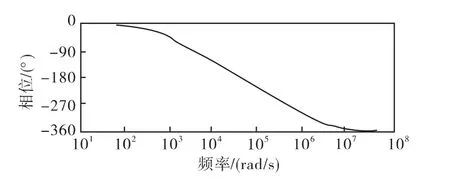
图9 四阶低通滤波器的相位响应Fig.9 Phase response of four－order low－pass filer

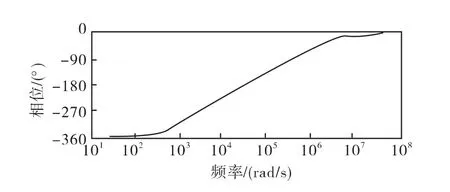
图10 四个比例积分控制器的相位响应Fig.10 Phase fesponse of four PI controllers

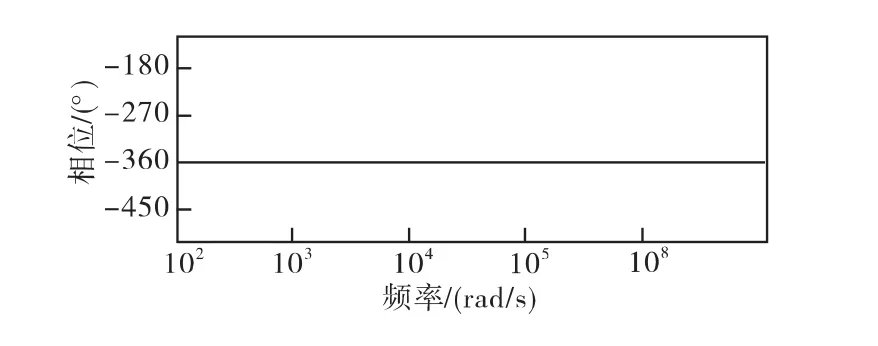
图11 四阶系统的相位响应Fig.11 Phase response of four－order system

4 结论

本文提出了基于比例积分控制器的恒定相移低通滤波电路。该电路利用低通滤波器与比例积分控制器级联，设置低通滤波器的极点值等于比例积分控制器积分时间常数的倒数，且低通滤波器的阶数与比例积分控制器的个数相同，从而使信号经过滤波器与比例积分控制器的相位偏移的和为恒定值。理论分析与仿真表明，与全通滤波器和零相移滤波器实现线性相移或恒定相移相比，本文提出的电路计算简单，误差较小，并且容易实现。

［1］曾学刚.有源滤波器的非线性交调失真［J］.电子学报，1996，1（1）：116－118.ZENG Xuegang.Nonlinear intermodulation distortion in active filter［J］.Acta Electronica Sinica，1996，1（1）：116－118.

［2］许景波，袁怡宝，朴伟英，等.表面粗糙度测量中的高斯滤波快速算法［J］.计量学报.2005，26（4）：309－312.XU Jingbo，YUAN Yibao，PIAO Weiying，et al.A fast gaussian filtering algorithm for surface roughness measurements［J］.Acta Metrlogic Sinica，2005，26（4）：309－312.

［3］Howard S D，Calder bank A R.A simple signal processing architecture for instantaneous radar polarimetry［J］.IEEE Trans.on information Theory，2007，53（4）：1282－1289.

［4］Mao X P，Liu Y T.Null phase－shift polarization filtering for high－frequency radar［J］.IEEE Trans.on Aerospace Electronic System，2007，3（4）：1397－1407.

［5］Simson MB.Use of signals in the terminal QRS complex to identify patients with ventricular tachycardia after myocardia infraction［J］.Circulation，1981，64：235.

［6］王学伟，高朝，张旭明.高准确度、宽频带90°数字相移网络的设计［J］.电测与仪表.2004，41（467）：36－38.WANG Xuewei，GAO Chao，ZHANG Xuming.The design of presicion 90digital phase－shift network in wide frequence scope［J］.Electrical Measurement ＆ Instrumentation.2004，41（467）：36－38.

［7］沈玮彬，赵艳明.相位矫正滤波器设计［J］.中国科技信息，2010，19（41）：98－102.SHEN Weibin，ZHAO Yanming.The design of rectification phase Filter［J］.China Since And Technology Information，2010，19（41）：98－102.

［8］邓娜，邵世煌，顾国祥.基于最优Hankel范数近似的线性相位IIR滤波器设计［J］.控制理论与应用.2007，24（2）：200－204.DENG Na，SHAO Shihuang，GU Guoxiang.Design of linear phase IIR filters via optimal Hankel－norm［J］.Control Theory ＆ Application，2007，24（2）：200－204.

［9］纪跃波，秦树人，汤宝平.零相位数字滤波器［J］.重庆大学学报（自然科学版），2000，23（6）：4－7.JI Yuebo，QIN Shuren，TANG Baoping.Digital filtering with zero phase error［J］.JournaI Of Chongging University（NaturaI Science Edition），2000，23（6）：4－7.

［10］华成英，童诗白.模拟电子技术［M］.北京：高等教育出版社，2006.

［11］胡寿松.自动控制原理［M］.北京：科学出版社.2007.