基于灰色系统理论的引信储存可靠性预测模型

赵 铮，刘丽群

（1.总装备部驻锦州地区军代室，辽宁 锦州 121017；2.解放军第二〇五医院，辽宁 锦州 121000）

0 引言

引信的可靠性直接决定了弹药系统的可靠性［1］。由于弹药在战时消耗量极大，因此在和平时期要有足够的储备。一般要求引信在储存15～20年后各项性能仍应满足要求［2］。但引信在储存过程中会受到来自周围环境各种激励的影响，从而引起引信的性能参数变化，导致引信系统的可靠性随储存时间的推移而发生变化［3］。如何准确预测引信在储存一定年限后的可靠性，对于装备发挥效能至关重要。

可用于求解预测模型的算法有很多，包括移动平均预测法、指数平滑法、自适应指数平滑法、一元线性回归预测法、二元线性回归预测法、BP神经网络法等。但这些方法应用在引信储存可靠性预测中，存在适用范围小、计算较为复杂、预测精度差、需大量数据训练等不足。为使预测可以适用于各种类型引信，且应用便捷、精度较高，本文将灰色系统理论引入储存可靠性预测。

1 灰色系统理论模型建模原理

按时间顺序排列的一组有序数据称为时间序列，它展示了事物在一定时间内的发展变化过程。基于数据的时间性，可以将时间序列中的每一个数据视为影响该事物发展变化众多因素综合作用的体现。据此，可对事物的规律进行预测。它符合预测的连贯原则和类推原则，即直接简便，又符合科学性［4］。

随着信息科学的发展，用于时间序列预测的算法也在发展。我国著名学者邓聚龙教授于1982年提出了灰色系统理论（简称灰理论，Grey Theory），至今已初步形成了以灰色关联空间为基础的分析体系，以灰色模型为主体的模型体系。

以灰色过程及其生成空间为基础与内涵的方法体系，以系统分析、建模、预测、决策、控制和评估为纲的技术体系，是一种适合残缺信息系统建模的理论方法。灰色系统对数据的处置不是找概率分布，求其统计规律，而是通过对原始数据的整理来寻求其变化规律［5］。这是一种就数据寻找数据的现实规律的途径，称之为灰色序列生成。灰色系统理论认为，尽管客观系统表象复杂，数据凌乱，但它总是有整体功能的，因此必然蕴含某种内在规律，关键在如何选择适当的方式去挖掘和利用它，一切灰色序列都能通过某种生成弱化其随机性，显现其规律性［6］。

灰色系统理论模型建模机理为：对于含有误差影响、呈离散状态的原始数据，先对其作累加或累减处理，淡化随机性误差影响，再以微分方程进行建模，使所建立的模型具有较高的精度，通过对模型值的还原，求得预测值。

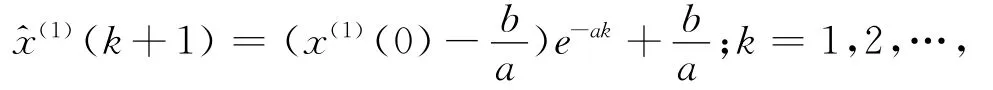
该模型具有以下特点：所需要的已知信息较少，一般只需4个以上的数据就可建立预测模型；不必知道原始数据分布的特征，对于无规律的任意光滑、离散的原始序列，通过做有限次的生成，均可转化成有规律的序列。

2 灰色系统理论预测模型

我国现阶段引信生产企业实际生产情况为：每个年度的生产任务一般包括多种型号引信，基本不存在某一型号引信连续多个批次集中生产的情况。由于同型号不同批次产品生产时机不同，气候条件、所用原材料批次、操作工人、加工设备、质量管理状况均可能有所差异，这就导致同型号不同批次的引信质量状况不尽相同，从而无法按产品型号得出所有批次产品的质量状况。引信产品这种特性，即由于多种不确定因素导致的产品质量状况，恰好可以理解为一个具有多个输入的灰系统，尽管无法通过输入直接得出产品质量状况，但其内在规律是可以通过对统计数据的加工、挖掘得到的。这完全符合灰色系统理论以部分信息已知，部分信息未知的“小样本”、“贫信息”不确定性系统为研究对象，通过对“部分”已知信息的生成、开发，提取有价值的信息，实现对系统运行行为、演化规律的正确描述的特点。

灰色预测模型GM（1，1）推导如下：

设X（0）为1～n年的引信储存可靠性实测值，

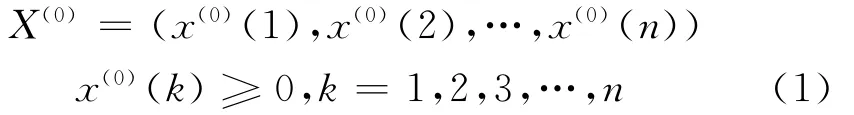
称X（1）为X（0）的1－AGO序列，表示如下：

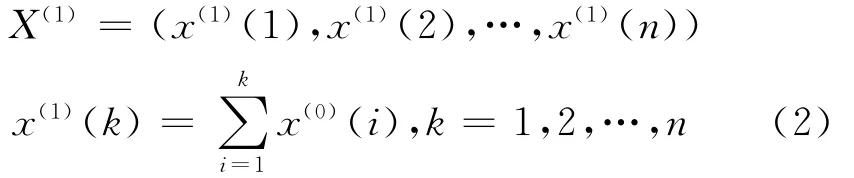
Z（1）为X（1）的紧邻均值生成序列，表示如下：

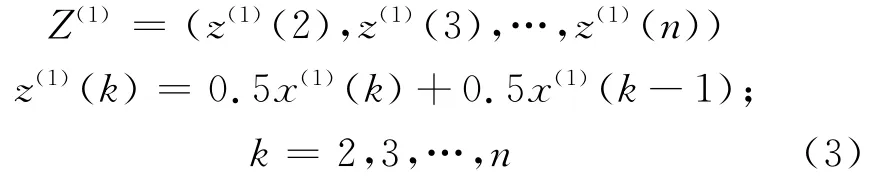
则灰 色 微 分 方 程 x（0）（k）＋az（1）（k）＝b 为GM（1，1）模型。若＝ （a，b）T为参数列，且

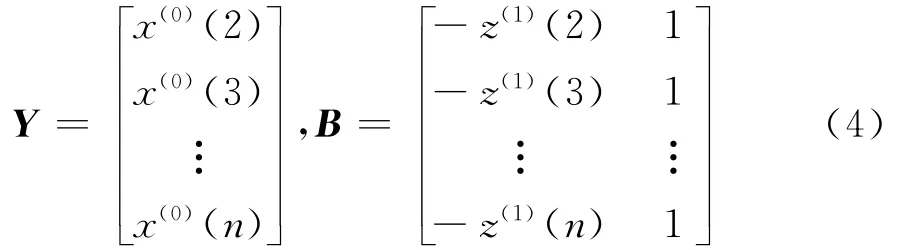
则灰色微分方程x（0）（k）＋az（1）（k）＝b的最小二乘估计参数列满足：＝ （a，b）T＝ （BTB）－1BTY，GM（1，1）灰色微分方程x（0）（k）＋az（1）（k）＝b的时间响应序列为：

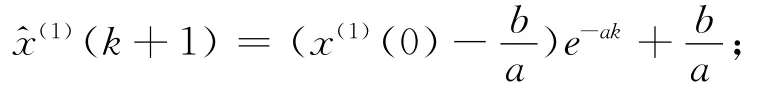
取x（1）（0）＝x（0）（1），则

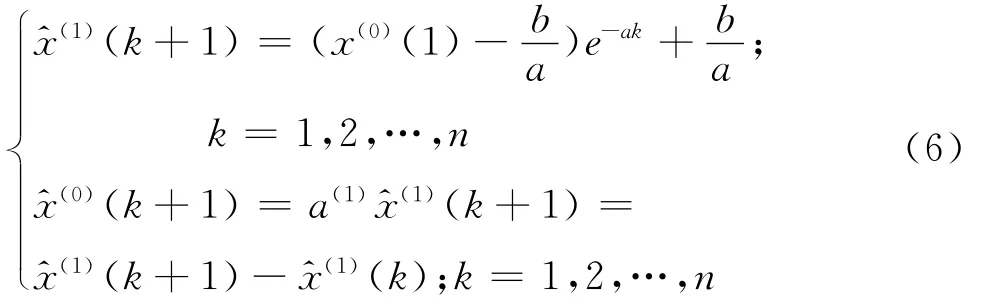
灰色预测模型GM（1，1）描述如下：将引信储存第1～n年可靠性实测数据作为一组时间序列X（0），对该组数列进行累加运算，淡化呈离散状态的原始数据随机性误差影响，显现其规律性，再以微分方程进行建模，使所建立的模型具有较高的精度，通过对模型值的还原，最终求得预测结果即为该批引信在第n＋1年时的可靠性预测值。

3 实例分析

本文引用参考文献［7］中对库存引信定期储存监测试验取得的作用可靠性数值，计算验证本模型。实测数值及年份对应关系如表1所示［7］。本文将储存4～7年的引信可靠性实测数据代入预测模型计算，求得第8年引信可靠性，并与原表中实测数据进行对比验证。

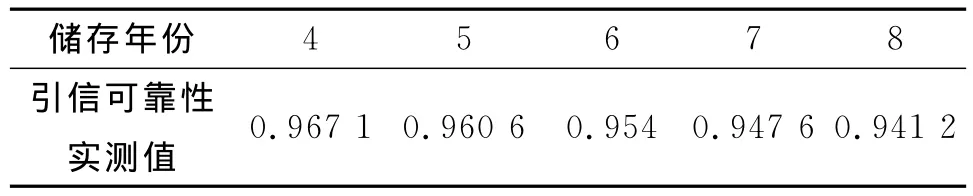
表1 引信储存年份与可靠性对照表Tab.1 Comparison table between fuze storage year and reliability

首先将储存4～7年的引信可靠性数据作为原始序列代入 GM（1，1）模型，得 X（0）＝ （0.967 1，0.960 6，0.954 0，0.947 6）；

求 X（0）的1－AGO数列可得X（1）＝ （0.967 1，1.927 7，2.881 7，3.829 3）；

X（1）的紧邻均值生成序列为：Z（1）＝ （1.447 4，2.404 7，3.355 5），于是：

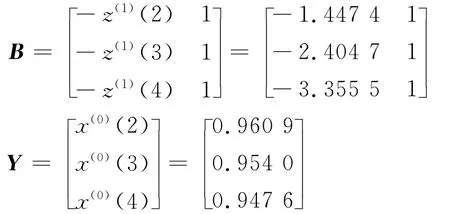
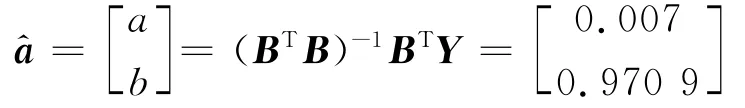
即a ＝ 0.007，b ＝ 0.970 9，取 x（1）（0）＝x（0）（1），则得到：

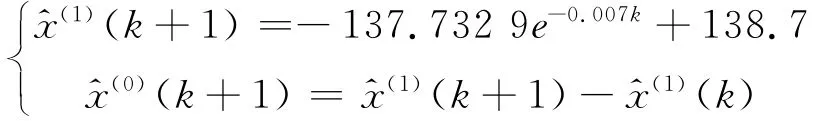
将k＝4代入并逐步计算，可得：

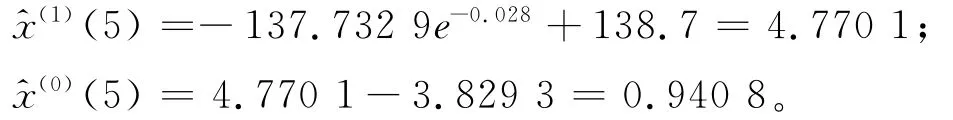
4 结论

本文将灰色理论引入引信储存可靠性预测。实例表明，该模型在对某批引信前4年储存可靠性实测数据进行加工处理的基础上，求解得到第5年可靠性预测值，与实测值基本一致，预测精度较高。应用该模型，可以较为准确地判断库存引信的质量状况及可靠性变化趋势，为生产厂家、使用部队提供相关辅助决策信息。

［1］吴晓颖，张万君.某型引信可靠性分配［J］.四川兵工学报，2010（12）：46－49.

［2］李晶，金韧.长贮环境对某引信钟表机构零件锈蚀影响分析［J］.国防技术基础，2010（9）：25－27.

［3］张亚，徐建军，赵河明.弹药可靠性技术与管理［M］.北京：兵器工业出版社，2001.

［4］Bruce L.Bowerman.Forecasting and time series［M］.北京：机械工业出版社，2003.

［5］邓聚龙.灰预测与灰决策［M］.武汉：华中科技大学出版社，2007.

［6］丁国勤.军队油料保障指挥决策模型研究［D］.重庆：重庆大学，2008.

［7］赵河明.基于神经网络的引信可靠性技术研究［D］.太原：中北大学，2005.