丛式井平台井口布置方法

闫 铁，徐 婷，毕雪亮，于 洋

（1.提高油气采收率教育部重点实验室（东北石油大学），黑龙江大庆 163318；2.吉林油田公司钻井工艺研究院，吉林松原 138000）

近年来，无论是陆上油田还是海上油田，应用常规直井或水平井开发常规油气资源的难度越来越大，丛式井由于具有投资小、见效快、便于集中管理等优点，已成为提高原油采收率和采油速率的有效手段，因而在常规／非常规油气资源开发中的应用日益增多[1］。平台优选是丛式井钻井的主要问题之一[2］，而关于平台井口位置与靶点的分配问题[3］，国内外学者以“水平位移之和最小”、“总井深之和最小”、“总井深与总水平位移之和最小”[4］等作为评价指标进行了相关的分析研究[5-6］，得出了一些有价值的结论。而在进行丛式井设计时，设计人员大多凭借经验对井口和靶点进行分配，没有科学的计算方法和手段。因此，笔者在借鉴前人研究成果的基础上，根据现场实际需要，对靶点的分配问题进行了研究，提出了井口与靶点的连线在水平面上的投影不相交且水平位移平方和最小的方法，即不相交水平位移最小距离法，为平台井口和靶点优选与分配提供了一种可行的方法。

1 靶点分配的数学模型

在论证平台位置优选可行性后，首先进行井口与靶点的分配，确定钻井顺序，进行井身剖面设计，因此，井口与靶点的分配是整个工程的关键，也是综合统筹的安排。在进行钻井设计时，提供的地质信息只有井口和靶点坐标，要进行井口和靶点的对应选择，需已知相邻多口井或平台井口及靶点信息，并进行优选，给出较为合理的、与井口对应的靶点。

优选时遵循的原则是，井口与靶点的连线在水平面上的投影不相交并使其水平位移平方和最小，即在多个井口及靶点组成的所有可能的连线中，选取在水平面上的投影互不相交并且水平位移平方和最小的井口与靶点的对应关系，即水平位移不相交最小距离法。

首先，要判断平台两口井的井口—靶点连线在水平面上的投影是否相交，已知一口井的井口坐标为（xp，yp），其对应的靶点为（xpt，ypt），另一口井的井口坐标为（xi，yi），其对应的靶点为（xit，yit），若则将结果保留为待优选的井口和靶点；若则需进一步判断交点是否在两条投影上，设交点为（x0，y0），约束条件为：

若满足式（1），则需换另一井口与靶点1连线组合重新计算，保留不满足式（1）的结果为待优选的井口和靶点。

再以井口和靶点连线水平投影平方和最小为优化指标，对以上保留的待优选井口和靶点建立如下约束优化模型，目标函数为：

式中：N为待优选的井口和靶点组合数；（xi，yi）为井口坐标；（xit，yit）为与井口对应的靶点坐标。

当井数量较多时，需要先将井口与靶点进行初始划分，将其划分为若干区域，使每一区域中的井口数量与对应的靶点数量（假设井口与靶点是一一对应的）在可应用全排列计算的范围之内，再进行井口—靶点划分。

2 靶点优选与分配流程

2.1 靶点分布划分

丛式井平台上井口多呈矩阵分布，如3排4列，5排10列等，由于靶点分布具有复杂性和多样性，将井口与靶点进行初始划分的方法有2种：一种是直线划分，另一种是同心圆划分。

2.1.1 直线划分

当井口分布为两排多列时，可用直线将井口划分为2部分，如图1所示（图中实心圆为井口，空心圆为靶点，同色即为初步待分配的井口和对应的靶点）。

图1 直线划分（靶点均分）Fig.1 Divide targets with straight line（uniform distribution of targets）

多个靶点在钻井平台周围大致呈均匀分布，但很难保证直线两侧的井口数量与靶点数量一定相等，可能会相差几个靶点。此时，需将直线两端向靶点较多的一侧弯折，将多出的靶点划分给另一侧。由于要使井口与靶点连线在水平面上的投影不相交，且成放射状分布，故只需将直线附近多余的靶点划分到另一侧即可，如图2所示（图中实心圆为井口，空心圆为靶点，同色即为初步待分配的井口和对应的靶点）。

图2 直线划分（靶点不均分）Fig.2 Divide targets with straight line（non-uniform distribution of targets）

2.1.2 同心圆划分

当井口分布为多排多列时，可将井口由外向里划分为若干环，靶点则按以平台中心为圆心的若干个同心圆划分，不断调整同心圆的半径，使两个同心圆之间的圆环所包含的靶点数量与对应井口环的井口数量相等，如图3所示（图中实心圆为井口，空心圆为靶点，同色即为初步待分配的井口和对应的靶点）。

图3 同心圆划分Fig.3 Divide targets with concentric circles

由于最外围的井口数量较多，需要进一步用直线划分，划分时保证井口与靶点为同一方向，用一条直线将井口与靶点同时划分。若一次划分不能满足要求，可进行多次划分，直到井口数量与靶点数量可应用全排列进行井口分配为止。具体划分如图4所示（图中实心圆为井口，空心圆为靶点，同色即为初步待分配的井口和对应的靶点）。

图4 同心圆与直线划分Fig.4 Divide targets with concentric circles and straight line

值得注意的是，靶点分布的实际情况很复杂，划分时不可避免地会出现个别特殊的现象，此时划分要灵活一些。例如，划分一般是由外向内进行，最外层井口与靶点的数量较多，但要保证井口数量与靶点数量相同，可能会存在个别井非最优方案，当划分较内层井口与靶点时，不一定要保证井口和靶点数量相同，以留有调整的余地。另外，考虑到井口分配从钻井平台中心向外辐射，若某靶点外围再无其他靶点，即使该靶点距离钻井平台很近，也可考虑划分为最外层。

3 井口与靶点优选分析

以2口井及2个靶点为例，介绍井口与靶点分配的计算分析过程。

已知井口1坐标A（x1，y1），靶点1坐标B（x2，y2），井口2坐标C（x3，y3），靶点2坐标 D（x4，y4）。并先选取井口1对应靶点1连线在水平面上的投影为AB，井口2对应靶点2连线在水平面上的投影为CD。

根据井口分配遵循的原则即水平位移不相交最小距离法，不相交可分为2种情况：1）AB、CD 平行，见图5（a）；2）AB、CD 不平行，但交点不在井口和靶点连线水平面投影上，见图5（b）。

图5 水平面上投影不相交的2种情况Fig.5 Two cases of disjoint wellhead－target trajectories on horizontal projection

判断模型为：

式（3）中：1）若d＝0，则投影AB和投影CD 平行或重合；2）若d≠0，则投影AB和投影CD 有交点或延长线有交点，假设交点为（x0，y0）。则：

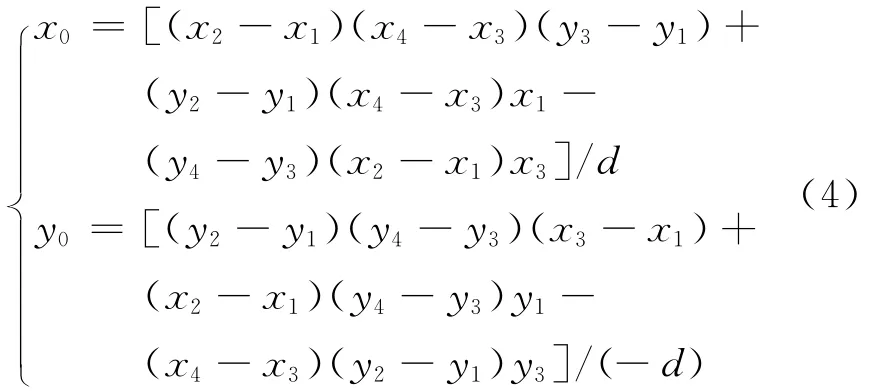
如需进一步判断交点是否在井口与靶点连线水平面投影上，约束条件为：

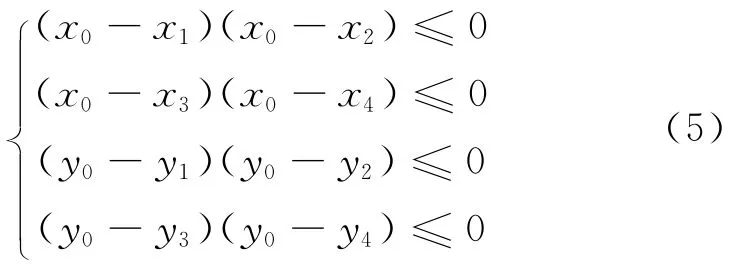
只有式（5）中的4个不等式都成立才可以判断（x0，y0）是投影AB和投影CD 的交点，如果有交点，则取井口1和靶点2、井口2和靶点1进行连线再次进行计算。如果这两组组合都没有交点，则取这两组组合中连线组合的最短距离。

则最短距离为：

所以最优组合为满足以上条件的井口靶点组合。

针对多口井多靶点的现场实际情况，经过直线或同心圆划分之后，即可依次循环以上分析计算过程。

4 实例计算

根据以上计算模型编制了平台井口和靶点优选计算软件。将靶点坐标、井口坐标和相应的数据输入计算软件，软件首先判断井口与靶点连线在水平面上的投影是否相交，在不相交的基础上，选择连线水平投影的最小距离，即完成了平台井口与靶点的优选与分配。以吉林某丛式井组为例进行计算。

已知5口井的井口坐标：1（0m，0m），2（4.66m，-1.81m），3（9.32m，-3.62m），4（13.98m，-3.62m），5（3.94m，6.20m），6（8.46m，4.41m），7（13.11m，2.57m）。

已知靶点坐标：a（-135.09m，-178.42m），b（-44.09m，-264.42m），c（81.91m，-188.42m），d（181.91m，-105.42m），e（-201.09m，-22.42m），f（-24.09m，-126.42m），g（80.91m，-28.42m）。

将井口与靶点坐标输入计算软件，即可计算出优选结果，结果如图6所示。

图6 靶点优选结果Fig.6 Optimized targetallocation

5 结论与建议

1）考虑丛式井平台井口和靶点的分配情况，提出了井口和靶点在水平面上的投影不相交且水平位移平方和最小的方法，并建立了丛式井平台井口和靶点优选与分配计算分析模型，编制了井口和靶点优选与分配分析软件，利用该软件可以快速求出平台井口和靶点最优分配结果，提高设计人员的工作效率。

2）通过实例计算可知，建立的分析模型能够满足现场要求，且该模型求解方便、快捷。但由于该模型对空间因素考虑较少，利用该模型分配井口和靶点时，还需要结合现场实际情况进行综合判断。

[1]Dogru S.Selection of optimum platform locations[J］.SPE Drilling Engineering，1987，2（4）：382-386.

[2]郭永峰，朱江，齐恒之.优选海洋平台钻井方式[J］.中国海上油气：工程，2002，14（5）：22-24.Guo Yongfeng，Zhu Jiang，Qi Hengzhi.New way to select model of drilling in offshore[J］.China Offshore Oil and Gas：Engineering，2002，14（5）：22-24.

[3]吴宏均，令文学，初永涛.吉林油田浅层丛式水平井井眼轨迹控制技术[J］.石油钻探技术，2011，39（5）：31-34.Wu Hongjun，Ling Wenxue，Chu Yongtao.Trajetory control technology for shallow cluster horizontal wells in Jilin Oilfield[J］.Petroleum Drilling Techniques，2011，39（5）：31-34.

[4]史玉才，管志川，陈秋炎，等.钻井平台位置优选方法研究[J］.中国石油大学学报：自然科学版，2007，31（5）：44-47.Shi Yucai，Guan Zhichuan，Chen Qiuyan，etal.Location optimization method for drilling platform[J］.Journal of China University of Petroleum：Edition of Natural Science，2007，31（5）：44-47.

[5]葛云华，鄢爱民，高永荣，等.丛式水平井钻井平台规划[J］.石油勘探与开发，2005，32（5）：94-100.Ge Yunhua，Yan Aimin，Gao Yongrong，etal.Drilling pad optimization for oilfield development by cluster horizontal wells[J］.Petroleum Exploration and Development，2005，32（5）：94-100.

[6]李文飞，朱宽亮，管志川，等.大型丛式井组平台位置优化方法[J］.石油学报，2011，32（1）：162-166.Li Wenfei，Zhu Kuanliang，Guan Zhichuan，etal.Location optimization for the drilling platform of large-scale cluster wells[J］.Acta Petrolei Sinica，2011，32（1）：162-166.