任意回转面叶型优化设计研究

□ 徐国华 □ 周正贵

南京航空航天大学 能源与动力学院 南京 210016

叶轮机内部通道内的流动实质上是空间三维性很强的有黏非定常流动，二维平面叶柵方法设计的叶型难以反映流动的三维性，用平面叶型积叠形成的叶片性能与预期会有一定差距［1］。根据吴仲华提出的三元流动理论，可以将叶片通道内流动分解为S1、S2两类流面流动［2］。但S1流面和S2流面都是三维空间曲面，这种方法实际应用相当复杂，因而通常作以下处理：假设流动轴对称，这时S1流面为任意回转面，因此可以用任意回转面方法进行叶型设计。

近年来随着计算流体力学技术的快速发展和优化控制理论的成熟，将优化控制技术与流场正问题计算相结合，自动进行叶型优化设计成为可能。自动优化设计的本质是由数学过程替代设计人员经验,控制设计参数修改方向，使设计过程更精确、严密，不但可以降低设计成本，而且提高设计效率［3］。国内外不少学者在叶型优化设计方面做了很多有意义的研究［3~9］，UFL Koller将正态分布随机搜索技术与叶型流场分析计算相结合，对高压级压气机叶型进行优化设计，优化后叶型性能明显提高［4］。国内有学者提出将单纯性法、序列二次规划等与遗传算法相结合，提高了遗传算法的局部寻优能力［5］。本文将改进后的遗传算法与NUMECA流场分析模块集成，实现多CPU高效并行、快速自动进行回转面叶型优化设计。

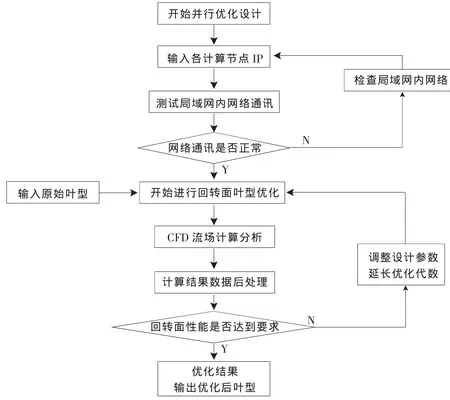
▲图1 优化系统运行流程图

1 自动优化设计软件研制

软件采用Visual C++6.0平台进行开发，整个优化系统使用C++和Fortran混合编写。由于MFC提供了功能强大的基础类库，使用C++可以方便实现数据通讯。软件界面采用CSplitWnd进行开发，Fortran主要用来开发叶型参数化模块和一些数据处理分析。优化系统包含的主要模块有：遗传算法模块、数据通讯模块、叶型参数化模块、NUMECA流场计算分析模块、计算结果数据后处理模块。由于CFD计算需要耗费大量的时间，所以优化系统采用并行技术，将不同的计算任务分发到不同的计算节点上，利用数据通讯和网络消息让各计算节点并行计算，缩短优化计算的耗时。

优化系统运行流程如图1所示，优化系统分为服务端软件和客户端软件。叶型优化进行前首先在所有客户端输入服务端IP连接到服务端，进行网络通讯测试，若不能正常通讯则应对网络硬件和软件环境进行检查，确保整个局域网能正常通讯。在服务端输入初始优化叶型，然后进行遗传算法参数、初始设计变量取值范围和适应度函数构造参数等设定，最后进行回转面叶型自动优化设计。优化系统在局域网内自动进行叶型优化设计，期间不需要人工对优化系统进行操作，若输出的优化叶型没有达到设计目标，优化系统则按照设定好的程序再次进行修改设计，直到输出符合要求的目标叶型，优化过程耗费时间的长短取决于优化问题的复杂度和局域网内参与计算的计算机节点的数目和性能。

1.1 遗传算法

遗传算法最早是密西根大学Holland教授于1975年提出，它是一种借鉴生物遗传和进化机制（优胜劣汰）形成的全局优化概率搜索算法。遗传算法的主要特点是:直接对设计变量进行操作，不需要求解导数；具有隐含并行性和全局寻优能力。因此遗传算法在组合优化、信号处理、人工生命等领域得到了广泛的应用。但用基本遗传算法求解多峰值函数的优化问题时存在早熟现象，搜索到的可能是局部最优值。但叶型气动优化恰恰是一个多峰值的优化问题，为了解决基本遗传算法的早熟问题，本文引入多种群技术。为了克服基本遗传算法二进制编码存在的海明悬岸问题，采用实数编码，采用非均匀交叉算子和非均匀变异算子进行遗传操作，以改善基本遗传算法的局部寻优能力。

为了测试改进后遗传算法的寻优能力，使用评价遗传算法性能的常用测试函数对改进后的遗传算法进行测试。本文选取Schaffer F7和Kursawe这两个典型的多维多峰值评价函数进行测试，用SGA表示基本遗传算法，用PGA表示改进后遗传算法。遗传参数选取如下：寻优终止代数为100，交叉概率0.8，变异概率0.01，优化 Schaffer F7函数种群大小为 20，优化Kursawe函数种群大小为60。两个测试函数独立进行50次寻优，将各自寻优获取的数值进行平均，得到的数据见表1。从表1可以看出，改进后的遗传算法性能得到了极大的提升。

表1 SGA和PGA函数测试结果

1.2 数据通讯

由于叶型优化设计变量数目较多，优化种群规模较大，因此有大量的个体需要计算。并且叶型网格生成和流场计算耗费时间较多，只有将这些不同的个体分配到不同的计算机节点上计算，这样构建的优化系统在时间上才具有工程实用价值。因此通讯模块保证数据高效稳定的传输在优化系统中起一个很关键的作用。

本文采用目前流行的TCP/IP通讯协议，该协议是一种面向连接可靠的通讯协议，因此能够保证数据可靠地在局域网内传输。微软为数据通讯提供了很多简单易用的API函数，利用这些API函数和MFC提供的相关类，可以开发出高质量的通讯模块，因此采用Windows Sockets API并基于CSocket进行网络通讯模块开发。通讯程序编写主要有两种模式：一种是C/S（客户端/服务器）模式，另一种是 P2P（Peer To Peer）模式。C/S模式是让某一个节点作服务端，其它节点是并行的作为客户端。在某一个计算节点上安装优化系统的服务端软件作为系统服务端，其它节点安装优化系统客户端软件作为客户端。服务端负责计算任务的分发和计算结果数据后处理，客户端负责计算服务端分配的计算任务，并将计算结果返回到服务端。本文采用典型的C/S模式进行通讯开发，应用C++语言进行程序编写，计算机节点间数据通讯流程如图2所示。

1.3 叶型参数化方法

叶型参数化方法要求能够合理地表达叶型，即：能够使表达的叶型具有足够的自由度，这样才能保证在这个足够大的空间中存在要寻找的叶型；尽量不要生成无效的叶型、负厚度叶型；在保证前两条的基础上尽可能使控制叶型的设计变量的数目少，因为设计变量太多，寻优空间大，增加寻优难度。

为此，本文采用基于修改量并用Bezier曲线表达修改量的参数化方法［10～11］。基于修改量的方法有许多优点：能够利用相对合理的初始叶型，在此基础上进行优化设计；可以控制所生成的叶型在一个合理的空间内变化；尽可能减少无效叶型的产生。图3是基于修改量方法的叶型参数化方法示意图，Δy表示修改量大小，y表示叶型型面厚度，s/s0是0到1的沿叶型弦长方向的无量纲数。本文用两条四阶Bezier曲线拟合叶型的吸力面和压力面的修改量曲线，将修改量叠加到原始叶型上，如图3（b）所示。在叶型前后缘用圆弧连接，这样处理既方便吸力面和压力面的修改，又能保证在前后缘处连接的合理性，为优化提供可靠方便的参数化模块。

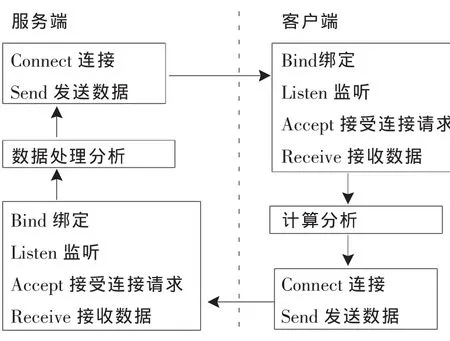
▲图2 计算机节点间数据通讯流程

2 任意回转面叶型的优化

应用研制的优化系统，对总压比为1.76、流量为6.27 kg/s压气机转子叶片进口70%叶高处回转面叶型进行了重新优化设计。原始回转面叶型进口相对马赫数为1.44，总压比为1.7。

优化系统为该回转面叶型设定的优化目标函数:

式中：C1、C2、C3为目标函数的权重系数；为效率；为目标总压比；为流场计算得到的总压比；m˙0为目标流量；m˙为流场计算得到的流量。

要求优化后叶型达到同样总压比、同样通流能力、等熵效率最高。回转面叶型设计变量的个数为12，种群规模为32，优化采用10个CPU，主频2.5 GHz共40个核，耗时30 h。

图4是优化前后叶型的对比，从图中可以发现，优化后叶型比较薄，相比较原始叶型，尾部有一定程度的上翘。表2表明优化后叶型设计点性能有大幅度提升，等熵效率提高了5.7个百分点，达到了优化目标。从图5叶型表面静压分布可以看出，优化后压力面第二道激波强度减弱。图6是优化前后叶柵通道马赫数等值线图，从图中可以看出，优化后叶型通道第二道激波强度都有下降，激波前马赫数从1.42下降到了1.15，并且尾部的分离明显减小。激波强度的减弱以及分离区的减小，都可以降低损失。

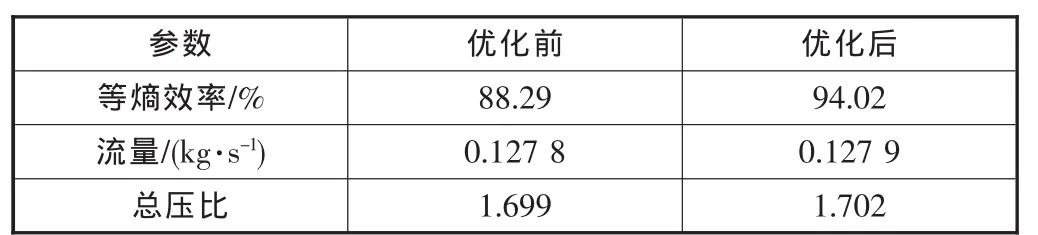
表2 超声速回转面叶型优化前后性能计算

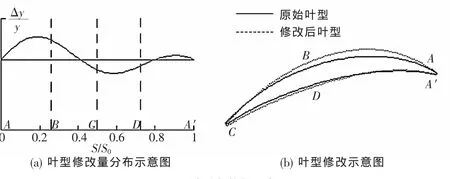
▲图3 叶型参数化示意图

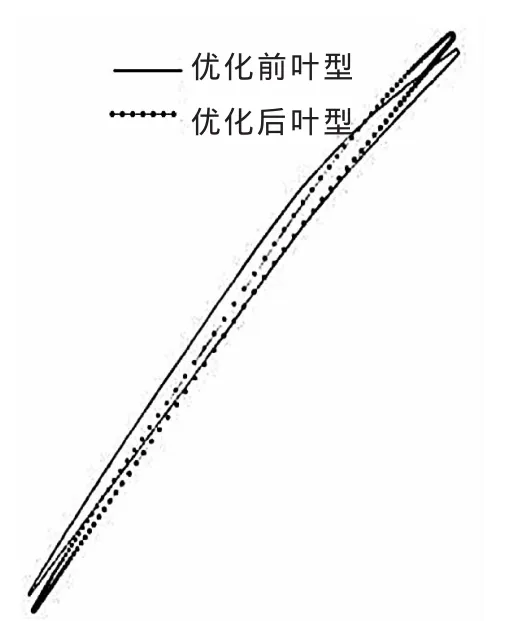
▲图4 原始叶型和优化后叶型

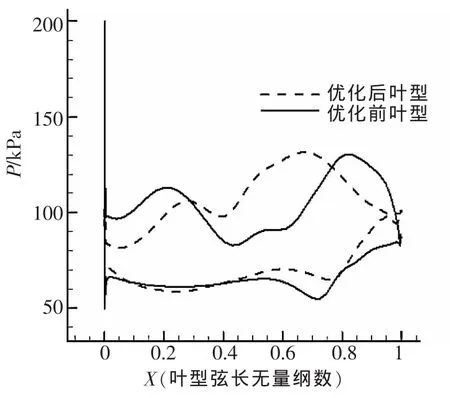
▲图5 优化前后回转面叶型表面静压分布

▲图6 回转面叶型优化前后马赫数等值线图

3 结论

1）将多种群技术与遗传算法相结合并采用实数编码，交叉算子和变异算子进行非均匀处理，改进后的遗传算法性能优异，全局寻优能力有大幅度的提升。

2）自主开发出回转面叶型优化设计系统，该系统将现代优化控制理论和CFD技术相结合，实现对回转面叶型的自动优化设计。

3）利用该优化设计系统对压气机回转面叶型重新优化设计，优化后的回转面叶型在流量和总压比大体保持不变的情况下，效率分别提升了5.7%。

［1］ 胡俊,吴铁鹰,曹人靖.航空叶片机原理［M］.北京：国防工业出版社,2006.

［2］ Wu Chung-Hua.A General Theory of Three-Dimensional Flow in Subsonic and Supersonic Turbomachines of Axial and Mixed-Flow Types ［Z］.National Advisory Committee for Aeronautics Technical Note，Washington,1952.

［3］ O.Lotfi,J.A.Teixeira,P.C.Ivey,et al.Aerodynamic Optimization of Industrlal Fan Blade Cascades［C］.ProceedingsofGT2005,ASME Turbo Expo 2005:Power for Land,Sea and Air,Reno-Tahoe,Nevada,USA,2005.

［4］ Ulf Koller, Reinhard Monig,Bernhard Kusters, et al.Development of Advanced Compressor Airfoils for Heavy-Duty Gas Turbines Part I:Design and Optimization ［J］.Journal of Turb-omachinery,2000,122 （3）:397-405.

［5］ 周正贵.压气机叶片自动优化设计 ［J］.航空动力学报，2002,17（3）:197-200.

［6］ Frank Sieverding,BeatRibi,Michael Casey,et al.Design of Industrial Axial Compressor Blade Sections for Optimal Range and Performance ［J］.Journal of Turbomachinery,2004,126（2）:323-331.

［7］ Bernhard Kusters,Heinz-Adolf Schreiber,Ulf Koller,et al.Development of Advanced Compressor Airfoils for Heavy-Duty Gas Turbines Part II:Experimental and Theoretical Analysis ［J］.Journal of Turbomachinery,2000,122（3）:406-415.

［8］ Toyotaka Sonoda,Yoshihiro Yamaguchi,Toshiyuki Arima,et al.Advanced High Turning Compressor Airfoils for Low Reynolds Number Condition Part I:Design and Optimization［J］.Journal of Turbomachinery,2004,126（4）:350-359.

［9］ Heinz-Adolf Schreiber,Wolfgang Steinert,Toyotaka Sonoda,et al.Advanced High Turning Compressor Airfoils for Low ReynoldsNumberCondition PartII:Experimentaland Numerical Analysis ［J］.Journal of Turbomachinery,2004,126（4）:482-492.

［10］ Farin，G.,Curves and Surfaces for Computer Aided Geometric Design［M］.London：Academic Press，1993．

［11］施法中.计算机辅助几何设计与非均匀有理B样条［M］.北京：高等教育出版社，2001.