质量度量指标驱动的数据聚合与多维数据可视化

李杨，郝志峰，谢光强，袁淦钊

(1.广东工业大学 自动化学院，广东广州510006;2.广东工业大学计算机学院，广东广州510006;3.华南理工大学计算机科学与工程学院，广东广州510006)

随着信息化社会的全面到来，面向高维海量数据的应用变得越来越普遍，因此，如何分析和使用这些数据是一个亟待解决的问题，鉴于人类对于海量高维数据的认知能力有限，在知识发现、信息决策的过程中，多维数据可视化技术成为一种辅助人们理解与直观地掌握数据特性的有效手段.多维可视化技术的目的是尽量反映多维信息及其各属性之间的关系信息，帮助数据工程师准确快速地发现数据集中隐藏的特征信息、关系信息、模式信息、趋势信息及聚类信息等.

然而，在对海量数据进行可视化时，情况更为复杂，应用传统的数据可视化技术及流程时，往往会出现图像叠加严重、可视化图像质量低、辨识性差等现实问题，数据聚合是解决该问题的一种有效方法，也就是在数据可视化之前先进行数据抽象.现有的数据聚合方法往往没有为数据可视化进行专门的优化和改进，更为重要的是，缺少针对可视化所作的数据聚合质量度量，对数据聚合的质量没有量化和理论支撑，本文研究的质量度量指标驱动的数据聚合弥补了上述不足.

为了弥补人类视觉感知能力的不足，帮助人们理解多维数据，研究人员提出了相当数量的数据可视化方法，这些方法将多维数据通过降维转换并映射到三维或者二维可视空间来实现多维信息的可视化.根据其可视化的原理不同可以划分为基于几何的技术、面向像素的技术、基于图标的技术、基于层次的技术、基于图形的技术和基于降维映射的技术等［1-2］.

在数据量较大时，为了提高数据可视化的图像质量，降低图像叠加的问题，通常会对数据进行抽象，数据抽象的目的是在数据精简的同时，保持原数据的各种特性，提高数据抽象后可视化的图像质量.抽样和聚合是2种常用的数据抽象方法.Bertini等［3］提出了利用聚类聚合的方法在散点图中自动降低图像叠加;Johansson等［4］提出了基于距离变化的数据抽样方法，并在屏幕空间对图像质量进行了度量.

质量度量的研究由来已久，随着数据可视化技术的发展，数据可视化中的质量度量越来越引起学者们的注意，越来越多的成果发表在数据可视化领域的重要期刊和会议上，这些方法也极大地促进了数据可视化技术本身的发展.根据数据可视化度量指标所实施的对象不同，现有的质量度量方法可以被分成两大类:实施于数据空间和图像空间［5］.在数据空间方面，Cui等［6］研究了在抽象和聚合2种不同的数据抽象方法下计算数据抽象质量，权衡如何在数据精简和数据损失方面取得平衡;在图像空间方面，Tatu等［7］使用Hough变换对感兴趣的散点图进行分级，以提高可视化图像质量.但是，图像空间的质量度量存在着受限于某种单个数据可视化方法的缺点.

本文提出一种数据空间质量度量驱动下的数据聚合方法均分K-means++，这一方法面向多维数据，广泛适用于大部分数据可视化方法，在质量度量指标的驱动下进行多维数据的可视化.

1 均分K-means++:一种多维数据可视化中的数据聚合方法

K-means算法具有简单、聚类速度快的优点.在大量的实验中发现，在进行海量数据的聚合运算中，K-means算法具有以下缺点:

1)在聚合运算，特别是海量数据的聚合运算中，K值往往较大，这种情况下，传统的K-means算法会出现迭代次数过大的情况，极大地影响了聚合速度.

2)传统的K-means++算法［8］虽然改进了初始点的选择，但仍然以最小化近邻点距离之和为目的，往往会出现各个聚簇的点数分布极不均匀的情况，某些聚簇只有几个点，某些聚簇则有成百上千个点.但是，在数据聚合中，往往希望聚合前的数据能在聚合后的各个中心点上均匀分布，使聚合后的数据更好地反映原数据的分布.

鉴于现有的K-means及其改进算法在数据聚合中存在的缺陷，本文提出了均分K-means++的数据聚合方法，仿真实验证明，该算法大大减少了迭代次数，在分布上与原数据更加吻合，从而更加适用于数据可视化中的数据聚合运算.

算法1 均分K-means

1)输入 d 维空间［0，1］d的 n 个点 p1，p2，…，pn，随机选择 k 个初始点 C={c1，c2，…，ck}.

3)对于1≤j≤k，计算集合 Sj内点之和 sum=∑i∈Sjpi和数目 num=|Sj|，cj=sum/num 为集合 Sj新的中心点.

4)重复2)～3)，直至C不再变化或迭代次数达到上限.

算法2 均分K-means++

令D(x)表示一个数据点到离它最近的已经选出的中心点的距离.则均分K-means++算法定义如下:

1)输入 d 维空间［0，1］d的 n 个点 p1，p2，…，pn.

①均匀随机地在X中选出第1个中心点.

③重复②，直至选出k个中心点.

2)继续算法1的2)～4)步.

2 质量度量指标驱动的数据可视化

数据可视化中的质量度量通常基于以下目的:寻找感兴趣的预测结果、降低图像叠加、发现有意义的模式等.近年来，虽然数据可视化中的质量度量研究发展很快，但很少有人将这些成果总结，并指出它们之间的联系，本文建立一个多维数据可视化质量评价模型，用来量化数据可视化中的聚合数据质量，从而驱动数据可视化图像质量的改善.

2.1 质量度量模型

可视化质量评价模型如图1所示.图中描述了质量评价模型下的数据可视化过程，包括3个阶段:

1)数据转换(源数据→转换后数据).数据转换的主要目的是改变数据形式为更利于可视化的格式，例如对于一些高维数据，需要进行特征选择、投影等降维操作，对于海量数据，常见的操作是聚合和采样.

2)数据映射(转换后数据→可视化结构).数据映射是整个模型的核心部分，这一步将数据的每一维表现为可视化结构中的可视特征.同样的数据可能映射为多种不同的可视化结构，质量评价指标需要对这些过程进行评价.例如，不同的维序对应不同的可视化结构，相应的质量度量评价也是不同的.

3)视图转换(可视化结构→视图).视图转换将可视化结构翻译为特定的图像形式(如像素)，这样做的目的是为了突出图像空间的作用，因为某些质量评价指标直接以可视化结构所对应的像素为计算对象，不过，相对于数据空间质量评价而言，直接对图像空间进行的质量评价相对较少.

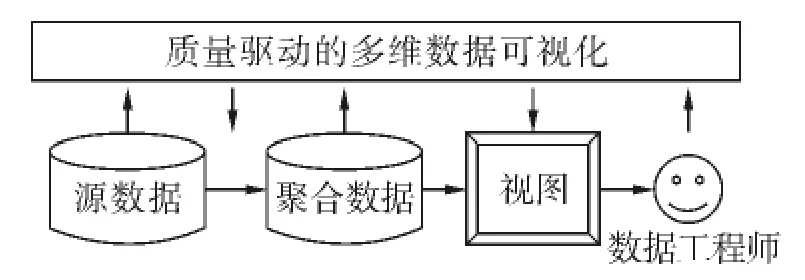
图1 总体框架Fig.1 Overall framework

质量评价模型可以帮助数据分析者选择一个可靠的过程组合.通常在一种情况下会有一个或者多个解决方案供数据分析者选择，整个选择过程都是由质量评价指标驱动的，因为质量评价指标可以量化每个阶段的数据或视图质量(向上箭头)，计算结果最终影响整个处理过程(向下箭头).

2.2 质量度量对象

根据数据可视化度量指标所实施的对象不同，现有的质量度量方法可以被分成两大类:实施于数据空间或图像空间.

1)数据空间.

在数据空间计算的度量指标只使用可视化前后的数据进行计算，不涉及到任何视图信息.

2)图像空间.

面向图像空间的度量指标计算则绕过数据，直接对输出的图像信息进行计算，这类方法通常需要辅助复杂的图像处理方法.

2.3 质量度量指标

1)聚类质量.

聚类质量指标用于度量可视化后的数据，保持分组信息的程度，对于明显分组的数据是否比较容易识别［9］.

2)相关性指标.

相关性指标用于度量可视化后的数据保持原数据二维或多维之间相关性的程度.二维数据之间的Pearson相关性和多维数据之间的全局相关性都在该指标考虑的范围之内［10］.

3)离群点指标.

离群点指标用于度量可视化后的数据保持那些与大部分其他数据明显不同的数据(即离群点)的能力［11］.

4)复杂模式指标.

Wilkinson等［12］提出一种度量发现复杂模式能力的指标，这些复杂模式不能在之前提出的分类中被发现，如“某种针织质地”、“某种身材指标”等.

5)图像质量指标.

图像质量指标不关心各种模式被保持的程度，而是度量可视化后的图像质量，例如图形是否大量重叠等.

6)特征保持指标.

特征保持指标度量可视化后的数据保持原数据特征的程度.这些特征包括原数据的分类信息［7，13］、可视化中的抽象数据相对于原数据而言的信息损失［3-4］等用户感兴趣的特征信息.

2.4 数据空间质量度量指标

图像空间中的质量度量对具体的数据可视化方法敏感，因此，本文选择的抽象数据级别(data abstraction level，DAL)、直方图差值度量(histogram difference measure，HDM)、最近邻距离度量(nearest neighbor measure，NNM)3个指标是数据空间中的质量度量指标，能够较好地验证算法2在聚类质量、图像质量和特征保持指标上的表现.

1)DAL.

DAL是数据抽象级别的缩写，用来表示数据抽象的程度，计算公式如式(1):

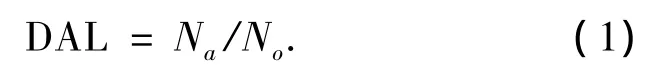
式中:Na表示抽象后的数据集大小，No表示原数据集的大小.

2)HDM.

HDM定义为抽象前后2个直方图的标准差，取值范围是［0，1］，0表示2个直方图所对应的每一对桶都有其中一个是空的，1则表示2个直方图所对应的每一对桶都完全一致，用式(2)来表示2个直方图第i个桶的差值:

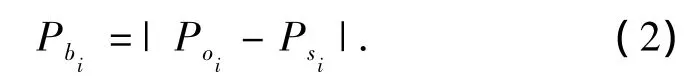
式中:Poi是抽象前数据落入第i个桶的比例，Psi是抽象后数据落入第i个桶的比例，Pbi是2个桶的差值.

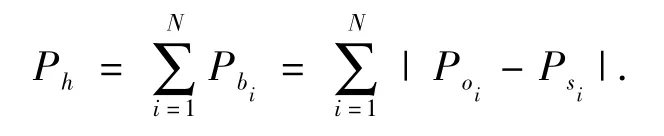
式中:Ph是2个直方图的差值，N是直方图中桶的数量.

如式(3)定义，HDM 是直方图标准差，Ph，max是 Ph最大值.

对于n维数据集的HDM定义为n个一维HDM平均值.默认的桶宽使用式(4)计算:

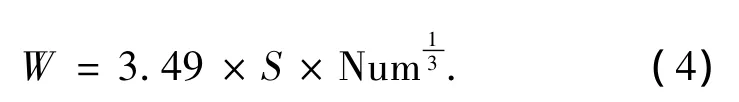
式中:S为某一维数据的标准差，Num为数据集的大小.

3)NNM.

NNM定义为每条记录与其抽象后代表它的记录之间的标准化距离平均值，计算公式如下:

①n维空间内2条记录U、V之间的欧氏距离为

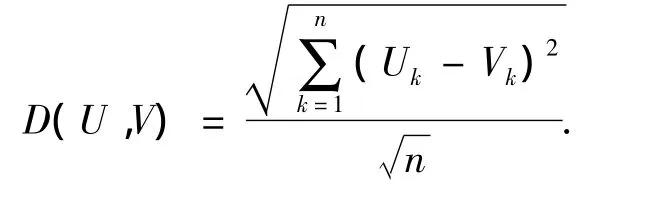
②对抽象前数据集中的第i条记录，计算它与抽象后数据集中每一条记录之间的距离，选择其中距离最小的值作为Di.

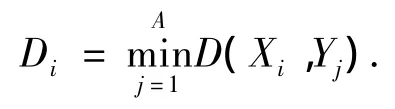
式中:Xi是抽象前数据集中的第i条记录，Yj是抽象后数据集中的第j条记录，A表示抽象后数据集的大小，Di代表第i条记录的距离.

③)标准化所有最小距离的平均值为NNM表示抽象前数据集的大小.

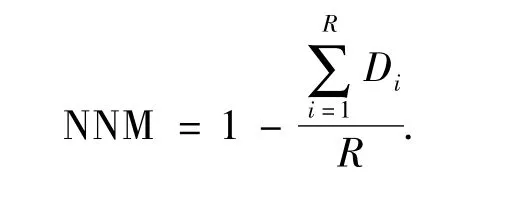
3 仿真实验

在几大类数据可视化方法中，基于几何的技术、面向像素的技术、基于层次的技术和基于图形的技术均适用于本文提出的方法.基于几何技术的基本思想是以点、线等几何画法将多维数据展现在二维、三维空间，适合于维数高但数据量相对不多的数据集，其代表方法为平行坐标法［14］，其他方法还包括放射坐标系［15］、散点图矩阵［16］、Andrews 曲线法［17］等.面向像素的技术利用像素的颜色代表数据的值，空间被分割成多个子窗口，每个子窗口对应多维数据中的一维，比较有代表性的方法包括VisDB［18］、圆形分段法［19］等.基于层次的技术可以对数据进行层次划分，将数据以层次结构的方式组织并以图形表示出来，在不同层次上表示不同维度的元素值，适用于每一维数据之间具有层次关系的多维数据.包括维堆［20］、嵌套坐标系［21］等方法.基于图形的技术利用图形的大小、颜色等属性表示数据，代表方法包括多线图、Survey Plot［22］，这 2 种方法都是在平行坐标法的基础上发展而来的.

上述的数据可视化方法的共同点是其可视化图像质量容易受到数据集大小的影响，因此，在应用本文提出的数据聚合方法时，既能够提高可视化图像质量，又能保持原数据的大部分特性.限于篇幅，本文只展示了2种最具代表性的数据可视化方法:平行坐标法和散点图法.

文中涉及的算法实现编程环境为MATLAB 7.1，数据可视化工具为XmdvTool［23］，实验环境为Windows XP 3.6GHz，2.00GB，实验中的所有数据都被规范化至［0，1］6，3个质量评价指标DAL、HDM、NNM的取值范围均为［0，1］.数据基本信息如表1所示.3.1 质量度量驱动的平行坐标图聚合前后对比

表1 实验数据信息Table 1 Experimental data

数据集DS1采用算法2分别以数据抽象级别DAL=0.07，0.04，0.02 时进行数据聚合.图2 包含了数据聚合前后的平行坐标图，可以发现，在DAL=1，即数据聚合前，数据叠加严重，难以辨识其中任何的数据，而聚合后的数据不仅保持了较高的质量度量指标(如图3所示)，图像质量也有了明显的提高.

图2 不同DAL下DS1的平行坐标图Fig.2 Parallel coordinates of DS1at different DALS

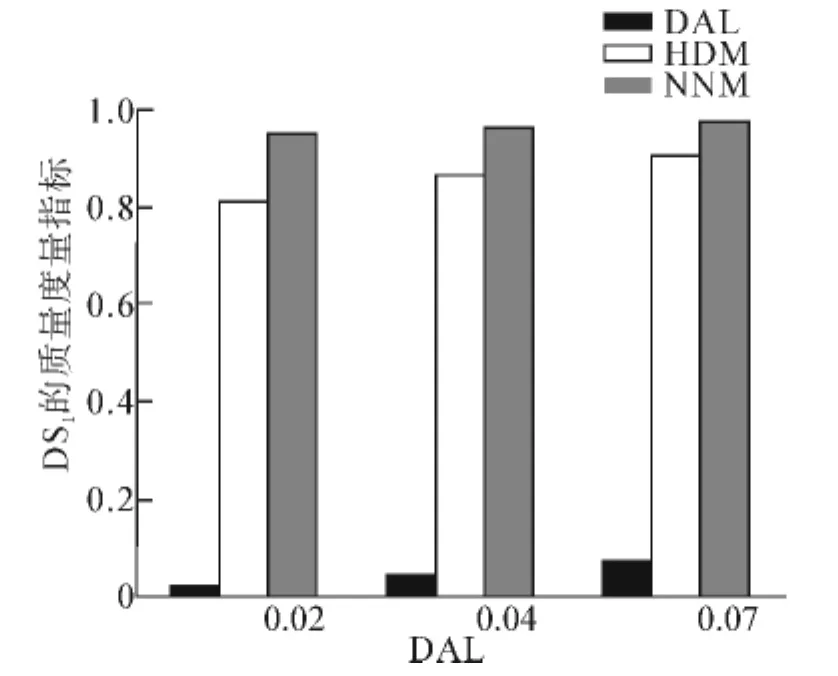
图3 不同DAL下DS1的质量度量指标Fig.3 Quality metrics of DS1at different DAL

3.2 质量度量驱动的散点图聚合前后对比

图4是数据集DS2用算法2进行数据聚合前(DAL=1)及聚合后(DAL 为0.02，0.04，0.07)的散点图矩阵.不难发现，在DAL=1时，各个数据点叠加严重，很难辨识其中的任何有用信息，也难以发现两维属性之间的关系，而聚合后的数据即使在DAL=0.02时，也能很容易地发现其中存在的属性关联信息.图5展示了聚合后的DS2同样保持了较高的质量度量指标.当数据维度较小时，聚合后的数据在散点图上的表现更好.

图4 不同DAL下DS2的散点图Fig.4 Scatter plots of DS2at different DAL

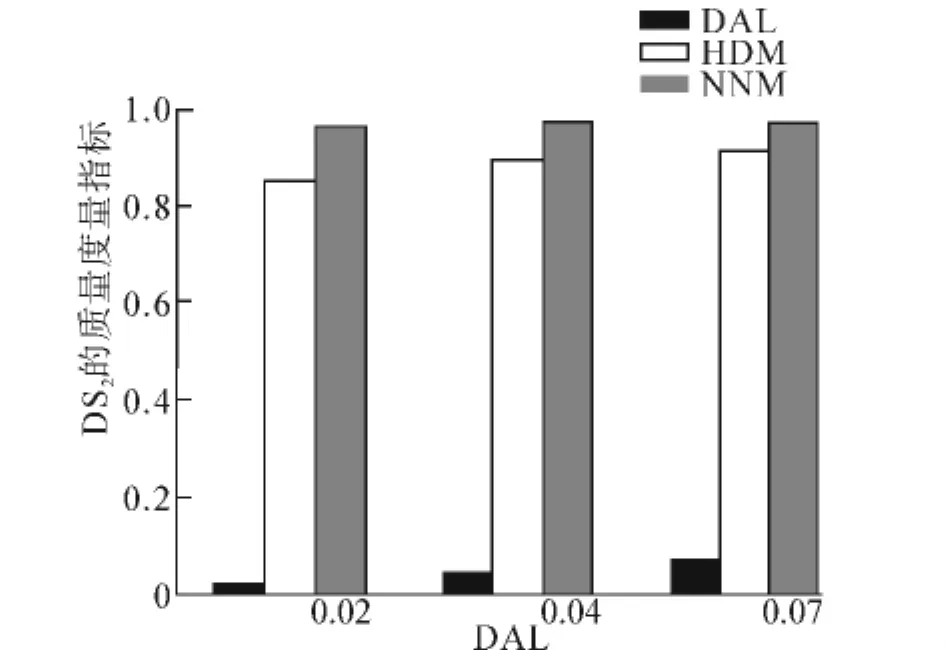
图5 不同DAL下DS2的质量度量指标Fig.5 Quality metrics of DS2at different DAL

4 结束语

质量度量指标驱动下的数据聚合加入了质量量化指标，聚合数据的质量可以被精确量化，可以帮助数据工程师在数据可视化的过程中根据实际需求调整度量指标参数，以获取聚合数据质量与可视化图像质量之间的平衡.本文提出了一种均分K-means++数据聚合算法，仿真实验表明，与传统的聚类算法相比，均分K-means++更适用于以提高数据可视化图像质量为目的的数据聚合.目前，均分K-means++数据聚合算法存在的问题是当K增大到一定程度时，初始点的计算效率较低，下一步将研究如何在海量数据集上提高算法效率.

［1］孙扬，封孝生，唐九阳，等.多维可视化技术综述［J］.计算机科学，2008，35(11):1-7.SUN Yang，FENG Xiaosheng，TANG Jiuyang，et al.Survey on the research of multidimensional and multivariate data visualization［J］.Computer Science，2008，35(11):1-7.

［2］KEIM D A，ANKERST M.Visual data mining and exploration of large databases［C］//PKDD.Freiburg，Germany，2001:104-109.

［3］BERTINI E，SANTUCCI G.Quality metrics for 2D scatterplot graphics:automatically reducing visual clutter［C］//Smart Graphics 4th International Symposium.Banff，Canada，2004:10-15.

［4］JOHANSSON J，COOPER M.A screen space quality method for data abstraction［J］.Computer Graphics Forum，2008，27(3):1039-1046.

［5］BERTINI E，TATU A，KEIM D.Quality metrics in highdimensional data visualization:an overview and systematization［J］.IEEE Trans on Visualization and Computer Graphics，2011，17(12):2203-2212.

［6］CUI Q，WARD M，RUNDENSTEINER E，et al.Measuring data abstraction quality in multiresolution visualizations［J］.IEEE Trans on Visualization and Computer Graphics，2006，23(12):709-716.

［7］ALBUQUERQUE T A，EISEMANN G.Combining automated analysis and visualization techniques for effective exploration of high-dimensional data［C］//Proc IEEE Symp Visual Analytics Science and Technology.Atlantic City，USA，2009:59-66.

［8］ARTHUR D，VASSILVITSKII S.K-means++:the advantages of careful seeding［C］//Symposium on Discrete Algorithms.Philadelphia，USA，2007:1027-1035.

［9］FERDOSI B J，BERNOULLI J.Finding and visualizing relevant subspaces for clustering high-dimensional astronomical data using connected morphological operators［C］//IEEE Conf Visual Analytics Science and Technology.Salt Lake City，USA，2010:35-42.

［10］JOHANSSON S，JOHANSSON J.Interactive dimensionality reduction through user-defined combinations of quality metrics［J］.IEEE Trans on Visualization and Computer Graphics，2009，15(6):993-1000.

［11］PENG W，WARD M O，RUNDENSTEINER E A.Clutter reduction in multi-dimensional data visualization using dimension reordering［C］//IEEE Symp Information Visualization.Austin，USA，2004:89-96.

［12］WILKINSON L，ANAND A，GROSSMAN R.Graph-theoretic scagnostics［C］//IEEE Symp Information Visualization.Chicago，USA，2005:157-164.

［13］SIPS M，NEUBERT B，LEWIS J P，et al.Selecting good views of high-dimensional data using class consistency［J］.Computer Graphics Forum，2009，28(3):30-41.

［14］INSELBERG A.The plane with parallel coordinates［J］.The Visual Computer，1985，1(2):69-91.

［15］HOFFMAN P E，GRINSTEIN G G，MARX K，et a1.DNA visual and analytic data mining［C］//IEEE Visualization Phoenix.Phoenix，USA，1997:437-441.

［16］MATRIX S.Scatter plot matrics［EB/OL］.［2012-09-20］.http://www.itl.nist.Gov/div898/hand book/eda/section3/eda33qb.html.

［17］ANDREWS D F.Plots of high-dimensional data［J］.Biometrics，1972，28(1):125-136.

［18］KEIM D A，KRIEGEL H P.VisDB:database exploration using multidimensional visualization［J］.Computer Graphics Applications，1994，14(5):40-49.

［19］HOFMAN P E.Table visualizations:a formal model and its applications［D］.Lowell，USA:University of Massachusetts，1999:25.

［20］WARD M O，LEBLANC J，TIPNIS R.N-Land:a graphical tool for exploring n-dimensional data［C］//Computer Graphics International Conference.Melbourne，Australia，1994:1-14.

［21］FEINER S，BESHERS C.Worlds within worlds:metaphors for exploring n-dimensional virtual worlds［C］//ACM Proceedings Conference on User Interface Software Design.New York，USA，1990:76-83.

［22］LOHNINGER H.INSPECT，a program system to visualize and interpret chemical data［J］.Chemometrics and Intelligent Laboratory Systems，1994，22(1):147-153.

［23］WARD M O.“Xmdvtool”［EB/OL］.［2012-09-23］.Xmdv Users Group.http://davis.wpi.edu/xmdv/datasets.html.