基于大脑情感学习的四轮驱动机器人速度补偿控制

陈建平，王建彬，杨宜民

(1.肇庆学院计算机学院，广东 肇庆526061;2.广东工业大学自动化学院，广东 广州510090)

全向移动机器人具有全方位移动的功能，可以在不改变位姿的情况下向任意方向运动，凭借独特的运动优势，在国内外中型组机器人大赛中，得到了大力的推广和发展，但其复杂的轮系分布给机器人的控制带来了难度［1］.机器人受到堵转、摩擦、打滑及各种扰动因素的影响，导致机器人的运动能力变差而偏离目标点，控制精度不高［2］.因此，大多数研究是从如何改善各个轮的驱动控制环的动态性能出发，通过各种先进的控制与补偿技术提高对每个轮驱动电机的控制精度，然而这种方法没有考虑机器人整体的速度跟踪误差［3-7］.

文献［8］依据交叉耦合思想设计了2轮差动机器人的速度补偿控制器，但是难以应用到相对复杂的全向移动机器人运动控制中.文献［9］为提高机器人灵巧手基关节的轨迹跟踪精度，提出了包含同步误差和位置误差反馈项及平滑鲁棒非线性反馈补偿项的交叉耦合同步控制策略，由于该方法需要复杂的计算求解，导致很难满足全向移动机器人运动控制的实时性要求.文献［10］基于模糊控制与PD控制理论设计了一种速度补偿控制器，对机器人4个轮子的速度进行补偿，由于控制规则要靠经验确定，参数变化缺乏自适应和自学习能力，控制过程中存在死区，导致机器人在速度较大时控制偏差变大而得不到及时调整，甚至出现失控现象.

针对上述方法的不足，本文提出了一种基于大脑情感学习的4轮驱动机器人速度补偿控制方法.利用大脑情感学习能力强、计算简单的特点［11-12］，对机器人整体的速度误差设计合理的误差补偿器，在不改变机器人内部控制结构的情况下，为机器人4个轮子提供附加的补偿控制量，进而提高机器人整体的运动控制精度.

1 全方位移动机器人运动学模型

建立4轮全方位移动机器人的轮系分布系统，如图1所示［13］.由于所用比赛足球机器人的射门机构的增加，导致4个全向轮不是对称分布，而是前2轮夹角为120°，后2轮夹角为90°.

图1 机器人运动学模型Fig.1 Kinetic model of the robot

根据图1所示，建立机器人运动坐标系，XOY为世界坐标系，xoy为以机器人中心为原点的局部坐标系，得到机器人运动学方程为

式中:θ为机器人的运动方向;vθ为机器人的角速度，逆时针方向为正;v1、v2、v3、v4分别为4 个车轮的线速度;δ1和δ2为各轮与x轴的夹角;L为车体中心到轮子中心的距离.

车轮的线速度和角速度之间的关系如式(2):

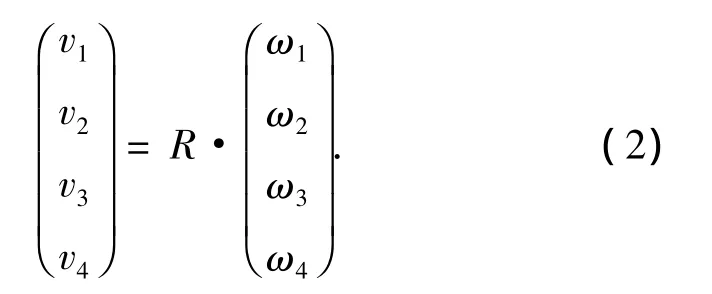
式中:R 为轮子半径;ω1、ω2、ω3、ω4为轮子角速度，逆时针方向为正.

2 四轮驱动机器人的速度补偿控制系统

根据机器人足球比赛的实际需要，设计4轮驱动足球机器人的速度补偿控制系统，其结构框图如图2所示.

图2 机器人的速度补偿控制系统结构Fig.2 Structure of velocity compensation controller for the robot

由图2可知，将实际测得的机器人整体的实际速度与其参考速度进行比较，经过速度补偿控制器处理后得到4个轮子关于机器人整体速度误差的额外补偿量.从而在不改变各轮子内环控制结构的前提下，实现了对机器人整体速度的有效补偿，提高了系统运动控制的精度.

3 基于大脑情感学习的速度补偿控制

3.1 大脑情感学习计算模型

Moren等于2000年提出了基于神经生理学的大脑情感学习(brain emotional learning，BEL)计算模型［11］，该模型在不完全模仿杏仁核、眶额皮质等生理结构的基础上，将大脑情感学习模型划分为两大组成部分，即分别对应杏仁核和眶额皮质.大脑情感学习模型的基本工作原理及结构如图3所示.

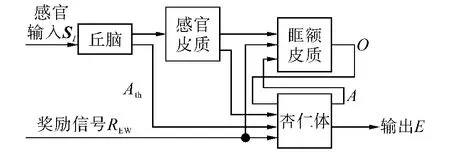
图3 大脑情感学习模型的基本结构Fig.3 Structure of brain emotional learning model

由图3可知，感官输入信号SI的最大值通过丘脑传递给杏仁体，则有Ath=max(SI).

1)对于每一个刺激信号，杏仁体内均有一个对应节点Ai来接收，该刺激信号包括感官输入信号SI、奖励信号REW以及丘脑信号Ath，则杏仁体的输出为

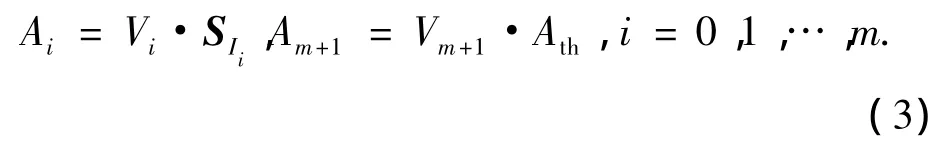
式中:m为刺激信号的数目，Vi为各节点的权值，其调节律为:

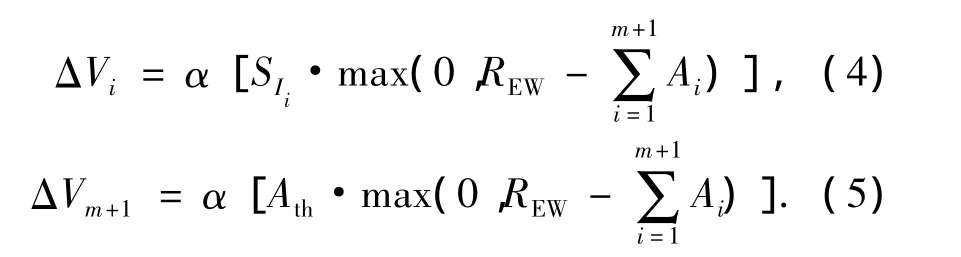
式中:α为学习率，它影响杏仁体的学习速度;ΔVi的单调性与SIi的符号保持一致.

2)对于刺激信号，眶额皮质内也有节点接收，它的刺激信号为感官皮质信号(即感官输入信号)和来自杏仁体的信号，而对丘脑的信号不产生刺激.它的输出为

式中:Wi为各节点的权值，它的调节律为

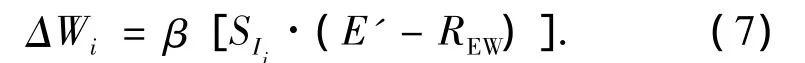
式中:β为学习率，且β＞0，E'为不含丘脑信号刺激下的杏仁体的输出，可表示为

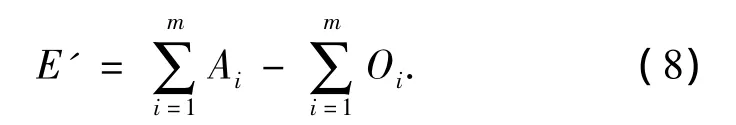
由式(3)～(8)可以看出，ΔWi可取正值也可取负值，即眶额皮质能抑制或增强杏仁体的学习过程，通过消除奖励信号REW与杏仁体输出E'之间的差值，使杏仁体向着期望值学习.

3.2 基于大脑情感学习的速度补偿控制器

BEL模型与实际系统相结合，必须事先确定感官输入信号SI和奖励信号REW的函数形式，分别称之为感官输入函数和情感暗示函数，它们为系统的输入与输出、控制量以及跟踪误差等因素的函数.因为A-O组织中的可调权值较多，其节点个数通常设置为多个，因此，感官输入函数通常为向量形式.

由于全向移动机器人的角速度可以单独进行规划，此处只讨论机器人的线速度补偿控制器.又由于机器人在局部坐标系的x和y方向上有相似的运动特性，因此本文以x方向上的线速度为例设计补偿控制器.基于大脑情感学习的速度补偿控制器结构如图4所示.

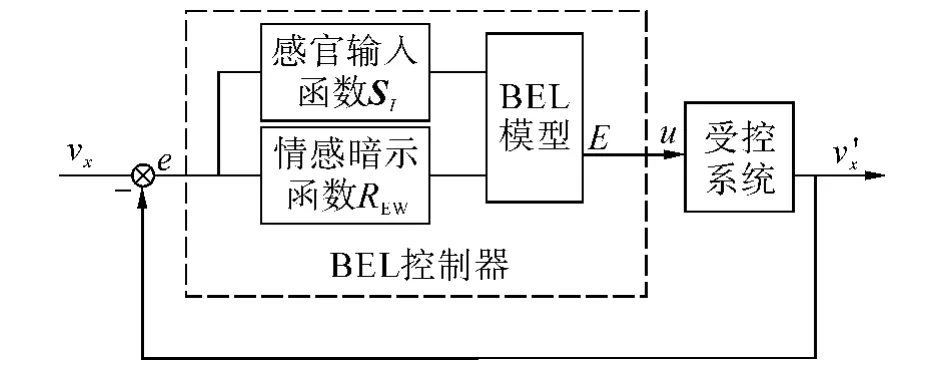
图4 基于大脑情感学习的速度补偿控制器Fig.4 Velocity compensation controller based on brain emotional learning

设x方向机器人的线速度误差为e，为了便于与文献［10］中的方法进行比较，选取感官输入函数为PID控制器的形式，则有感官输入函数为

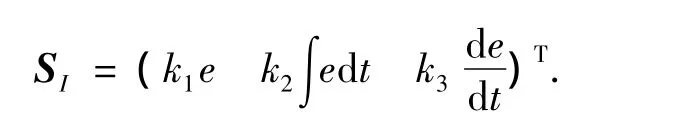
以刺激学习的奖励信号REW为目标函数的情感暗示函数为

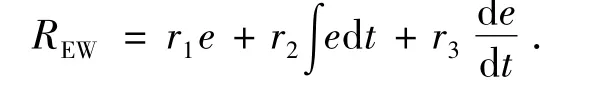
则有BEL模型的输出为

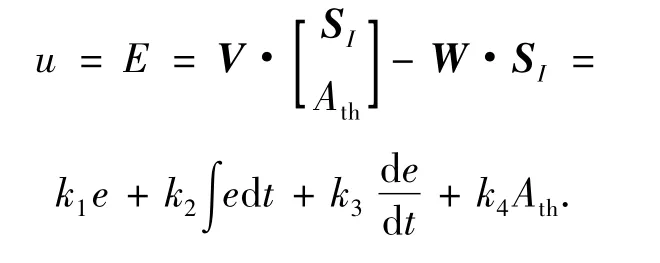
式中:k1、k2、k3、k4、r1、r2、r3分别为权重调节系数，r1、r2、r3为对象误差减小的期望.k1～k4的调节律为:

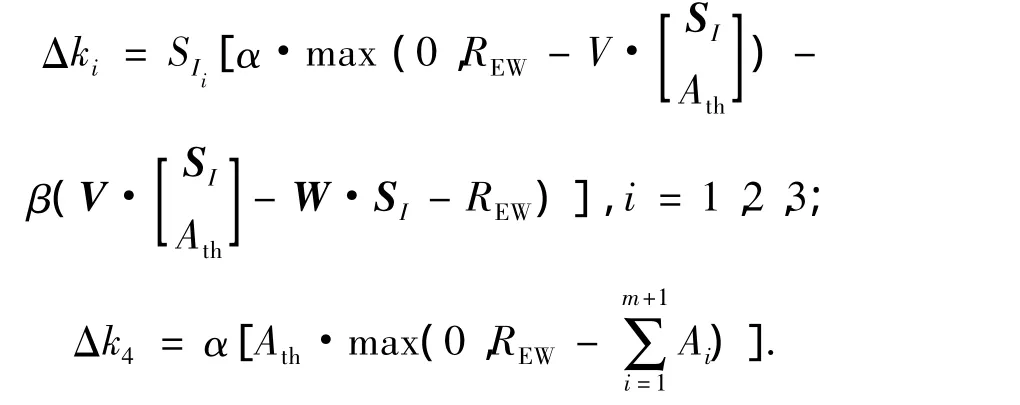
式中:SIi表示SI中的各个向量元素.

通常，神经网络学习需要利用系统的导数信息，按照梯度下降的思想进行权值的更新迭代，易受到初始取值的影响，计算效率低;而由权值调节式(4)、(5)和(7)可知，本文设计的控制器在运行时，不需要具体的导数信息就能够实现各个权值系数的迭代更新，对初始值的选取不敏感，计算效率高，这也是该方法与神经网络学习的本质区别.同时，该控制器直接以误差的PID控制函数形式作为奖励信号函数，从而保证了控制系统的稳定性.

4 仿真实验及结果分析

为验证本文所提方法的有效性，进行了机器人路径跟踪仿真实验，令机器人跟踪x方向的直线路径.实验过程中，分别采用无速度补偿控制(NVCC)、模糊 PD 速度补偿控制(FUPD)［10］以及本文方法(BELVC)进行仿真.

以实验室的“太极队”中型组足球机器人作为研究对象进行仿真实验研究，机器人轮子直流电机的具体性能参数设置情况详见文献［13］.BEL控制器的基本参数初始值设定为k1=10、k2=0.5、k3=0.01、r1=1 300、r2=25 000、r3=10.

4.1 学习率对系统的影响

当学习率α、β取不同的数值情况时(分别为方案1:α =0.001，β =0.02;方案 2:α =0.001，β =0.035;方案 3:α =0.005，β =0.015;方案 4:α=0.000 5，β =0.001)，系统的阶跃响应如图 5 所示.

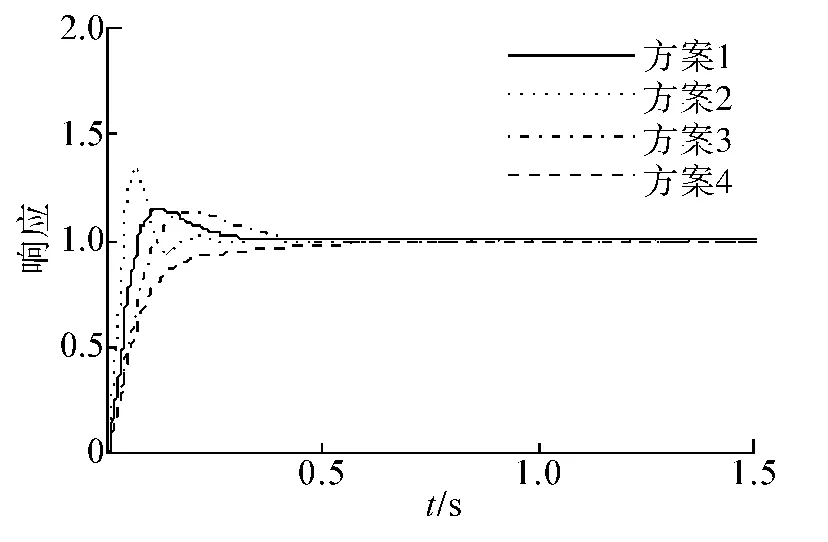
图5 不同学习率情况下的系统响应Fig.5 System response in different learning rate situations

由图5可知，当BEL控制器的基本参数不变时，权值学习率α、β的选取对控制器响应结果的影响非常明显.当α的值恒定时，β的值越大，系统响应越快，但是系统的振荡幅度越大，系统达到稳定状态的时间越长;当α、β的取值同时减小时，系统的振荡幅度也减小，当α、β的取值继续减小时，则系统达到稳定状态需要更长的时间.

4.2 机器人速度与轨迹跟踪

实验中，选取第1组学习率参数方案进行控制，即取 α =0.001、β=0.02.为了更好地研究BEL 控制器的优越性，当t=2 s时，在给定的输入信号中加入扰动，所得到的机器人1号轮子(由于本实验室所用4轮机器人的4个电机参数相同，因此在进行仿真时仅给出了1号轮子的仿真曲线，其他3个轮子与之相似，故作省略)的速度跟踪曲线以及机器人整体的轨迹跟踪结果分别如图6～8所示.

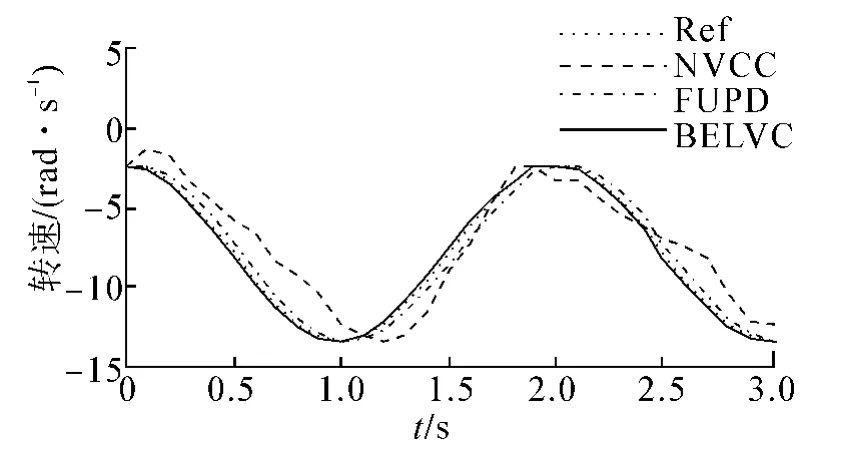
图6 1号电机无扰动时的速度跟踪曲线Fig.6 Velocity tracking curve of the No.1 motor without interference

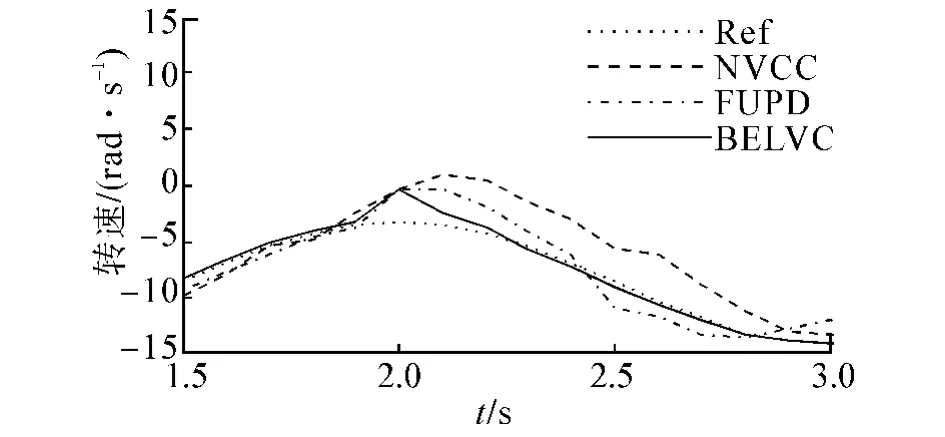
图7 1号电机有扰动时的速度跟踪曲线Fig.7 Velocity tracking curve of the No.1 motor with interference

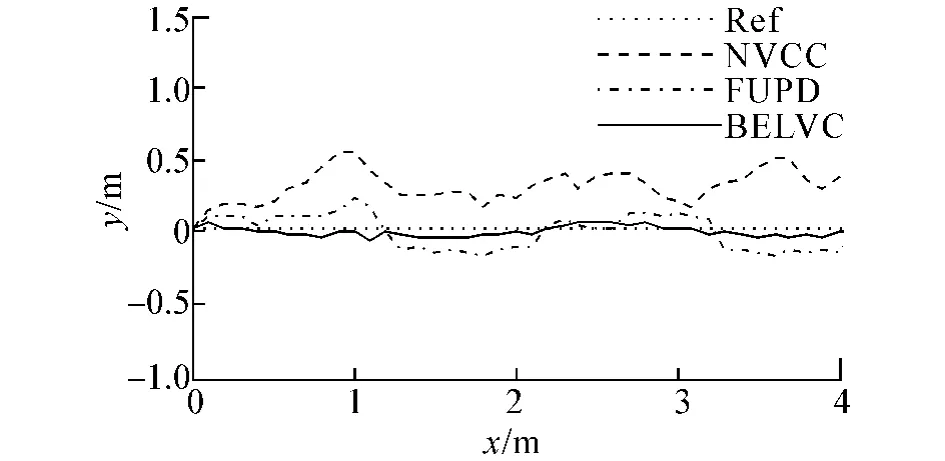
图8 机器人整体的轨迹跟踪曲线Fig.8 Trajectory tracking curve of the robot

表1所示为采用不同控制方法时，机器人轨迹跟踪的最大偏差与平均偏差的对比统计情况.

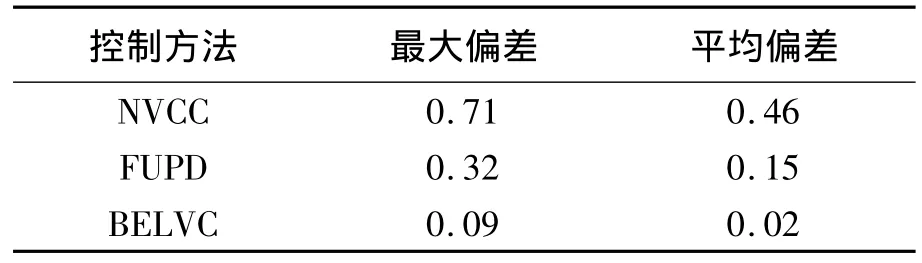
表1 机器人轨迹跟踪偏差比较Table 1 Comparison of trajectory tracking error m

由图6～8可以看出，在机器人未采用速度交叉耦合补偿时，由于场地材料不同、4个轮子装配上存在误差、轮子与场地之间摩擦力不一致、4个驱动电机存在机械差异等原因，使得机器人在加速过程中4个轮子的加速程度不一致，同时也使得4个轮子的转速与其期望值之间存在较大偏差，机器人很难跟踪预先期望的运行轨迹;当采用模糊PD控制方法时，由于模糊规则建立的主观性，参数变化缺乏自适应和自学习能力，控制过程中容易出现控制死区的现象，导致机器人在速度较大时控制偏差变大而得不到及时调整，机器人4个轮子的转速出现较大幅度的波动，跟踪轨迹的精度变差，并且当机器人的速度越大时，轨迹跟踪的偏差也越大，甚至会出现失控的现象;当采用本文所设计的方法BELVC进行控制时，4个轮子速度跟踪的波动明显减小，从而使得机器人的运行轨迹更加接近期望轨迹.

由图7可知，当系统出现外界扰动的情况下，BEL控制器的反应比模糊PD控制器的反应更快，输出响应曲线更平滑，系统更稳定，减小了外界扰动对系统的影响，从而使控制系统呈现出良好的鲁棒性.同时，由表1可知，在进行轨迹跟踪时，采用本文设计方法BELVC的情况下，机器人轨迹跟踪的最大偏差和平均偏差均小于其他2种方法.由此，进一步验证了本文设计方法BELVC确实提高了机器人轨迹跟踪的精度.

5 结束语

由于全向移动机器人复杂的机械结构，其4个轮子之间存在着耦合关系，即使单个电机的控制参数达到最优，整个机器人的控制效果也未必理想.同时，由于4个驱动电机的参数不一致、负载的扰动、各个轮子安装时的机械差异等种种因素的影响，不可避免地将会导致机器人在运动过程中，其实际位姿和期望位姿之间存在偏差.引入本文的基于大脑情感学习的4轮驱动机器人速度补偿控制器以后，将机器人整体的速度误差转换为4个轮子转速的额外补偿量，在不改变机器人内环电机转速控制结构的情况下，通过大脑情感学习模型内部各节点权值的在线学习，及时地调整4个轮子的转速，有效地减小了机器人整体的速度误差，进一步提高了其轨迹跟踪的精度，从而改善了机器人的运动性能.然而，本文中BEL控制器各相关参数的选取主要是在仿真环境下采用试凑法获得的，有关算法的收敛性以及学习率取值的定量分析等问题将在今后工作中做进一步研究.

［1］EFENDI M S，MOHAMED R，SAZALI Y.Designing omnidirectional mobile robot with mecanum wheel［J］.American Journal of Applied Sciences，2006，3(5):1831-1835.

［2］BAHAA I K，ALI H H，MUSTAFA M M.Modified vector field histogram with a neural network learning model for mobile robot path planning and obstacle avoidance［J］.International Jouranl of Advancements in Computing Technology，2010，2(5):166-173.

［3］ALI H H，FATIMA B I.Path lanning of mobile robot based on modification of vector field histogram using neuro-fuzzy algorithm［J］.International Journal of Advancements in Computing Technology，2010，2(3):129-138.

［4］MARYAM R，MOHAMMAD H K，MOHAMMAD A N，et al.Designing the fuzzy controller in mobile robot navigation with the presence of unknown obstacles［J］.International Journal of Intelligent Information Processing，2012，3(1):45-62.

［5］ALBERTO V，CARL T，BENGT L，et al.Modeling and optimization of energy consumption in cooperative multi-robot systems［J］.IEEE Transactions on Automation Science and Engineering，2012，9(2):423-428.

［6］ELEFTHERIA S S，GEORGE S S，ANASTASIOS D P.Optimal robot speed trajectory by minimization of the actuator motor electromechanical losses［J］.Journal of Intelligent and Robotic Systems，2002，33:187-207.

［7］熊蓉，张翮，褚健，等.四轮全方位移动机器人的建模和最优控制［J］.控制理论与应用，2006，23(1):96-98.XIONG Rong，ZHANG He，CHU Jian，et al.Modeling and optimal control of omni-directional mobile robots［J］.Control Theory and Applications，2006，23(1):96-98.

［8］曹洋，徐心和.一种基于交叉耦合的速度控制器［J］.东北大学学报，2003，24(5):420-423.CAO Yang，XU Xinhe.Cross-coupling speed controller［J］.Journal of Northeastern University，2003，24(5):420-423.

［9］兰天，刘伊威，陈养彬，等.机器人灵巧手基关节交叉耦合同步控制［J］.机器人，2010，32(2):150-156.LAN Tian，LIU Yiwei，CHEN Yangbin，et al.Synchronized cross-coupled control for base joint of dexterous robot hand［J］.Robot，2010，32(2):150-156.

［10］匡建辉，杨宜民.基于模糊PD控制的四轮驱动全向移动机器人速度补偿控制器研究［J］.计算技术与自动化，2011，30(1):21-25.KUANG Jianhui，YANG Yimin.Velocity compensate controller of four-wheel drive omni-directional mobile robots based on fuzzy-PD control method［J］.Computing Technology and Automation，2011，30(1):21-25.

［11］LUCAS C，SHAHMIRZADI D，SHEIKHOLESLAMI N.Introducing BELBIC:brain emotional learning based intelligent controller［J］.International Journal of Intelligent Automation and Soft Computing，2004，10(1):11-22.

［12］MEHRABIAN A R，LUCAS C.Emotional learning based intelligent robust adaptive controller for stable uncertain nonlinear systems［J］.International Journal of Computational Intelligence，2005，2(4):1304-4508.

［13］CHEN J P，WANG J B，YANG Y M.A motion control method of four-wheel drive omni-directional mobile robots based on multi points preview control［J］.Journal of Theoretical and Applied Information Technology，2012，45(1):278-284.